樱桃番茄采摘机械手的运动学分析

钟 兴， 张东凤

(1.江苏农林职业技术学院机电工程系，江苏镇江 212400； 2.江苏省现代农业装备工程中心，江苏镇江 212400)

目前，国内樱桃番茄的采摘收获主要靠手工完成。由于收获季节短，劳动力短缺，劳动强度大，大大限制了农场的种植规模。因此，樱桃番茄采摘机械手的研发对现代农业的规模化、多样化、精确化发展有着重要意义[1]。

自1960年开始，国外已开始果蔬收获机械手的研究，由于大多数果蔬需选择性收获，需要较高的科技水平和先进的机器人技术，因此很多产品的性能和成本没有达到商业要求。近年来，高架栽培技术使水果与叶分离，且温室的工作环境比野外好，这为实现机械手采摘收获提供了机会[2]。本研究设计了1种5自由度的关节式樱桃番茄采摘机械手的本体结构，根据Denavit-hartenbery(D-H)法在各关节建立坐标系[3]，推出各个关节及末端执行器的运动学方程；根据末端执行器位姿方程，采用数值法对机械手的工作空间进行求解；对末端执行器运动轨迹进行仿真，验证运动学模型的正确性，以便更好地进行机械手结构优化。

1 机械手运动学分析

1.1 建立运动学模型

樱桃番茄采摘机械手采用关节式结构，由5个连杆在关节处连接构成，共5个自由度，详见图1。旋转座1和小臂4做旋转运动，大臂2、连接臂3和腕关节5做摆动运动，5个关节配合运动，可实现末端执行器6不同的预期运动。

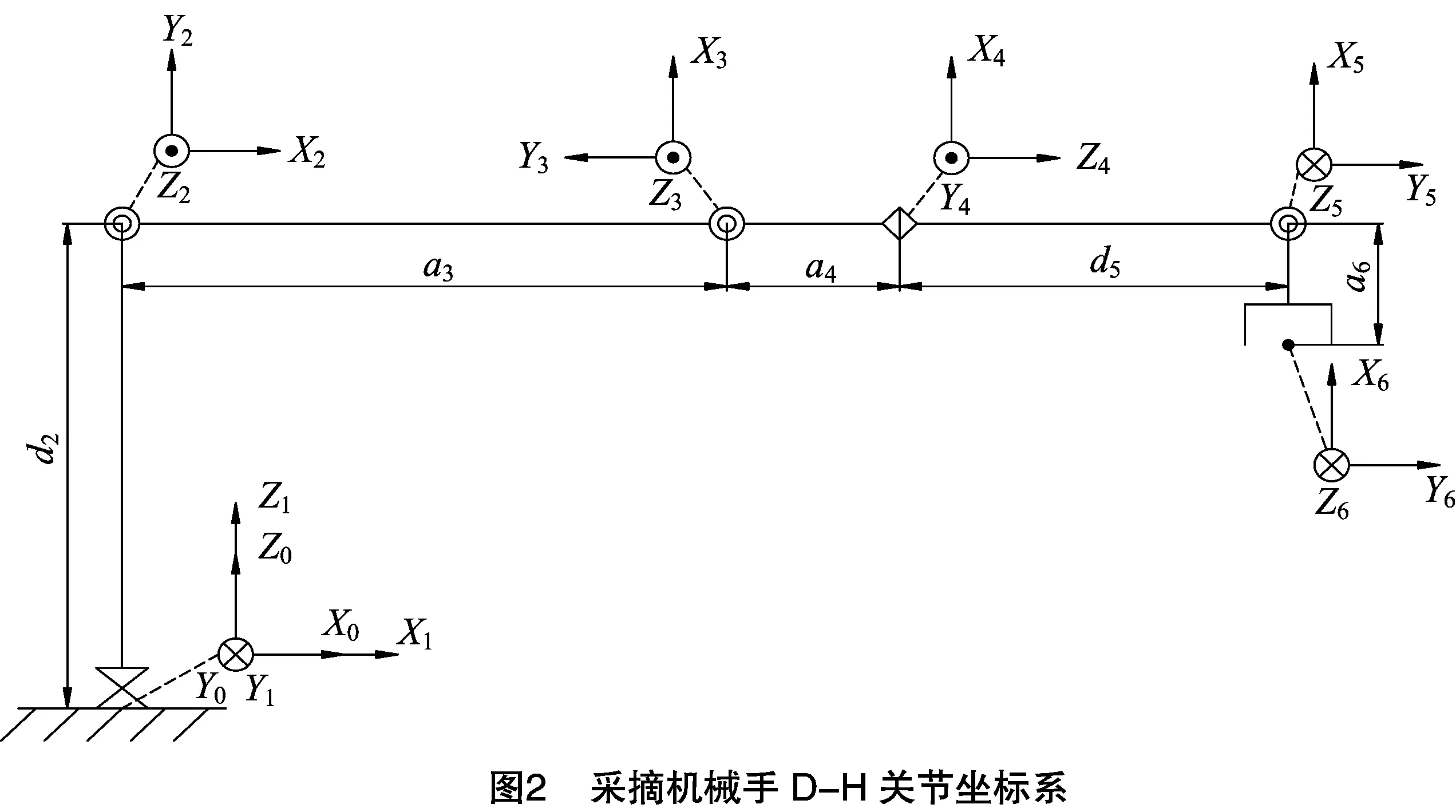
机械手运动学分析是机械手本体结构设计的重要组成部分[4]，本采摘机械手可看作一系列通过转动关节联结起来的连杆，根据D-H法，在机械手各连杆关节和末端执行器建立坐标系(图2)。表1为各连杆和末端执行器的D-H参数，其中，θn是轴xn-1变换到轴xn时绕轴zn的旋转角；dn是轴xn-1和xn之间沿轴zn方向平移的距离；an-1是轴zn-1和zn之间沿轴xn-1方向的平移距离；αn-1是轴zn-1和轴zn共面时绕轴xn-1的旋转角。

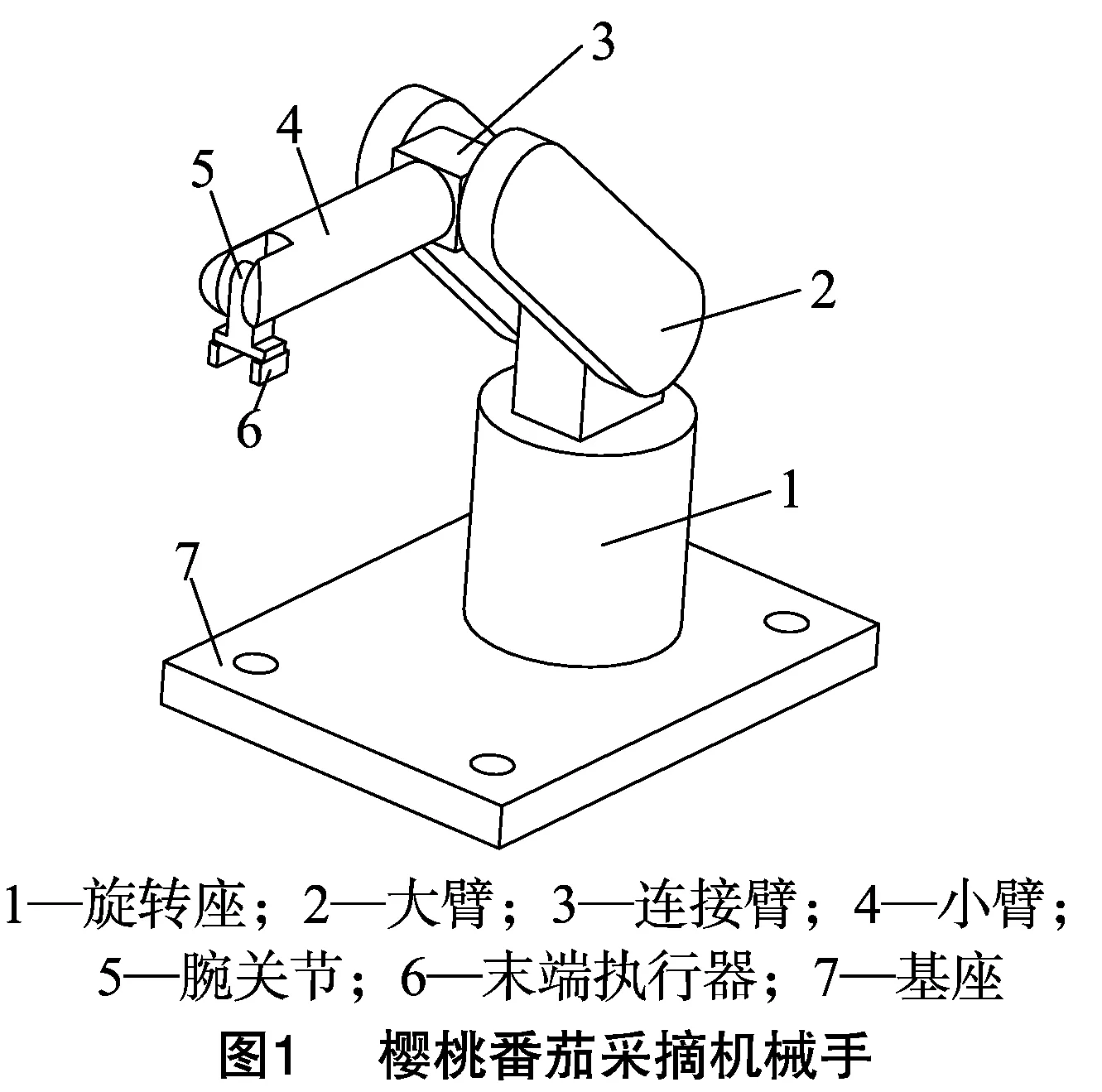
表1 机械手D-H参数

1.2 正运动学求解

机械手的正运动学问题，是指给定1组关节角的值，计算工具坐标系相对于基坐标系的位置和姿态，一般情况下，这个过程被称为从关节空间描述到笛卡儿空间描述的机械手位置表示[3]。

把杆件坐标系固定在该杆件的上关节处，相邻连杆间的转动可以通过矩阵变换加以描述，由坐标系{n}向坐标系{n-1}作变换的齐次变换矩阵：

(1)

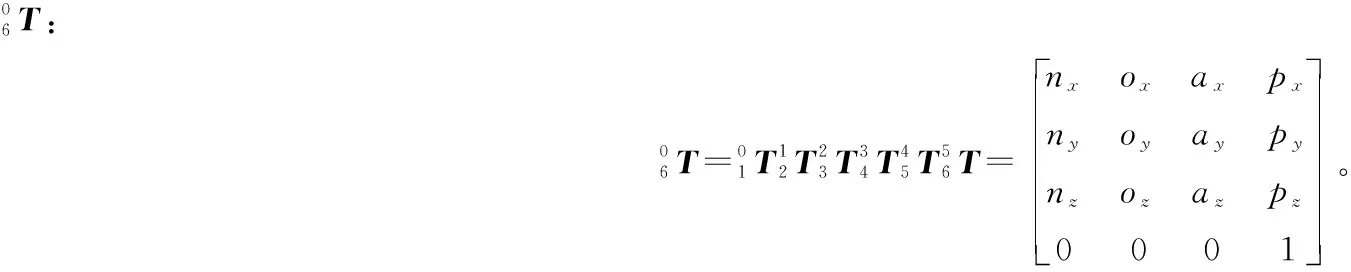
(2)

式(2)中：

nx=c12c34c5+s12s5；

ny=s12c34c5-c12s5；

nz=s34c5；

ox=c12s34；

oy=s12s34；

oz=-c34；

ax=c12c34s5-s12c5；

ay=s12c34s5+c12c5；

az=s34s5；

px=a3c12c3+a4c12c34+d5c12s34+a6(c12c34c5+s12s5)；

py=a3c12c3+a4c12c34+d5c12s34+a6(s12c34c5-c12s5)；

pz=d2-d5c34+a3s3+a4s34+a6s34c5。

计算结果表示的位姿与机械手给定的初始位姿相同，证明运动学方程是正确的。

1.3 逆运动学求解

逆运动学是指给定机械手末端执行器的位置和姿态，计算所有可达给定位姿的关节角，是正运动学的反向求解过程[3]。

由式(2)各元素可得：

θ34=arccosoz；

θ4=θ34-θ3；

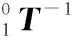
劳动供给者和企业平台之间并不存在传统的“劳动关系”。因而劳动供给者无法享受到劳动者所能享受的权利，例如最低工资、病假、等福利保障。除此之外，工资结算也是零工经济中劳动者经常遇到的难题，劳动价格确立以及劳动量判定所引发的纠纷最为常见，甚至常有拖欠现象出现。基于以上问题，有些人甚至认为这是一种全新的剥削模式[6]。Uber成立之初没有一个全职的员工，并且始终认为无论是全职司机还是兼职司机都是独立的劳动供给者，与Uber之间不存在劳动关系。这降低了Uber运营成本的同时，也降低了劳动者的有效保障。

θ1=θ12-θ2。

由各个关节角的表达式可见，运动学逆解不是唯一的，需根据各关节角的取值范围选取合适的解，以实现最优运动轨迹规划。

2 机械手工作空间求解

具体求解步骤：

(1)由关节变量正运动学方程式(2)得到机械手末端执行器在基坐标系中的坐标值，如式(3)所示。取d2=0.6 m，a3=0.55 m，a4=0.12 m，d5=0.5 m，a6=0.16 m。

(2)关节1和4的角度变化范围为-180°～180°，关节2、3、5的角度变化范围为-170°～170°，关节1转动步距角为80°，其余关节为50°。各关节依次在变化范围内以给定的步距角转动，并且前一关节转动变化后，后面的关节需依次按给定的步距角在自己的变化范围内从最小值转动到最大值，即可得到多组关节变量组合。

(3)

(3)将各组关节变量代入式(3)，求出机械手末端执行器相应位置的向量值。

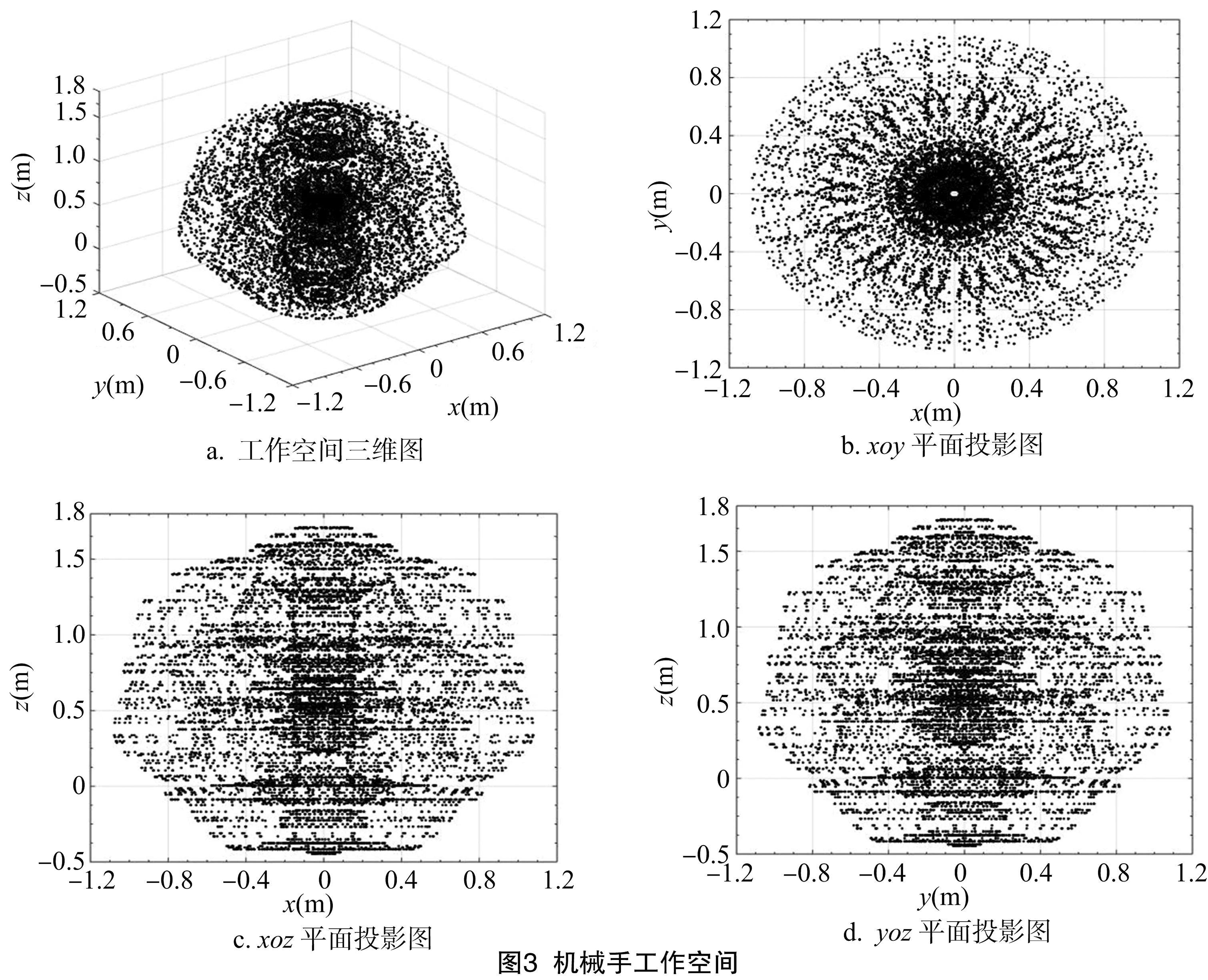
从工作空间x、y、z3个方向的投影及三维图可以看出，该机械手的工作空间连续，没有空腔和空洞，结构紧凑，证明机械手结构设计合理。

3 MATLAB轨迹规划仿真

3.1 建立机械手模型

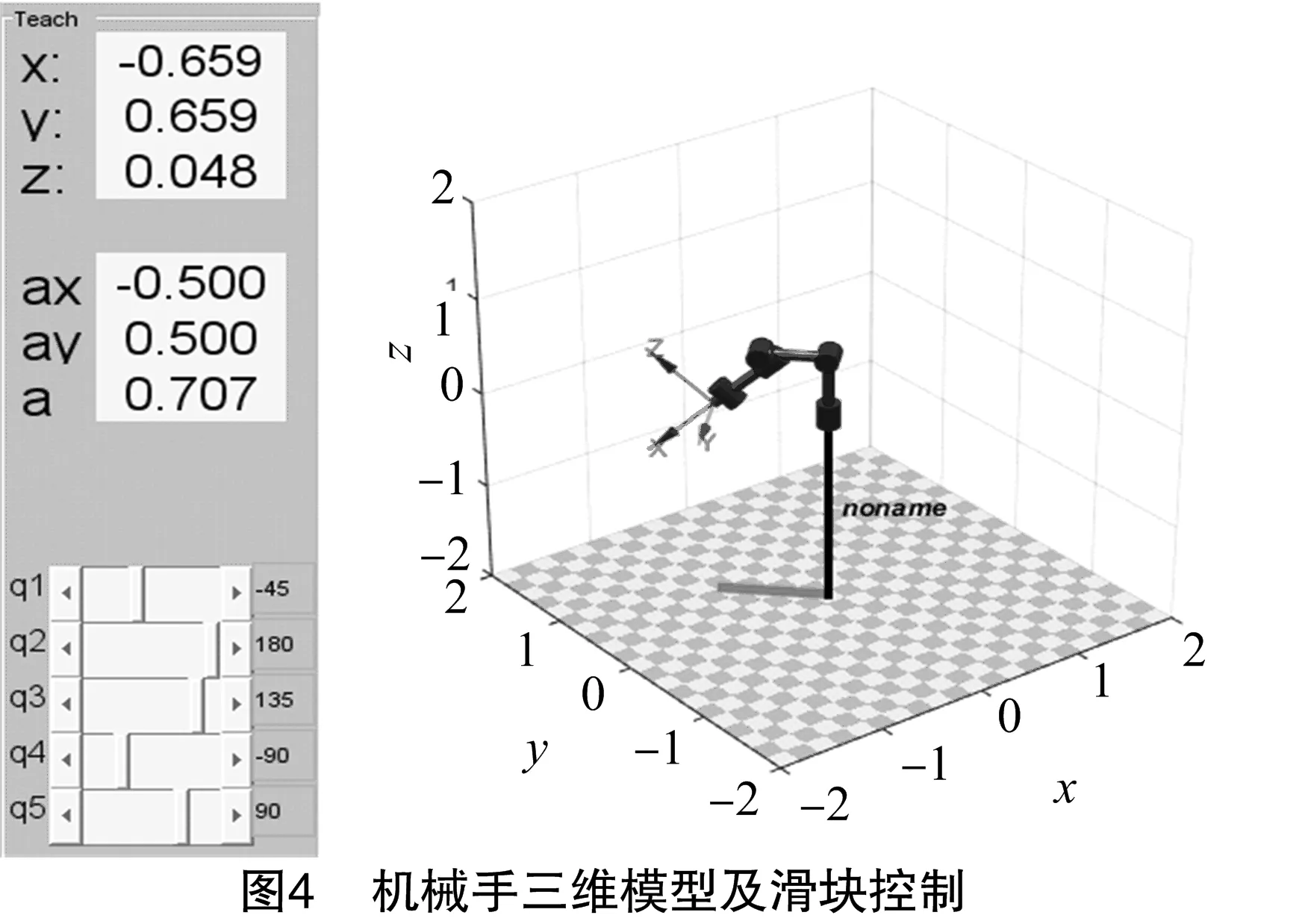
根据表1中机械手各连杆和末端执行器的D-H参数，利用MATLAB机器人工具箱(Robotics Toolbox)中的Link和SerialLink函数，创建机械手三维模型[7](图4)。

3.2 轨迹规划仿真

轨迹指的是机械手每个自由度的位置、速度和加速度的时间历程[8]，给定末端执行器1个目标位姿，轨迹规划仿真将描述机械手在工作空间中的期望运动，在轨迹生成时需计算出各关节和末端执行器的位移、速度和加速度[9]。本例轨迹规划仿真采用点到点的运动规划，主要研究末端执行器和各关节转动角度、速度和加速度变化。

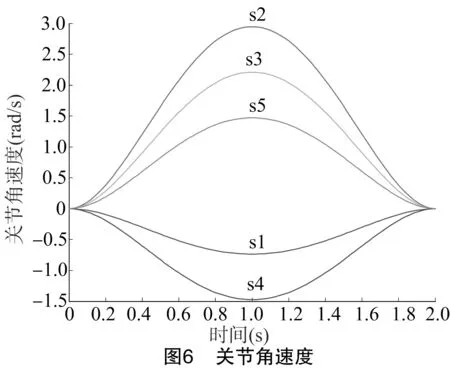
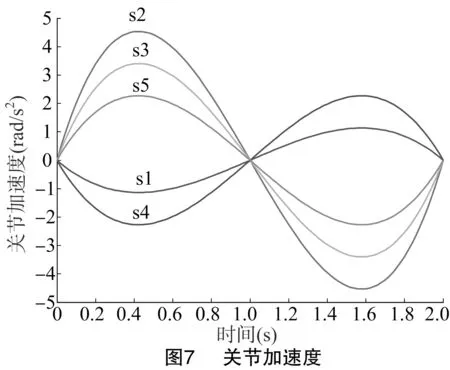
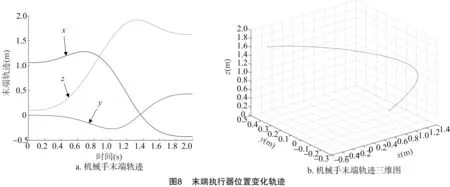
选用起点位置q1=[0 0 0 0 0]，终点位置q2=[-π/4 π 3π/4 -π/2 π/2]，设2点处机械手的初、末速度为零，机械手从q1到q2的时间为2 s， 采用插值算法，插值步长取0.02 s，得到各关节角度变化轨迹[10-11]，如图5所示。对转动角度分别进行一阶和二阶求导运算，即得各关节的速度曲线(图6)和加速度曲线(图7)。采用节点间最简单路径法，可得末端执行器在工作空间的运动轨迹[12]，如图8所示。

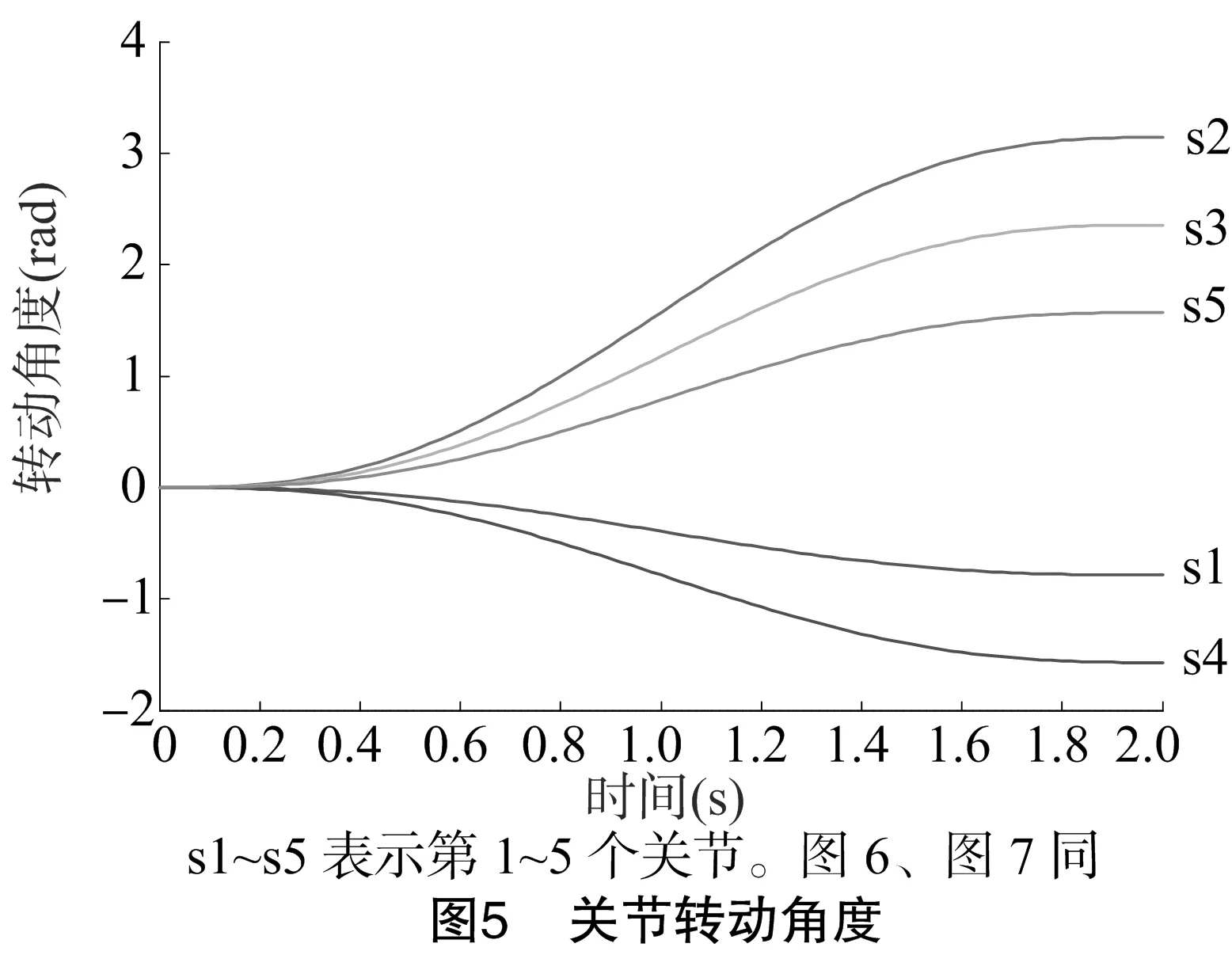
由图5可以看出，关节2角度变化最大，关节1角度变化最小；由图6和图7可以看出，速度和加速度曲线都保持连续平滑，没有突变，说明机械手在工作过程中运行平稳，无较大振动。

4 结论

本研究采用D-H法建立机械手各连杆坐标系，根据各连杆和末端执行器D-H参数建立正、逆运动学数学模型。运用各关节给定步距角转动的方法，结合MATLAB求解出机械手的工作空间，结果显示工作空间连续，没有空腔和空洞。利用MATLAB软件对樱桃番茄采摘机械手进行点到点的运动轨迹仿真，各关节的角度变化曲线、角速度及角加速度曲线均连续平滑，表明机械手运动平稳，安全可靠，可准确到达工作空间内的指定位置，证明机械手结构设计合理，运动学方程正确，为后续的运动控制提供数学模型，也为机械手结构的进一步优化打下基础。

：

[1]蒋昊俣，胡 军，宋 健. 收获采摘机器人的运动学分析及仿真——基于ADMAS[J]. 农机化研究，2016，38(12)：7-11.

[2]Hayashi S，Shigematsu K，Yamamoto S，et al. Evaluation of a strawberry-harvesting robot in a field test[J]. Biosystems Engineering，2010，105(2)：160-171.

[3]Craig J J. Introduction to robotics：mechanics and control[M]. Upper

Saddle River：Pearson Prentice Hall，2005.

[4]张 将，秦训鹏，胡泽启. 一种选择性柔性五自由度机器人的运动学分析[J]. 机床与液压，2016，44(9)：42-47.

[5]陶建国. 机器人技术[M]. 哈尔滨：哈尔滨工业大学出版社，2005.

[6]钟 勇，朱建新. 一种新的机器人工作空间求解方法[J]. 机床与液压，2004(4)：66-67.

[7]郭清达，万传恒，史步海. 基于遗传算法的工业机器人时间最优轨迹规划及仿真研究[J]. 计算机测量与控制，2014，22(4)：1240-1242.

[8]李万莉，陈熙巍，茹 兰. 基于SimMechanics的4自由度机器人的轨迹规划和仿真系统设计[J]. 中国工程机械学报，2008，6(2)：144-148.

[9]刘逸群，邓宗全，刘 振，等. 液压驱动六足机器人一种低冲击运动规划方法[J]. 机械工程学报，2015，51(3)：10-17.

[10]陈 桂，王建红，汤玉东. KUKA机器人运动学仿真与实验研究[J]. 组合机床与自动化加工技术，2014(8)：94-97.

[11]张兴国，张 磊. 禽蛋吸运分级机械仿真与分析[J]. 中国农机化学报，2015，36(5)：157-160.

[12]罗家佳，胡国清. 基于MATLAB的机器人运动仿真研究[J]. 厦门大学学报(自然科学版)，2005，44(5)：640-644.