基于灰色-马尔科夫模型的粮食产量预测

樊 超， 郭亚菲， 曹培格， 杨铁军

(河南工业大学信息科学与工程学院，河南郑州 450001)

粮食是人类赖以生存、社会进步和经济发展的基本生活资料，其产量严重影响着粮食的安全体系，进而关系到能否满足人们的生存需要，它是整个国家安全系统的重要组成部分。因此，粮食产量预测在农业经济管理中起着决定性作用。

通常为了准确预测粮食产量，主要采用以下4类模型：遥感预测模型[1]、气候生产力模型[2]、投入产出模型[3]、多元回归和因子分析模型[4]。这些模型和方法均从不同角度对粮食产量预测进行了研究，并得到一些有意义的研究结果。但是上述模型在预测产量时，存在数据量大、数据处理复杂、考虑影响因素有限等缺点。近年来，随着智能技术的发展，灰色系统理论预测与专家系统相结合的预测、模糊推理预测、人工神经网络预测等新技术避免了传统方法的很多缺陷，被广泛应用。例如，基于粗糙集理论、自回归移动平均模型(ARIMA)、小波变换、神经网络以及组合预测等技术的粮食产量预测方法[5-8]。但是由于粮食生产受到多种因素的影响，导致数据具有较大的波动性和不确定性。从预测结果来看，上述方法均存在一些不足，或者没有考虑粮食生产的灰色性及信息收集的不系统性，或者算法适应性差，预测精度不高。

由于粮食生产具有明显的灰度特征，因此可以使用灰色模型预测粮食产量。传统的灰色模型虽然能有效地预测少量数据的序列，但随着数据的增多和波动性的增大，该模型逐渐失去了它的优势[9]，而马尔科夫模型预测可以应用于随机变化的时间序列中，弥补灰色模型的不足[10]。因此，本研究将上述2种模型相结合，使两者优点互补，充分利用历史数据包含的信息，采用灰色-马尔科夫模型对粮食产量进行短期精准预测。

1 模型建立

1.1 灰色GM(1，1)预测模型

灰色GM(1，1)模型是以微分拟合为核心的一种建模方法，其基本原理是对杂乱无章的原始数据列进行“累加”，生成新的单调递增的数据列，增加原始数据列的规律性，弱化其波动性。按照累加后序列的增长趋势建立预测模型，得到1组单调递增数据。然后对预测数据采用“累减”的方法进行逆运算，恢复原时间序列，得到预测结果。GM(1，1)模型建模步骤如下：(1)设原始时间序列X(0)包含n个非负元素，即

X(0)=[X(0)(1),X(0)(2),…,X(0)(n)]。

(1)

由该序列生成1次累加序列X(1)

X(1)=[X(1)(1),X(1)(2),…,X(1)(n)]。

(2)

(3)

(2)生成累加序列X(1)的紧邻均值序列Z(1)，

Z(1)=[Z(1)(1),Z(1)(2),…,Z(1)(n)]。

(4)

(5)

(3)构建累加序列X(1)的一阶微分方程

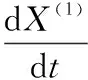
(6)

其中参数a、b可由下式计算

[a,b]T=(BTB)-1BTY。

(7)

(8)

(4)求解微分方程，得到如下GM(1，1)模型

(9)

(5)由累加序列还原原序列

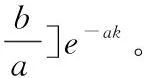
(10)

1.2 马尔科夫模型

马尔科夫方法的基本思路是通过原始数据求得状态转移矩阵，根据状态转移矩阵对未来的变化状态进行概率估计。

马尔科夫模型可表示为

X(n)=X(t)pn-1。

(11)

式中：X(n)、X(t)分别为n、t时刻的状态概率向量，p为1步状态概率转移矩阵。利用马尔科夫模型对灰色模型进行优化时，首先须要对预测精度进行划分，然后确定状态转移概率，最后使用马尔科夫模型对结果进行优化。具体步骤可描述为以下4步。

1.2.1 状态划分 根据灰色模型预测值和真实值的比值将数据样本划分成若干状态，状态个数依据样本数据元素的数量而定。划分的状态可用Ei表示，任一状态可表示为Ei∈[Emin，Emax]，其中Emin和Emax分别是状态Ei的最小值和最大值。

1.2.2 构造转移概率矩阵 该矩阵反映各状态之间的转移规律，可表示为

(12)

式中：pij(k)=mij/mi，表示由状态Ei经过m步转移后到状态Ej的概率。其中mij表示由状态Ei转移到状态Ej的数据个数，mi表示原始数据落入状态Ei的数据个数。通过考察状态转移概率矩阵p(m)，即可预知系统未来的状态转向。

1.2.3 编制预测表 根据上一步得到的状态转移概率矩阵，选取1步或n步转移，编制预测表并将相应转移概率填入表中。然后对预测表的列进行求和，其中最大列所在的状态即为下一步(或n步)最有可能所处的状态。

1.2.4 计算预测值 针对上一步所确定的预测对象最有可能的状态转移Ei以及状态划分规则，计算马尔科夫预测值。

1.3 灰色——马尔科夫预测模型

由于传统的灰色模型主要适用于预测时间短、数据资料少、波动不大的系统对象，对于随机波动性较大的数据序列预测精度较低。而在马尔科夫模型中，通过转移概率可以反映随机因素的影响程度，弥补了灰色预测的局限性，但要求预测序列具有马氏链平稳过程等均值的特点。因此，本研究将灰色预测模型和马尔科夫模型相结合，在提高GM(1，1)模型预测精度的同时，又降低了模型对序列稳定性的要求。算法步骤可描述为：(1)利用灰度建模方法构造粮食产量序列的灰色GM(1，1)模型，并利用该模型得到原序列的预测序列。(2)计算模型预测误差，构造误差预测模型，并利用该模型对产量预测模型进行修正。同时得到修正后第n+1年的预测值。(3)计算原序列和修正预测序列对应元素之间的比值，划分状态区间，得到状态序列，并依据此序列得到新的预测序列，计算序列的自相关系数，进而得到权重序列。(4)将状态序列转化为概率转移矩阵，并根据各阶转移概率密度矩阵和权重系数序列，确定历年状态对预测年所处状态的影响概率。(5)根据状态转移概率及权重系数，计算预测年的粮食产量。将此产量数据加入原数据序列，同时去掉序列中的第1个元素，构成新陈代谢灰度模型，并用基于误差修正的灰度模型预测第n+2年的产量数据。(6)重复步骤(1)～(5)得到第n+3、n+4，…等年份的粮食年产量预测数据。综上，基于灰色-马尔科夫模型的粮食年产量预测算法流程见图1。

2 基于灰色-马尔科夫模型的全国粮食产量预测

为了进一步提高预测精度，本研究对GM(1，1)预测模型的误差进行修正。为此，首先计算预测误差序列E(10)，使用公式(13)进行计算：

E(10)=X10-X10。

(13)

由此得到的误差序列如表1所示。为了对误差序列进行预测，须要将误差序列转化为非负序列。为此，寻找序列E(10)的最小值E(10)min=-2 944，取其绝对值|E(10)min|，将序列E(10)加上该绝对值，从而将误差序列转化为非负序列E(11)，即E(11)=[2 944，4 352，3 729，0，2 756，3 060，3 223，2 415，3 872，2 829，3 086]。

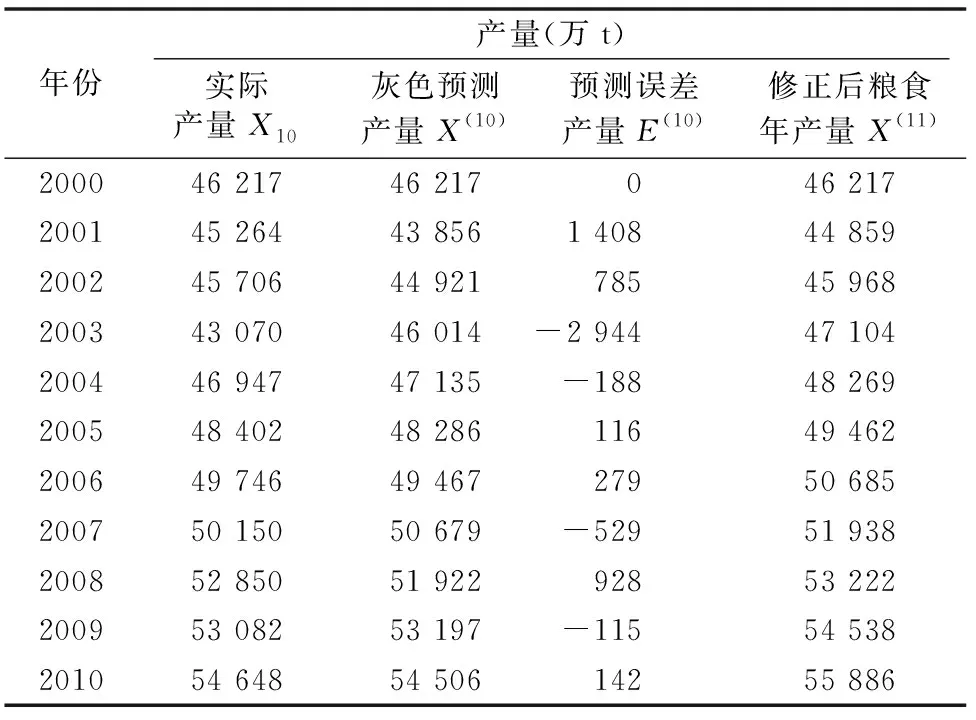
表1 2000—2010年粮食年产量的灰色预测及修正预测值

考虑到粮食生产受到各种因素的影响，而各种因素的影响又具有连续性，本研究使用马尔科夫链描述历年产量对预测年产量的影响。因此，首先计算原序列和预测序列对应元素之间的比值，构成比值序列R，即

(14)

由此得到序列R的最小值Rmin=0.914 36，最大值Rmax=1.009 00，将序列R在Rmin～Rmax内划分成3个区间，即3种状态：区间1(状态1)，[0.91，0.97)；区间2(状态2)，[0.97，0.99)；区间3(状态3)，[0.99，1.01]。

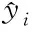
(15)

对X(11)中的所有元素按照上述方法转化为新的预测序列，得到Y1=[46 217，44 859，45 968，44 278，47 304，48 473，49 671，48 822，53 222，53 447，54 768]。同时，根据状态序列S的元素值，得到状态转移频数矩阵F(fij)，元素fij表示状态序列中由状态i转向状态j的频数(即次数)。

(16)

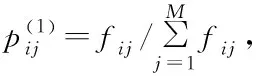
(17)

根据状态转移概率矩阵P(1)，选取距离预测年份(2011年)最近的3个年份，按其距离远近将转移步数分别定为k=1，2，3，即2010年转移步数为1，2009年转移步数为2，2008年转移步数为3。然后计算各阶自相关系数rk，计算公式如下：

(18)

(19)

(20)

式中：n表示预测模型中元素的总个数。

之后对各阶自相关系数进行归一化，得到权重系数序列W，其中元素Wi的计算方法如下：

(21)

(22)

(23)

所以W=[0.536 66，0.359 25，0.104 09]。由于本研究只考虑最近3年对预测年份的影响，因此，可计算每年的转移概率密度矩阵P(2)、P(3)，计算方法见公式(24)、(25)。

(24)

(25)

根据状态矩阵，2008—2010年的粮食年产量状态分别为3、2、2。因此，可分别确定各年份对2011年所处状态的转移概率，具体见表2。

表2 2008—2010年所处状态及状态转移概率

根据表2并利用权重系数序列W计算2011年的粮食年产量分别处于状态1、状态2、状态3的概率分别为

(26)

(27)

(28)

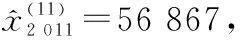
(29)

为对比方便，分别使用传统灰色模型及马尔科夫模型对2011—2015年粮食年产量进行预测，各种方法的预测结果及预测误差见表3。由此可以看出，(1)由于传统灰色模型没有考虑历年粮食产量对未来预测年份粮食产量的影响，初始预测值较为准确，2011—2013年的预测误差小于1.00%，但随着年份的增加，由于粮食年产量间的相互影响作用导致预测精度变差，2014、2015年的年产量预测误差明显增加，但总体来看，此方法的预测精度较高；(2)传统马尔科夫模型由于过度依赖历年粮食产量对未来产量的影响，降低了序列的波动性，导致预测值增加较慢，预测误差较大，所有年份的预测误差均大于1.50%，最大误差达到4.16%，无法用于粮食产量的短期精准预测；(3)相比于传统灰色模型和马尔科夫模型，由于灰色——马尔科夫混合模型综合考虑了序列的波动性及历年产量对未来年份粮食产量的影响，将2种模型优势互补，极大地提高了模型预测的准确性，5年的粮食产量误差均小于 0.40%，能够实现粮食产量的短期精准预测。

表3 各种方法粮食产量预测结果比较

3 结论

粮食安全问题是关系国民经济健康发展和全面建设小康社会的重大问题，因此研究粮食生产波动规律，做好粮食产量的短期预测对保障国家粮食安全和协助粮食管理部门作出科学决策具有重大意义。本研究结合粮食生产具有波动性及相互影响性的特点，提出基于马尔科夫的灰色产量组合预测方法，该方法充分发挥了灰色模型和马尔科夫模型的优势，利用历史数据包含的信息，对粮食年产量进行短期精准预测，5年预测误差均小于0.40%，平均误差为0.19%，相较于传统灰色模型及马尔科夫模型，预测精度大幅提高。

：

[1]李卫国，王纪华，赵春江，等. 基于遥感信息和产量形成过程的小麦估产模型[J]. 麦类作物学报，2007，27(5)：904-907.

[2]王桂芝，胡 慧，陈纪波，等. 基于BP滤波的Fourier模型在粮食产量预测中的应用[J]. 中国农业气象，2015，36(4)：472-478.

[3]陈锡康，杨翠红. 投入占用产出技术在全国粮食产量预测及乡镇企业中的应用[J]. 中国科学基金，2003，17(3)：149-152.

[4]王春辉，周生路，吴绍华，等. 基于多元线性回归模型和灰色关联分析的江苏省粮食产量预测[J]. 南京师大学报(自然科学版)，2014，37(4)：105-109.

[5]林 芳. 灰色神经网络在粮食产量预测中的应用[J]. 计算机仿真，2012(4)：225-228.

[6]王惠婷. 基于混合时间序列模型的粮食产量预测[J]. 统计与决策，2013(12)：23-25.

[7]陈 晨，吴海云，田燕红，等. 基于支持向量回归机的粮食产量预测研究[J]. 山西农业大学学报(自然科学版)，2013，33(4)：357-361.

[8]杨铁军，杨 娜，朱春华，等. 一种新的基于ARIMA模型的粮食产量预测[J]. 河南工业大学学报(自然科学版)，2015，36(5)：19-22.

[9]杨克磊，张振宇，和 美. 应用灰色GM(1，1)模型的粮食产量预测研究[J]. 重庆理工大学学报(自然科学版)，2015，29(4)：124-127.

[10]邹 慧，徐 波. 改进的灰色——马尔科夫模型及其在沉降预测中的应用研究[J]. 工程勘察，2016，44(3)：64-68.