固液两相流粒子冲蚀钻头内流道磨损

赵健，张贵才，徐依吉，王瑞和，周卫东，韩烈祥



固液两相流粒子冲蚀钻头内流道磨损

赵健1, 2，张贵才1, 2，徐依吉1，王瑞和1，周卫东1，韩烈祥3

(1. 中国石油大学(华东) 石油工程学院，山东 青岛，266580；2. 中国石油大学(华东) 科学技术研究院，山东 东营，257061；3. 中国石油集团川庆钻探工程有限公司钻采工程技术研究院，四川 德阳，618300)

针对固液两相流粒子冲蚀钻头内流道磨损机制，应用固液两相流离散相模型(discrete phase model，DPM)，建立钻头内流道冲蚀磨损的物理模型，获得粒子参数对内流道磨损的影响规律，并进行室内实验，验证DPM模型的有效性。研究结果表明：粒子对钻头内流道冲蚀磨损主要分布在内流道收缩面，越靠近钻头中心轴线，磨损率越大；随粒子入口速度的增大，内流道平均磨损率增大；随粒子直径的增大，内流道平均磨损率先减小后增大，最后趋于稳定，当直径为2.0 mm时平均磨损率最小；随粒子体积分数的增大，内流道平均磨损率近似呈直线增加；当粒子入口角度为50°时，内流道平均磨损率最大；压力对于内流道磨损影响较小；进行100 h磨损实验后，钻头内流道的磨损率减小了0.80%。

固液两相流；内流道磨损；离散相模型；粒子参数；钻头

粒子冲击钻井技术通过在钻井液中加入体积分数为1%~5%、直径为0.5~5.0 mm的钢质粒子，钢质粒子和钻井液混合后，通过井下钻头喷嘴高频和高速喷出破碎岩石，实现了粒子冲击和钻头机械联合破岩，改变了常规钻头的破岩方式，极大提高了钻头破岩效率，但钢质粒子的加入会加大钻头内流道的冲蚀磨 损[1−7]。固液两相流冲蚀磨损是常见的材料磨损形式，该研究方向已取得较大进展，粒子冲击速度对材料的冲蚀磨损率影响较大，冲蚀磨损率可用冲击速度的幂函数表示[8−10]。WANG等[11−13]分析单粒子冲击白口铸铁过程，建立粒子参数与破碎坑体积关系的数学模型，通过建立的固体颗粒冲击磨损模型，应用转换系数确定磨损类型。HASHISH[14]应用高速摄影技术分析磨料射流切割透明材料过程，表明冲击角度会影响材料磨损类型。弯管冲蚀磨损中直径300 μm磨料的冲蚀磨损率比直径150 μm磨料的冲蚀磨损率高[15]。HADAVI 等[16−17]研究表明约87%粒子冲击动能消耗在粒子冲击磨损过程。MOMBER[12]发现当粒子冲击速度较大时，材料磨损率和材料特性存在较好的拟合关系。NSOESIE等[18−21]发现当粒子冲击合金时存在能够改变合金磨损速率的临界冲击角度，弯管角度对液固流化床内压力速度分布有较大影响。直角弯管在90°转角和下游水平管路中存在流动分离现象。董刚等[22−23]研究表明磨料形状是影响材料冲蚀率的重要因素，改变固体颗粒直径对叶片磨损的影响最大，对质量流量的影响次之。钝角磨料(石英砂)的主要冲蚀机制是缺陷部断裂和基质切削，尖角磨料(碳化硅)的主要冲蚀机制是骨料断裂和基质犁削[24]。铸钢、Cr20和Cr26白口铸铁冲蚀产生最大蚀磨损率的冲蚀角度均为45°[25]。大粒径颗粒在叶片头部发生大角度冲击之后，会在叶片中后段再次发生小角度2次冲击[26]。在高雷诺数下，颗粒无规则运动程度从中心到壁面呈现先增强后减弱的趋势[27]。单位长度钻杆磨损量随冲蚀时间增加而逐渐增大[28]。通过以上分析可知粒子的速度、直径、角度等参数对冲蚀磨损的影响较大，为本文研究粒子对钻头内流道冲蚀提供了指导和借鉴，但以上研究基本为纯水或金刚石、石英砂、石榴石等磨料的冲蚀磨损，而大直径球形钢质粒子对钻头内流道的冲蚀磨损研究较少，同时，前期冲蚀磨损的研究条件与实际钻井现场差距较大，因此得出的结论有限制。本文作者应用固液两相流离散相(discrete phase model，DPM)模型，获得粒子参数对钻头内流道冲蚀磨损的影响规律，并进行室内实验验证，模拟和实验条件均符合钻井现场条件，研究结果可为粒子冲击钻头的设计与应用提供参考。

1 数值模型

粒子与钻井液形成的固液两相流会对钻头内流道产生冲蚀磨损，应用固液两相流离散相(DPM)模型，通过Fluent软件求解[29−31]，将钻井液假设为连续流动介质，粒子为离散、不连续的固体颗粒介质，即钻井液为连续相，粒子为分散相，对连续相求解采用Euler方法，对分散相描述则采用Lagrange方法。

1.1 控制方程

定义液相为不可压缩流体，其流动方程用连续性方程和N−S方程表示[29−31]：

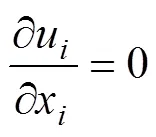
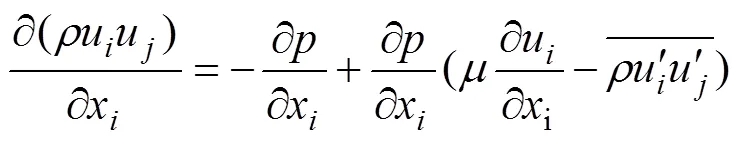
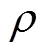
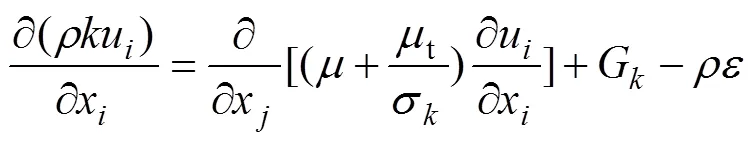
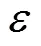
1.2 离散相模型及磨损方程

通过分散相粒子运动方程计算其运动轨迹，粒子运动方程为[17, 30, 32]

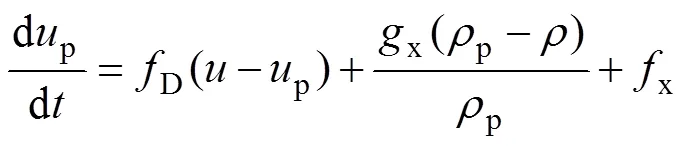
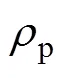
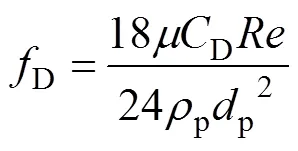
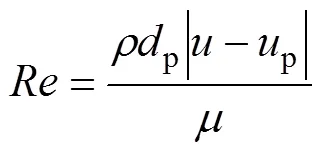
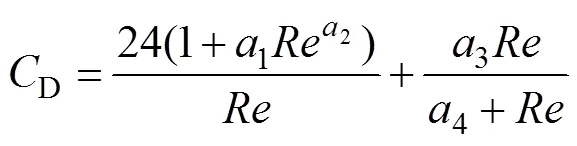
Fluent磨损计算模型，冲蚀磨损公式[17, 30]为

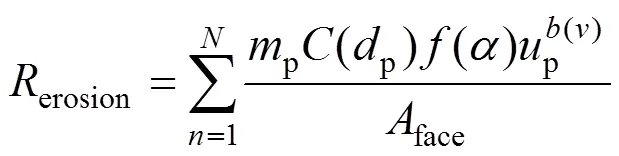
1.3 几何建模及条件设置

将建立的物理模型导入Gambit软件中完成网格划分，如图1(b)所示。定义模拟环境和各项参数，粒子密度为7.8 g/cm3，水力直径为0.08 m，入射粒子速度指数设为2.4，直径函数值为1.8×10−9，模拟固液两相流粒子冲蚀钻头内流道的磨损特性。

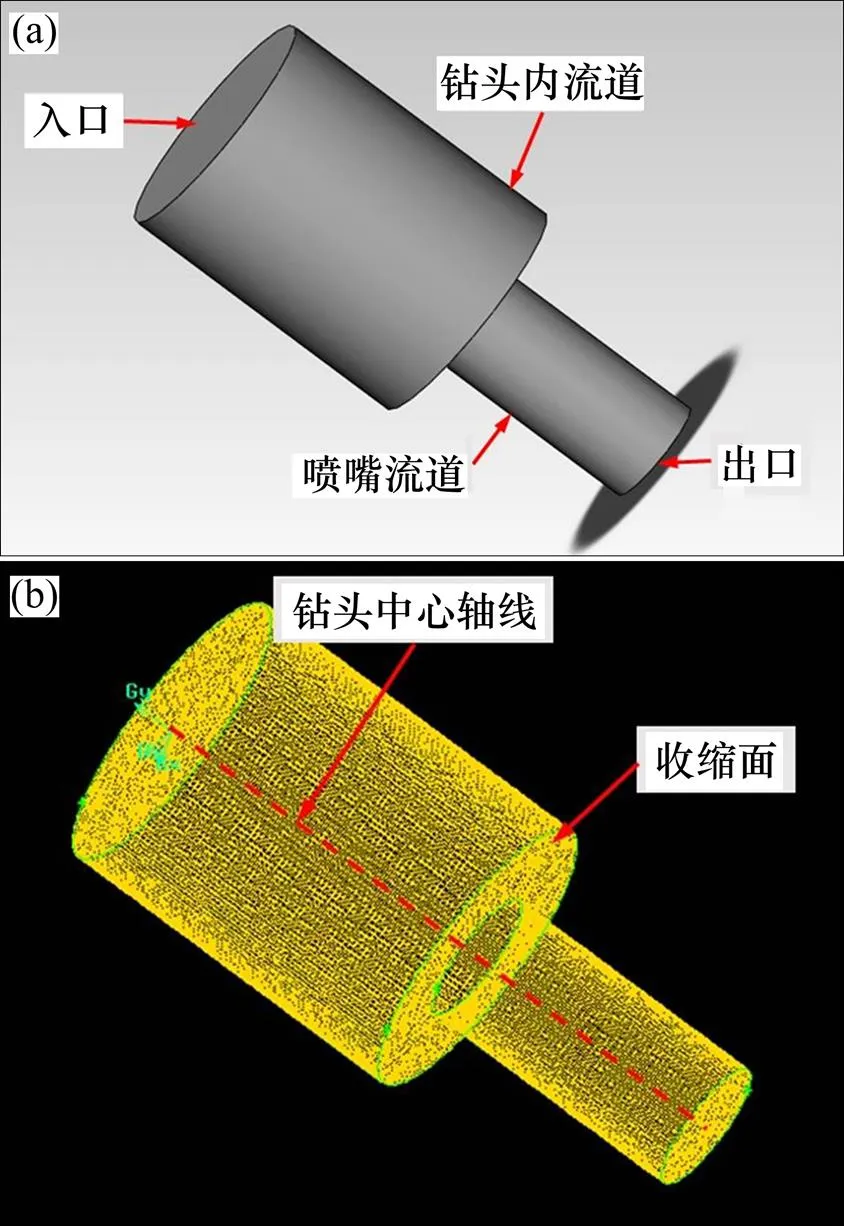
(a) 物理模型；(b) 网格划分

2 模拟结果分析

2.1 粒子运动轨迹

当粒子速度为10 m/s、直径为2.0 mm、体积分数为5%时，钻头内流道内粒子运动轨迹如图2所示。由图2可见：0 s时粒子进入钻头内流道，0.025 s时粒子达到内流道收缩面，部分粒子开始撞击收缩面并反弹，反弹粒子在流体流动阻力作用下速度降为0 m/s后，开始继续沿着流体运动方向流动，最终被流体携带至喷嘴流道内。因此，粒子到达钻头内流道收缩面后会分成2部分，其中，一部分直接进入喷嘴流道，另一部分需要经过不断反弹后进入喷嘴流道。

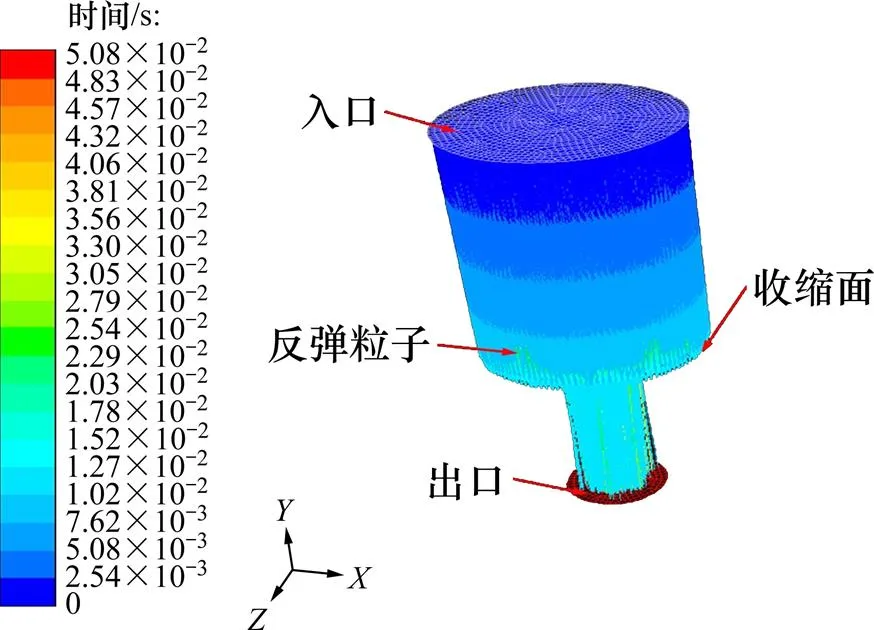
图2 钻头内流道粒子运动轨迹

2.2 内流道冲蚀磨损

当粒子速度为10 m/s、直径为2.0 mm、体积分数为5%时，钻头内流道冲蚀磨损如图3所示。由图3可见：粒子对内流道冲蚀磨损主要分布在内流道收缩面，越靠近钻头中心轴线，磨损率越大，内流道收缩面与喷嘴流道连接处冲蚀磨损率最大。其原因主要有2个方面：一方面，从碰撞次数方面分析，越靠近收缩面中心，粒子碰撞收缩面的次数越多，因此，磨损越严重；另一方面，从冲击速度方面分析，越靠近钻头中心轴线，粒子和流体的运动速度越大，撞击壁面的速度越大，因此，冲蚀磨损率越大。

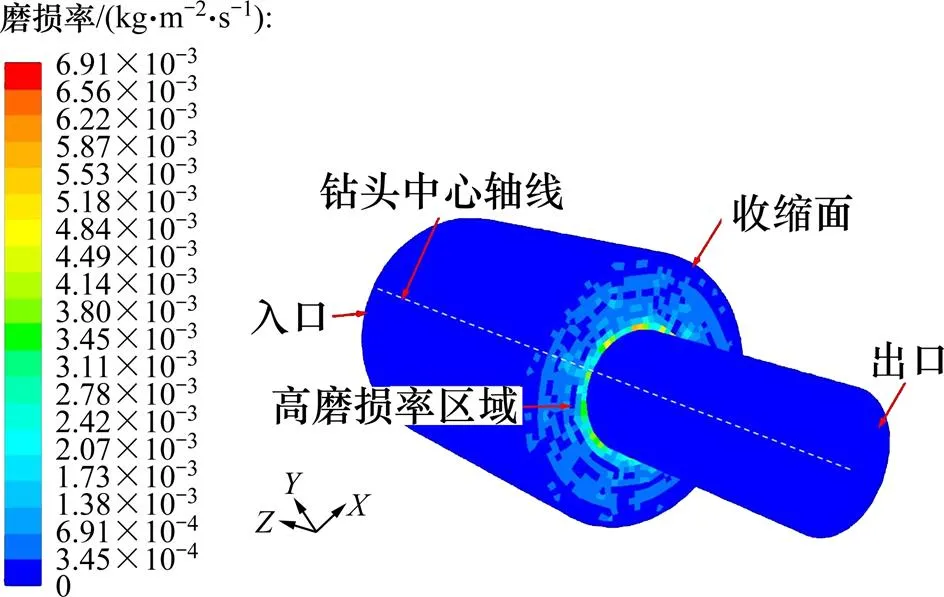
图3 钻头内流道冲蚀磨损情况

方向冲蚀磨损投影如图4所示。从图4可见：沿着方向(内流道收缩面的径向方向)，从壁面到钻头中心轴线冲蚀磨损率逐渐增大；当为−40~−20 mm和20~40 mm时，从内流道壁面到钻头中心轴线，磨损率缓慢增大；当为−20~20 mm时，冲蚀磨损率迅速增大。

2.3 入口速度的影响

当粒子直径为2.0 mm、体积分数为5%、入口角度为0°时，入口速度对钻头内流道冲蚀磨损的影响如图5所示。由图5可见：随着入口速度增大，内流道的平均磨损率和最大磨损率均增大，当入口速度大于10 m/s时，2种磨损率迅速增加；随着入口速度增大，粒子动能迅速增加，对内流道表面的冲击力不断增大，冲蚀磨损更加严重，因此，磨损率不断增加。在现场应用时，可适当增大内流道入口直径来降低粒子入口速度，从而减少钻头对内流道的冲蚀磨损。

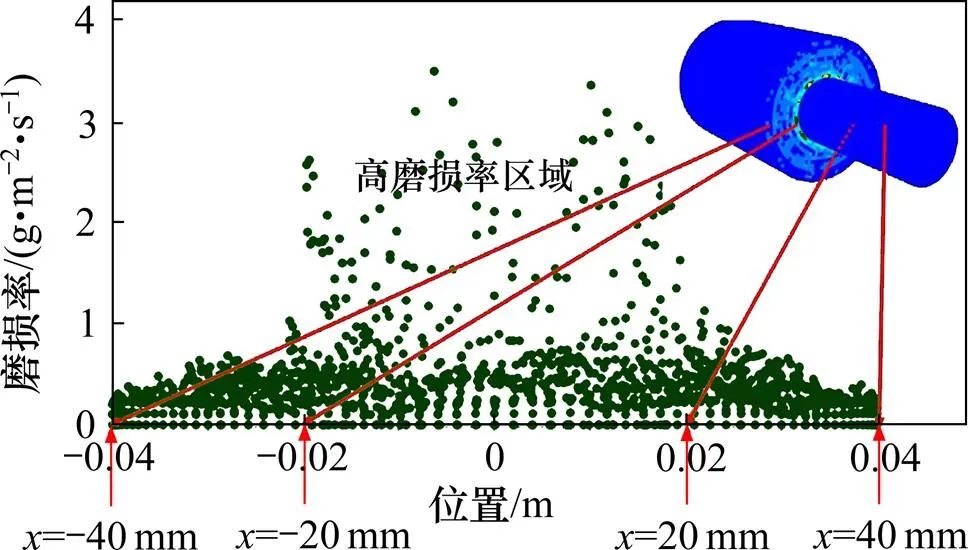
图4 x方向内流道磨损投影

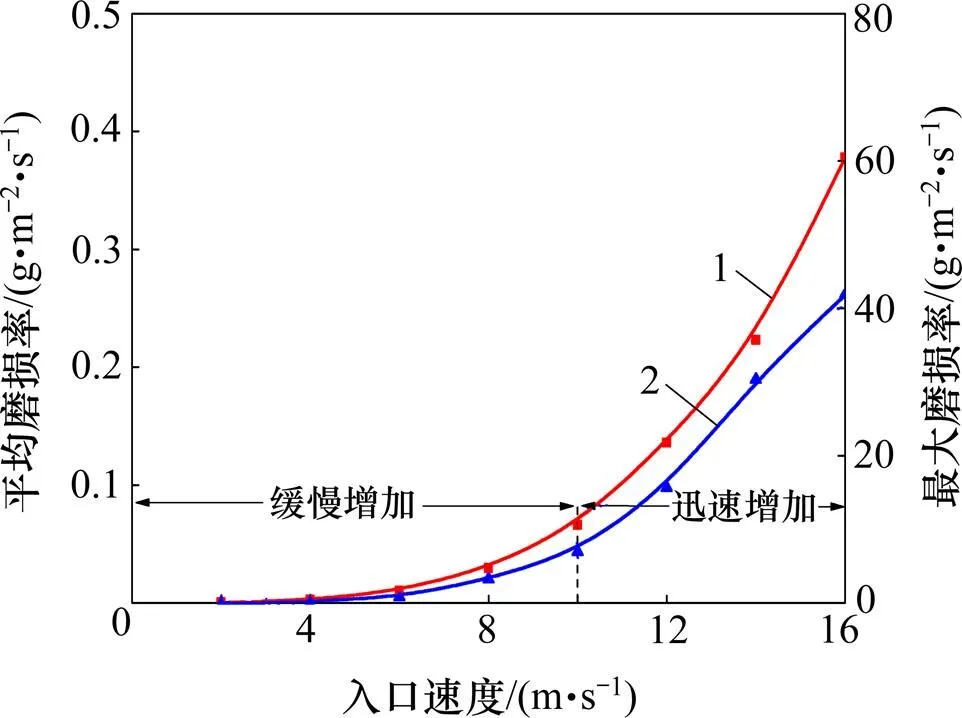
1—平均磨损率；2—最大磨损率。

2.4 粒子直径影响

不同粒子直径的钻头内流道磨损情况如图6所示。从图6可见：5.0 mm粒子冲蚀内流道磨损范围比0.5 mm粒子冲蚀磨损范围大；虽然0.5 mm粒子冲蚀磨损范围小，但冲蚀磨损率比5.0 mm的大。

当入口速度为10 m/s、体积分数为5%、入口角度0°时，粒子直径对钻头内流道冲蚀磨损的影响如图7所示。由图7可见：随着粒子直径不断增大，内流道平均磨损率先减小后增大，最后基本不变。在相同粒子体积分数下，粒子直径的增大会导致粒子总数量减少，从而减少冲击内流道壁面的粒子数量，同时直径增大会增大冲蚀磨损区域(图6)，数量减少和冲蚀区域增大，都会降低钻头内流道磨损率。但直径增大会增加粒子对壁面的冲击力，从而增大磨损。当粒子直径小于2.0 mm时，冲击数量减小和冲蚀区域减小作用起主导作用，因此，粒子冲蚀磨损率逐渐减小。但随着粒子直径继续增大，冲击力的增大起主导作用，因此，粒子冲蚀磨损率会增大。当粒子直径大于3.0 mm后，2方面原因相互制约达到稳定，冲蚀磨损率基本不变。所以，从减少冲蚀磨损方面考虑，最优的粒子直径为2.0 mm。随着粒子直径增大，最大磨损率逐渐减小。在相同体积分数下，粒子直径增加，数量减少，且直径越大，冲蚀磨损范围越大(图6)，所以，粒子对内流道壁面同一位置的冲蚀磨损率变小，粒子直径增大，最大磨损率逐渐减小。

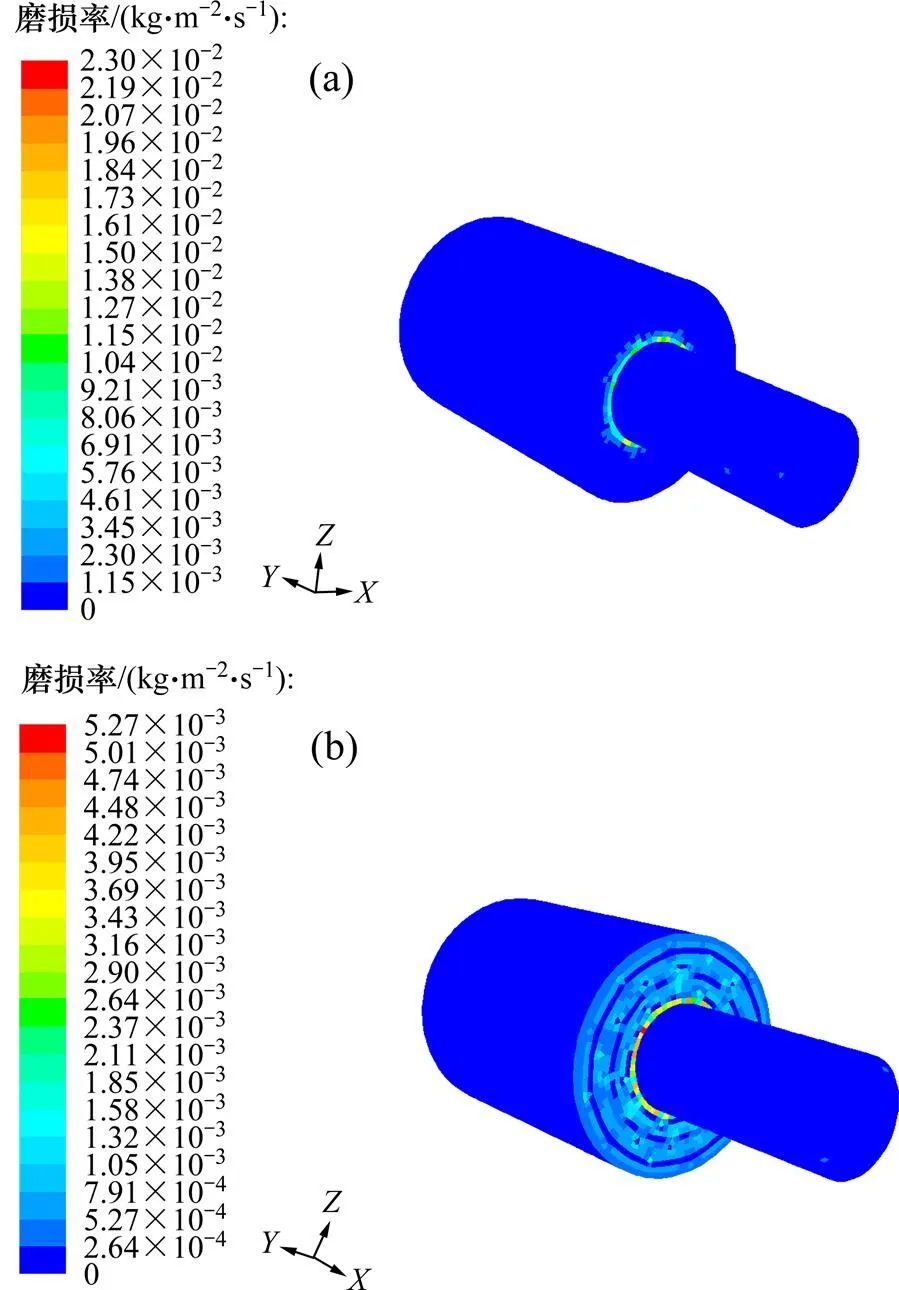
(a) 0.5 mm；(b) 5.0 mm

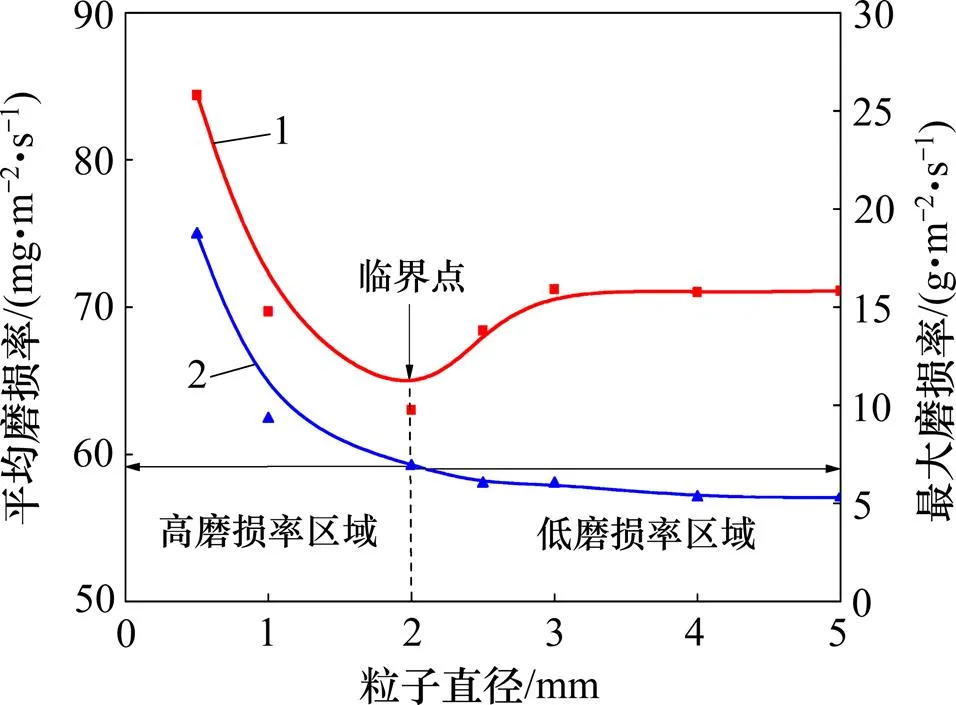
1—平均磨损率；2—最大磨损率。

2.5 粒子体积分数影响

当粒子直径为2.0 mm、入口速度为10 m/s、入口角度为0°时，粒子体积分数对钻头内流道冲蚀磨损的影响如图8所示。由图8可见：随粒子体积分数增大，内流道平均磨损率近似呈直线增加。粒子体积分数增大导致同等体积下粒子数量增多，因此，单位时间内撞击内流道次数增多；体积分数增大后，粒子间会相互碰撞，增加了碰撞次数以及碰撞范围，因此，体积分数增大会增大内流道的平均磨损率。随粒子体积分数不断增大，最大磨损率先增大，后趋于平缓。粒子体积分数增大后，粒子冲蚀内流道同一区域次数增加，因此，最大磨损率不断增大。当粒子体积分数大于5%后，粒子之间碰撞干扰加剧，撞击内流道壁面同一位置的粒子会发生相互干扰，影响壁面同一位置的磨损率，因此，当粒子体积分数大于5%后，最大磨损率趋于平缓。

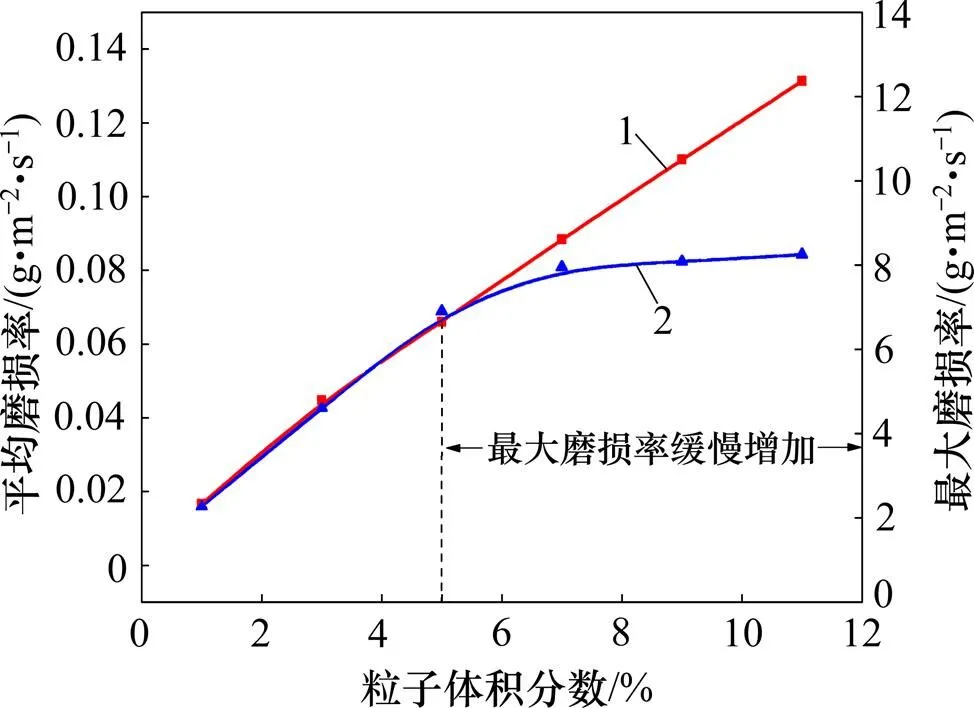
1—平均磨损率；2—最大磨损率。

2.6 入口角度的影响

当粒子体积分数为5%、直径为2.0 mm、入口速度为10 m/s时，入口角度对钻头内流道冲蚀磨损的影响如图9所示(入口角度为粒子流入方向和钻头中心轴线的夹角)。由图9可知：随入口角度不断增加，平均磨损率先增大后减小，当入口角度为50°时，平均磨损率最大。随入口角度的增大，粒子以倾斜方式冲击内流道壁面，运动轨迹越来越紊乱，反弹粒子数量逐渐增多，粒子和壁面碰撞次数不断增加，因此，平均磨损率先不断增大，当入口角度为50°时，粒子运动轨迹最紊乱，粒子轨迹呈现“漩涡”状，此时，粒子撞击内流道壁面的次数最多，因此，平均磨损率最大。随入口角度继续增大，粒子流动轨迹逐渐规则，撞击内流道壁面的次数开始减少，因此，当入口角度大于50°后，平均磨损率开始减小。随粒子入口角度增大，最大磨损率先增大后减小，当入口角度为20°时，最大磨损率达最大值。随入口角度增大，内流道收缩面处冲蚀磨损区域开始逐渐聚集，磨损区域开始减小，单位面积上粒子撞击的数量增大，因此，最大磨损率开始增大。当入口角度为20°时，最大磨损率达到最大值；入口角度继续增大，部分粒子不经过收缩面，而从壁面直接反弹，对收缩段磨损减小，因此，最大磨损率开始减小。

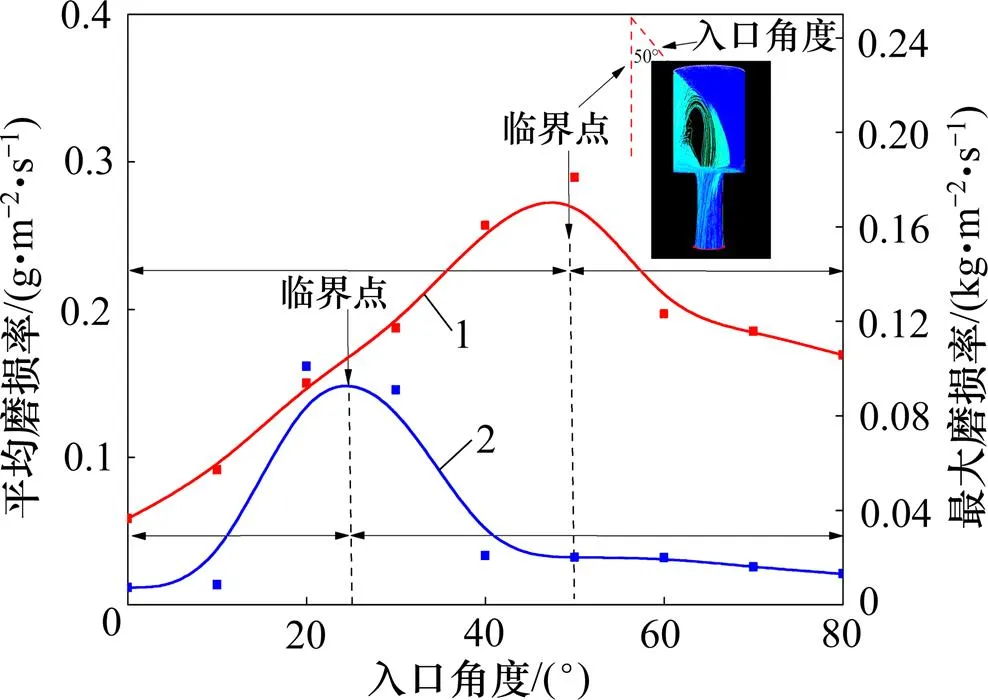
1—平均磨损率；2—最大磨损率。

2.7 压力影响分析

当入口角度为0°、速度为10 m/s、直径为2.0 mm时，压力对钻头内流道冲蚀磨损的影响如图10 所示。由图10可知：随着压力不断增大，平均磨损率和最大磨损率基本不变，说明压力对内流道的磨损影响较小。在其他条件不变，改变内流道压力时，虽然系统压力升高，但较稳定，粒子运动轨迹没有较大变化，因此，压力对内流道平均磨损率和最大磨损率的影响均较小。

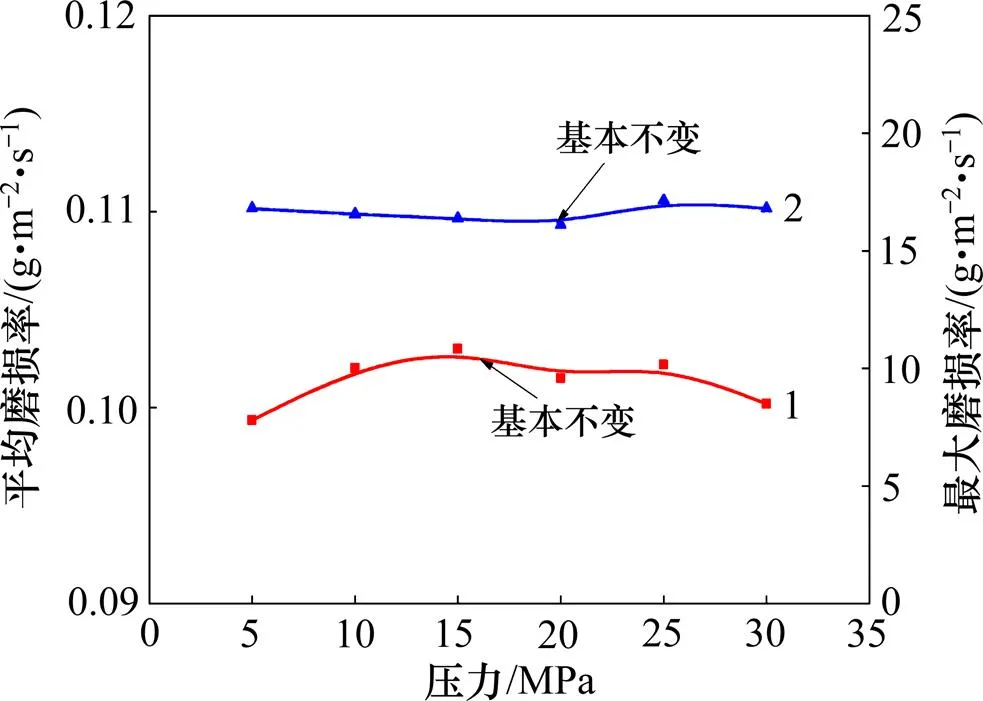
1—平均磨损率；2—最大磨损率。

3 冲蚀磨损实验

3.1 实验设备

粒子冲蚀钻头内流道实验装置主要包括磁选机、旋转储罐、射流混浆器、钻头钢套、循环管线、泥浆罐、振动筛、砂泵等。粒子经过射流混浆器注入，与钻井液混合，粒子在钻井液携带下冲蚀钻头内流道后，经过磁选机将粒子分离，分离后的粒子储存到旋转储罐中，旋转储罐再将储存的粒子输送至射流混浆器中，粒子不断循环对钻头内流道造成持续冲蚀(钻头安装在钻头钢套内)，实验装置如图11所示。

图11 磨损实验装置实物图

钻头内流道冲蚀磨损实验共进行100 h。实验进行50 h后，增加泵压、排量，继续进行50 h，实验参数如表1所示。

表1 实验参数

注：钻井液漏斗黏度指钻井液通过马氏漏斗的时间。

3.2 结果分析

100 h钻头内流道冲蚀磨损结果如图12所示。由图12可知：实验的后50 h，即排量增大后，粒子入口速度增大，因此，磨损率高于前50 h的磨损率，数值模拟结果与实验结果基本吻合，验证了DPM模型的有效性。实验50 h时钻头内流道磨损率减小了0.19%，100 h时钻头内流道磨损率减小了0.80%，磨损不 严重。

实验完钻头内流道磨损如图13所示。由图13可知：内流道冲蚀磨损主要集中在收缩面，验证了数值模拟结果，虽然收缩面处存在一定磨损，但冲蚀并不严重。实验钻井液排量与钻井现场液排量一致。

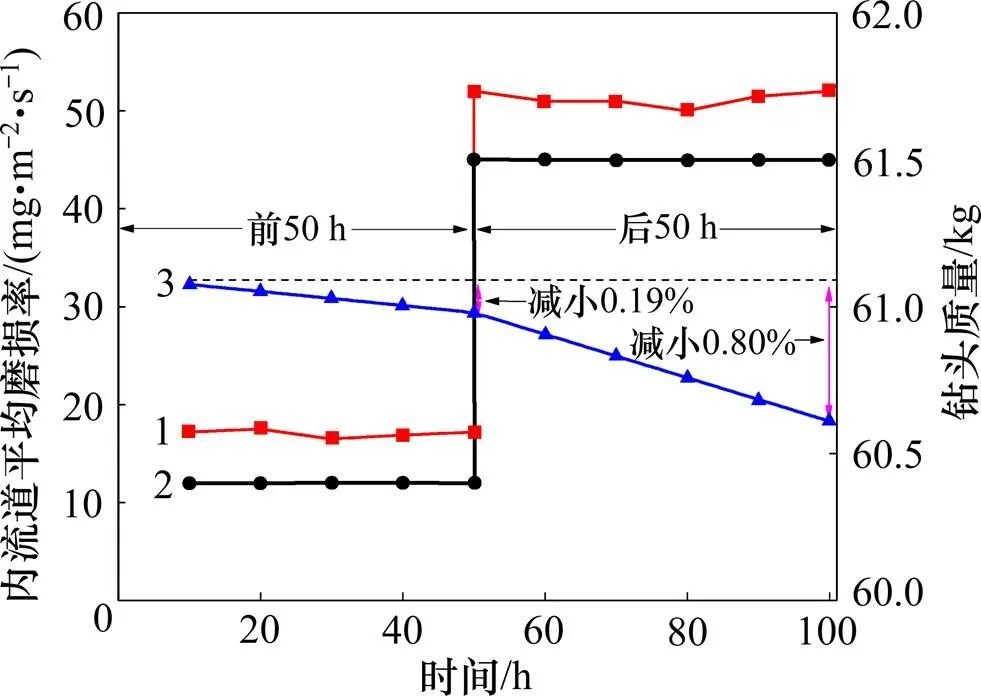
1—实验平均磨损率；2—模拟平均磨损率；3—钻头质量。

(a) 钻头内流道；(b) 内流道收缩

4 结论

1) 粒子达到钻头内流道收缩面后会分成2部分：一部分直接进入喷嘴流道，另一部分需要经过不断反弹后进入喷嘴流道。粒子对内流道冲蚀磨损主要分布在内流道收缩面，越靠近钻头中心轴线，磨损率越大，收缩面与喷嘴流道连接处磨损率最大。

2) 随入口速度增大，内流道平均磨损率和最大磨损率均增大。当入口速度大于10 m/s时，这2种磨损率迅速增加，现场应用时可适当增大内流道入口直径以降低粒子入口速度，从而减少磨损。随着粒子直径不断增大，内流道平均磨损率先减小后增大，最后基本不变。当粒子直径为2.0 mm时，平均磨损率最小，随粒子直径增大，最大磨损率逐渐减小。

3) 随着粒子体积分数增大，内流道平均磨损率近似呈直线增加，当体积分数大于5%后，最大磨损率趋于平缓；随入口角度不断增加，平均磨损率先增大后减小。当入口角度为50°时，平均磨损率最大，随粒子入口角度增大，最大磨损率先增大后减小；当入口角度为20°时，最大磨损率最大；压力对内流道平均磨损率和最大磨损率的影响较小。

4) 进行50 h实验后钻头内流道磨损量率减小了0.19%，进行100 h实验后钻头内流道磨损率减小了0.80%，数值模拟结果与实验结果基本吻合，验证了DPM模型的有效性。钻头内流道冲蚀磨损主要在收缩面，虽然内流道存在一定磨损，但不严重。

[1] TIBBTITTS G A, GALLOWAY G G. Particle drilling alters standard rock-cutting approach[J]. World Oil, 2008, 229(6): 37−44.

[2] TIBBTITTS G A, GALLOWAY G G, TERRY J B. Impactor excavation system having a drill bit discharging in a cross over pattern: US8845279B2[P]. 2013−07−16.

[3] GALLOWAY G G. Shot blocking using drilling mud: US8342256B2[P]. 2013−01−01.

[4] 徐依吉, 赵红香, 孙伟良, 等. 钢粒冲击岩石破岩效果数值分析[J]. 中国石油大学(自然科学版), 2009, 33(5): 68−69. XU Yiji, ZHAO Hongxiang, SUN Weiliang, et al. Numerical analysis on rock breaking effect of steel particles impact rock[J]. Journal of China University of Petroleum (Edition of Natural Science), 2009, 33(5): 68−69.

[5] 况春雨, 朱志谱, 蒋海军, 等. 单钢粒冲击破岩实验与数值模拟[J]. 石油学报, 2012, 33(6): 1059−1063. KUANG Chunyu, ZHU Zhipu, JIANG Haijun, et al. The experimental study and numerical simulation of single particle impacting rock[J]. Acta Petrolei Sinica, 2012, 33(6): 1059−1063.

[6] 姜美旭. 粒子冲击破岩规律的仿真研究及参数优化[D]. 北京: 北京化工大学机电工程学院, 2011: 21−36. JIANG Meixu. Simulation study and parameter optimization for particle impact rock[D]. Beijing: Beijing University of Chemical Technology. College of Mechanical and Electrical Engineering, 2011: 21−36.

[7] 赵健, 韩烈祥, 徐依吉, 等. 粒子钻井技术理论与现场试验[J]. 天然气工业, 2014, 34(8): 102−107. ZHAO Jian, HAN Liexiang, XU Yiji, et al. Theoretical study and field test of particle impact drilling technology[J]. Natural Gas Industry, 2014, 34(8): 102−107.

[8] SHELDON G L. Effects of surface hardness and other material properties on erosive wear of metals by solid particles[J]. Journal of Engineering Materials and Technology, 1977, 99(2): 133−137.

[9] WVANS A G，GULDEN M E. Impact damage in brittle materials in the elastic-plastic response regime[J]. Proceedings of the Royal Society of London, 1978, 361(1706): 343−365.

[10] ZHAO Jian, ZHANG Guicai, XU Yiji, et al. Mechanism and effect of jet parameters on particle waterjet rock breaking[J]. Powder Technology, 2017, 313: 231−244.

[11] WANG J, GUO D M. A predictive depth of penetration model for abrasive water jet cutting of polymer matrix composites[J]. Journal of Materials Processing Technology, 2002, 121(2): 390−394.

[12] MOMBER A W. Effects of target material properties on solid particle erosion of geomaterials at different impingement velocities[J]. Wear, 2014, 319(1/2): 69−83.

[13] MOMBER A W, KOVACEVIC R. Hydro-abrasive erosion of refractory ceramics[J]. Journal of Materials Science, 2003, 38(13): 2861−2874.

[14] HASHISH M. AWJ milling of gamma titanium aluminide[J]. Journal of Manufacturing Science and Engineering Transactions of the ASEM, 2010, 132(4): 410051−410059.

[15] VIEIRA R E, MANSOURI A, MCLAURY B S, et al. Experimental and computational study of erosion in elbows due to sand particles in air flow[J]. Powder Technology, 2016, 288: 339−353.

[16] HADAVI V, MORENO C E, PAPNI M. Numerical and experimental analysis of particle fracture during solid particle erosion (part I): modeling and experimental verification[J]. Wear, 2016, 356/357: 135−145.

[17] PENG W S, CAO X W. Numerical simulation of solid particle erosion in pipe bends for liquid–solid flow[J]. Powder Technology, 2016, 294: 266−279.

[18] NSOESIE S, LIU R, CHEN K Y, et al. Analytical modeling of solid-particle erosion of stellite alloys in combination with experimental investigation[J]. Wear, 2014, 309(1/2): 226−232.

[19] 张少峰, 曹会敏, 刘燕, 等.弯管中液固两相流及壁面碰撞磨损的数值模拟[J]. 河北工业大学学报, 2008, 37(3): 48−54. ZHANG Shaofeng, CAO Huimin, LIU Yan, et al. Numerical simulation of liquid-solid two-phase flow and erosion-collision in a syphon[J]. Journal of Hebei University of Technology, 2008, 37(3): 48−54.

[20] 林哲. 闸阀内部气固两相流动及磨损研究[D]. 杭州: 浙江大学机械工程学系, 2013: 43−59. LIN Zhe. Research on gas solid flow and solid particle erosion in gate valve[D]. Hangzhou: Zhejiang University.Department of Mechanical Engineering, 2013: 43−59.

[21] 丁矿, 朱宏武, 张建华, 等. 直角弯管内液固两相流固体颗粒冲蚀磨损分析[J]. 油气储运, 2013, 32(3): 241−246.DING Kuang, ZHU Hongwu, ZHANG Jianhua, et al. Erosion wear analysis of solid particles in liquid-solid two-phase flow of right-angle bend pipe[J]. Oil & Gas Storage and Transportation, 2013, 32(3): 241−246.

[22] 董刚, 张九渊. 固体粒子冲蚀磨损研究进展[J]. 材料科学与工程学报, 2003, 21(2): 307−312.DONG Gang, ZHANG Jiuyuan. Developments of research on the solid particle erosion of materials [J].Journal of Materials Science &Engineering, 2003, 21(2): 307−312.

[23] 李剑峰, 龚宝龙, 贾秀杰, 等. 离心式空压机内固粒对叶轮磨损的数值模拟[J]. 中南大学学报(自然科学版), 2013, 44(10): 4047−4054.LI Jianfeng, GONG Baolong, JIA Xiujie, et al. Numerical simulation of solid particle erosion in centrifugal air compressor impeller[J].Journal of Central South University (Science and Technology), 2013, 44(10): 4047−4054.

[24] 廉晓庆, 蒋明学. 基于有限元模拟研究不同形状磨料对高铝砖的冲蚀磨损[J]. 硅酸盐学报, 2014, 42(6): 761−767.LIAN Xiaoqing, JIANG Mingxue. Erosion wear of high alumina brick impacted by erodent particles with different shapes based on finite element method[J].Journal of the Chinese Ceramic Society, 2014, 42(6): 761−767.

[25] 李建庄, 孙德顺, 余畅, 等. 几种材料的固体粒子冲蚀磨损性能[J]. 金属热处理, 2013, 38(11): 37−40.LI Jianzhuang, SUN Deshun, YU Chang, et al. Solid particle erosion wear resistance of several materials[J]. Heat treatment of Metals, 2013, 38(11): 37−40.

[26] 吴波, 严宏志, 徐海良, 等. 渣浆泵内固相颗粒冲蚀特性的数值模拟[J]. 中南大学学报(自然科学版), 2012, 43(1): 124−129.WU Bo, YAN Hongzhi, XU Hailiang, et al. Numerical simulation about erosion characteristics of solid particle in slurry pump[J]. Journal of Central South University (Science and Technology), 2012, 43(1): 124−129.

[27] 鲍崇高, 潘伟, 苗赫濯, 等. 磨粒粒径对Si3N4结构陶瓷冲蚀磨损性能的影响[J]. 西安交通大学学报, 2005, 39(11): 1219−1222.BAO Chonggao, PAN Wei, MIAO Hezhuo, et al. Effect of abrasive particle size on anti-abrasion performance of Si3N4ceramics[J]. Journal of Xi’an Jiaotong University, 2005, 39(11): 1219−1222.

[28] 马振中. 粒子冲击钻井中粒子流动特性的数值模拟及相关试验研究[D]. 北京: 北京化工大学机电工程学院, 2012: 25−42. MA Zhenzhong. Experimental research and numerical simulation of particles flowing property in particle impact drilling system[D]. Beijing: Beijing University of Chemical Technology. College of Mechanical and Electrical Engineering, 2012: 25−42.

[29] 许光文, 葛蔚, 李静海. 颗粒流体两相流模拟方法的讨论和展望[J]. 应用基础与工程科学学报, 1994, 22(2): 139−146.XU Guangwen, GE Wei, LI Jinghai. Prospects of modeling particle-fluid two-phase flow[J]. Journal of Basic Science and Engineering, 1994, 22(2): 139−146.

[30] 韩占忠. FLUENT-流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2009: 260−291. HAN Zhanzhong. FLUENT-fluid simulation calculating examples and engineering application[M]. Beijing: Beijing Institute of Technology Press, 2009: 260−291.

[31] ZAMANI M, SEDDIGHI S, NAZIF H R. Erosion of natural gas elbows due to rotating particles in turbulent gas-solid flow[J]. Journal of Natural Gas Science and Engineering, 2017, 40: 91−113

[32] MESSA G V, MALAVASI S. The effect of sub-models and parameterizations in the simulation of abrasive jet impingement tests[J]. Wear, 2017, 370/371: 59−72.

(编辑 刘锦伟)

Bit internal flow passage erosion by solid-liquid two-phase flow impact of particles

ZHAO Jian1, 2, ZHANG Guicai1, 2, XU Yiji1, WANG Ruihe1, ZHOU Weidong1, HAN Liexiang3

(1. College of Petroleum Engineering, China University of Petroleum, Qingdao 266580, China;2. Academy of Science and Technology, China University of Petroleum, Dongying 257061, China;3. Drilling & Production Engineering Technology Research Institute, Chuanqing Drilling Engineering Co. Ltd., CNPC, Deyang 618300, China)

In order to identity the mechanism of bit internal flow passage erosion by solid-liquid two-phase flow impact of particles, the discrete phase model (DPM) was applied to establish the physical model of bit internal flow passage erosion, and the effects of particle parameters on the bit internal flow passage erosion were obtained. Furthermore, the indoor experiments were carried on to verify the validity of the DPM model. The results show that the bit internal flow passage erosion of particles mainly distributes on the contraction surface of bit internal flow passage, and the closer to the bit center axis, the higher the erosion rate is. The average erosion rate of the internal flow passage increases with the increase of the inlet velocity of particles. As the particle diameter increases, the average erosion rate of the internal flow passage decreases first and starts to increases, and then tends to be stable. The minimum average erosion rate is obtained with a particle diameter of 2.0 mm. Furthermore, the average erosion rate of the internal flow passage increases linearly with an increase of the particle volume fraction. When the inlet angle is 50°, the maximum average erosion rate of the internal flow passage appears. In addition, the average erosion rate of the internal has been less affected by the pressure. The erosion loss of the internal flow passage decreases by 0.80% after 100 h erosion experiment.

solid-liquid two-phase flow; bit internal flow passage erosion; discrete phase model (DPM); particle parameters; drilling bit

10.11817/j.issn.1672-7207.2018.05.026

TE248

A

1672−7207(2018)05−1228−09

2017−05−09；

2017−06−28

第58批中国博士后基金资助项目(2015M582167)；山东省自然科学基金资助项目(ZR2016EL10)；中央高校基本科研业务费专项资金资助项目(16CX02061A)；青岛市应用基础研究项目(16-5-1-37-jch)；中石油科学研究与技术开发项目(2015F-1801)；山东省重点研发计划项目(GG201709250112) (Project(2015M582167) supported by the 58th China Postdoctoral Science Foundation; Project (ZR2016EL10) supported by the Natural Science Foundation of Shandong Province; Project(16CX02061A) supported by the Fundamental Research Funds for the Central Universities; Project(16-5-1-37-jch) supported by the Qingdao Applied Basic Research Program; Project(2015F-1801) supported by the CNPC Scientific Research and Technology Development Program; Project(GG201709250112) supported by the Key Research and Development Plan of Shandong Province)

赵健，博士(后)，讲师，从事射流破岩钻井技术等研究；E-mail: zhaojian-666@163.com