利用拟态物理学优化算法的中超赛程优化方法*

万 珺， 何 健

(1.武汉轻工大学 体育部，湖北 武汉 430048;2.武汉轻工大学 数学与计算机学院，湖北 武汉 430048)

对于主客场赛制的联赛，赛程的时间表直接影响各队的行程安排.优秀的赛事组织者会在日程安排上尽量减少一些交通等费用[1].因此，行程成本问题成为多年来重要的优化问题.比赛时间表的优化研究具有如下意义[2]：(1) 降低比赛中各支球队的行程成本；(2) 合理安排比赛间隔，使运动员保持充沛体力.关于行程费用，球队总是乘交通工具往返于城市之间，随着石油价格迅速上涨，交通费用变高.另一个考虑因素是运动员的体力，运动员在没有足够休息时间的情况下连续比赛，会降低比赛竞技能力[3].所以，有必要为每个球队安排公平赛程.

调度大型运动赛程通常是非常困难的，需要考虑特定的运动规则，以及许多常常相互冲突的因素，包括行程距离等.由于存在一个较大的解决方案搜索空间，这个调度过程通过人工完成是相对费时的.目前，一些学者提出了一些赛程编排方案.例如，文献[4]以最小化所有球队的行程距离为目标，提出了一种基于蒙特卡洛的赛程优化方法.文献[5]提出一种基于集成约束规划的赛程优化方法，用来最小化每个球队的转场次数.然而，大多数关于多维分配问题的研究集中在三维问题上，为了使其可以自然扩展到更高维度，这些方法都是利用拉格朗日松弛来识别强边界的分支边界.多维分配问题一般是NP难题，由于问题的复杂性，启发式解决方法能够得到更好的结果.为此，一些学者提出了一些智能搜索算法[6]来搜索最优赛程编排方法，如禁忌搜索、遗传算法、模拟退火算法等，目的是降低比赛中各球队的时间和行程成本.

拟态物理学优化(artificial physics optimization, APO)算法[7]是一种新的智能搜索算法.该算法是受牛顿第二定律启发，通过个体间的虚拟力来调整个体的速度和位置，最终收敛到全局最优解[8].与传统遗传算法和粒子群优化算法相比，APO具有较好的全局搜索和避免陷入局部最优的能力，且收敛速度快、稳定性好[9].为此，本文利用APO算法提出一种赛程优化方法，以中超联赛为例，最小化联赛的总行程距离.实验结果表明提出的方法能够有效减少各队的总行程，具有可行性和有效性.

1 利用APO算法的赛程编排方法

1.1 拟态物理学优化算法(APO)

拟态物理学是由Spear等人在2005年受物理力学而启发提出的一种优化方法.在其基本框架中，问题的解决方案表现为物理个体，每个个体都具有空间质量、速度和扭矩分量.它们的移动受到物理规则的控制.每个个体由于其他个体的虚拟力作用，在搜索空间中寻找最佳位置[10].

在APO算法中，多维范围内非线性目标函数的全局最小位置问题定义为：

min{f(X):X∈Ω⊂Rd},f:Ω⊂Rd→R，

APO算法主要分为3个步骤.

第一步：初始化.随机形成d维决策空间中的组群，并初始化组群中的个体数量N，引力常数G.根据问题类型，粒子的初始速度设定为零.为每个个体计算目标函数值，在t阶段具有最大适应度的个体的位置向量称为最佳x，即xbest.

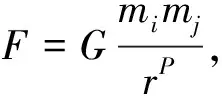
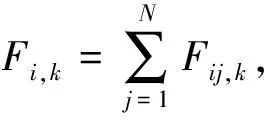
第三步：移动.将个体移动到一个特定的位置，这是根据计算的总力来完成的.这个力被用来计算个体速度和位置的更新.在时间t+1时，个体i的空间坐标和速度由以下等式更新：

式中，α是在[0,1]范围内均匀分布的随机值，0≤w<1是用户定义的惯性值，较大的w会引起较大的速度变化.

1.2 目标函数

在本文中，赛程编排的目标函数是所有球队的总行程距离.同时设定了一些惩罚函数，目标是使优化算法快速接近最优可行解.让不可行的解决方案进入种群非常重要，因为良好的解决方案通常是在可行和不可行的解决方案之间进行培育的结果.在这里，我们以两支球队所在城市的最短公路距离作为路程度量.目前百度地图的应用非常广泛，从中提取距离信息是非常方便且有效的，以此来计算各球队之间的确切距离.那么，适应度函数由下式给出：

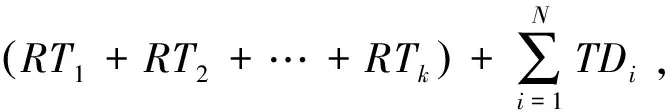
式中，h表示惩罚权重，设置为100，RTk表示所违反约束的编号，TDi表示球队i行程的总里程.

约束条件：RT1表示每支球队的主场城市之间的距离是固定的，且往返行程也相同.RT2表示每支球队客场打完一场比赛后不回主场城市休息，直接转到下场比赛城市.RT3表示每支球队连续两场比赛之间的间隔不少于1天.

1.3 赛程编排优化的基本步骤

本文采用了一种新的智能搜索算法来进行赛程编排优化，即拟态物理学优化算法.编排优化的基本步骤如下：步骤1，输入参数和约束条件，例如球队数量、距离信息、比赛持续时间等.步骤2，生成随机时间编排表种群，并获取总行程距离.步骤3，计算编排表的适应度函数，并通过拟态物理学优化算法进行寻优.步骤4，将当前获得的局部最优解与全局最优解进行比较，计算施加在每个个体上的力，并更新个体的速度和位置.步骤5，待算法收敛或达到最大迭代次数，获得最终的最优方案.

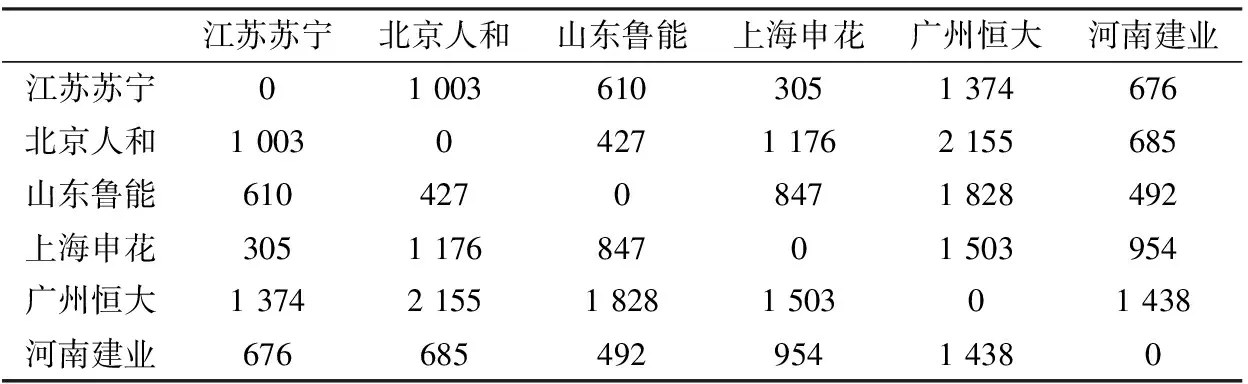
表1 各队之间的公路距离

2 实验及分析

2.1 实验设置

进行了一个验证性实验来证明所提出方法的可行性.为了简化描述，选择了2018年中超比赛中的6支球队进行巡回赛.巡回赛为每支球队都与其他球队进行比赛，最终以积分来排名.6支球队分别为江苏苏宁、北京人和、山东鲁能、上海申花、广州恒大和河南建业.巡回赛中，每天只比赛一场，整个赛程共30天.赛程优化的目标是实现最小化所有球队的行程距离总和.在这个例子中，我们设定各城市之间的公路距离是固定的，如表1所示.另外，对于拟态物理学优化算法，设置参数为种群数量N=50，惯性权重w=0.5，引力常数G=0.09.

2.2 结果分析

为了更好地进行性能分析，将本文方法与文献[4]方法进行比较，两种方法获得的最优赛程编排方案如表2和表3所示.其中，“建业-恒大”表示“建业”队为主场球队，“恒大”队为客场球队.可以看到，每支球队分别和其他5支球队进行主客场共10场比赛，整个赛程为30场比赛.

从表2和表3可以看出，文献[4]方法中的赛程安排没有本文方法的科学，文献[4]方法中的第20和第21场比赛中，恒大队连续两天进行比赛，虽然都是在主场比赛，但这样也很消耗队员体力，不能很好地保证公平性.而在本文方法的赛程安排中，没有一支球队会连续比赛.

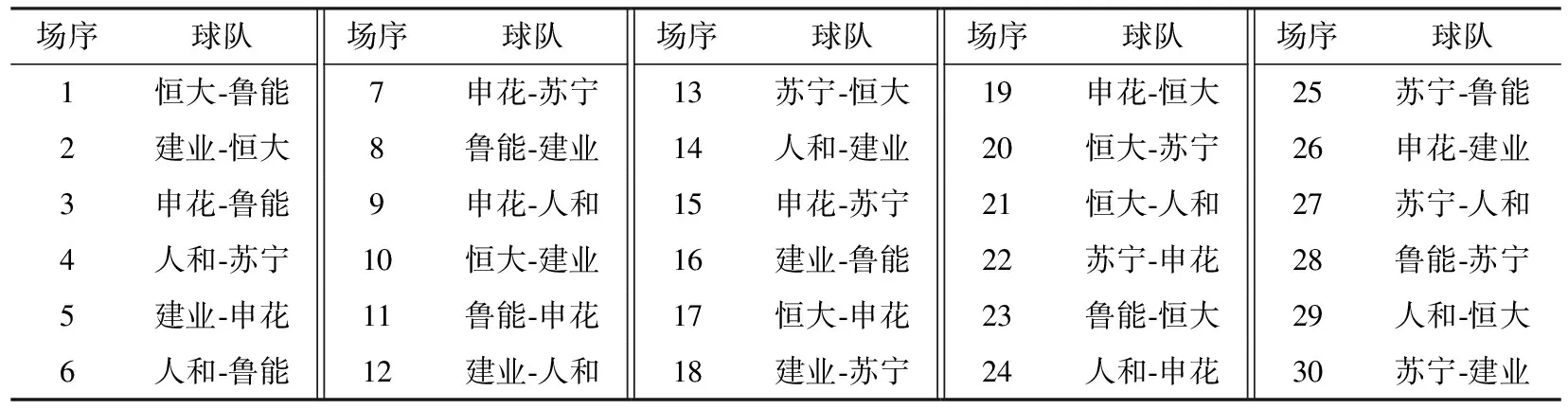
表2 文献[4]方法获得的赛程编排方案

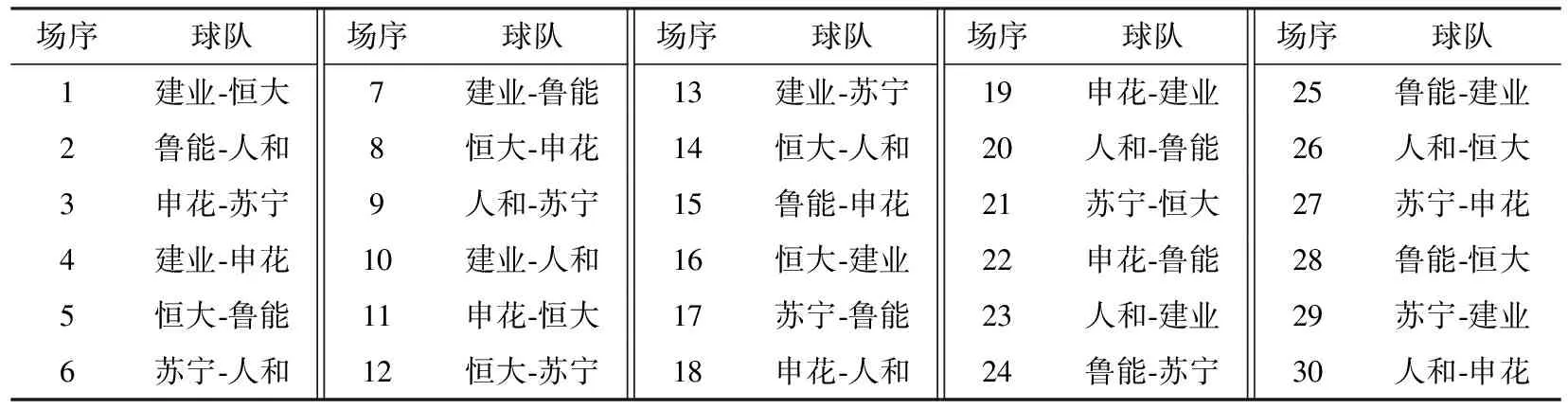
表3 本文方法获得的赛程编排方案

为了更加清晰地显示两种赛程编排方案的行程，表4给出了统计结果.可以看出，本文方法的赛程编排方案中，江苏苏宁、山东鲁能、上海申花、广州恒大和河南建业这5支队伍的行程距离都有所降低，只有北京人和的行程稍微增加.本文赛程编排方案的总行程为46 807 km，比文献[4]方案减少了2 997 km，优化率为6.02%，证明了本文方法的有效性和可行性，可以为中超比赛等类似比赛进行赛程编排优化.

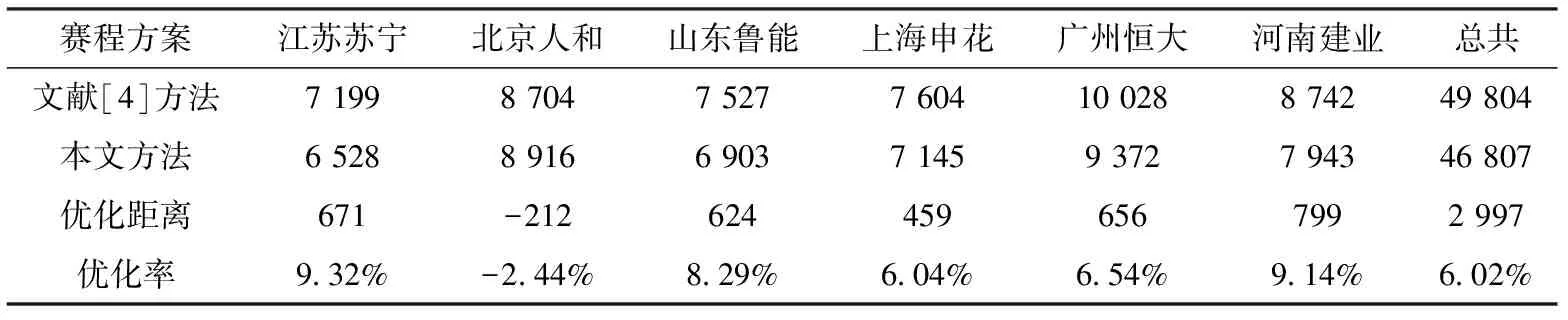
表4 两种赛程方案的行程距离对比

3 结 论

为了提高中超联赛的赛程经济性，提出了一种利用拟态物理学优化算法的赛程优化方法.根据百度地图获取每支球队主场之间的公路距离，以最小化总行程距离为目标，通过APO算法获得一个最佳赛程编排方案.结果表明在具有6支队伍的比赛编排实验中，本文方法的编排方案更加合理有效，大大降低了球队行程距离.

参考文献

[1] 曾芳,桂赵曼.体育联赛中基于GSO算法的赛程优化方法[J]. 湘潭大学自然科学学报, 2018, 40(1),72-76.

[2] HAO G, ZHANG J. Design and practice of the competition schedule arrangement system of swimming sports based on artificial intelligence[C]// International Conference on Real Time Intelligent Systems. Springer, Cham, 2016:440-454.

[3] HUANG G, PING L, WANG Q. A hybrid metaheuristic ACO-GA with an application in sports competition scheduling[C]// International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/distributed Computing. IEEE, 2007:611-616.

[4] 都扬扬, 木仁. 具有主客场赛制的各大联赛赛程优化安排与设计[J]. 中国管理科学, 2015，23(1):171-175.

[5] LARSON J, JOHANSSON M, CARLSSON M. An integrated constraint programming approach to scheduling sports leagues with divisional and round-robin tournaments[C]// International Conference on AI and OR Techniques in Constriant Programming for Combinatorial Optimization Problems. Springer International Publishing, 2014:144-158.

[6] 刘岚,兰小毅.基于MILP模型和QPSO算法的绿色物流调度方法[J]. 湘潭大学自然科学学报, 2018, 40(1): 77-81.

[7] 沈林成, 王祥科, 朱华勇,等. 基于拟态物理法的无人机集群与重构控制[J]. 中国科学:技术科学, 2017,47(3): 266-285.

[8] JIA B, ZHONG P, ZHU F. Adaptive artificial physics optimization of reservoir flood regulation[J]. Journal of Hydroelectric Engineering, 2016, 35(8):32-41.

[9] TEEPARTHI K, KUMAR D M V. Security-constrained optimal power flow with wind and thermal power generators using fuzzy adaptive artificial physics optimization algorithm[J]. Neural Computing & Applications, 2016:1-17.

[10] 谢丽萍,曾建潮.基于拟态物理学方法的全局优化算法[J]. 计算机研究与发展, 2011,48(5):848-854.