交换半环上全矩阵代数的局部Jordan导子

庄金洪

(福建商学院 基础部，福建 福州，350012)

1.引言与预备知识

关于Jordan导子的研究一直是国内外众多学者关注的热点问题，其中“Jordan导子什么时候退化成导子”已被许多学者讨论。由局部Jordan导子的定义可知，Jordan导子一定是局部Jordan导子，局部Jordan导子不一定是Jordan导子。而近来，赵延霞[1]通过对交换幺环上全矩阵代数的Jordan导子和局部Jordan导子的研究，证明了交换幺环上的全矩阵代数上的每一个Jordan导子都是内导子，每一个局部Jordan导子也都是内导子。对于交换半环上全矩阵代数的局部Jordan导子是否也有类似的结论呢？本文的研究旨在解决这个问题，并得到肯定的答案。

定义1[2]：半环R=(R,+,·,0,1)是满足下列性质的一种代数结构：

(1) (R,+,0)是一个交换幺半群；

(2) (R,·,1) 是一个幺半群；

(3) 对任意的a,b,c∈R，均有a·(b+c)=a·b+a·c,(a+b)·c=a·c+b·c；

(4) ∀a∈R,0·a=a·0=0；

(5) 0≠1。

半环R称为交换半环，如果∀a,b∈R,均有ab=ba。

半环R称为2-非挠的，如果对于任意的a,b∈R,如果2a=2b，那么a=b。

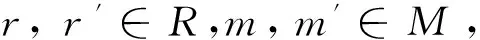
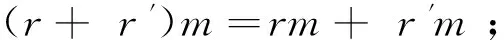
(4) 1Rm=m;

(5)r0M=0M=0Rm;

则称M为左R-半模。

定义3[3]：设R是一个交换半环，(A,+,·,0,1)是一个半环。如果(A,+,0)是一个左R-半模，且满足∀r∈R,x,y∈A，均有r(xy)=x(ry)，则称A是R上的一个代数。

定义4[4]：设R是一个交换半环，Mn(R)是由R上所有n阶矩阵构成的集合。对于A=(aij),

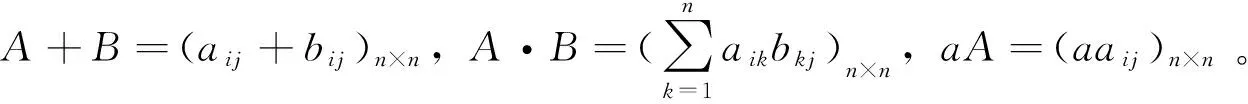
不难验证，(Mn(R),+,On)对于纯量乘法构成一个左R-半模，称为交换半环R上的矩阵半模，其中零元On是n阶零矩阵。而(Mn(R),+,·,On,In)是交换半环R上的一个代数，称为交换半环R的全矩阵代数。本文将第(i,j)处元素为1、其它位置的元素均为0的n×n矩阵记作eij。

定义5[4]：设R是一个半环，r∈R，如果在R中存在一个元素s使得r+s=0，则称r为半环R的一个可反元，此时称s为r的一个反元。

容易验证，可反元r的反元是唯一的,记为-r。设a,b∈R，b是R的可反元，定义a-b=a+(-b)。

定义6[4]：设R是一个交换半环，M=(aij)n×n∈Mn(R),如果M中的每一个元素aij都是R中的可反元，那么称M在Mn(R)中是可反的，这时称(-aij)n×n为M的反矩阵，记为-M。

定义7：设A是R上的一个代数。

(1) 对于线性映射δ：A→A，如果对于∀a,b∈A，均有δ(ab+ba)=δ(a)b+aδ(b)+δ(b)a+bδ(a)，则称δ是一个Jordan 导子。

(2) 对于线性映射δa：A→A，如果对于∀a∈A，存在一个仅依靠于a的Jordan导子δa,使得δ(a)=δa(a)，则称δa是一个局部Jordan 导子。

2.主要结果及其证明

引理1[4]：设R是一个2-非挠的交换半环，A是半环R上的一个代数，δ是A上的一个Jordan导子。那么对于∀a∈A，均有δ(a2)=δ(a)a+aδ(a)。

引理2：设R是一个2-非挠的交换半环，δ是Mn(R)上的一个局部Jordan导子。

(1)如果E是Mn(R)上的一个幂等元，那么δ(E)=δ(E)E+Eδ(E)。

(2)如果E3=E，E∈Mn(R)，那么δ(E)=δ(E)E2+Eδ(E)E+E2δ(E)。

证明：(1)如果E是Mn(R)上的一个幂等元，那么E=E2。因为δ是Mn(R)上的一个局部Jordan导子，那么存在一个仅依靠于E的Jordan导子δE，使得δ(E)=δE(E)。因此，由引理2.1有：

δ(E)=δE(E)=δE(E2)=δE(E)E+EδE(E)=δ(E)E+Eδ(E)。

(2)因为δ是Mn(R)上的一个局部Jordan导子，那么存在一个仅依靠于E的Jordan导子δE,使得δ(E)=δE(E)。如果E=E3，那么：

δE(E·E2+E2·E)

=δE(E)·E2+EδE(E2)+δE(E2)E+E2δE(E)(Jordan导子的定义)

=δE(E)·E2+E(δE(E)E+EδE(E))+(δE(E)E+EδE(E))E+E2δE(E)(由引理2.1)

=δE(E)·E2+EδE(E)E+E2δE(E)+δE(E)E2+EδE(E)E+E2δE(E)

=2(δE(E)·E2+EδE(E)E+E2δE(E))

而δE(E·E2+E2·E)=δE(2E3)=2δE(E3)，所以2δE(E3)=2(δE(E)·E2+EδE(E)E+E2δE(E))。由于R是一个2-非挠的交换半环，所以δE(E3)=δE(E)·E2+EδE(E)E+E2δE(E)。

因此，δ(E)=δE(E)=δE(E3)=δE(E)·E2+EδE(E)E+E2δE(E)=δ(E)·E2+Eδ(E)E+E2δ(E)。

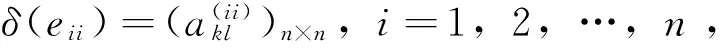
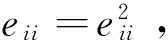
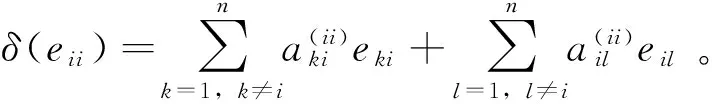
引理5：设R是一个2-非挠的交换半环，δ是Mn(R)上的一个局部Jordan导子，那么存在一个可反矩阵M，使得(δ-adM)(eii)=0，i=1,2,…，n。

证明：因为(eii+ejj)2=eii+ejj,∀i≠j，所以由引理2可知：

δ(eii+ejj)

=δ(eii+ejj)(eii+ejj)+(eii+ejj)δ(eii+ejj)

=(δ(eii)+δ(ejj))(eii+ejj)+(eii+ejj)(δ(eii)+δ(ejj))

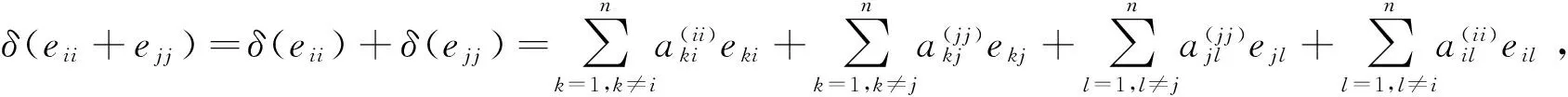
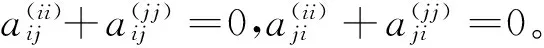
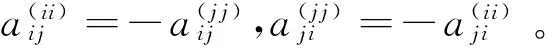
(δ-adM)(eii)

=δ(eii)-adM(eii)=δ(eii)-(Meii-eiiM)

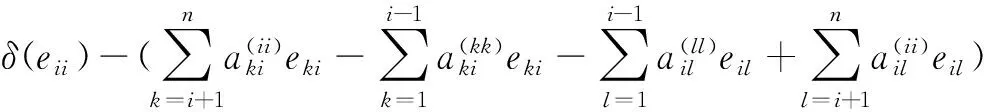
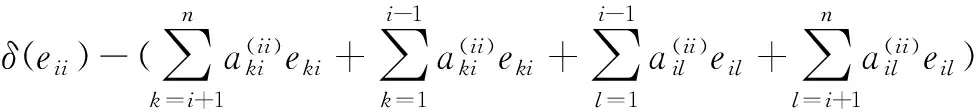
=0。

引理6：设R是一个2-非挠的交换半环，且R中不存在非零的加法幂等元，δ是Mn(R)上的一个局部Jordan导子，如果δ(eii)=0，i=1,2,…，n,那么存在一个bij∈R，使得δ(eij)=bijeij,1i≠jn。

证明：因为δ是Mn(R)上的一个局部Jordan导子，那么存在一个仅依靠于eij的Jordan导子δeij，使得δ(eij)=δeij(eij)。

因为(eii+eij)2=eii+eij,所以由引理2可知：

δ(eii+eij)

=δ(eii+eij)(eii+eij)+(eii+eij)δ(eii+eij)

=(δ(eii)+δ(eij))(eii+eij)+(eii+eij)(δ(eii)+δ(eij))

=δ(eij)(eii+eij)+(eii+eij)δ(eij)

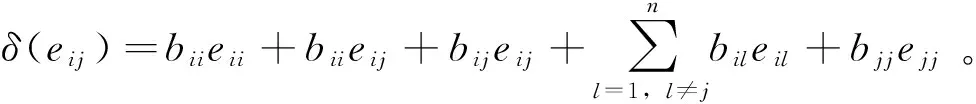
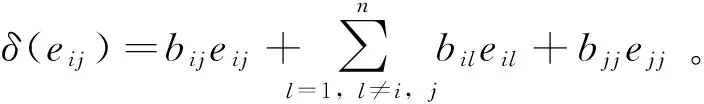
另一方面，又因为(eij+ejj)2=eij+ejj,所以由引理2可知：

δ(eij)

=δ(eij+ejj)=δ(eij+ejj)(eij+ejj)+(eij+ejj)δ(eij+ejj)

=δ(eij)(eij+ejj)+(eij+ejj)δ(eij)

=bijeij+bjjejj+bjjejj+bjjeij,

对比等式两边，可得:bjjejj=bjjejj+bjjejj，再由R的条件，有bjj=0。因此，δ(eij)=bijeij。

引理7：设R是一个2-非挠的交换半环，且R中不存在非零的加法幂等元，δ是Mn(R)上的一个局部Jordan导子，如果δ(eii)=0，i=1,2,…，n，那么存在一个可反矩阵D∈Mn(R)，使得：

(δ-adD)(ei,i+1)=0,(δ-adD)(ei+1,i)=0,1in-1，且(δ-adD)(eii)=0，1in。

证明：由引理6，当δ(eii)=0，i=1,2,…，n时，δ(eij)=bijeij。

因为(eij+eji)3=eij+eji,所以由引理2(2)，有：

δ(eij+eji)

=δ(eij+eji)·(eij+eji)2+(eij+eji)·δ(eij+eji)·(eij+eji)+(eij+eji)2δ(eij+eji)

=(δ(eij)+δ(eji))·(eii+ejj)+(eij+eji)·(δ(eij)+δ(eji))·(eij+eji)+(eii+ejj)(δ(eij)+δ(eji))

=(bijeij+bjieji)·(eii+ejj)+(eij+eji)·(bijeij+bjieji)·(eij+eji)+(eii+ejj)(bijeij+bjieji)

=bjieji+bijeij+(bijeji+bjieij)+bijeij+bjieji

=(bij+bji+bij)eij+(bji+bij+bji)eji

而δ(eij+eji)=δ(eij)+δ(eji)=bijeij+bjieji，所以bij=bij+bji+bij,bji=bji+bij+bji。

因此，bij+bji=(bij+bji+bij)+bji=(bij+bji)+(bij+bji),再由R的条件，可得：bij+bji=0。

所以，bji=-bij。

可设可反矩阵D=-diag(0,b12,b12+b23,…,b12+b23+…+bn-1,n)，则：

(δ-adD)(eii)=0-(Deii-eiiD)=0,1in;

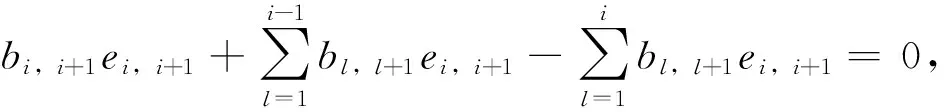
(δ-adD)(ei+1,i)=bi+1,iei+1,i-(Dei+1,i-ei+1,iD)

引理8：设R是一个2-非挠的交换半环，且R中不存在非零的加法幂等元，δ是Mn(R)上的一个局部Jordan导子，如果δ(ei,i+1)=0,δ(ei+1,i)=0,1in-1，且δ(eii)=0，1in，那么：

δ(ei,i+k)=0,δ(ei+k,i)=0,∀ei,i+k,ei+k,i∈Mn(R)。

证明：由引理6，当δ(eii)=0，i=1,2,…，n时，δ(eij)=bijeij。

当k=2时，因为

(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)2=ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1，所以：

δ(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)

=δ(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)·(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)+(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)·δ(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)

=δ(ei,i+2)·(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)+(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)·δ(ei,i+2)

=bi,i+2ei,i+2·(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)+(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)·bi,i+2ei,i+2=0,

而δ(ei,i+1+ei+1,i+2+ei,i+2+ei+1,i+1)=δ(ei,i+1)+δ(ei+1,i+2)+δ(ei,i+2)+δ(ei+1,i+1)=δ(ei,i+2)，因此，δ(ei,i+2)=0。

类似的，由(ei+1,i+ei+2,i+1+ei+2,i+ei+1,i+1)2=ei+1,i+ei+2,i+1+ei+2,i+ei+1,i+1可得：δ(ei+2,i)=0。

假设δ(ei,i+m)=0,δ(ei+m,i)=0,m=2,3,…,k-1。

因为ei,i+1+ei+1,i+k+ei,i+k+ei+1,i+1与ei+1,i+ei+k,i+1+ei+k,i+ei+1,i+1均为幂等元，所以类似于k=2，经计算可得:δ(ei,i+k)=0,δ(ei+k,i)=0。

因此，由数学归纳法可知:δ(ei,i+k)=0,δ(ei+k,i)=0, ∀ei,i+k,ei+k,i∈Mn(R), 即δ(eij)=0。

定理1:设R是一个2-非挠的交换半环，且R中不存在非零的加法幂等元，那么Mn(R)上的每个局部Jordan导子都是内导子。

证明：令δ是Mn(R)上的一个局部Jordan导子，那么由引理4到引理8可得：存在可反矩阵M,D∈Mn(R)，使得(δ-adM-adD)(eij)=0,1i,jn。也就是说δ=adM+adD=ad(M+D)，所以δ是Mn(R)上的一个内导子。

参考文献:

[1]ZHAO Y X. Jordan derivations and local Jordan derivations on full matrix algebras over commutative rings[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis，2014，47(6):98-104.

[2]GOLAN J S. Semirings and their applications [M].London:Kluwer Academic Publisher，1999.

[3]陈培慈.半环理论与语言和自动机[M].南昌:江西高校出版社，1993.

[4]庄金洪. 交换半环上全矩阵代数的Jordan导子[J].龙岩学院学报，2017，35(2):35-39.