利用MGSA算法的光学图像加密增强方案*

宋福英， 王永斌， 赵 丽

(1.甘肃省高等学校农村电商人才培养重点实验室，甘肃 成县 742500; 2.陇南师范高等专科学校，甘肃 成县 742500; 3.山西大学 软件学院，山西 太原 030013)

网络技术的迅猛发展使得通信进入了新时代，处理通信的安全问题变得很重要，由此相关研究提出了许多加密技术方案[1-3].尽管很多加密技术对文本消息都可用，但是由于遗传性质，难以适用于光学图像加密[4-5].

为了提升光学图像通信的安全性，国内外学者进行了不少相关研究[6-10].例如，文献[10] 的方案通过混沌序列将光学图像的红色、绿色和蓝色成分分离成3个二维矩阵，同时应用置换，将矩阵的每个8×8块当成一个单元进行加密，该方案抵抗统计性暴力攻击的能力较弱.

本文提出改进盖师贝格-撒克斯通算法(modified Gerchberg-Saxton algorithm, MGSA)的光学图像加密增强方案，修改逻辑映射，改正逻辑映射的一些缺点，如稳定窗口、空白窗口和序列的不均匀分布等，从而在保留高度相关性的前提下生成更大的密钥空间，提高加密的效率.

1 方案

1.1 改进盖师贝格-撒克斯通算法

不同于传统盖师贝格-撒克斯通算法(Gerchberg-Saxton algorithm, GS)[11]，提出的改进盖师贝格-撒克斯通算法更加适用于具有多次迭代的振幅函数g(x1,y1)，可从振幅函数中衍生出纯相位函数Ψg(x0,y0).提出的MGSA框架如图1所示，λ是入射平面波的波长，z表示输入空间域(x0,y0)和傅里叶域(x1,y1)之间的距离，确定的纯相位函数(phase-only function, POF)Ψg(x0,y0)将记录进选择映射(selected mapping, SLM)，变成纯相位掩膜(phase-only mask, POM).

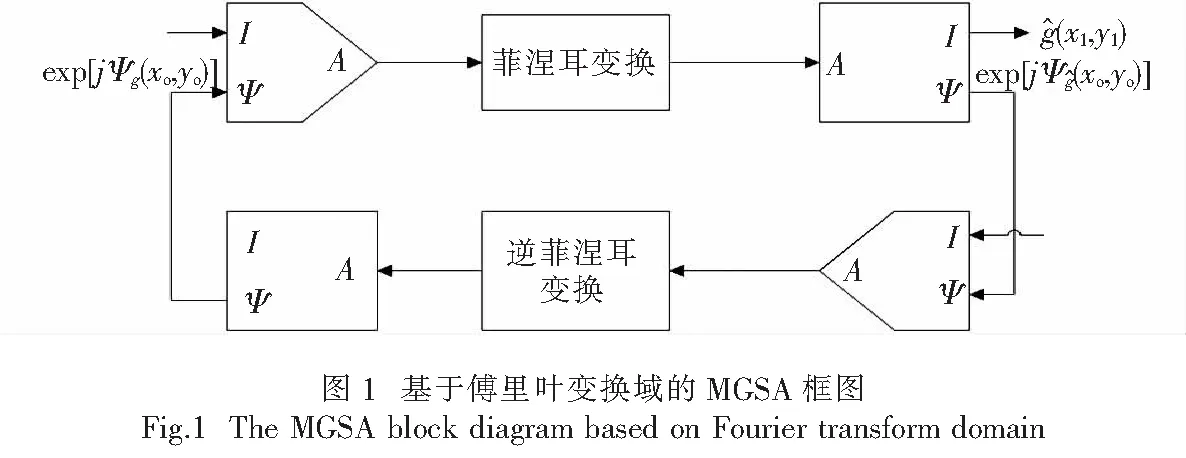
1.2 图像加密

提出的方案使用修改的逻辑映射进行密钥生成，文献[11]中介绍的修改的逻辑映射的定义为：

xn+1=[μ×M×xn(1-xn)]mod 1, 其中，0≤x≤1,n∈Z,0<μ≤4且M>1.

文献[11]表明，修改的逻辑映射改正了逻辑映射的一些缺点，如稳定窗口、空白窗口和序列的不均匀分布.在修改的逻辑映射中，可将μ×M当成一个参数，而不用将μ和M考虑成两个不同的参数.因为μ×M可以取任意正实值，所以可以将这个值当成密钥的一部分，因此这个映射还可以增加密钥空间.在这个算法中，修改的逻辑映射用以生成两个混沌序列，它们用于像素置乱、比特交换和像素值的随机扩散.

令明文图像的大小为H×W，其中，H和W代表像素中明文图像的高度和宽度.将明文图像储存在3个二维阵列R、G和B中，分别表示每个维数H×W的红色、绿色和蓝色信道.X0,X1∈(0,1)是初始值，且M0、M1是修改的逻辑映射的参数，其值取正实值.生成H×W的两个序列(序列1).

序列1:

T1(1)=X0

T2(1)=X1

对于I=2:H×W

T1(I) =(M0×T1(I-1)×

(1-T1(I-1)))mod 1

T2(I)=(M1×T2(I-1)×

(1-T2(I-1)))mod 1

结束

序列2:

RP(1)=⎣X0×H」+1

RP(1)=⎣X1×H」+1

S1(1)=⎣X0×255」+1

S2(1)=⎣X1×255」+1

对于I=2:H×W

S1(I)=⎣T1(I)×255」+1

S2(I)=⎣T2(I)×255」+1

结束

对于I=2:H

RP(I)=⎣T1(I)×H」+1

结束

对于I=2:W

CP(I)=⎣T1(I×W)」+1

结束

使用两个序列T1和T2生成另外4个序列RP、CP、S1和S2.序列RP和CP用于置换行和列之一.序列S1和S2用于比特交换和随机扩散.生成的4个序列RP、CP、S1和S2为序列2.

加密涉及像素置乱、比特交换和随机扩散.使用一对一映射其上实现随机扩散，它们将像素位置(i,j)映射到图像上的其他一些的像素位置(i′,j′)上.图2为图像加密的结构图.

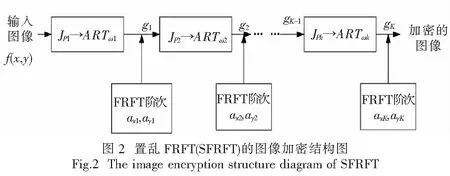
f(x,y)表示待加密的二维图像，K是迭代次数，k表示第k次迭代，其中1≤k≤K.

令A={(i,j):1≤i≤H,1≤j≤W}.定义映射Λ:A→AbyΛ(i,j)=(t1,t2),1≤t1≤H,1≤t2≤W,式中：t1=(u1×i+M1)modH+1，t2=(u2×j+M2)modH+1，u1,u2,M1,M2是随机选择的整数，使得gcd(u1,H)=1,gcd(u2,W)=1.

2 实验结果与分析

搭建实验测试平台以验证所提出算法的有效性.实验测试平台基于MATLAB实现，采用的图形尺寸为512×512像素，基于Beagleboard-xM进行图像处理和加密操作过程.

2.1 加密性分析

首先，测试加密方案对密钥变换的灵敏度.使用第一种密钥集X和第二种密钥M加密相同的图像，得到像素变化率(NPCR)和平均改变强度(UACI)，如表1所示.

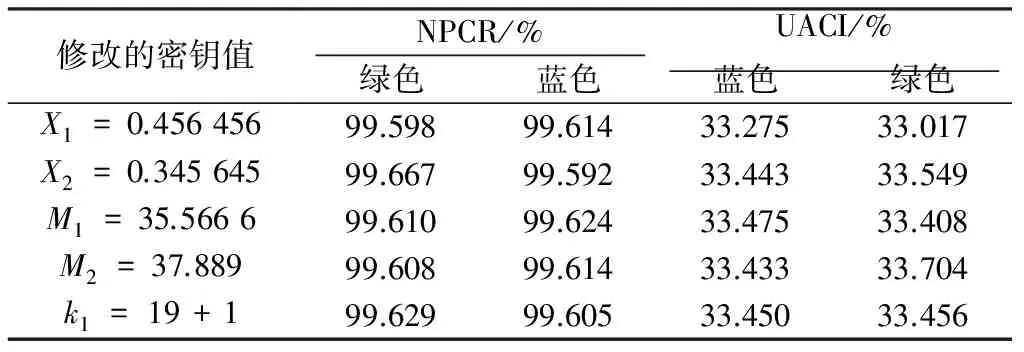
表1 密钥灵敏度

提出的方案使用两种混沌序列，且使用两个不同初始条件和参数的修改逻辑映射生成序列.此外，还将随机扩散期间选择的4个随机整数μ1、μ2、M1、M2当成密钥空间，每个空间为8位，因此，提出方案的密钥空间为2232，足以安全抵抗统计性暴力破解.而文献[10]中给出的修改逻辑映射的密钥空间为100位，密钥空间为2200，抵抗统计性暴力破解的能力相对较弱.

2.2 相关性分析

对明文图像和加密图像的横向相邻性、垂直相邻性和对角相邻性进行相关分析.因为当密文图像分布均匀时，明文图像高度相关，实验过程中，对这些像素值的分布进行研究，并利用式(1)和表2中的值计算相关系数.文献[10]的明文图像的相关系数更接近零，而高度不相关的密文图像无法给出明文图像的信息，本文方案显然优于文献[10]的方案.

(1)

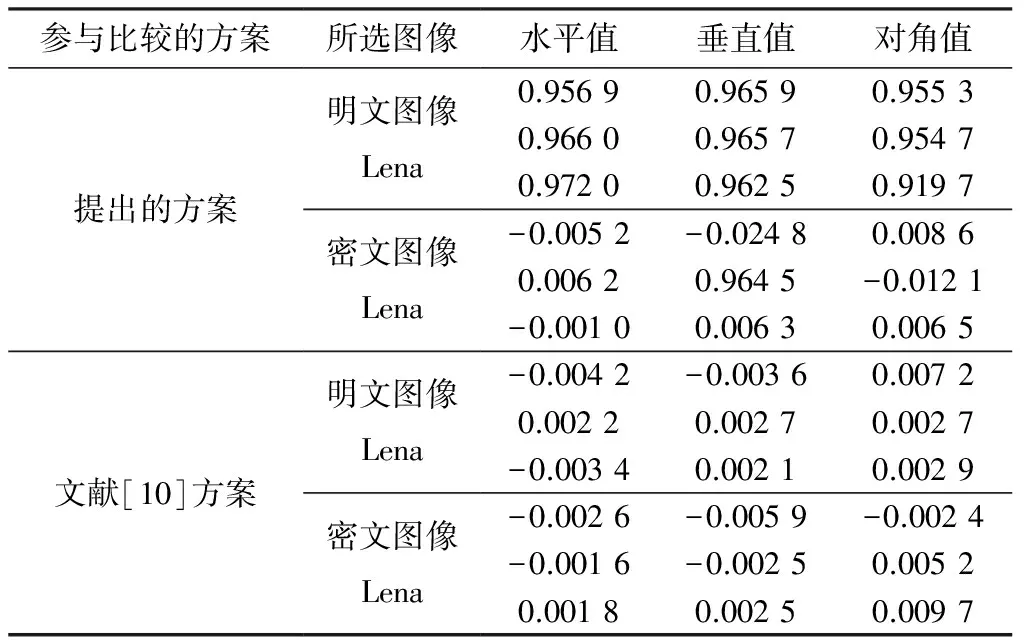
表2 相关系数

3 结 论

针对JPEG图像加密方案的安全问题，在分析混沌映射和MGSA算法的基础上，提出一种新的使用修改逻辑映射的图像加密方案.修改的逻辑映射生成两种混沌序列，序列选择行交换和列交换，以解决像素置乱和像素值修改.在位级别，通过随机交换像素中所选的位数修改每个像素值，并根据随机扩散原则，使用密钥选择下一个将扩散的像素位置.实验分析表明，提出的方案可以更好地抵抗统计和差分攻击，具有较强的实用性.

参考文献

[1] 徐亚, 张绍武. 基于Arnold映射的分块双层自适应扩散图像加密算法[J]. 中国图象图形学报, 2015, 20(6):740-748.

[2] 吕福起, 李霄民.利用MLT和SRS的混合图像融合与去噪算法[J]. 湘潭大学自然科学学报, 2018, 40(1): 111-114.

[3] 李敬医, 陈炬桦.基于3D混沌映射和细胞自动机的图像加密方案[J]. 计算机科学, 2015, 42(7): 182-185.

[4] XU Y, XIE C, WANG Y, et al. Chaos projective synchronization of the chaotic finance system with parameter switching perturbation and input time-varying delay[J]. Mathematical Methods in the Applied Sciences, 2016, 38(17): 4279-4288.

[5] 易永红, 张小洪. 对抗通信中的军事图像加密与隐藏传输系统设计[J]. 湘潭大学自然科学学报, 2017, 39(2): 96-100.

[6] FEMG Y, PU J, WEI Z. Switched generalized function projective synchronization of two hyperchaotic systems with hidden attractors[J]. European Physical Journal Special Topics, 2015, 224(8): 1593-1604.

[7] PHAM V T, VAIDYANATHAN S, VOLOS C, et al. A no-equilibrium hyperchaotic system with a cubic nonlinear term[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(6): 3259-3265.

[8] 廖琪男, 卢守东, 孙宪波. 结合超混沌序列和移位密码的数字图像加密算法[J]. 小型微型计算机系统, 2015, 36(2): 332-337.

[9] FRANÇOIS M, GRPSGES T, BARCHIESI D, et al. A new image encryption scheme based on a chaotic function[J]. Signal Processing Image Communication, 2012, 27(3): 249-259.

[10] BIGDELI N, FARID Y, AFSHAR K. A novel image encryption/decryption scheme based on chaotic neural networks [J].Engineering Applications of Artificial Intelligence, 2012, 25(4): 753-765.

[11] HWANG H E, CHANG H T, LIE W N. Multiple-image encryption and multiplexing using a modified Gerchberg-Saxton algorithm and phase modulationin Fresnel-transform domain[J].Optics letters, 2009, 34(24): 3917-3919.