初始形状对石墨烯基底上的铂金属纳米薄膜动力学演化过程影响的研究*

李艳茹， 范银萍， 陈 琼， 彭海艳

(湘潭大学 物理与光电工程学院，微纳能源材料与器件湖南省重点实验室，湖南 湘潭 411105)

近年来，薄膜材料的表面吸附，汽车零部件的镀膜工艺，表面的润滑与自清洁工艺越来越受到人们的重视.金属纳米薄膜材料具有大的比表面积，由此引起的小尺寸效应、表面效应、自组装效应、量子尺寸效应以及宏观量子隧道效应等使其在材料、生命、化学、光子学、信息科学等领域具有更加广泛的应用前景.

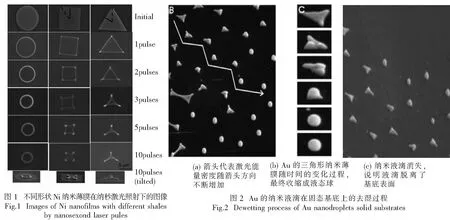
在实验上，Rack等[1]采用纳秒激光照射不同形状的镍的薄膜，观察到如图1所示的实验现象.从图中可以看出，镍薄膜受热后开始熔化，薄膜向内收缩，拐角处(曲率较大)收缩较明显.圆形因为边缘的曲率一致，所以边缘收缩均匀；三角形和正方形因为边缘曲率不一致，所以收缩不均匀.最终不同形状的镍金属薄膜都向中心收缩成为颗粒.

Habenicht等[2]利用纳秒激光照射热解石墨或玻璃上的Au的三角形薄膜，同样观测到了Au的纳米液滴在固态基底上由边缘向中心聚集的演化过程，并且观察到了金属液滴脱离基底表面的现象,如图2所示.

在计算机模拟研究方面，Fuentes-Cabrera等[3]采用分子动力学方法模拟了不同形状的Cu纳米薄膜在石墨基底的演化过程，得到了与实验类似的结论：Cu的金属薄膜从曲率较大的拐角处开始收缩，初始结构为圆形的薄膜比形状为三角形或四边形的薄膜收缩快，而后形成球冠状液滴.这些液滴最终可能受基底粘滞作用的影响沉积或脱离基底表面.液滴脱离基底表面的脱离速度随温度升高而升高.初始形状为圆形的Cu薄膜形成的液滴的脱离速度比其他形状大.

一定温度下，金属薄膜在基底上的动力学演化过程受多种因素的共同影响，研究这种多重因素影响的动力学演化有助于我们理解实际的热解过程，有助于人们建立合理的参考模型来研究更为普适的动力学演化内在规律.

本文通过分子动力学的方法模拟了高温条件下不同形状的单层Pt的纳米薄膜在固态石墨烯基底上的动力学演化过程，分析了初始薄膜形状、厚度对Pt金属薄膜动力学演化过程的影响,并进一步分析了产生这些影响的原因.

1 计算方法和模型

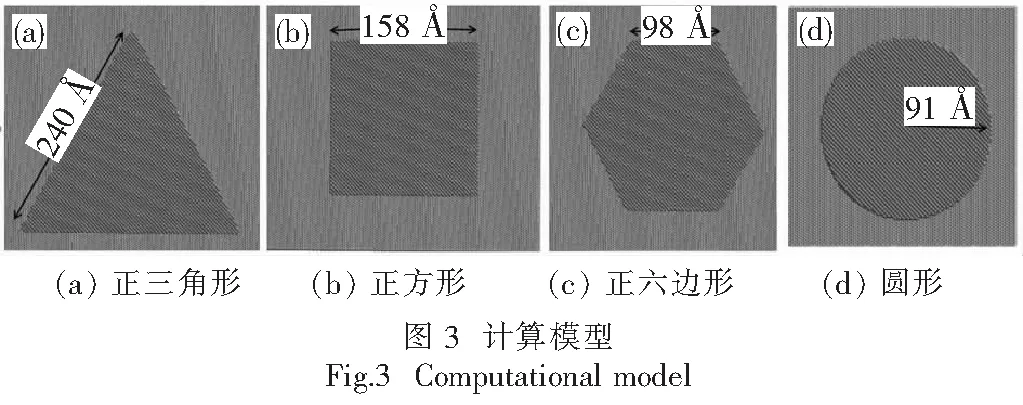
对于铂的金属薄膜模型，我们首先在Materials Studio中建立了Pt的面心立方(FCC)块体结构,晶格常数为3.92 Å，并从它的块体结构中沿<100>方向截取了面积约为24 952 Å2的不同形状的单层金属纳米薄膜，然后置于石墨烯基底上，作为我们动力学模拟的初始结构.如图3所示，Pt金属纳米薄膜的形状有正三角形、正方形、正六边形，边长分别为240 Å，158 Å，98 Å，以及半径为91 Å的圆形.这些不同形状的薄膜都是由3 226个Pt原子组成的单层纳米薄膜，金属原子层与基底表面的初始距离约为3.0 Å.石墨烯基底的尺寸为295.14 Å×306.72 Å(包含34 560个碳原子)，基底尺寸都远大于铂金属纳米薄膜的尺寸，因而可以忽略近邻模拟单胞中金属薄膜之间的相互作用.

我们构建出面积相同的正三角形、正方形、正六边形、圆形的单层金属铂纳米薄膜，放于单层石墨烯基底表面，用分子动力学的方法来模拟短暂高温(2 700～3 800 K)下薄膜的动力学演化过程.

分子动力学方法是在原子、分子水平上求解多体问题的重要的计算机模拟方法.认为模型中每个原子都遵循牛顿运动学的规律，一旦粒子的初始条件(如起始位置和初始速度)和运动方程中的受力状况确定，系统就可被精确求解.我们利用分子动力学模拟的开源软件包LAMMPS来模拟不同形状的Pt纳米薄膜在固态石墨烯基底上的动力学演化过程[4-5].对于分子动力学来说，原子间的相互作用是基础，势函数的精确性直接影响模拟的准确度.对于势函数的选择，我们查阅了大量的文献，选定了适合研究模型的势函数类型，期待得到较为准确的结果.我们的模型中两种金属元素Pt-Pt之间选用嵌入原子势(embedded-atom method,EAM)[6]，已有大量计算结果证实，EAM势能够很好地描述金属元素在不同温度和压强下的动力学过程.单层石墨烯基底C-C原子之间的相互作用，采用Tersoff势进行描述.金属Pt和基底C原子之间采用勒让德-琼斯(LJ)势[3,6-7].Pt-C体系的LJ参数ε=0.040 92 eV,σ=2.936 Å[9].ε越大说明薄膜和基底的相互作用越强，我们可以通过调节ε来预测其势阱深度对薄膜演化的影响.

因为我们想要研究金属薄膜的去湿或沉积问题，所以边界条件采用X、Y方向为周期性的边界条件，Z方向上为非周期性的边界条件.对于计算过程中温度的设定，我们选取高温(2 700～3 800 K)但不超过铂金属的沸点(Pt金属的沸点约为4 100 K).整个模型在NVT正则系综下进行模拟，单层石墨烯基底完全固定.开始时先对薄膜进行驰豫，使其达到稳定结构，再在恒定高温下进行加热，模拟的时间步长为2 fs[3].

2 结果与讨论

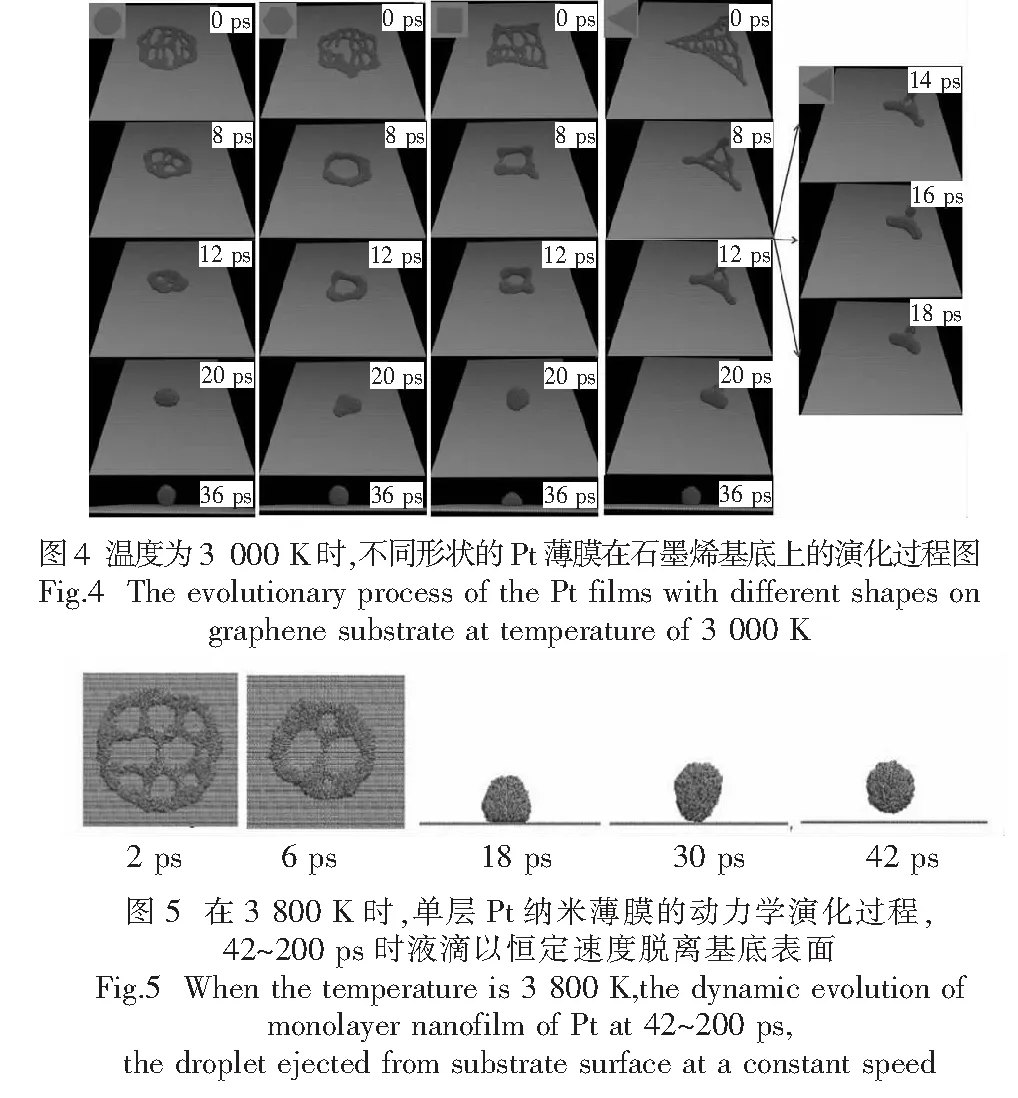
不同形状的铂的纳米薄膜在石墨烯基底上的动力学演化过程如图4所示.一定温度范围下(2 700～3 800 K)，单层Pt的纳米液膜破裂，形成不同大小的纳米空洞.在薄膜表面张力的作用下，纳米Pt金属薄膜由边缘向中心收缩，开始收缩发生在曲率大的拐角处，此现象在正三角形薄膜的收缩过程中观察得尤为明显.如图4所示，正三角形薄膜的动力学演化过程中,16 ps时薄膜收缩为三脚架的形状.边缘收缩的同时纳米空洞融合、增大，空洞数目减少，然后空洞收缩、变小，最终完全消失，Pt原子汇聚形成纳米液滴.液滴形成球冠状，温度较低时，纳米液滴沉积在了石墨烯基底表面(如图4)；温度较高时液滴会脱离基底，从表面发射出去(如图5).

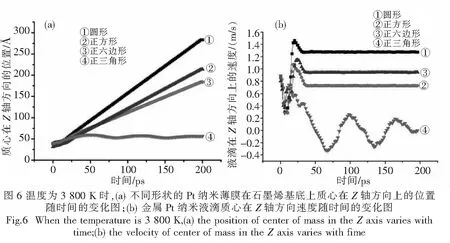
从图4 中可以看到，在相同温度下，圆形薄膜收缩速度更快，方形薄膜的沉积更为明显.我们想了解高温下Pt的液滴在石墨烯上的运动情况，计算了不同形状的Pt的金属液滴在3 800 K时质心在Z轴方向上的位置与时间关系，如图6(a)所示.通过对质心位置的时间求导得出了液滴在Z轴方向的速度与时间的关系，如图6(b)所示.从图中可以看出，圆形、正方形、六边形金属薄膜的液滴在Z轴方向上最后脱离了基底表面且以恒定的速度向上运动，而正三角形薄膜的液滴速度图像呈现不规则的波浪形，表明正三角形薄膜的液滴最终沉积在了石墨烯基底表面.在温度为3 800 K时，圆形薄膜的液滴脱离速度最大，正方形的最小，正三角形薄膜的液滴没有脱离基底.这可能是由于薄膜的表面能转化为了液滴向上运动的动能的关系.液态薄膜在收缩过程中，拐角处薄膜的收缩消耗了大量的能量，且曲率越大，薄膜在收缩时消耗的表面能也越大，导致液薄在形成液滴脱离基底时动能越小.这些得出的结论与Rack[1]和Fuentes-Cabrera[3]所得出的结论类似.由此说明表面能对Pt液滴的脱离速度的影响很大.

为了深入分析表面积对Pt液滴分离速度的影响.我们构建了原子数相同，层数不同的Pt纳米薄膜圆盘结构，放于单层石墨烯上进行分子动力学模拟.图7为纳米Pt薄膜在原子数相同的情况下(同为7 540个原子)初始结构为3层(半径8 nm，曲线(a))，4层(半径6.9 nm，曲线(b))，5层(半径6.2 nm，曲线(c))的纳米薄膜脱离速度随温度的变化图.(d)和(e)分别表示圆盘半径为8 nm的4层和5层纳米Pt薄膜的脱离速度随温度的变化图..

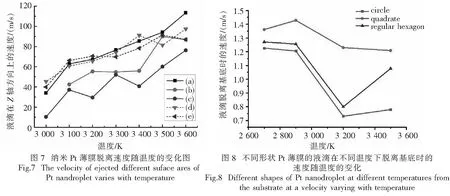
从图中可以得出：Pt的薄膜在组成原子数相同的情况下，层数越大脱离速度越小.原子数相同，薄膜层数较大时，薄膜的半径肯定会很小，薄膜的表面积也会很小.上述结论可以描述为：在薄膜组成原子数相同的情况下，初始金属薄膜的表面积越小金属液滴脱离速度越小.通过图中(c)和(e)线或(b)和(d)线之间的比较可以得出：在金属薄膜层数相同的情况下，半径小的液滴脱离速度也小.也就是说，在金属薄膜层数相同的情况下，初始金属薄膜的表面积越小金属液滴脱离速度越小.进一步表明薄膜收缩时表面能转化为了Pt液滴脱离基底的动能.

为进一步了解形状对液滴脱离速度的影响，调节Pt-C体系的LJ参数ε为0.01 eV，将基底与薄膜的相互作用减小，计算不同形状的Pt金属液薄对液滴脱离速度的影响.得到了与之前研究不同的结论，如图8所示.当基底与薄膜的相互作用减小时，在一定温度下，圆形薄膜形成液滴脱离基底表面的速度较小，正方形薄膜形成液滴脱离基底表面的速度较大.这可能是由于薄膜的层数较少，在去湿的过程中都有孔洞的形成，这些空洞在收缩过程中增加了液滴与基底之间的粘滞力.粘滞力对液滴脱离基底的动能有了主导性的影响.

3 结 论

通过分子动力学方法研究了不同形状的单层纳米金属薄膜Pt在石墨烯基底刚性表面的快速热过程，纳米薄膜相变后破裂收缩成核过程中，表面张力让液滴向上，粘滞力让液滴向下，表面能转化为动能，Z方向上拉长液滴.当液滴底部半径缩小到0 mm时，如果液滴重心仍有向上移动的速度，由于惯性,液滴将以该速度为脱离速度，离开刚性基底表面而向上运动.如果没有向上的动能，液滴会沉积在基底表面.液滴的脱离速度与初始形状有关.当ε=0.02 eV时，一定温度下圆形薄膜的液滴脱离速度较大，正三角形的较小.当ε=0.01 eV时，正方形薄膜的液滴脱离速度较大,圆形的较小.相同原子数的薄膜，层数越多，液滴的脱离速度越小.薄膜的动力学演化过程受表面张力，纳米孔洞收缩时与基底的粘滞力，金属薄膜原子与基底原子间的库仑力等共同作用的影响，是一个复杂的动力学过程.根据我们的结论，可通过控制薄膜形状、薄膜厚度、温度等来控制金属薄膜成核脱离基底的过程，这在镀膜工艺、涂料、表面吸附以及自清洁材料方面有着广泛的应用前景.

参考文献

[1] RACK P D, GUAN Y, FOWLKES J D, et al. Pulsed laser dewetting of patterned thin metal films: a means of directed assembly[J]. Applied Physics Letters, 2008, 92(22):59.

[2] HABENICHT A, OLAPINSKI M, BURMEISTER F, et al. Jumping nanodroplets.[J]. Science, 2005, 309(5743):2043-2045.

[3] FUENTES-CABRERA M, RHODES B H, BASKES M I, et al. Controlling the velocity of jumping nanodroplets via their initial shape and temperature[J]. Acs Nano, 2011, 5(9):7130-7136.

[4] WU X, ZHAO H, ZHONG M, et al. Molecular dynamics simulation of graphene sheets joining under ion beam irradiation[J]. Carbon, 2014, 66(3):31-38.

[5] YUAN Q, ZHAO Y P. Multiscale dynamic wetting of a droplet on a lyophilic pillar-arrayed surface[J]. Journal of Fluid Mechanics, 2013, 716(2):171-188.

[6] LI X, HE Y, WANG Y, et al. Dewetting properties of metallic liquid film on nanopillared graphene[J]. Scientific Reports, 2014, 4(4):3938.

[7] NGUYEN T D, FUENTESCABRERA M, FOWLKES J D, et al. Competition between collapse and breakup in nanometer-sized thin rings using molecular dynamics and continuum modeling[J]. Langmuir the Acs Journal of Surfaces & Colloids, 2012, 28(39):13960-13967.

[8] SANKARANARAYANAN S K R S, BHETHANABOTLA V R, JOSEPH B. Molecular dynamics simulations of the structural and dynamic properties of graphite-supported bimetallic transition metal clusters[J]. Physical Review B, 2005, 72(19):195405.

[9] 李艳茹, 何秋香, 王芳,等. 金属纳米薄膜在石墨基底表面的动力学演化?[J]. 物理学报, 2016, 65(3):239-245.

[10] LI Y, TANG C, ZHONG J, et al. Dewetting and detachment of Pt nanofilms on graphitic substrates: A molecular dynamics study[J]. Journal of Applied Physics, 2015, 117(6):2401-2409.