基于常权编码的光学相机通信闪烁抑制研究

耿秋实,张文英,戴永恒

(中国电子科学研究院，北京 100041)

0 引 言

光学相机通信(OCC: Optical camera communication)是一种可见光通信技术，其特点在于使用在相机中的图像传感器检测光信号。由于图像传感器的泛在发展趋势，OCC在智能交通系统、基于位置服务和增强现实等[1]领域的应用得到了广泛的研究。在OCC系统中，数据的表达是通过变化发光二极管(LED: light emitting diode)的光强来实现的，因此LED的主要功能，即照明，则受到闪烁的威胁。为了抑制闪烁到不影响照明功能的水平，在任一时刻，给定时间区间T内的平均光强变化必须控制在较小的水平，T不大于10 ms[2]。为了实现这一目标，频移调制[2-3]、曼彻斯特编码[4]和其他线路编码[5]技术等引起了研究者的兴趣。常权编码(CWC: constant-weight coding)是一种重要的线路编码技术，已被广泛用于通信纠错。它可以把输入的字符转换为平均强度恒定的码字，因此适合用来实现抑制闪烁的目的。一个常权编码有三个特性参数，CWC(n，m，w)，其中n是输出码字的长度(单位为码元)，m是输入字符的长度(单位为码元)，w是权重(每个码字中码元1的比例)。编码效率和平均强度分别由m/n和w/n定义。经典地，常权编码的核心问题是在给定码字长度n，最小汉明距离d，和权重w的条件下，找到最多的二进制码字数A(n，d，w)[6-7]。在OCC系统中，我们追求尽可能高的净速率和尽可能小的闪烁，因此需要在给定码字长度n和选定最高编码效率的条件下，寻找一个常权编码方案，既能提供尽可能高的编码效率又能平滑强度的变化。在本文中，我们提出了一种快速有效的算法，在给定码字长度n的条件下，寻找满足要求的常权编码方案，并通过数值仿真验证了算法的有效性。

1 方法与仿真

照明闪烁是由发射机调制LED的光强后，在给定时间区间T内的平均光强不断变化引起的。考虑一个极端的情况，在区间T中只存在一个码元，则T内的平均光强最大可能，Imax，是代表符号1的全亮时的光强， 而最小可能，Imin，是代表符号0的全暗时的光强。此时，照明闪烁最严重。我们定义对比度(CR: contrast ratio)来衡量某种情况下区间T内的平均光强的变化程度，即闪烁，由公式(1)计算

(1)

显然，CR越大，照明闪烁越显著。

图1 区间T中的N个码元构成的K个完整码字和两个残缺码字(a)最小可能平均光强的情况(b)最大可能平均光强的情况。CW：码字。

普遍地，区间T中的码元越多，由于随机性，平均光强的变化越小。因此，抑制闪烁的第一步是需要足够高的码元率。但长1符号序列和长0符号序列的存在使得即使在高码元率的情况下，闪烁仍然存在。采用常权编码将符号1和符号0组成的各种字符转化为强度恒定的码字，即可避免长符号序列的影响。当采用常权编码后，整个码元流的平均光强在w/n附近波动。波动是由在区间T两端的残缺码字造成的。如图1所示，区间T中的N个码元构成K个完整码字和两个残缺码字。这两个残缺码字的平均光强可能是极小值Imin，如图1(a)所示，或极大值Imax，如图1(b)所示。

残缺码字的存在扰乱了区间T内的平均光强的稳定性。优化常权编码的目的就是要尽量减少两个残缺码字的干扰。在优化过程中，从常权编码CWC (n,m,w)的码字空间X中选取一个大小为2m的子集，基于该子集形成的常权编码方案对随机输入的符号流进行编码，形成的码元流将具有最小的对比度。

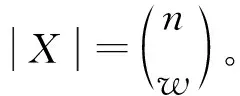
我们提出了一个基于跳的算法，以快速搜索最优的编码表来抑制闪烁。跳定义为码元从符号1到符号0或符号0到符号1的变化。内跳定义为在码字内的一跳，外跳则在两个码字连接时可能出现。在给定码字空间X时，每个码字的内跳数和外跳数可分别用算法1和算法2计算。

算法 1

输入: 码字 Xi=[x1,x2,…,xn-1,xn], i=1,2,…,|X|输出: 内跳数 IH(Xi)第1步: Xif=[x1,x2,…,xn-1], Xib=[x2,…,xn-1,xn]第2步: 按位减法, Xifb=Xif-Xib第3步: 求Xifb元素的绝对和, IH(Xi)=sum(abs(Xifb))

可以发现，码字的内跳数实际上是Xif到Xib的汉明距离。

算法 2

输入: 码字 Xi=[x1,x2,…,xn-1,xn],i=1,2,…,|X|, 和码字空间 X输出: 外跳数 OH(Xi)第1步: 码字以符号1开头的概率 pb=以符号1开头的码字数X码字以符号1结尾的概率pe=以符号1结尾的码字数X第2步: OH(Xi)=xor(x1,1)*pe+xor(x1,0)*(1-pe)+xor(xn,1)*pb+xor(xn,0)*(1-pb)

一个码字Xi的总跳数是内跳数和外跳数之和。

H(Xi)=IH(Xi)+OH(Xi)

在码元流中存在的跳越多，长1和长0的长度则越小。在闪烁抑制最佳的编码表中，我们选择常权编码CWC (n,m,w)的码字空间X中跳数最多的前2m个码字，如算法3所示。

算法3

输入: 跳数 H(Xi),i=1,2,3,…,|X|, 和码字空间 X 输出: 最佳码表{Xi}, i=1,2,3,…,2m第1步: H(Xi) 降序排列, i=i1,i2,i3,…,iX第2步:最佳码表 {Xi}, i=i1,i2,i3,…,i2m

接下来通过数值仿真验证基于跳算法的有效性。在仿真中，输入的随机字符数目设置为1000。字符流由常权编码转换为码字流。码字流的码元用矩形脉冲表示，经过20倍上采样，得到信号波形。我们沿着波形滑动一个窗口，计算窗口中信号的平均光强，找到整个波形中的最小平均光强Imin和最大平均光强Imax。闪烁抑制性能由CR来量化，如公式(1)中定义的。计算平均光强的窗口大小是S，单位为码元。当S=100，T=10毫秒时，码元率是10k波特。由于码元率受到LED和照相机带宽的限制，我们希望在尽可能小的窗口中可以达到抑制闪烁的水平。在仿真中，我们改变S值来评估不同编码表的闪烁抑制性能：S从1增加100，每次增加0.05个码元。我们比较了从基于跳算法中得到的最佳编码表的CR曲线(CR相对于窗口大小S)与所有其他编码表的CR曲线。

2 结果和讨论

首先给定码字长度n，改变权重w，为每个常权编码CWC (n,m,w)计算出最大的m值，即获得最高的编码效率，结果如表1所示。可以看到，编码效率随着码字长度n的增大而提高。表1中也给出了常权编码CWC (n,m,w)的码表数量；它随码字长度n的爆炸性增加是显而易见的。

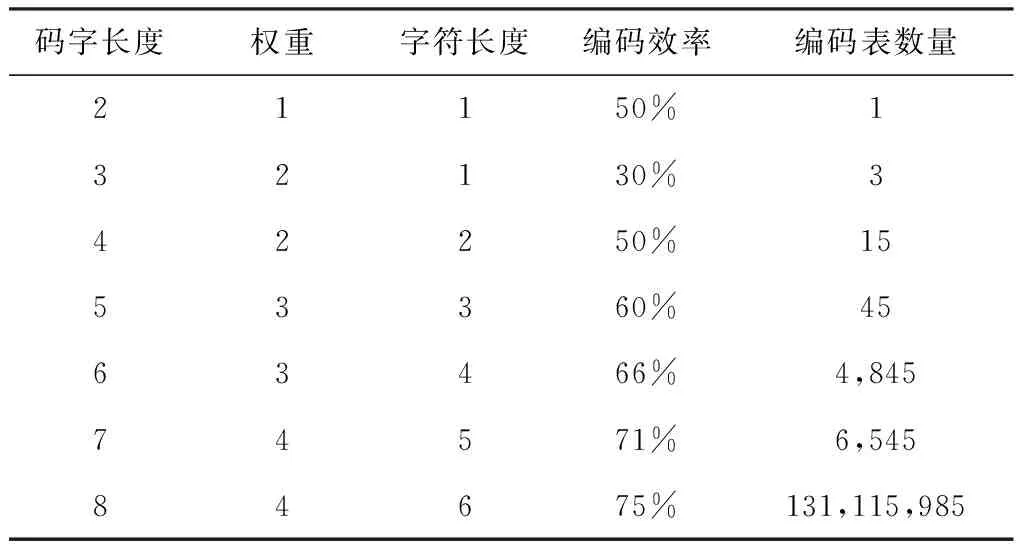
表1 CWC的编码效率和编码表数量

图2展示的是闪烁抑制最佳的码表和其他码表之间的对比度(CR)曲线的对比，包括CWC(3,1,2), CWC(4,2,2), CWC(5,3,3), 和 CWC(6,4,3)。蓝色粗线是基于跳算法给出的最优编码表的CR曲线，红色细线是所有其他编码表的CR曲线，虚线是CR=2%水平线。插图是放大的CR曲线，放大部位是窗口大小S从90到100个码元的位置。在所有的情况下，最优编码表的CR曲线都低于其他码表的CR曲线，证实了基于跳算法的有效性。时间效率方面，基于跳算法和暴力算法的时间消耗如表2所示。在同一台计算机上，基于跳算法的时间消耗远小于暴力算法，特别是对于较长的码字。当码字长度为6时，基于跳算法的时间消耗比暴力算法低4个数量级。

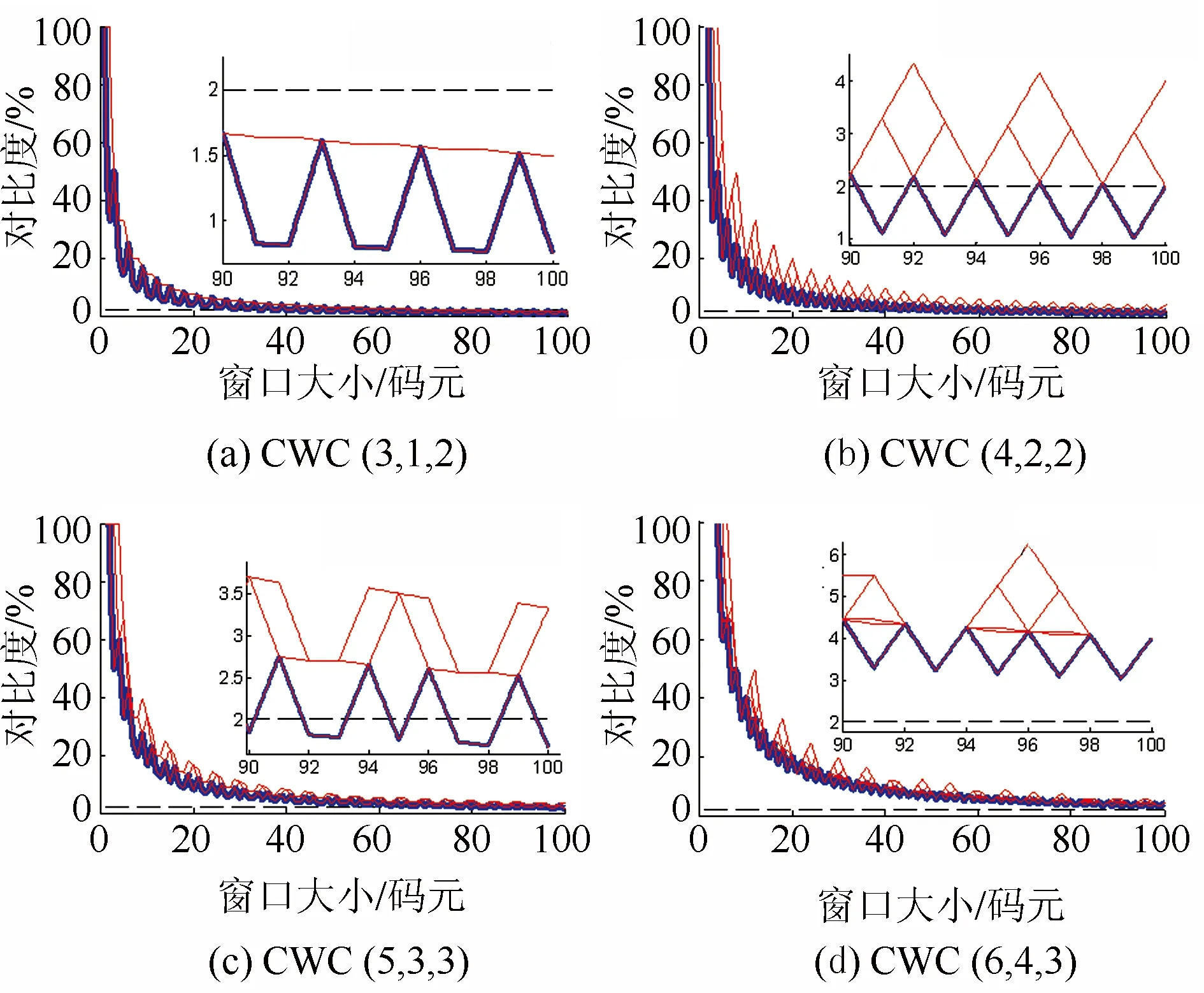
图2 CR曲线的对比

常权编码跳算法暴力算法CWC(3, 1, 2)2.7070 s8.1070 sCWC(4, 2, 2)3.7410 s53.4730 sCWC(5, 3, 3)4.5630 s231.1540 sCWC(6, 4, 3)6.0990 s3.4765× 104 s

图3显示了不同常权编码的闪烁抑制最优编码表的CR曲线。我们发现CR通常会随码字长度的增加而增加，虽然编码效率也在同趋势提升。在OCC系统，常权编码的选择应基于闪烁抑制和编码效率之间的平衡。一般来说，如果OCC系统可以支持较高的码元率，则可以用高编码效率的CWC。否则，编码效率必须牺牲，以保障LED首要的照明功能。此外，我们的结果展示了一些可以改善闪烁抑制性能的策略。对于相同的码字长度和编码效率，较大的权重会带来较小的CR，如CWC(7, 5, 3)和CWC(7, 5, 4)所示。CWC(7, 5, 4)也优于CWC(6, 4, 3)，他们具有接近的CR但CWC(7, 5, 4)的编码效率更高。

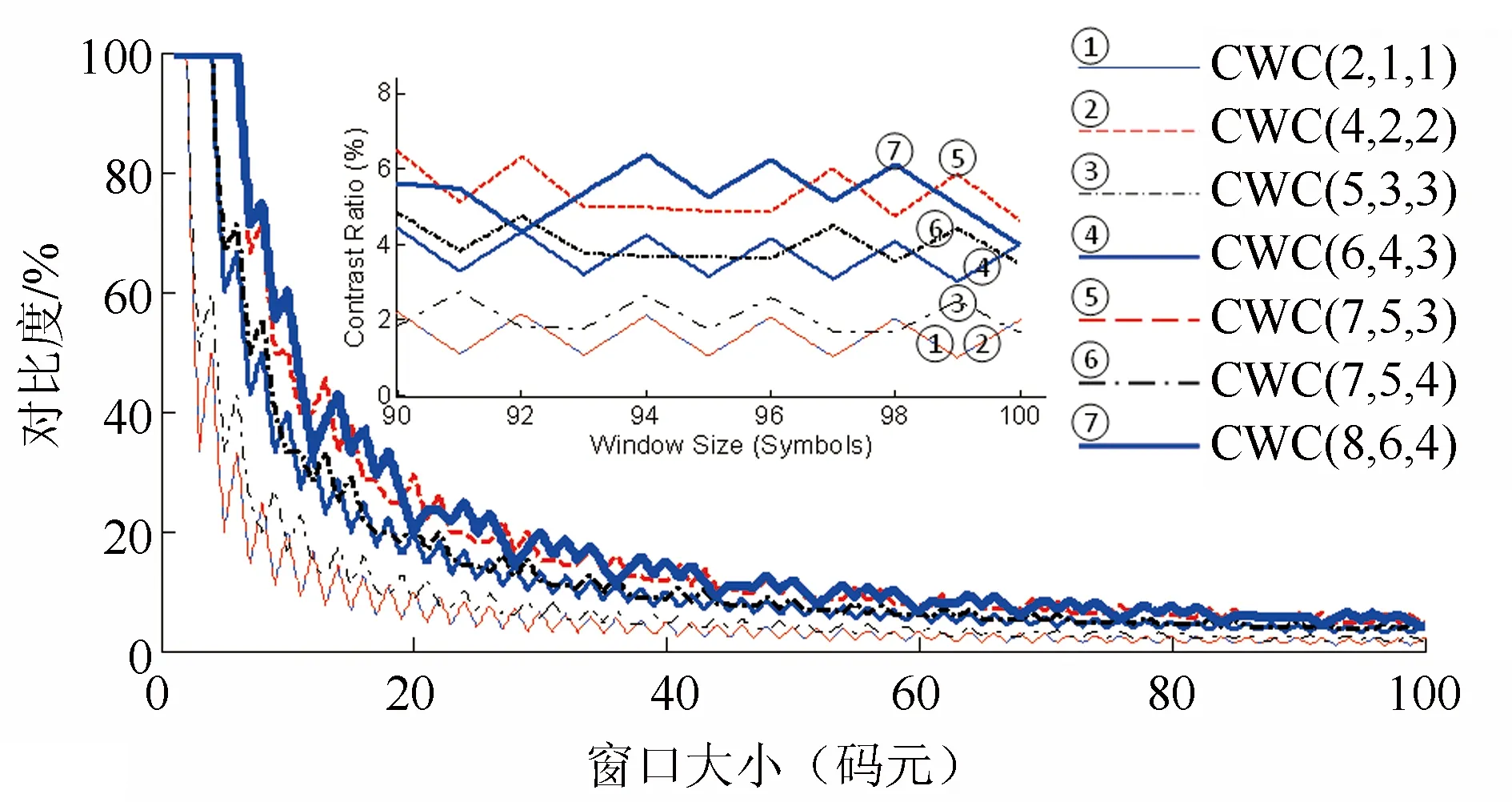
图3 不同常权编码的最优编码表的CR曲线对比

3 结 语

常权编码是一种能有效抑制光学相机通信系统中LED闪烁的技术。在给定的编码条件下，基于跳的算法可以快速有效地找到闪烁抑制的最优编码表。研究表明，编码效率随码字长度的增加而增加，而闪烁抑制性能随码字长度的增加而降低，在实际应用中要根据系统可以支撑的码率以闪烁抑制优先来进行合理选择。对于同一码字长度和编码效率，权重越大的常权编码能更好地抑制闪烁。

：

[1] N. Saha, M. S. Ifthekhar, N. T. Le, and Y. M. Jang, “Survey on Optical Camera Communications: Challenges and Opportunities,” IET Optoelectronics, 2015, 9(5):172-183.

[2] R. D. Roberts, “Undersampled Frequency Shift On-Off Keying (UFSOOK) for Camera Communications (Camcom),” IEEE Wireless & Optical Communication Conference, 2013:645-648.

[3] P. Luo, M. Zhang, Z. Ghassemlooy, H. L. Minh, H.-M. Tsai, X. Tang, L. C. Png, and D. Han, “Experimental Demonstration of RGB LED-Based Optical Camera Communications,” IEEE Photonics Journal, 2015, 7(5)：1-6.

[4] C. Danakis, M. Afgani, G. Povey, I. Underwood, and H. Haas, “Using a CMOS Camera Sensor for Visible Light Communication,” IEEE Workshop on Optical Wireless Communications, 2012:1244-1248.

[5] T. Nguyen, C. H. Hong, N. T. Le, and Y. M. Jang, “High-Speed Asynchronous Optical Camera Communication Using LED and Rolling Shutter Camera,” IEEE International Conference on Ubiquitous and Future Networks, 2015：214-219.

[6] A. E. Brouwer, J. B. Shearer, N. J. A. Sloane, and W. D. Smith, “A New Table of Constant Weight Codes,” IEEE Transaction on Information Theory, 1990, 36(6):1334-1380.

7.D. H. Smith, L. A. Hughes, and S. Perkins, “A New Table of Constant Weight Codes of Length Greater Than 28,” Electronic Journal of Combinatorics, 2006, 13(1): 193-201.