基于公共余数最优估计的多通道干涉SAR高程重建方法
2018-05-28,,*,,,,
,,*,,,,
1. 长沙理工大学 电气与信息工程学院,长沙 410004 2. 长沙理工大学 交通运输工程学院,长沙 410004 3. 北京空间飞行器总体设计部,北京 100094
星载分布式干涉合成孔径雷达(Synthetic Aperture Radar Interferometry,InSAR)系统是将卫星编队技术与星载SAR技术相结合的雷达系统。它通过多颗卫星编队飞行、协同工作来进行地面高程测量。相对于其他地面高程测量方式和其他InSAR系统,星载分布式InSAR系统具有自己独特的优点。它是以合成孔径雷达复数据提取的相位信息为信息源获取地表的三维信息和变化信息的一项技术[1-3],可以在全天时、全天候条件下获取宽测绘范围的地面三维高分辨图像,在地形快速测绘与更新方面具有重要应用价值。而多通道InSAR测量技术(多基线InSAR测量技术[4]和多频率InSAR测量技术[5]统称为多通道InSAR测量技术)则是在传统单基线InSAR测量技术基础上发展起来的一种新型测绘技术,它可以有效克服或减少复杂地形及较大噪声干扰的影响,提高InSAR对复杂地形的测量精度,尤其是地形陡变区域的高程重建作用明显,是近年来的研究热点,也是未来发展的方向[6-7]。
目前,利用多通道InSAR数据进行高程重建的技术得到了发展,其中非统计信号处理的方法引起了人们很大的兴趣。特别是基于中国余数定理的方法,Xu等提出了包括中国余数定理(Chinese Remainder Theorem,CRT)法、线性组合法和平面投影法的三种多通道干涉SAR相位解缠方法[8]。Thompson等提出了一种基于级联迭代法的多基线干涉SAR相位解缠方法,该方法不仅利用了短基线相位解缠的可靠性,还保持了长基线高程测量的高精度性[9]。Pascaziop等提出了基于最大似然估计(ML)的高程重建方法[10]。然后基于最大后验概率(MAP)估计的方法被提了出来[11],该方法利用马尔可夫随机场统计分布模型来描述目标高程的先验分布,通过估计每个像素对应的超参数,实现对目标高程的最大后验概率估计。夏香根等提出了一种基于搜索算法的鲁棒性中国余数定理,并利用了对余数的差分处理过程[12]。黄文杰等提出了一种闭合形式的鲁棒性中国余数定理,其原理是通过合理地选择参考余数和对余数进行差分操作以提高算法的鲁棒性[13]。袁志辉首次将闭合形式的鲁棒性中国余数定理应用到多通道干涉SAR高程重建中来[14]。试验结果表明,基于MAP高程重建法比ML高程重建法的性能好很多,但是由于MAP高程重建法需要重复迭代估计每个像素对应的超参数和高程值,因而存在计算时间非常长的缺点,ML高程重建法则不存在这样的问题。而闭合形式的鲁棒性中国余数定理法相比于最大似然估计法、最大后验概率估计法在高程精度重建、计算效率和鲁棒性上均有所提高,但在计算效率方面还不是很理想。本文提出基于公共余数最优估计的多通道干涉SAR的高程重建方法,并与ML高程重建法、MAP高程重建法及鲁棒性CRT高程重建法进行了对比分析。试验数据处理结果表明,该方法使高程重建的计算效率有了显著提升。
1 公共余数最优估计的多通道干涉SAR高程重建方法
1.1 重建原理
(1)
式中:l为各个干涉通道的序号;h(p)为位置p上的像素所对应的高程值;hl为第l个干涉通道对应的高度模糊数;wl(p)为去相关相位噪声;〈·〉2π为“模2π”操作。
定义模糊数:
nl≜⎣h(p)/hl」
(2)
式中:⎣·」表示向下取整。在无噪声情况下,将式(2)代入式(1)可得:
π·nl
(3)
又令
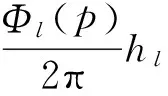
(4)
将式(4)代入式(3)并进行变换,可得形如式(5)的同余方程组:
(5)
又令
Γl=hl/M, 1≤l≤L(6)
式中:M为系统设计的、事先已知的一个实数归一化因子,它可以使所有的Γl均为正整数且互素。那么式(5)可以写成如下形式:
(7)
且有如下定义:
Γ≜Γ1Γ2…ΓL(8)
γL≜Γ1…Γl-1Γl+1…ΓL=Γ/Γl(9)
由中国余数定理可知,在0~MΓ的范围内,h(p)有唯一解。为了避免式(7)求出来的余数rl出现负数(这是由于一般的缠绕干涉相位都限定在-π~π之间),在应用中国余数定理之前,需把缠绕干涉相位Φl转换到0,2π,这样就可以按照第1.2节的算法步骤对目标像素的高程进行求解了。
1.2 重建流程
通过前面对基于公共余数最优估计的多通道干涉SAR高程重建原理的分析,本节给出了高程重建的具体流程,直接利用最优估计方法得出公共余数的闭合解,再计算高程重建值。图1给出了本文高程重建算法流程。

图1 基于公共余数最优估计的多通道干涉SAR高程重建流程Fig.1 The flow chart of the elevation reconstructionof multichannel InSAR by optimalestimation of remainder
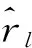
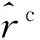
(11)
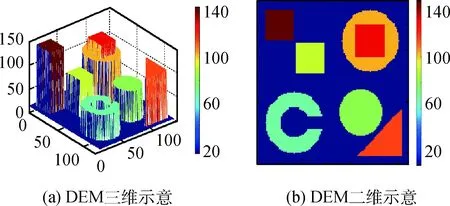
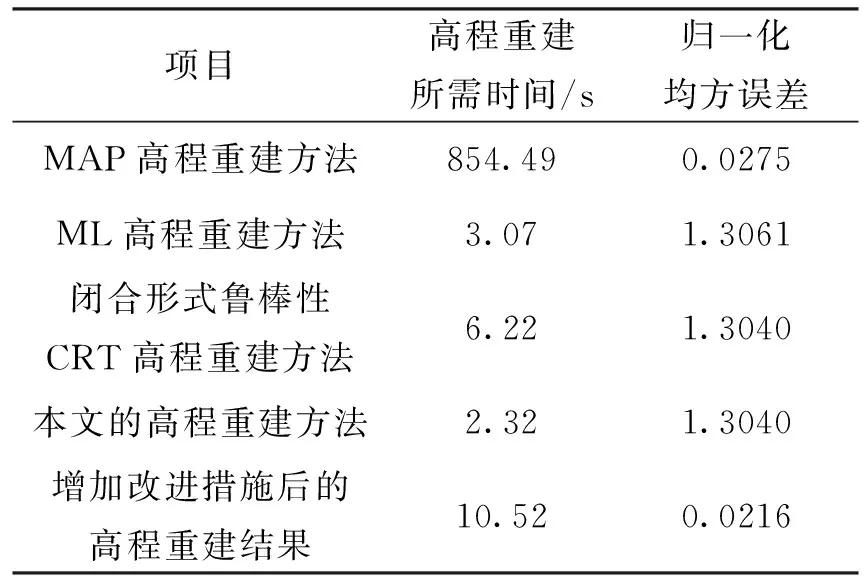
对于实数0≤m d(m,nM)≜m-n-k0M(12) k0可以通过下式计算得到: (13) 3)选择参考余数的索引号: (14) ,l=2,3,…,L (15) Γl,l=2,3,…,L (16) γ1 (17) (18) 8)求出h的估计值: Δrl(19) 定义每一个像素对应各个干涉通道的干涉相位的模糊数所组成的矢量为模糊矢量,而由所有高度模糊矢量相同的像素所组成的集合称为模糊集。对于一幅给定场景的SAR图像,特别是一些城市地区或者比较平坦的地区,上面有很多像素都具有相似的高程,因而基本上处在相同的模糊集里。在实际的地形中,并不是所有的模糊矢量都会出现,只不过由于噪声的影响而使某些本不存在的模糊矢量出现了。联合信息处理及加权均值滤波可以用来改善最终的高程重建结果。 1)使用常用的直方图统计法来计算具有相同模糊矢量的像素的个数,各像素对应的模糊矢量已经事先求出。 2)对于每一个模糊集,如果对应的像素个数高于某一事先设定的门限值,并且其高程值并不是明显特别高,则保留该模糊集;否则,该模糊集内的像素被认为是高程误差非常大的坏点像素,将其合并到一个新的模糊集里面去。 3)最后,利用如下的加权均值滤波器对所有的坏点像素高程值进行更新: (21) 式中:p′为与像素p相邻的像素;μp′为设定的像素p′对应的加权系数,一般可用对应像素的相干系数代替。 为了验证本文算法的有效性,利用仿真数据进行了相关试验。如图2所示的一个128×128的地形高程场景,其最小高程为16 m,最大高程为144 m。该场景既有平坦的区域,也有边沿陡峭的区域,相邻两点的最大高程差为128 m。这里仿真了3个干涉通道的干涉条纹图,它们对应的高度模糊数分别为21.4 m,32.1 m,53.5 m,都小于最大高程差。假设3幅干涉条纹图的相关系数都是0.95。 图2 仿真的地形参考高程Fig.2 Reference height profile 项目高程重建所需时间/s归一化均方误差MAP高程重建方法854.490.0275ML高程重建方法3.071.3061闭合形式鲁棒性CRT高程重建方法6.221.3040本文的高程重建方法2.321.3040增加改进措施后的高程重建结果10.520.0216 仿真结果表明,本文的高程重建方法和ML高程重建方法及闭合形式鲁棒性CRT高程重建方法的性能是十分相似的。本文方法在精度和时间上都要优先于ML高程重建方法。在保持精度不变的情况下,本文的高程重建方法在效率上总是优先于闭合形式鲁棒性CRT高程重建方法,比其提高数倍。当场景较大时,优势将更加明显。虽然基于MAP估计法的高程重建结果比本文方法要好一些,但是它们在计算效率上的性能对比则不可同日而语。图3(h)是在3(g)的基础上增加改进措施的高程重建结果,其归一化均方误差为0.021 6,效果还要优先基于MAP的高程重建方法,且所耗时间比其缩短了近两个数量级,由此可见本文方法的优越性。 本文针对多通道干涉SAR高程重建方法的计算效率较低的问题,提出了基于公共余数最优估计的多通道干涉SAR高程重建算法,利用最优估计方法直接计算得出公共余数的最优估计值,进而求解出高程重建值。仿真数据验证结果表明,本文方法大大提高了高程重建的执行效率。 参考文献(References) [1] BAMLER R, HARTL P. Synthetic aperture radar inter-ferometry[J]. Inverse Problems, 1998, 14(4): R1-R54. [2] ROSEN P, HENSLEY S, JOUGHIN I. et al. Synthetic aperture radar interferometry[J]. Proceedings of the IEEE, 2000, 88(3): 333-382. [3] RICHARDS M A.A beginner′s guide to interferometric SAR concepts and signal processing[J]. IEEE Aerospace and Electronic Systems Magazine, 2007, 22(8): 5-29. [4] FERRETTI A, PRATI C, ROCCA F. Multibaseline InSAR DEM reconstruction: the wavelet approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(2): 705-715. [5] PASCAZIO V, SCHIRINZI G. SCHIRINZI. Estimation of terrain elevation by multifrequency interferometric wide band SAR data[J]. IEEE Signal Processing Letters, 2001, 8(1): 7-9. [6] KRIEGER G, HAJNSEK I, PAPATHANASSIOU K P, et al. Interferometric synthetic aperture radar (SAR) missions employing formation flying[J]. Proceedings of the IEEE, 2010, 98(5): 816-843. [7] 梁健,张润宁,包敏凤.天基视频SAR系统设计及成像算法研究[J].中国空间科学技术,2016,36(6):22-28. LIANG J,ZHANG R N,BAO M F.Research on spaceborne video SAR system design and image formation algorithm[J].Chinese Space Science and Technology,2016,36(6):22-28(in Chinese). [8] XU W, CHANG C, et al. Phase-unwrapping of SAR interferogram with multi-frequency or multi-baseline[C]. IGARSS, Pasadena,1994: 730-732. [9] THOMPSON D R,ROBERTSON A E. Multibaseline interferometry SAR for iterative height estimation[C].IGASS,Hamburg,Germany,Jan.,1999:251-253. [10] PASCAZIO V, SCHIRINZI G. Multifrequency InSAR height reconstruction through maximum likelihood estimation of local planes parameters[J].IEEE Transactions on Image Processing ,2002,11(12):1478-1489. [11] FERRAIUOLO G, PASCAZIO V, SCHIRINZI G. Maxi-mum a posteriori estimation of height profiles in InSAR imaging[J].IEEE Geoscience and Remote Sensing Letters,2004,1(2):6. [12] XIA X G,WANG G.Phase unwrapping and a robust Chinese remainder theorem[J]. IEEE Signal Processing Letters, 2007, 14: 247-250. [13] WANG W, XIA X G. A closed-form robust Chinese remainder theorem and its performance analysis[J]. IEEE Transactions on Signal Processing, 2010, 58: 5655-5666. [14] YUAN Z H, DENG Y K, LI F. et al. Multichannel InSAR DEM reconstruction through improved closed-form robust Chinese remainder theorem[J].IEEE Journals & Magazines,2013,10(6):1314-1318. [15] FERRAIUOLO G, MEGLIO F, PASCAZIO V,et al. DEM teconstruction accuracy in multichannel SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 191-201. [16] LI X P, WANG W J,WANG W, et al. Optimal estimates of common remainder for the robust Chinese remainder theorem[J].Commun.Nonlinear Sci.Numer.Simulat.,2014,19(7):2373-2381.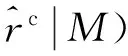
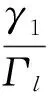
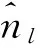
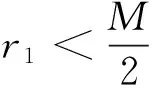
1.3 改进措施
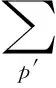
2 数据验证及分析
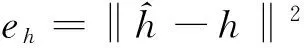
3 结束语
