车用复合电源参数与能量管理策略优化方法
2018-05-28杨大鹏张幽彤
杨大鹏,张幽彤*
(北京理工大学清洁车辆实验室,北京 100081)
前言
动力电池作为纯电动汽车的重要储能部件,其性能备受关注。目前任何一种单一能量源难以满足电动汽车对能量密度和功率密度的双重需求。相比之下,将高功率密度、长寿命的超级电容与高能量密度的锂离子动力电池相结合构成车用复合电源系统,能够有效提高系统功率密度[1,2],同时可以缓解大功率放电对锂离子电池寿命的影响[3]。
复合电源系统部件参数匹配和能量管理策略是重点研究方向。文献[4-7]分别考虑工况、成本等因素,对车用复合电源系统进行优化设计。复合电源系统能量管理策略主要包括基于规则的能量管理策略[8]、基于离线优化结果的能量管理策略[9]、模型预测算法和随机动态规划算法能量管理策略[10]。
目前相关的研究多数是在完成参数匹配优化后进行策略设计,而实际这两个步骤有很强的耦合关系,二者应联合展开[11]。本文以半主动式复合电源为研究对象,以复合电源动力电池全寿命行驶里程和整车耗电量为优化目标,提出基于NSGA-II的参数与能量管理策略联合优化方法,同时对复合电源重要参数和能量管理策略参数进行优化,在约束范围内得出优化解集,进而根据实际设计需求对匹配结果进行优选。
1 复合电源初步配置
1.1 基本构型与参数配置
复合电源系统依据动力电池、超级电容及 DC/DC变换器的拓扑关系分为四类:被动式(包括改进型被动式)、半主动式、主动式[12]和混合式[13]。本文选取如图1所示半主动式构型。系统主要由动力电池组、超级电容组、双向 DC/DC变换器构成,动力电池组直接与动力母线相连,双向DC/DC变换器的两端分别与超级电容组和动力母线相连。

图1 半主动式复合电源系统
初步配置的车辆行驶能量Eb主要由动力电池提供,应当满足续航里程需求,如式(1)所示:

式中:Eh为百公里耗电量;S为续航里程,DOD为电池组放电深度。
复合电源系统输出功率 Pe应满足车辆行驶过程中的功率需求如式(2)所示:

式中:ηt为传动效率;m为整车质量;f为滚动阻力系数;CD为风阻系数;A为迎风面积;α为坡角;δ为旋转质量系数。
考虑整车加速和爬坡两种工况进行计算,将如表1所示某纯电动汽车作为研究原型,带入式(1)、(2)获得该车所需能量Eb≥41.4kW·h,最大输出功率Pmax=52.3kW。

表1 某纯电动汽车参数表
1.2 复合电源系统能量管理策略
电源系统的参数与能量管理策略联合优化前,需先制定能量管理策略框架。依据文献[14]制定基于规则的复合电源能量管理策略,其优化参数集相对较小、优化复杂度适中,且便于策略的实现,控制逻辑如表2所示。
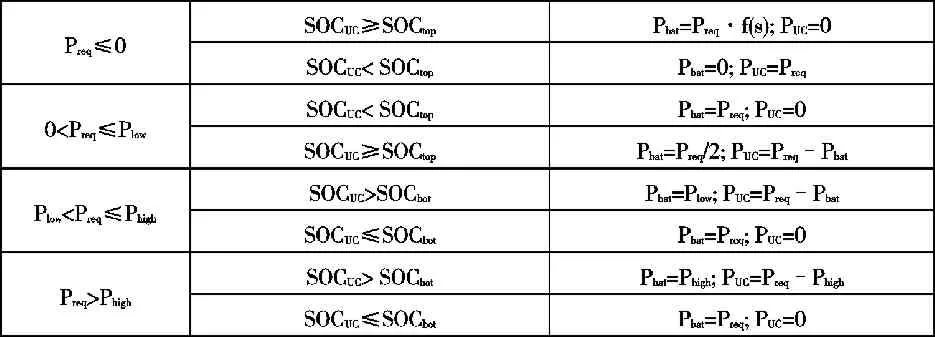
表2 控制逻辑表
表2中,Preq为母线需求功率;Pbat和PUC分别为动力电池和超级电容所分配的功率;SOCUC为超级电容荷电状态;SOCtop和SOCbot为超级电容和荷电状态的边界,通常取0.95和0.4;Plow和Phigh为待优化的门限值。需要注意,当Preq<0,即再生制动工况下,优先使用超级电容组进行能量回收,在电池功率回收上加入一阶低通滤波f(s)以防止发生振荡。
2 参数匹配目标
在确定复合电源构型和能量管理逻辑的前提下,需要确定的复合电源主要参数有:动力电池串并联数nbats、nbatp;超级电容组串并联数nucs、nucp;能量管理策略参数Plow和Phigh。本文用于匹配优化的动力电池单体额定电压3.2V,额定容量5Ah;超级电容额定电压2.7V,额定电容量为3000F。
由于动力电池组和超级电容组的主要参数是决策变量,在相同策略下,不同nbats、nbatp、nucs、nucp组合,Plow和Phigh是不同的。因此,为了保证能量管理策略的通用性,对 Plow和Phigh进行归一化处理,在能量管理策略中引入归一化功率概念CP,1CP代表动力电池以1C倍率放电时所对应的功率。以CPlow=Plow/1CP和CPhigh=Phigh/1CP作为决策参数,使优化策略结果具有较强的通用性。
综上所述,本文进行复合电源参数和能量管理联合优化的任务是找到参数集X=[nbats, nbatp, nucs, nucp, CPlow, CPhigh],使得多性能指标达到最优。本文以复合电源中磷酸铁锂电池全寿命行驶里程和整车能耗经济性作为优化指标,利用NSGA-II方法进行寻优,求出最优参数集合。
3 基于NSGA-II的多目标优化
3.1 优化目标
为了获得电池全寿命行驶里程和整车能耗经济性综合优化结果,对复合电源系统参数和能量管理策略关键参数进行多目标优化。根据磷酸铁锂动力电池衰退特征和电池容量衰退与充放电倍率、累计转移容量以及温度之间的关系[3],将电池全寿命内(即动力电池容量损耗达到20%)的总行驶里程作为衡量动力电池使用寿命的表征参数,以百公里能耗表征整车能耗经济性。
3.2 驾驶-充电循环工况分析
磷酸铁锂动力电池使用寿命与其工作区间存在一定关系[15],不同日均行驶里程对应的动力电池工作区间有所差别。依据 NHTS对家庭用车日常驾驶距离进行统计分析[16]结果如图2所示。超过90%的驾驶者日均行驶里程低于75英里,即121km。因此,本文将日均行驶里程设定为121km进行优化。

图2 日常驾驶距离统计
本文将UDDS(Urban Dynamometer Driving Schedule)工况与日常充电工况相结合,构成驾驶-充电循环工况,在该工况中动力电池以SOC为0.9起始,循环运行UDDS工况,直至达到设定的日均行驶里程,然后以通用电动汽车充电桩的交流电220V、5.5kW进行充电,直至电池SOC达到0.9方可停止充电。
3.3 多目标优化
3.1.1 优化模型
优化指标是电池全寿命范围内的总行驶里程Stotal和百公里电耗量Eh,优化模型如式(3):

式中:[xL,xH]为决策变量x的上限和下限;hi(x)为决策变量x满足的l维等式约束;gj(x)为决策变量x满足的k维不等式约束。Stotal(x)的负号是将最大化问题转化为最小化问题。
3.3.2 适应度模型
(1)动力电池全寿命行驶里程
本文基于John Wang[17]、罗玉涛等[18]的磷酸铁锂电池行驶工况寿命模型,在驾驶-充电循环工况下,当放电倍率小于10时,容量损失由式(4)表示:

式中:QN为容量损失百分数;N为已进行的驾驶-充电循环工况次数;n(t)为实时放电倍率;tc为一个驾驶-充电循环工况的总时长;I1为电池1C放电电流。
利用MATLAB/Simulink软件建立如图3所示带有复合电源系统的整车动力模型,用以得到动力电池全寿命行驶里程。
该模型输入驾驶-充电循环工况,利用能量管理策略将功率总线上的功率需求分配给动力电池及双向 DC/DC和超级电容组,电池寿命模型嵌入于动力电池模型中,当电池容量衰减至初始容量状态的80%时,触发终止循环工况信号,此时系统总行驶里程即为电池全寿命行驶里程Stotal。同时基于表1整车参数,仿真得原车在日均行驶里程121km时的全寿命总行驶里程为6.0万公里,百公里电耗17.35kW·h。

图3 带复合电源的整车模型
(2)百公里耗电量
不同的复合电源参数和能量管理策略,将直接影响复合电源系统的能耗水平,本文以式(5)表征百公里耗电量Eh:

式中Edis为动力电池全寿命周期内累计放电能量;N为动力电池所进行的循环次数;(tsi,tci)为第i个循环动力电池放电时间;Pdis为动力电池放电功率。式(5)中计算参数由图3所示整车模型获得。
3.4 NSGA-II多目标优化过程
针对复合电源系统参数与能量管理策略优化问题的多目标、多变量、高度耦合的特点,本文采用带受控精英策略的非支配排序遗传算法(Nondominated Sorting Genetic Algori-thm II,NSGA-II)进行多目标优化求解,以前述决策变量X=[nbats, nbatp, nucs, nucp, CPlow, CPhigh]为个体构建初始种群,决策变量范围如表3所示。

表3 决策变量范围

图4 NSGA-II优化流程
图3整车模型作为适应度模型计算动力电池全寿命行驶里程和百公里电耗量两个指标的结果并输出,受控精英策略将父代种群与子代种群进行融合,计算拥挤距离进行竞争排序,共同产生下一代种群,将距离相近的个体进行适当剔除,有利于保证每一代种群的多样性[19]。 如图4所示为NSGA-II的优化流程图,其参数配置如表4所示。
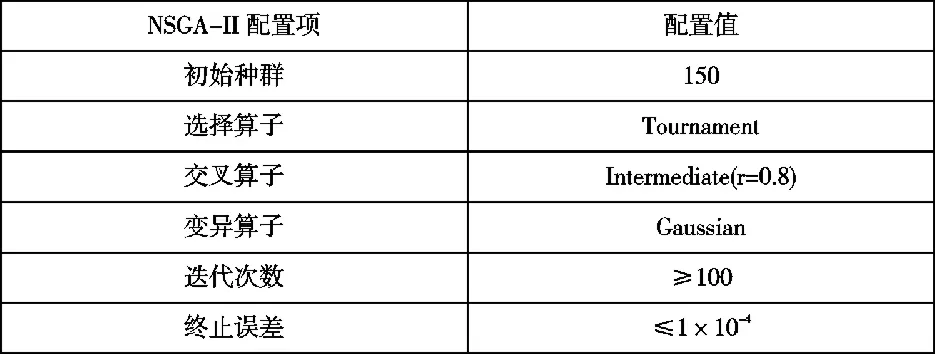
表4 NSGA-II参数配置表
3.5 优化结果分析
本文采用NSGA-II方法的结果是一系列非支配最优解,构成Pareto解集。这些解构成的Pareto前沿如图5所示。

图5 日均行驶121km下优化结果的Pareto前沿
Pareto前沿上每个解表示一个可行备选方案,其内容包含前述决策变量X= [nbats, nbatp, nucs, nucp, CPlow, CPhigh]。Pareto解集中每个备选方案能不同程度达到优化效果,方案之间是非支配的关系,总行驶里程与百公里电耗两个指标存在竞争,例如图中A与B两点,A的百公里电耗指标优于B,而总行驶里程指标劣于 B。Pareto解集的意义在于,其中任意一个解都具有非劣性:若设计者从非Pareto解集中选取方案M,则Pareto解集中存在着至少一个解方案M’,使得M’至少一项指标优于M,而其他指标不劣于M。
本文优化目的是要尽可能延长总行驶里程、降低百公里电耗,即向图5中右下方区域靠近。二者无法同时达到最优,一个指标的优化需要以另一个指标相对劣化为代价。这是由于提高总续航里程倾向于延长电池的使用寿命,对动力电池的限制较大,相应引起的超级电容和DC/DC承担更多负荷,从而增加电耗量。
4 多目标优选决策
通过NSGA-II方法获得的的Pareto解集包含多个备选方案如图6所示,各备选方案之间为非支配关系,因此在优化指标空间内(总行驶里程、百公里电耗)不能直接比较优劣,本文采用线性加权法建立式(6)所示多目标决策优选函数,处理前文所得Pareto解集。
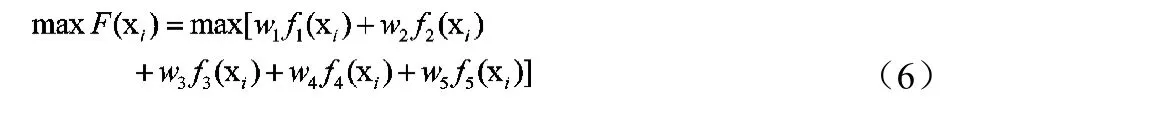
式中:xi为备选方案i对应的决策变量集[nbats, nbatp, nucs,nucp, CPlow, CPhigh],fj(xi)为依据 xi所计算出的 j项指标(j=1,2,…,5)归一化表达值——f1(xi)为比能量,f2(xi)为比功率,f3(xi)为能量密度,f4(xi)为比能量,f5(xi)为初始成本,wj为对应权重。

图6 日均行驶121km的Pareto解集
式(6)中归一化值选取式(7)或式(8)计算获得,选取原则依据文献[20]的归一化方法:设共有m个备选方案,第i个方案的第j项指标(i=1,2,…,m; j=1,2,…5)实际值为v(i, j),对于追求最大化的指标应用式(7),对于追求最小化的指标应用式(8),计算其归一化值fj(xi):

基于图6中Pareto解集的各个方案参数,以式(9)所示变异系数法[20]求出客观权重向量w’=[0.232, 0.169, 0.233, 0.168,0.198]。依据文献[21]、[22]衡量各指标相对重要程度,提出主观权重向量w”=[0.268, 0.179, 0.202, 0.134, 0.217]。采用组合赋权法[23],基于各备选方案每项指标的归一化数据,依据偏离度最小模型,用式(10)将主、客观权重进行组合,组合结果能够充分体现主客观权重,最终解得本文所需权重向量w=[0.250, 0.174, 0.217, 0.152, 0.207]。

式中:∂j为j指标的变异系数,Gj为j指标的均方差。
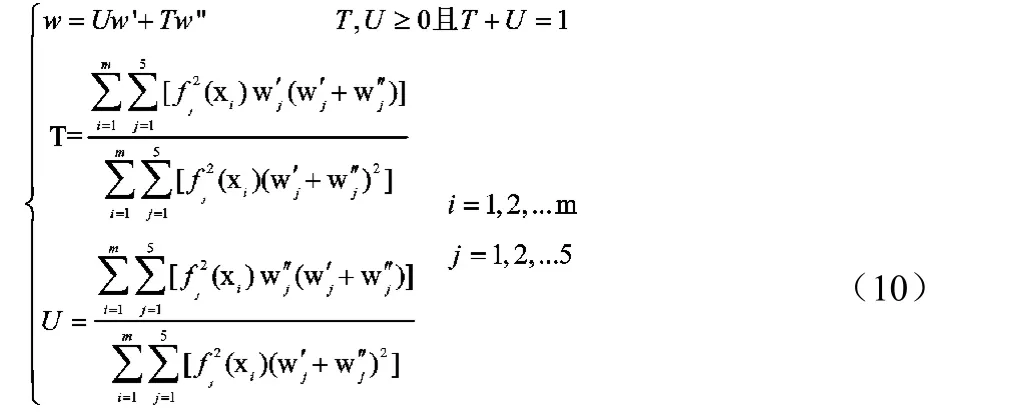
图6中CD段、FG段斜率较小,在该区间内各个解的百公里耗电量相近,即以较小的油耗代价可较大的提升总行驶里程;AC段、DF段斜率较大,即两个指标竞争关系明显。表5列举图6中方案A~G参数及对应优选目标函数值。选取优选函数值最高的方案E作为最终优化结果。
前文得到原车日均行驶 121km时的全寿命总行驶里程为6.0万公里,百公里电耗17.35kW·h。对比本文所得优化结果,该方案位于日均行驶121km时的Pareto前沿上,总行驶里程延长35%,百公里能耗降低14.0%。

表5 备选方案参数及优选函数值
5 结论
1)提出一种车用复合电源参数、能量管理策略联合匹配方法。以整车需求为约束,以电池全寿命行驶里程、百公里电耗为优化指标,采用NSGA-II方法进行多目标优化,得到满足条件的Pareto最优解集。
2)Pareto最优解集所得到的方案,均能达到优化效果,不同方案对总行驶里程和百公里耗电量的优化程度有所不同,这里两个指标相互竞争。
3)基于 Pareto解集中方案通过线性加权法建立优选函数,其中权重由组合赋权法综合主客观权重向量得到。在Pareto解集中选取优选函数值最高的方案作为最终优化结果,该方案在日均行驶121km的UDDS工况下,电池全寿命行驶里程提高35.0%,百公里能耗降低14.0%。
参考文献
[1] Gu L,Wang Y,Fang Y,et al.Performance characteristics of superca-pacitor electrodes made of silicon carbide nanowires grown on carbon fabric[J]. Journal of Power Sources, 2013,243:648-653.
[2] Lu S, Corzine K A, Ferdowsi M. A New Battery/Ultracapacitor Energy Storage System Design and Its Motor Drive Integration for Hybrid Electric Vehicles[J]. IEEE Transactions on Vehicular Tech-nology, 2007,56(4):1516-1523.
[3] 高飞,杨凯,惠东,等.储能用磷酸铁锂电池循环寿命的能量分析[J].中国电机工程学报, 2013,33(05):41-45.
[4] Park J, Raju B, Emadi A. Effects of an Ultra-Capacitor and Battery Energy Storage System in a Hybrid Electric Vehicle[C]// Future Transportation Technology Conference & Exposition. 2005.
[5] 于远彬,王庆年,王加雪,等.混合动力汽车车载复合电源参数匹配及其优化[J].吉林大学学报(工学版), 2008(04):764-768.
[6] 闵海涛,刘杰,于远彬,等.混合动力汽车复合电源参数优化与试验研究[J].汽车工程, 2011(12):1078-1083.
[7] 李勇,江浩斌,徐兴,等.采用 NSGA-Ⅱ算法的纯电动汽车复合电源参数匹配及优化[J].科学技术与工程, 2017(27):101-109.
[8] Breban S, Mollet F, Saudemont C, et al. Embedded electric power system with fuzzy-logic supervision for vehicular applications[C]//International Conference on Optimization of Electrical and Electro-nic Equipment. IEEE, 2012:1575-1579.
[9] 宋传学,周放,肖峰.基于动态规划的复合电源能量管理优化[J]. 吉林大学学报(工学版), 2017,47(1):8-14.
[10] Song Z, Hofmann H, Li J, et al. Energy management strategies comparison for electric vehicles with hybrid energy storage system[J]. Applied Energy, 2014,134(C):321-331.
[11] Ebbesen S, Nitz C D, Guzzella L. Particle swarm optimisation for hybrid electric drive-train sizing[J]. International Journal of Vehicle Design, 2012,52(2-4):181-199.
[12] 王琪,孙玉坤,黄永红.不同结构混合动力汽车用复合电源的比较[J]. 江苏大学学报(自然科学版), 2014,35(5):578-582.
[13] 王斌,徐俊,曹秉刚,等.升压型电池-超级电容复合电源的自适应滑模控制[J]. 西安交通大学学报, 2016(10):36-41.
[14] 朱福顺,何洪文,何银.基于硬件在环仿真的复合电源能量管理研究[J]. 机械设计与制造, 2013(01):119-121.
[15] 杨代铭,李相俊,陆超,等.磷酸铁锂电池工作区间的优化及应用[J].电器与能效管理技术, 2014(10):60-66.
[16] National Household Travel Survey[EB/OL]. http://nhts.ornl.gov/.
[17] Jang W, Chen Z, Bao W, et al. Cycle-life model for graphite-LiFe PO4 cells[J]. Journal of Power Sources, 2011,196(8):3942- 3948.
[18] 罗玉涛,王峰,喻皓,等.基于行驶工况的磷酸铁锂电池寿命模型研究[J].汽车工程, 2015(08):881-885.
[19] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation, 2002,6(2):182-197.
[20] 张荣,刘思峰,刘斌.基于离差最大化客观赋权法的一般性算法[J].统计与决策, 2007(24):29-31.
[21] 林程,孟祥峰,王震坡,等.电动汽车用动力电池综合性能评价方法的研究[J].高技术通讯, 2006,16(9):929-933.
[22] 让松.新能源汽车用动力电池综合评价体系简介[J].汽车电器,2015(06):62-64.
[23] 王中兴,张绍林,刘雁.基于主客观加权属性值一致化的组合赋权法[J].广西科学, 2007(03):247-249.
