一种基于物理熵源的扩频随机序列的产生及其扩频特性分析

刘雪元，郎百和，冯玉玲，姚治海，王晓茜

（1.长春理工大学 电子信息工程学院，长春 130022；2.长春理工大学 理学院，长春 130022）

扩频通信技术利用扩展频谱带宽的方式有效地提高了系统的可靠性，因其良好的抗干扰性能已广泛应用于军事和民用通信中［1-3］。扩频通信系统性能的优劣主要取决于扩频序列的性质。香农的信息理论指出，在平均功率受限的信道上加入高斯白噪声干扰情况后，具有白噪声统计性质的信号是实现有效和可靠通信的最佳信号［4］。传统扩频通信一般采用伪随机序列作为扩频码［5］，如m序列和Gold序列等，但它们存在周期性且数量有限、线性复杂度低、保密性差等不足［6］。混沌序列因其对初值的敏感性、码组丰富和非周期性等特性，常常被用作扩频码。2003年，柏逢明等［7］人提出利用超混沌序列作为扩频序列，并且给出了超混沌序列发生器的算法和硬件实现电路。2004年，于银辉等人［8］以改进型的Logisti-Map为基础，采用迭代法生成混沌序列。通过对混沌CDMA性能的分析，证明改进后混沌序列适合做扩频码。2013年，俞斌等人［9］提出了一种组合式混沌映射模型，生成了一种新的混沌扩频序列。对其特性分析表明，该序列与原有混沌序列相比具有更好的均衡性和保密性。

近些年来，采用宽带混沌信号［10］作为物理熵源获取高速的真随机数成为研究热点，并被广泛应用于Gb/s量级物理随机数的产生［11，12］。物理随机数是由物理熵源经过后续处理产生的，相比于传统伪随机数及混沌伪随机序列，具有不可预测性、更好的相关性和序列集合的正交性，有望成为扩频通信系统中理想的扩频码。本文利用数值模拟的方式对半导体激光器进行调制从而获得混沌序列，通过对混沌序列二值化、提取最低有效位及后续处理获得物理随机序列，同时利用NIST软件［13］对该序列进行测试，并对其作为扩频码的性能进行研究，为物理随机序列充当扩频码用于扩频通信打下基础。

1 理论模型

物理随机数发生器一般由三个部分组成：物理熵源、采集部分和后续处理部分。在物理熵源产生过程中，激光器外腔反馈延迟会带来一定的周期性。采样率的高低决定着信号的每个点之间的相关性的高低，采样率越低则序列的相邻点之间的相关性就越低，从而提高随机序列的随机性，但是却降低了随机序列的速率；量化取决于量化的精度，精度越高，量化后每一位对应的二元码位数就越多，从而使得最终生成的随机序列速率增加，但是同时也会降低序列的随机性。因此，必须进行后续处理来优化随机数的性能。

本文采用的理论模型如图1所示。对半导体激光器施加外部扰动获得的混沌光信号作为物理熵源，通过光电转换模块（PD）转换为电信号。采用8bit ADC将电信号转换为二进制序列输出。根据测试结果，从8位并行输出的二进制序列中提取m位，并转换为串行方式输出。最后利用延迟对二进制码进行移位输出，使得输出的二进制码与原来的二进制码不相关。进而对两列不相关的二进制码进行异或（XOR）运算，可以有效地减小初始序列的偏差和自相关系数，最终获得高质量高速的随机数序列。

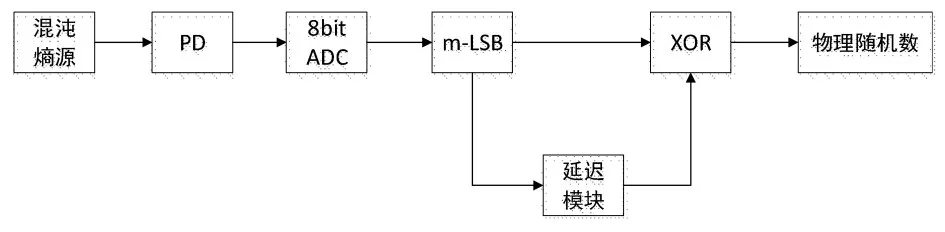
图1 产生随机数的理论模型

产生混沌熵源所用的半导体激光器动力学特性的速率方程［14］如下：

其中，Jth=Nth/τN，Nth=N0+1/（gτP）。SL的部分参数取值如下：α＝5.0，g＝8.4×10-13m3·s-1，N0=1.4×1024m-3，τp=1.927×10-12s，τin＝8.0×10-12s，τN=2.04×10-9s，ε=2.5×10-23m3，P＝1.44，kf=0.1，τ=2.88ns。

2 Simulink平台搭建和仿真结果

本文利用Simulink仿真平台上搭建的系统主要包括混沌信号二值化处理、提取最低有效位和异或处理这几部分，物理随机序列发生系统框图如图2所示。

其中，数据导入模块（From Workspace）可以将Matlab当前工作空间中的变量数据传入Simulink，使编程方式与方框图方式结合起来进行仿真。由From Workspace模块导入的UT.mat文件是一个二维矩阵，第一列是间隔为的10-9时间向量，第二列是统一过数量级后的混沌幅值向量。这里零阶保持器（Zero-Order Hold）模块作为采样保持模型，采样时间设置为1ns，量化器（Quantizer）模块对该输出值进行离散化，量化间隔设为1，将采样输出结果进行四舍五入量化，得到整数值。模数转换模块（Integer to Bit Converter）可以将整数转换为二进制数据，M设为8位即可以转换0-255之间的整数。经过二值化处理将会并行输出长度为8个比特、速率为1Gb/s的二进制数据。

从模数转换器中选取的位数越多，则串行输出随机数的等效速率越高，但是能够通过NIST测试的项数会减小。这里利用Simulink中位提取模块（Extract Bits）实现有效位提取，即从输入信号中选择指定连续位输出。该模块对浮点型数据无效，所以先利用数据转换模块将数据转换成整型。当保留全部8位数据时，信号幅值分布不均匀。当所保留的m-LSBs逐渐减小，幅值分布的均匀性明显有所改善。但是保留位数过少又会降低输出信号等效速率，所以最终保留4位有效位以速率为4Gb/s的二进制序列输出。经过前面两个处理过程，二进制序列以并行方式输出。帧转换（To Frame）模块将样值转换为帧格式，缓存（Buffer）模块可保证并行数据变成串行数据输出。这里使用单位延迟模块（Unit Delay）将二进制序列延迟两个比特位并保持一个采样间隔，对两路不相关的序列进行异或（XOR）运算。

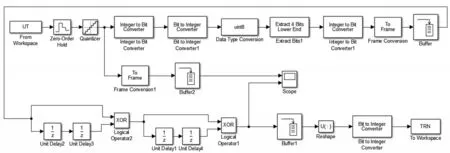
图2 产生随机序列的仿真模型

3 物理随机序列测试和分析

NIST SP 800-22测试软件是美国国家标准技术研究所推出的测试套件，它包含15项统计测试项，用以检验任意长度二进制序列的随机性。其中每项测试都建立在假设的基础上的，设置显著性水平α=0.01，每个检测项均对应一个统计量P-value。采用100组数据进行15项测试，要求每项测试的P-value≥α并且通过率超过0.9601。

香农定理指出：在高斯噪声的干扰下，有限平均功率的信道上，类白噪声统计特性的信号是增加信道可靠通信的最佳信号［4］。基于此，在扩频系统中对扩频码序列特性提出了严格的要求［5］：

（1）良好的均衡性，即保证二进制序列中“0”码和“1”码个数相当。

（2）尖锐的自相关性，即序列的自相关函数接近于δ函数。

（3）尽可能弱的互相关性，可以有效减小不同用户之间的干扰。

基于上述理论，对原始混沌序列和物理随机序列进行性能测试和分析。

3.1 物理随机序列随机特性分析

数量为106混沌信号利用图2所示系统中位提取模块保留m-LSBs后输出的二进制码转换成十进制数，重新返回Matlab工作区编程绘制的统计分布直方图如图3所示。图3给出了图4（a）-（d）分别对应m=8、6、4及保留4-LSBs后再做异或处理的输出结果。横坐标表示量化后的幅值分为2m个单元，纵坐标则表示每个单元幅值的分布概率。从图3可以看出，当保留的位数逐渐减小，幅值分布的均匀性有明显的改善，同时可以通过测试的概率也就越大。

图3 输出信号保留m-LSBs后的统计直方图

保留4-LSBs并经异或处理后，最终输出物理随机序列能够通过NIST软件测试套组的全部15项测试，这表明物理随机序列具有真正的随机性。本文选取其中5项具有代表性的指标，其测试结果如图4所示。这5项测试包括频数测试、累加和测试、长游程测试、频谱测试和近似熵测试。其中，频数测试主要用来检验序列中的1和0个数是否与真正的随机序列近似一致，即各占一半。累加和测试包括前向累加及后项累加，主要看随机游动的最大偏移，随机游动偏移应该在0附近。长游程检测是要判定不同长度游程的数目是否符合理想期望值。频谱测试则是用来检验信号的周期性，显示随机信号之间的偏差程度。最后一项近似熵测试主要看整个序列中所有可能的重叠m-bit模式的频率。

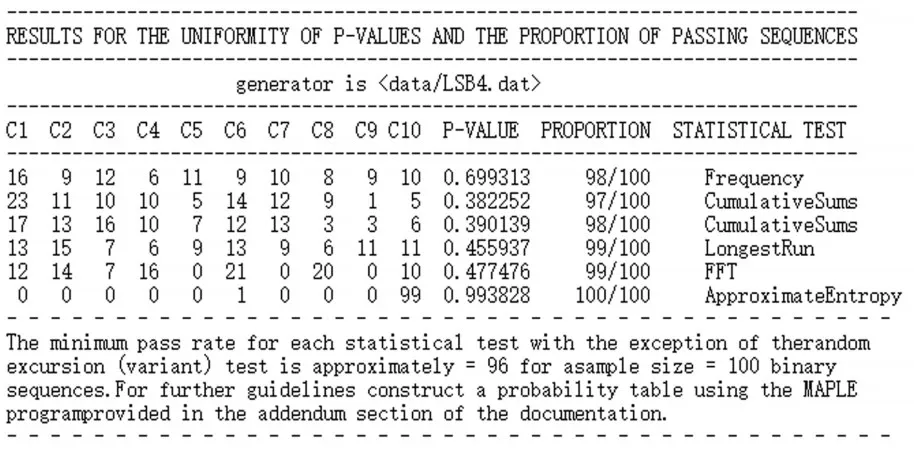
图4 保留4-LSBs测试结果

3.2 物理随机序列平衡特性分析

在直扩系统中，码的平衡性与载波抑制度有密切的关系，扩频码序列不平衡会造成频谱的泄露，将破坏扩频系统保密性、抗干扰和抗侦破能力。扩频序列的平衡性即序列内“0”和“1”的个数平衡，序列的平衡度E［15］表示为：

式中，P，Q分别表示序列中“0”和“1”的个数，N表示序列的总长度。当E为0时，序列达到理想平衡。

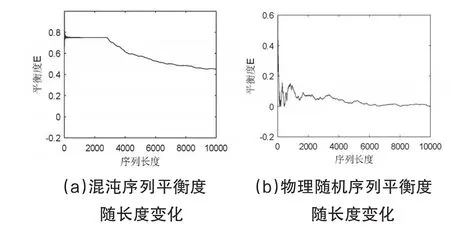
图5 平衡度随序列长度变化曲线

选取长度为10000的混沌序列和物理随机序列进行仿真，两种序列的平衡度随长度变化的曲线如图5所示。由图可知，随着长度的增大，两种序列的平衡性都逐渐趋近于0。这说明长度越长，序列平衡性越好。当序列长度大于2000时，混沌序列的平衡度最小值仍大于0.4，但是物理随机序列的平衡度均已小于0.2，在长度为10000时接近于0。这说明经过处理后的物理随机序列的平衡性远远优于原始混沌序列。

3.3 物理随机序列相关性能分析

序列的自相关和互相关特性直接影响着扩频通信系统的好坏，具有优良相关性的扩频码能够减少系统的误码率和多用户干扰问题。自相关函数是描述随机信号x(t)在任意两个不同时刻取值之间的相关程度，而互相关函数是描述两列长度相同的随机信号x(t)，y(t)在任意两个不同时刻取值之间的相关程度。若x(t)是离散信号，则t仅在时间轴的离散点上取值，相关性公式［16］应如下表示：

利用公式（4）和（5）编写程序对长度均为8192的混沌序列和物理随机序列进行仿真，获得的自相关和互相关曲线分别如下图6和图7。图6（a）代表未经处理的混沌序列自相关曲线，自相关系数分布较为分散，绝对值最大值超过0.2。由图6（b）可以发现物理随机扩频序列在相关间隔为0时具有尖锐的峰值，其他间隔的值均在-0.05～0.05之间，类似于δ函数趋近于0的性质。对比可见，经过该系统后序列自相关系数明显下降，这表明自相关性能有所提高。

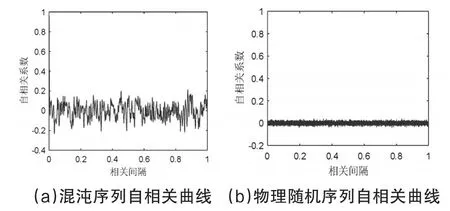
图6 混沌序列与物理随机序列自相关曲线

由图7（a）可见，未经处理的混沌序列的互相关系数绝对值超过0.05，互相关性较差。图7（a）中的真随机序列互相关系数值主要集中的-0.02～0.02之间，更加接近于0，说明真随机序列的互相关性优于原始混沌序列。扩频序列之间弱的相关性，才能使多个用户在同一频率的不同信道传输信息，即实现码分多址。

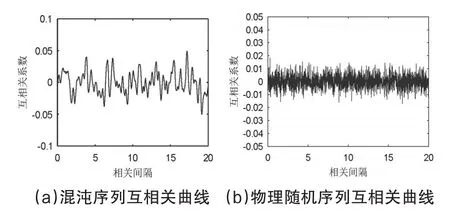
图7 混沌序列与物理随机序列互相关曲线

4 结论

针对扩频通信系统中，性能优良的扩频码直接影响系统的抗噪声与多用户干扰等性能因素，提出利用混沌信号作为物理熵源，通过后续处理数字化运算，获得数据率为4Gb/s的高速物理随机序列。经NIST软件套组对物理随机序列进行性能测试，结果表明保留4位最低有效位获得的真随机序列性能良好。最后对截短长度相同的物理随机码与混沌扩频码对比仿真，结果显示，物理随机序列获得的扩频码有着尖锐的自相关性，相关间隔大于0时，自相关系数也远小于混沌序列；其互相关性与混沌序列相比更加接近于0，表明正交性良好。这表明物理随机序列在相关性、正交性和均衡性上显著优于传统混沌序列，作为“好码”可显著提高扩频通信系统的抗干扰性能。

参考文献

［1］ Zhu Y，Zhang P，Deng M.Research on direct sequence spread spectrum communication system［J］.Ordnance Industry Automation，2013，32（2）：84-87.

［2］ 武立，柏逢明，罗奇，等.改进的调频差分混沌键控通信系统设计［J］.长春理工大学学报：自然科学版，2014，37（4）：129-132.

［3］ 李玉珍.基于混沌的扩频序列通信系统研究［D］.西安：西安电子科技大学，2015.

［4］ ShannonC E.Communicationtheoryofsecrecy systems［J］.Bell System Technical Journal，1949，28（4）：656-715.

［5］ 田日才.扩频通信［M］.北京：清华大学出版社，2007：1-25.

［6］ 侯娟.混沌伪随机序列的产生及其在扩频通信中的应用［D］.广州：华南理工大学，2012：21-41.

［7］ 柏逢明，沈柯.扩频序列超混沌保密通信系统设计研究［J］.长春理工大学学报：自然科学版，2003，26（3）：36-41.

［8］ 于银辉，王玥.混沌扩频序列的产生及其在CDMA中的应用［J］.吉林大学学报：信息科学版，2004，22（1）：23-26.

［9］ 俞斌，贾雅琼.一种新的混沌扩频序列及其性能分析［J］.电子技术应用，2013，39（1）：136-138.

［10］ 李增，冯玉玲，姚治海.半导体激光器输出混沌光的自相关性和带宽的研究［J］.激光与光电子学进展，2018，55（2）：021405-1-021405-6.

［11］ 杨海波，吴正茂，唐曦，等.反馈强度对外腔反馈半导体激光器混沌熵源生成的随机数序列性能的影响［J］.物理学报，2015，64（8）：084204-1-084204-8.

［12］ Zhang J Z，Wang Y C，Liu M，et al.A robust random number generator based on differential comparison of chaotic laser signals［J］.Opt Express，2012，20（7）：7496-7506.

［13］ Rukhin A，Soto J，Nechvatal J，et al.A Statistical test suite for random and pseudorandom number generators for cryptographic applications［J］.Applied Physics Letters，2015，22（7）：1645-1679.

［14］ Lang R，Kobayashi K.External optical feedback effects on semiconductorinjection laserproperties［J］.IEEE Journal of Quantum Electronics，1980，16（3）：347-355.

［15］ Chang-Geng L I，Zhou J L，Sun K H，et al.Balance analysis of four digital chaotic spread spectrum sequences［J］.Journal of Computer Applications，2008，28（1）：68-70.

［16］ 余振标，冯久超.一种混沌扩频序列的产生方法及其优选算法［J］.物理学报，2008，57（3）：1409-1415.