混沌激光调制实现二次谐波系统混沌反控制与混沌同步

王萌，冯秀琴，姚治海，王晓茜

（长春理工大学 理学院，长春 130022）

随着混沌动力学理论在保密通信、信息编码以及信息存储等方面应用研究的逐渐深入，混沌反控制与混沌同步的研究成为重要的研究方向。混沌反控制是在混沌信号有用时刻意产生混沌或者使混沌行为加剧，混沌反控制又被称为混沌生成或混沌合成。众多学者对不同系统的混沌反控制与同步进行了深入研究。陈关荣等利用状态反馈法，使闭环系统产生Devaney意义下的混沌［1］；Yang等研究了具有极限环的连续系统的混沌反控制问题［2］；汪小帆等利用时滞反馈法研究了最小相位系统的有关混沌的生成［3］；文献［4，5］指出利用耦合法和参量调制法等讨论研究了有关简并光学参量振荡器的混沌反控制与混沌系统的同步；文献［6］研究了玻色爱因斯坦凝聚系统的混沌反控制；文献［7］详细阐述了使A类和B类激光器通过附加自由度产生混沌激光的方法。

光学二次谐波系统是典型的一种非线性光学系统，分析研究光学二次谐波系统的混沌控制与同步对更深一步研究其他非线性光学系统的混沌控制与同步及其应用有着重要的指导意义。关于光学二次谐波系统的混沌动力学的研究已经有了很多具有重要意义的成果［8-11］，张喜和等通过使用方波脉冲以及锯齿波脉冲泵浦着重分析研究了光学二次谐波系统的混沌物理特性［12］；李建宇等利用延时反馈法也模拟实现了光学二次谐波系统的混沌控制与周期态同步［13，14］；常帅等研究了光学二次谐波系统的混沌耦合同步［15，16］；何军等利用方波脉冲实现了二次谐波系统的混沌控制［17］；文献［5］利用周期信号调制研究了光学二次谐波系统的混沌控制及其周期态同步，同时研究了光学二次谐波系统的混沌生成，至今未见更多关于二次谐波系统的混沌反控制与同步的研究成果报道。可见还可以对光学二次谐波系统的混沌反控制与同步进行更广泛深入的研究，本方案利用混沌激光调制研究光学二次谐波系统的混沌反控制与混沌同步。

1 混沌激光调制泵浦场反控制二次谐波系统的混沌

利用双环掺铒光纤激光器输出的混沌激光调制调制光学二次谐波系统的泵浦场，在腔损耗较低的条件下，调制后系统的动力学方程［17，18］：

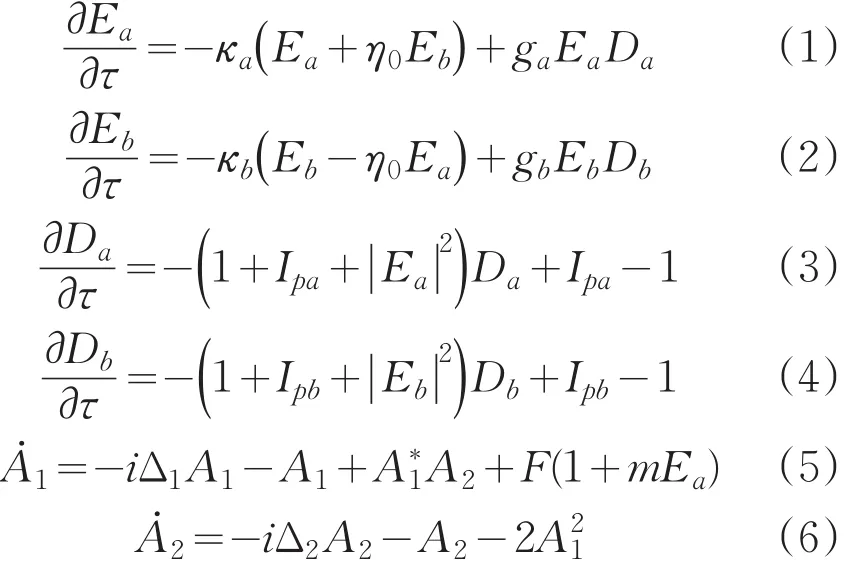
其中，（1）-（4）式为双环掺铒光纤激光器动力学方程，（5）-（6）式为光学二次谐波系统动力学方程，对应变量及其参数表1。

当二次谐波系统的泵浦为恒定值且F小于7.0时，系统参数为Δ1=Δ2=1.0时，二次谐波系统系统处于周期态，周期轨道和时间序列如图1，从中可见系统处于周期态。为使二次谐波系统从周期态转化为混沌输出，利用双环掺铒光纤激光器输出的混沌激光作为调制信号，使用混沌激光作为泵浦光。当双环掺铒光纤激光器参数为η0=0.2，ga=10500,gb=4700，κa=κb=1000，Ipa=Ipb=4 时，双环掺铒光纤激光器输出混沌激光［18］，用a环输出的混沌激光Ea调制二次谐波系统的泵浦场，当调制强度m＞0时，二次谐波系统转化为混沌输出，实现二次谐波系统的混沌反控制，当调制强度m=0.6时输出的混沌行为通过吸引子和时间序列图表征如图2所示，图2（a）和2（b）分别为基模和二次谐波模的混沌吸引子，图2（c）为基模输出的时间序列。

表1 （1）-（6）式参量及其含义对应表

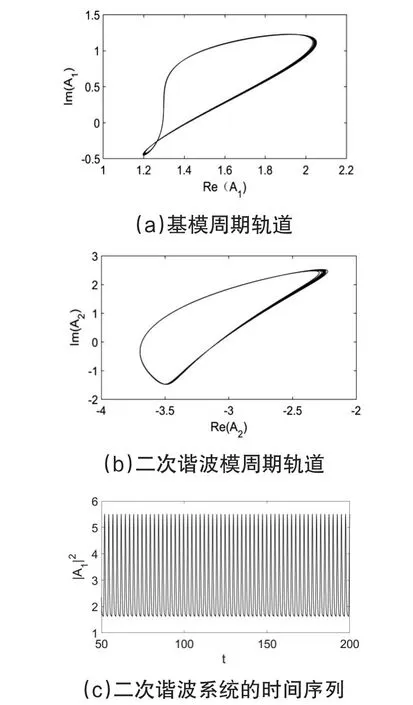
图1 稳恒泵浦二次谐波系统输出的周期轨道与时间序列F=6.0，Δ1=Δ2=1.0

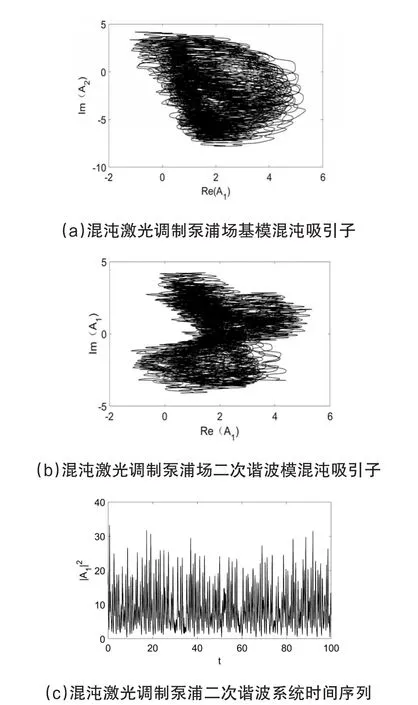
图2 混沌泵浦二次谐波系统输出的周期轨道与时间序列 F=6.0，Δ1=Δ2=1.0，m=0.6

利用（1）-（4）式输出的混沌激光同时调制两个二次谐波系统A和B的泵浦场，调制后同步系统A的动力学方程为（5）-（6）式表达，系统B的动力学方程为：

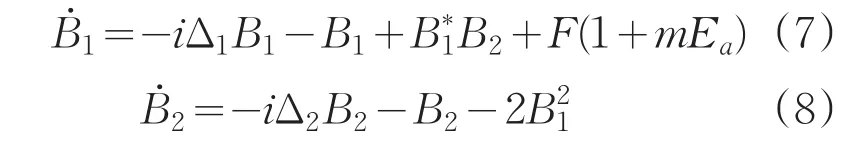
由于系统的初始条件不相同，而且混沌对系统的初始条件很敏感，A，B两个系统不会产生同步。数值分析结果表明，通过调整调制强度可以实现混沌同步，发现当调制增加到强度m=0.6时，系统B与C可以达到同步，随着调制强度的增加，当m＞0.6时，混沌输出同步速度加快。当初始条件为：A1=0.1+i0.1，A2=0.2+i0.2，B1=0.2+i0.2，B2=0.1+i0.1，耦合系数m=0.7时，系统的同步过程演化如图3所示。从图3（a）-（b）可见，系统B与C的基模和二次谐波模均达到完全同步，同步演化过程如图3（c）。

图3 混沌激光调制泵浦光学二次谐波系统混沌同步

2 混沌激光耦合调制实现二次谐波系统混沌同步

混沌激光耦合调制也可以实现二次谐波系统的混沌反控制与混沌同步，将双环掺铒光纤激光器输出的混沌激光通过耦合器耦合到光学二次谐波系统中，并对基模调谐参数进行调制，耦合调制后的动力学方程为：

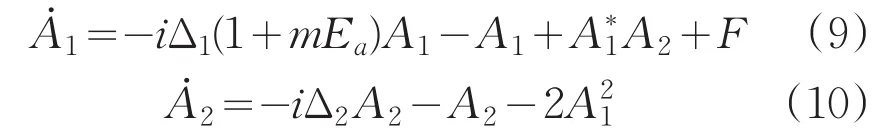
发现当调制强度m＞0.02时，二次谐波系统转化为混沌输出，通过耦合调制实现二次谐波系统的混沌反控制。当F=6.0，F=6.0，Δ1=Δ2=1.0，调制强度m=0.6时输出的混沌吸引子如图4所示，从中可见二次谐波系统处于混沌状态。

如果将双环掺铒光纤激光器输出的混沌激光同时耦合到两个二次谐波系统里并同时对基模调谐参数进行调制，调制后同步系统A的动力学方程为（9）-（10）式表达，系统B的动力学方程为：

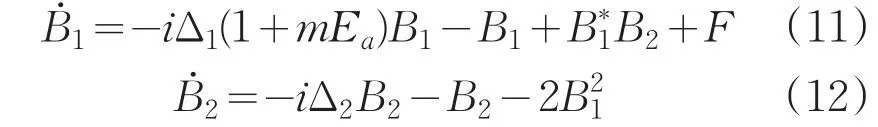
数值分析结果表明，通过调整耦合调制强度可以实现A和B系统的混沌同步，发现当调制增加到强度m=0.94时，系统A与B可以达到同步，随着调制强度的增加，当m＞0.94时，混沌输出同步速度加快。当初始条件为，A1=0.1+i0.1，A2=0.2+i0.2，B1=0.2+i0.2，B2=0.1+i0.1，耦合系数m=0.95时，系统的同步过程演化如图5所示。从图5（a）-（b）可见，系统B与C的基模和二次谐波模均达到完全同步，同步演化过程如图5（c）。

图4 混沌激光调制二次谐波系统基模调谐参数后的混沌吸引子

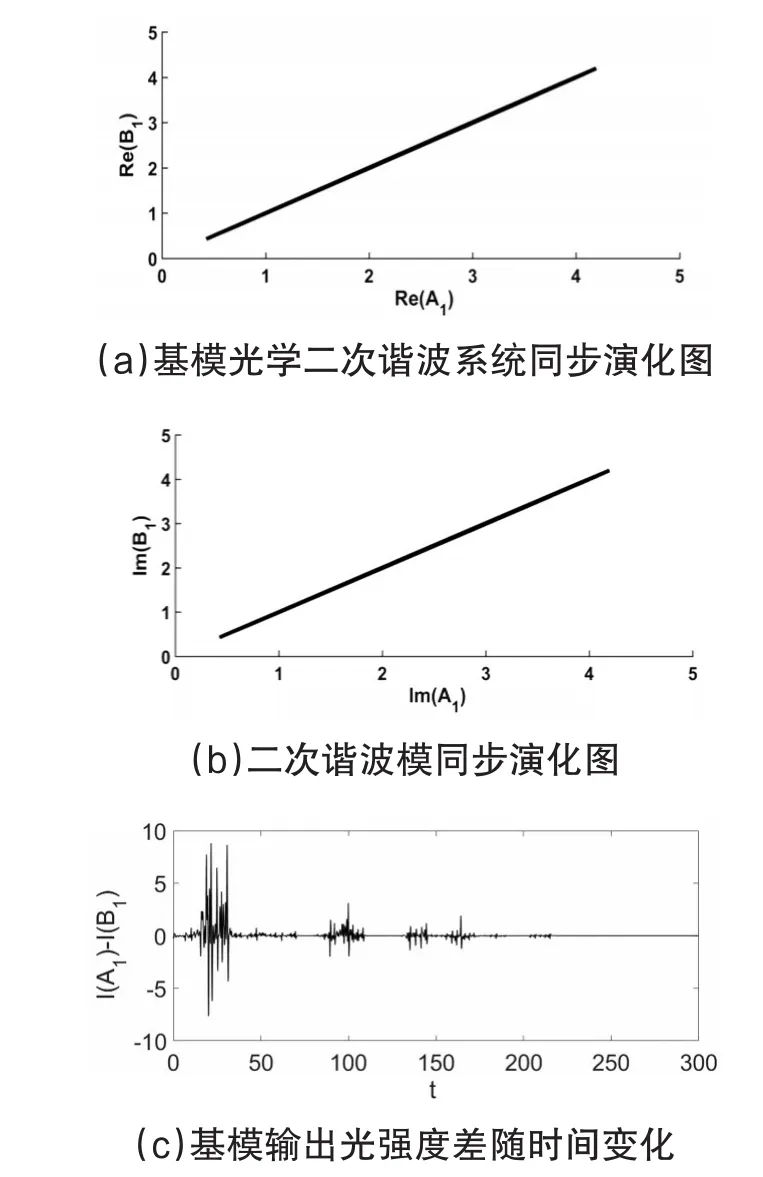
图5 混沌激光调制光学二次谐波系统调谐参数后的混沌同步

3 结论

利用混沌激光调制泵浦场，通过选择合适的调制强度，可以把光学二次谐波系统由周期态控制到混沌态，以实现光学二次谐波系统的混沌反控制。研究结果表明，两个或多个二次谐波系统的泵浦场同时被混沌激光信号调制，这些系统尽管初始条件不同，在确定的参数范围内，通过调整调制强度，可以实现两个或多个二次谐波系统混沌同步。不但可以利用混沌激光调制泵浦场实现光学二次谐波系统的混沌反控制与同步，调制二次谐波系统基模调谐参数也可以实现二次谐波系统混沌反控制与同步。以上得到的同步结果与周期信号调制和延时反馈调制不同，周期信号调制和延时反馈调制实现的是周期态同步，存在同步和反向同步两种同步方式。如果使用相同的混沌激光作为信号，以同样的方式同时对两个或多个二次谐波系统的泵浦场或基模调谐参数进行调制，再选取适当的调制强度，即可实现两个或多个二次谐波系统的混沌同步，这对实现多路信号同时进行混沌保密通信有着一定的参考价值。

参考文献

［1］ Chen G，Lai D.Feedback control of lyapunov exponents for discrete-time dynamical systems［J］.International Journal of Bifurcation& Chaos，1996，06（07）：1341-1349.

［2］ Ling Yang，Zengrong Liu，Guanrong Chen.Chaotifying a continuous-time system via impulsive input［J］.InternationalJournalofBifurcation & Chaos，2002，12（05）：1121-1128.

［3］ Wang X F，Chen G.Chaotification viaarbitrarily small feedback controls：theory，method，and applications［J］.International Journal of Bifurcation&Chaos，2000，10（03）：549-570.

［4］ 冯秀琴，姚治海，田作林，等.简并光学参量振荡器的混沌反控制与混沌同步［J］.光学学报，2010，30（3）：861-865.

［5］ 冯秀琴.光学参量振荡器的超混沌控制与同步研究［D］.长春：长春理工大学，2006.

［6］ 王志霞.玻色—爱因斯坦凝聚的混沌动力学研究［D］.长春：长春理工大学，2008.

［7］ 沈柯.光学中的混沌［M］.东北师范大学出版社，1999.

［8］ Grygiel K，Szlachetka P.Hyperchaos in second-harmonic generation of light［J］.Optics Communications，1998，49（7）：1043-1056.

［9］ Savage C M，Walls D F.Optical chaos in second-harmonic generation［J］.Optica Acta International Journal of Optics，1983，30（5）：557-561.

［10］ Aceves A，Holm D D，Kovačič G，et al.Homoclinic orbits and chaos in a second-harmonic generating optical cavity［J］.1997，233（3）：203-208.

［11］ Mandel P，Erneux T.Amplitude self-modulation of intracavity second-harmonic generation［J］.Journal of Modern Optics，1982，29（1）：7-21.

［12］ 张喜和，沈柯.调制脉冲泵浦相位共轭振荡器的动力学行为［J］.长春理工大学学报：自然科学版，1999，22（2）：1-6.

［13］ 姚治海，李建宇，冯秀琴，等.延时反馈调制泵浦场实现二次谐波的混沌控制与同步［J］.兵工学报，2011，32（6）：657-662.

［14］ Feng X Q，Jianyu L I，Yao Z H，et al.Chaotic control and synchronization in optical second-harmonic generation with parameter modulating by delay feedback［J］.Chaos An Interdisciplinary Journal of Nonlinear Science，2010，20（2）：023-120.

［15］ 常帅.光学二次谐波混沌控制与同步的研究［D］.长春：长春理工大学，2011.

［16］ 赵凤艳，冯秀琴，常帅，等.光学二次谐波系统混沌同步研究［J］.北华大学学报：自然科学版，2013，14（5）：530-533.

［17］ 何军，李元杰.光学二次谐波混沌的控制［J］.物理与工程，2000，10（6）：39-42.

［18］ 王荣，沈柯.延时线性反馈法控制双环掺铒光纤激光器混沌［J］.物理学报，2001，50（6）：1024-1027.