基于结构约束条件的相位恢复算法设计
2018-05-26赵一轩郭澄孙艳军
赵一轩,郭澄,孙艳军
(1.长春理工大学 光电工程学院,长春 130022;
2.哈尔滨工业大学 超精密光电仪器工程研究所,哈尔滨 150001)
相位恢复是利用易探测的强度信息重建波函数的过程。光的传播频率大约为1.6×1014Hz,目前并没有任何一种光学感应设备能够实现光波相位信息的直接测量,为此,需要引入一些间接测量方案对丢失的相位信息进行重构。目前,相位恢复技术可以分为以下两类:干涉测量法[1,2]和衍射测量法[3]。干涉测量法以参考光和照明光叠加的方式记录透射光波的信息,然后通过计算机处理的方式计算出目标物体的光场信息。虽然干涉法重构精度高,但是其重构容易被振动和热波动所影响,而且难以严格保证参考光和照明光的相干性。因此,干涉法对实验提出了极高的要求。
衍射法则通过样品的衍射图样直接进行目标重构,其具有结构简单、稳定性高等特点。根据计算方式不同,它可分为强度传输方程计算法[4]和迭代式相位恢复算法[5]两类。强度传输方程可在傍轴近似下利用亥姆霍兹方程求解而得,通过该方程可以直接求解目标的相位分布信息。该类方法无需迭代、无需相位解包裹,但是只能针对相位型物体或者透明样品。与之相反,迭代式相位恢复算法通过对目标光学系统建立迭代格式,利用迭代计算的方式进行目标重建。该类方法无需复杂的数学推导,且适用于各种类型的样品结构,因此近年来受到了广泛的关注。
迭代型相位恢复算法最早于1972年由Gerchberg等人研究电子显微镜的相位重构时所提出[6],该算法被称为GS算法(Gerchberg-Saxton algorithm)。该方法指出,如果像平面和远场衍射平面的强度可知,那像平面的相位可以通过衍射迭代计算的方式求出。随着该算法的提出,迭代型相位恢复算法现已被成功运用到X射线成像、自适应光学、相干衍射成像以及生物成像中[7]。虽然GS算法的提出具有开创性意义,但是它也存在着多种不容忽视的问题,例如其伴随的弱收敛性以及对初始值过于敏感。为了提高其收敛速度,Fienup基于反馈收敛的思想提出了混合输入输出算法(HIO)[8]。我国学者杨国桢和顾本源提出了YG算法,其将GS算法推广到了任意线性系统[9]。但是,这一系列GS算法的改进方案都依赖于样品的振幅信息已知,然而这一条件在无透镜衍射成像中却很难实现。为此,多参数测量、多方位测量的实施方案被用来缓解其对物平面的依赖,例如,利用精密针孔进行重叠扫描成像[10]、多距离衍射成像[11]、多波长衍射成像[12]等。
本文着眼于多距离衍射成像,为其定义了新的结构约束条件。通过该约束条件的限制,多距离衍射相位恢复的收敛速度和收敛精度都得到了极大的改善。
1 多距离相位恢复理论模型
迭代相位恢复问题实质上是求解一个病态方程组的问题,其最初的雏形是GS算法。GS算法最初被运用到电子显微镜中恢复焦平面的相位图像。其已知量为聚焦平面的强度图像g和其远场衍射斑I。它是典型的运用振幅-振幅信息恢复输入平面相位的算法。在GS算法中,傅里叶变换是其传递函数,因此算法中的输入平面和输出平面就分别代表着空域和频域。而GS算法的核心操作就在于分别为空域和频域中的计算值施加约束,其目的在于通过在迭代计算中不断施加固有的约束条件从而达到目标收敛的效果。相应的空域约束和频域约束就是分别利用在输入平面和输出平面实际测量得到振幅,替代每次迭代中所计算出的振幅、。GS算法计算步骤可以归纳为:(1)以随机相位初始化输入平面目标(平面);(2)对输入平面进行傅里叶变换从而得到目标的输出平面(测量平面)复振幅分布F;(3)频域约束,即以I替代 ||F,保持相位θ不变,从而组成新的输出平面复振幅F′;(4)对输出平面进行逆傅里叶变换从而得到输入平面的复振幅分布f′;(5)空域约束,即以g替代 ||f′,保持相位φ不变,从而组成新的输入平面复振幅f;(6)迭代重复步骤(2)-(5),直至得到满足需要的目标相位φ。
多距离相位恢复则是在目标后方衍射场测量多个距离下的强度图像,利用这多个测量图像的迭代计算从而恢复目标图像。多距离衍射成像是一类不借助任何目标光场的已知信息(Prior knowledge)而可恢复出其复振幅的相位恢复技术。
假设目标平面的复振幅函数分布为g,第n个衍射距离Zn下的测量图像为 ||In,那么目标复振幅函数g可通过以下迭代公式进行计算而得:

其中,k代表迭代次数,N为测量平面的个数,H和H-1为正向和逆向衍射传递函数。当k=1时,零初始化目标平面,即g1=0。而后,通过不断循环计算公式(1-3)就可以重构出目标平面的复振幅函数g。在菲涅耳衍射条件下,不同距离的衍射传递函数可表示为:
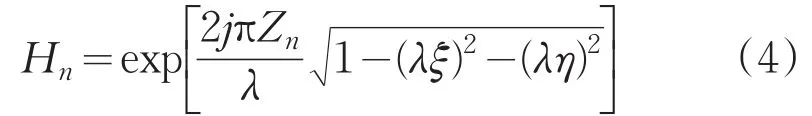
式中,(ξ,η)为频域坐标,λ为光学系统的通光波长。
2 基于结构约束条件的相位恢复算法设计
对于上述的多距离相位恢复算法,其存在的缺陷就是收敛速度缓慢。为此,本文利用设置约束条件的方式实现其加速收敛。Fienup在提出HIO算法的时候指出,如果在样品平面设置支撑约束条件,那么选择支撑条件的强弱就可以控制算法收敛的快慢。其对支撑条件的定义如下[8]:计算目标函数的边界,对边界内的局域进行相位恢复,然后对边界外的区域进行衰减或者直接置0。鉴于此,本文利用结构照明的方式定义支撑边界,然后将该结构支撑约束条件应用到多距离衍射成像中。
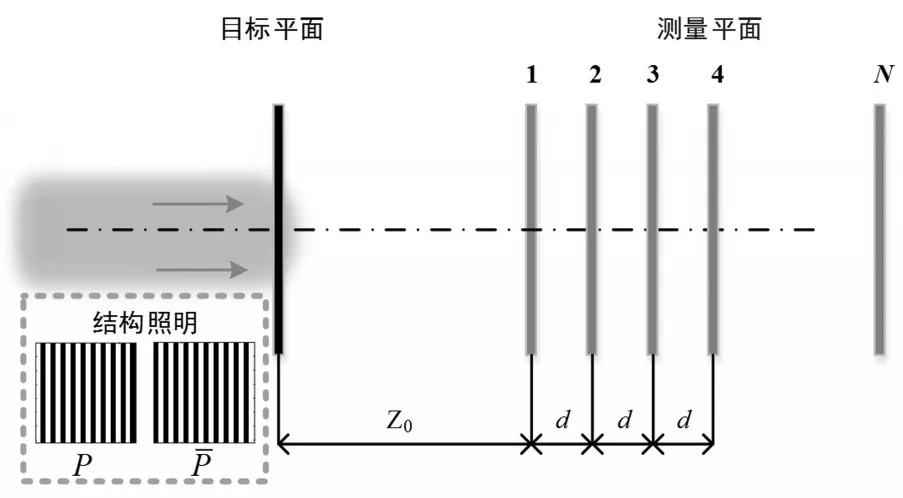
图1 基于结构约束条件的相位恢复算法结构图
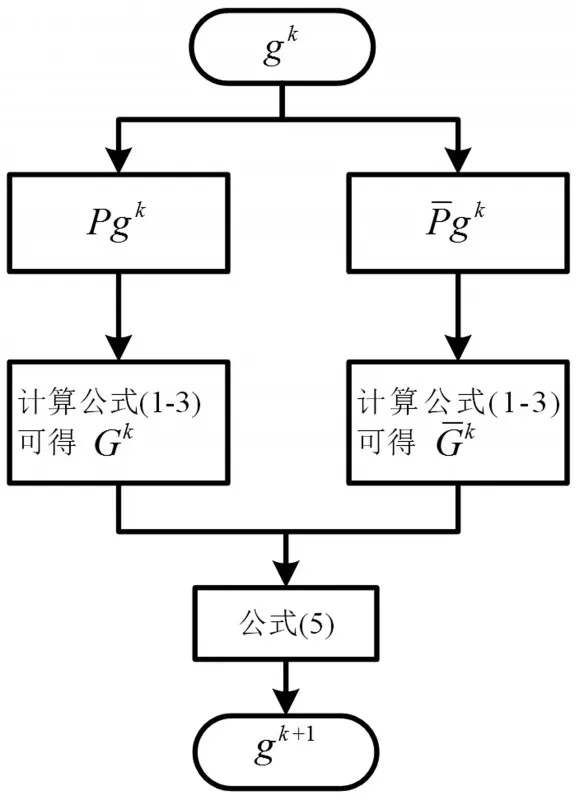
图2 基于结构约束条件的相位恢复算法流程图
图1为基于结构约束条件的相位恢复算法结构图,其在目标平面后方选择不同的衍射距离下设置测量平面,通过上节所述的迭代计算就可完成目标平面的图像重构。在等间距采集的前提下,设置多距离相位恢复的初始距离为Z0,间距为d,那么衍射距离就可表示为Zn=Z0+(n-1)d,n∈[1,N]。传统的多距离相位恢复要求使用平面波照明,本文在此基础上引入结构照明的思想,利用两个互补的结构光模式(P和Pˉ)对目标平面进行照明。图2为本文提出的改进算法的算法流程图。对于第k次迭代,互补的光照模式将分别产生两个物函数的出射波函数,即Pgk和Pˉgk。将这两个出射波函数带入迭代公式(1-3)可产生两个新的物函数估计Gk和Gˉk。毫无疑问,新产生的这两个物函数估计都只包含目标的局部信息。为此,第k+1次的目标函数估计可以通过下式合成而得:

公式(5)是改进算法的核心公式,其不但完成了图像的合成,也加强了相位恢复的约束支撑。而且,结构照明中其光斑模式是已知或可探测的,故公式(5)可实现相位恢复算法的紧支撑约束。
3 仿真分析
3.1 振幅型样品
利用自由空间相干衍射成像,将多距离相位恢复算法和其改进算法用于恢复纯振幅和纯相位型样品。结构照明作为约束支撑加速收敛的特性将在仿真分析中得到证明。其中,均方误差函数(Mean Square Error,MSE)被用来作为其图像恢复精度的评价函数,其定义如下:
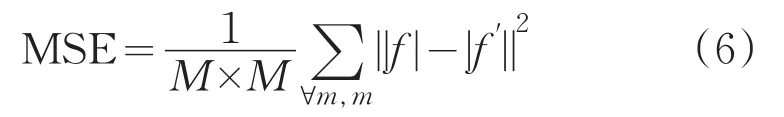
式中,M代表图像的尺寸,f′是真值图像,f是重构图像。MSE数值越小则图像恢复的精度越高。对于纯振幅型物体,本文选择分辨率板(图3(a))和灰度图像(图4(a))进行仿真分析。仿真参数如下所示:(1)图像尺寸为1mm × 1mm(360 × 360);(2)通光波长为532nm;(3)照明光束条纹周期为100μm;(4)测量次数N=4;(5)衍射平面初始距离Z0=20mm,间距d=2mm。为了保证对比分析的准确性,本节在多距离相位恢复仿真中的衍射距离分别为20、22、24、26mm。对于结构照明约束的多距离相位恢复,每个衍射距离对应两幅测量图像,因此其衍射距离只需选择为20mm和22mm。基于此,在测量次数相同的情况下,MSE越小代表收敛速度越快。设置迭代次数为120,分辨率板的仿真结果如图3所示。通过对比图3(b-d)可知,GS算法和传统多距离相位恢复算法的重构图像都出现了模糊和瑕疵,与之对应,施加照明约束的重构图像却清晰地重构出了分辨率板。而且就恢复精度而言,改进算法的MSE数值在三个算法中也是最小的。
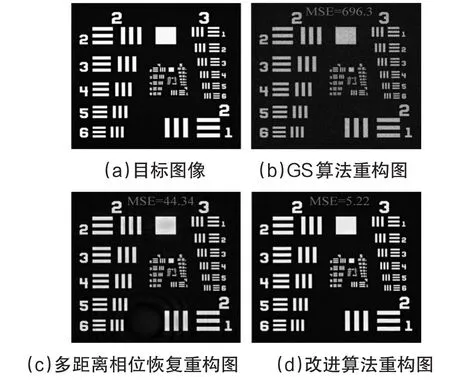
图3 二值型目标图像重构结果
灰度型纯振幅物体的重构结构如图4所示,它的仿真参数和图3一致。通过图4(b)和(c)的MSE对比可知,结构照明约束对于灰度图像依然有效。为了形象地描绘其收敛速度的增强,本文绘制了如图4(d)所示的振幅收敛曲线。其中,取对数后的均方误差(Logarithm of MSE,LMSE)被用来评价其收敛逼近程度。收敛曲线的对比进一步地证明了约束条件对相位恢复的加速效应。

图4 灰度型目标图像重构结果.
3.2 相位型样品
对纯相位物体进行仿真分析。振幅型物体对应纯振幅样品或者染色样品,而相位型物体则对应透明样品,相位型样品的透射函数只改变光场的相位分布,不会对光场进行强度的调制,最简单的相位型物体就是透镜。而且,在生命科学领域,活体测量因其无标记且不损坏生物样品内部属性而受到广泛关注。在对活体样品进行测量时,其聚焦平面的强度图像是透明的,无法通过强度信息对其进行检测,因此需要通过诸如相位恢复或者差分干涉相衬等技术对其相位信息进行重建。为了模拟纯相位样品,本节利用Matlab中的Peak函数作为样品的相位分布函数,利用一个全1矩阵作为其振幅分布函数。其中,图5(a-c)分别是目标图像的相位分布、传统多距离相位恢复算法的重构相位以及改进算法的重构相位。从图5(b)和(c)可以明显看出,如果不施加约束条件,传统的多距离相位恢复无法完整重构纯相位样品。相反,改进算法能完整重建出目标图像的相位分布。但是,图5(c)的重建相位仍然和目标相位有一定的差距。为此,不同测量次数下的相位收敛曲线绘制如图5(d)所示。
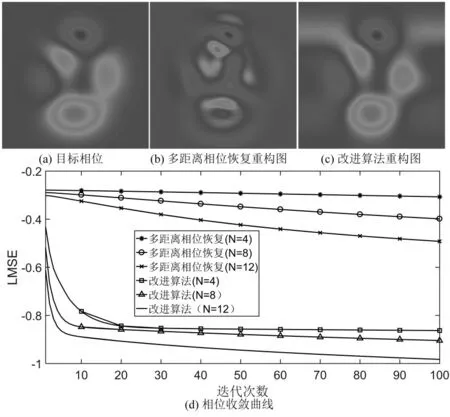
图5 相位型目标图像重构结果.
根据图5(d)的收敛曲线可知,测量次数的增加可提高重建相位的恢复精度,这便可以改善图5(c)中的瑕疵之处。而且,改进算法的收敛效果确实大大优于传统的多距离相位恢复。因此,结构照明约束的设置仍然可以加速相位型物体的重建速度。对于不同结构照明模式的准确实现,目前可以通过以下方案完成:利用空间光调制器[13]或者 Ronchi[14]光栅进行光束调制,形成明暗条纹,在偶数倍泰伯距离下放置样品,可实现文中P模式照明,在奇数倍泰伯距离下放置样品,可实现文中的Pˉ模式照明。
4 结论
本文将结构照明运用到多距离相位恢复中,通过不同的照明模式实现相位恢复的紧支撑约束,以此提高了多距离相位恢复的收敛速度和收敛精度。在相干衍射成像的数值仿真模型下,本文利用改进算法和传统的多距离相位恢复算法对纯振幅和纯相位型物体进行重构。通过重构结果可知,无论是纯振幅或者纯相位物体,结构照明约束都大大提高了收敛速度和收敛精度。此外,本文所提出的结构照明约束也可用于其他多参数相位恢复算法中。而且,对于纯相位物体,结构照明约束的使用解决了多距离相位恢复的弱收敛性以及收敛不稳定的问题,这对相位恢复在生物成像中的应用推广有重要的理论指导意义。
参考文献
[1] Bhaduri B,Edwards C,Popescu G,et al.Diffraction phase microscopy:principles and applications in materials and life sciences[J].Advances in Optics&Photonics,2013,6(1):212-217.
[2] Osten W,Faridian A,Gao P,et al.Recent advances in digital holography[J].Appl.Opt,2014,53(27):44-63.
[3] Shechtman Y,Eldar Y C,Cohen O,et al.Phase retrieval with application to optical imaging:a contemporary overview[J].IEEE Signal Processing Magazine,2014,32(3):87-109.
[4] 左超,陈钱,孙佳嵩,等.基于光强传输方程的非干涉相位恢复与定量相位显微成像:文献综述与最新进展[J].中国激光,2016,43(6):0609002-1-0609002-5.
[5] Guo C,Wei C,Tan J,et al.A review of iterative phase retrieval for measurement and encryption[J].Optics&Lasers in Engineering,2017(89):2-12.
[6] Gerchberg R W,Saxton W O.A practical algorithm for the determination of phase from image and diffraction plane pictures[J].Optik 1972,35(2):237-246.
[7] McleodE,OzcanA.Unconventionalmethodsof imaging:computational microscopy and compact implementations[J].Reportson Progressin Physics,2016,79(7):076001-076001-4.
[8] Fienup J R.Phase retrieval algorithms:a comparison[J].Appl.Opt.1982,21(15):2758-2769.
[9] 杨国桢,顾本源.光学系统中振幅和相位的恢复问题[J].物理学报,1981,37(5):410-413.
[10] Rodenburg J M,Faulkner H M L.A phase retrievalalgorithm for shifting illumination[J].Applied Physics Letters,2004,85(20):4795-4797.
[11] Liu Z,Guo C,Tan J,et al.Iterative phase-amplitude retrieval from multiple images in gyrator domains[J].J.Opt,2015,17(2):701-706.
[12] Bao P,Zhang F,Pedrini G,et al.Phase retrieval using multiple illumination wavelengths[J].Opt.Lett,2008,33(4):309-311.
[13] Gao P,Pedrini G,Zuo Chao,et al.Phase retrieval using spatially modulated illumination[J].Opt.Lett,2014,39(12):3615-3618.
[14] Feng S,Wang M,Wu J.Lensless in-line holographic microscope with Talbot grating illumination[J].Opt.Lett,2016,41(14):3157-3160.
