一种改进的快速FCM图像分割算法

徐路，蒋振刚

（长春理工大学 计算机科学技术学院，长春 130022）

由Bezdek J C等人提出的模糊C均值（Fuzzy C-means，简称FCM）算法［1］是通过优化目标函数对数据样本进行模糊聚类的方法，是一种可以应用于图像分割的较为重要的聚类方法［2-3］，为实现图像测量、配准［4-5］、融合以及三维重建的提供基础支撑。FCM算法对图像的模糊特征具有较强的鲁棒性，而且相对于硬聚类分割算法而言能保留更多的图像原始信息，具有更好、更稳定的聚类性能［6］，同时FCM算法是一种非监督模糊聚类方法，被广泛的应用于医学图像处理、图像分析等诸多范畴。

FCM算法应用于图像分割时可以减少人为的干预，且较适合灰度图像中存在较大不确定性的特点。虽然FCM算法用于图像分割有其特有优势，但也存在着明显不足［7］：算法聚类中心是随机初始化得到的，导致算法的迭代次数较多，没有考虑邻域点与中心点的相关性及目标函数对隶属度的约束［8-10］，导致算法的分割结果不够精确。

对随机初始化聚类中心的问题，很多学者进行了广泛深入的研究，并取得了一定的成果。文献［11］提出了一种结合灰度直方图的快速FCM算法，通过结合图像直方图的统计特性，基于直方图的峰值点来判别划分区间，从而初始化聚类中心，但未考虑峰值点小于聚类数目时的区间划分情况。王改华等人［12］提出一种改进算法，采取分块思想，利用均值特征对初始聚类的中心像素和中心数进行计算，然后根据块方差的比较结果计算不同的隶属度函数。但文章手动设定阈值较多，且先分块求均值，用欧式距离判别聚类中心，后分别计算均匀块与非均匀块的隶属度函数，在一定程度上提升了算法的计算复杂度。文献［13］提出了一种初始聚类中心的选取规则，即每个聚类中心之间的距离应该保持设定的最小阈值，通过不断的调整阈值的大小，使选取聚类中心可在多个可行域上进行，从而避免局部收敛的缺点。但如何选取到合适的阈值还需进一步的研究。张翡等人［14］通过将图像从像素空间映射到其灰度直方图空间，然后平均划分区间，同时考虑密度与距离的乘积来确定初始聚类中心，但其区间划分方法对灰度值较为集中的图像效果不理想。文献［15］提出了在精简数据集，压缩迭代数据量的基础上，运用灰度值对应频数与距离的联系初始化聚类中心的算法，由于依旧采用平分区间的思想，在区间划分上仍存在准确性问题。Zhou D等人［16］提出一种新算法，首先分段输出前景区域和后景区域，然后在分段结果基础上引用核函数求得聚类中心，利用具有偏置场的模糊聚类算法划分空间邻近像素，然而该算法消耗了过多的时间将像素仔细划分到其更相似的簇中，并且一些参数设置的影响，在研究中没有详细揭示，如γ。

考虑到上述问题，本文重点从准确划分区间求取聚类中心点，同时兼顾算法计算复杂度的关键点出发，针对FCM算法随机初始化聚类中心的问题进行改进，提出一种基于确定初始聚类中心的快速FCM图像分割算法。该算法通过最大类间方差法［17］划分图像灰度区间初始化聚类中心，从而减少算法的迭代次数。该算法不仅可以应用于FCM算法中，同时可应用于多种采用随机初始化聚类中心的FCM类算法（如FCM_S、FCM_S1及FCM_S2等算法）中，提升算法计算速度。

1 FCM分割算法

FCM算法是一种应用于图像分割的重要聚类方法，其基本思想是通过迭代寻找到最优的聚类中心vi以及隶属度uik，以使目标函数Jm（U，C）取得最小值，从而实现图像的优化分割。

并且满足下列约束条件：

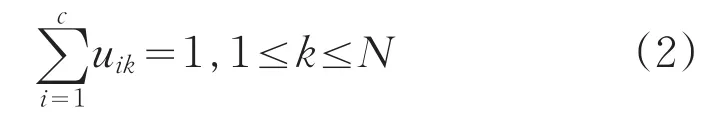
数据集X=(x1,x2,x3,…,xN)∈Rs为图像灰度值的集合，s是样本xk（k=1，2，3，…，N）的维数，c代表聚类的类别数，N代表待聚类样本数据集中包含的数据点的个数，uik表示X中第k个样本数据点归属于第i类的隶属度，vi（i=1，2，3，…，c）为每个聚类的聚类中心，2≤c≤N，m∈［1，+∞）为聚类加权指数，控制着数据划分过程的模糊程度，若m=1，模糊C均值聚类便退化成硬C均值聚类，很多研究表明，m=2的取值较为理想，d2ik（xk，vi）为第k个样本数据点到第i类聚类中心vi的欧式距离，U={uik}代表一个n*c维的矩阵。

在约束条件下，根据拉格朗日乘子法可以得到使得目标函数式（1）取极小值的必要条件：

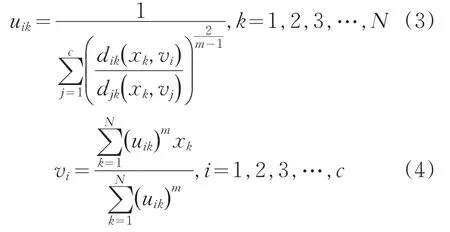
隶属度函数和聚类中心由式（3）、式（4）不断迭代更新，直到目标函数J取得最小值时，FCM算法收敛，并取得最终的聚类中心vi。

FCM算法收敛也可以通过检测聚类中心vi和模糊隶属度uik的变化来完成。当连续两次求出的聚类中心vi或模糊隶属度uik的差值小于一定的阈值时，则认为算法收敛，并取得最终的聚类中心。

最后使用最大隶属度函数法来对分类结果进行去模糊操作，完成图像分割。用Ck表示第k个待分类样本点xk隶属于第i类的程度，有

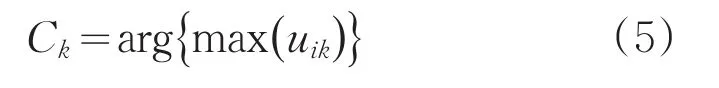
2 确定初始聚类中心的快速FCM算法

本文采用最大类间方差法在图片整个灰度范围内找到最优的阈值点，然后用该点把灰度区间分成两个子区间。再依次通过最大类间方差法继续划分子区间，根据限定条件选取划分阈值，直到达到设定的划分阈值个数，进行FCM算法分割。

2.1 确定聚类中心步骤：

（1）计算待分割图像的直方图，保存每一个像素的灰度值出现的概率。确定聚类数目C。

（2）采取最大类间方差法取得阈值t1，将区间划分为［0，...，t1］和［t1+1，...，L-1］（若只将图像分为两类取t1做划分阈值T1，划分区间。）。

（3）在区间［0，...，t1］和［t1+1，...，L-1］上，根据最大类间方差法的原则，分别取得阈值t2，t3，比较t1，t2，t3附近的方差值（数据归一化后求得的方差值）Di（i=1，2，3），取较大的Di值所对应的ti值作为划分阈值T1，T2。

（4）设上述取得t1，t2做划分阈值T1，T2，则依次在［0，...，T2］，［T2+1，...，T1］中分别用最大类间方差法得到阈值t4和t5，及其附近的方差值Di（i=4，5），并与在步骤（1）中余下的区间内求得的阈值t3对应的D3比较，选择最大Di（i=3，4，5）值对应的阈值作为划分阈值T3。

（5）对T3新划分得到的两个子区间按如上所述求阈值t及其附近区域的方差值D，并与前面剩下的区间算得的阈值对应的D值进行如上比较，依次取得划分阈值T，直到达到设定的数目为止。

为了准确的划分区间，在如下情况时，优先操作下述方法：

情况1：若比较用最大类间方差法求得的阈值对应的方差值时，方差差值 ΔDi（i=1，2，3）小于ξ（ξ值可根据图像类型自定）时，取使得新划分子区间距离值同时取得最大（和最大，差最小，和最大优先，和相同时取差最小）的阈值t做划分阈值T。

情况2：与已确定的相邻的边界过近（不存在波峰点），判定此阈值无效，不取此阈值，在下次比较时，计算其划分的有波峰点的子区间内的阈值，若此阈值有效，以其做比较，否则舍弃，若比较阈值均为无效阈值，则按情况1方法处理。

（6）因为靠近聚类中心的像素点对本类别的隶属度应大于远离聚类中心的像素点对本类别的隶属度，所以设定区间段中像素点，对第k个类别的隶属度uik赋值为1，对其他类别的隶属度赋值为0。因此，得到聚类中心的初始化公式：

设tl为区间起点，th为区间终点，h(i)为像素i所出现的概率，L值为256。

2.2 图像分割步骤

（1）设置聚类个数C，权重指数m，终止阈值ε，最大迭代次数Lmax，按2.1中确定聚类中心的方法算出聚类中心vi。

（2）按照公式（3）计算模糊隶属度uik。

（3）重复公式（3）到（4），直到＜ε或者达到最大迭代次数Lmax。（b为算法迭代次数。）

（4）根据隶属度最大原则，依照公式（5）做去模糊化处理，完成图像分割。

3 实验结果

为了验证本文所提出算法的有效性，分别采用FCM算法及本文算法在MATLAB R2016a编程环境下对20幅模拟脑图像，20幅脑MR图像，10幅心脏CT图像，10幅细胞图像，10幅人脸图像，10幅自然图像进行图像分割及结果比较（图像均由512×628个像素组成）。实验平台为Windows 7，Intel（R） Xeon（R） CPU E3-1200V23.10GHz，RAM 10GB，实验设置参数m=2，目标函数收敛的阈值ε=0.00001，迭代最大次数Lmax为200，FCM算法的迭代次数及CPU时耗取5次均值，方差差值ξ=0.0001，判断t值附近方差D时取t值附近50像素的区间范围。

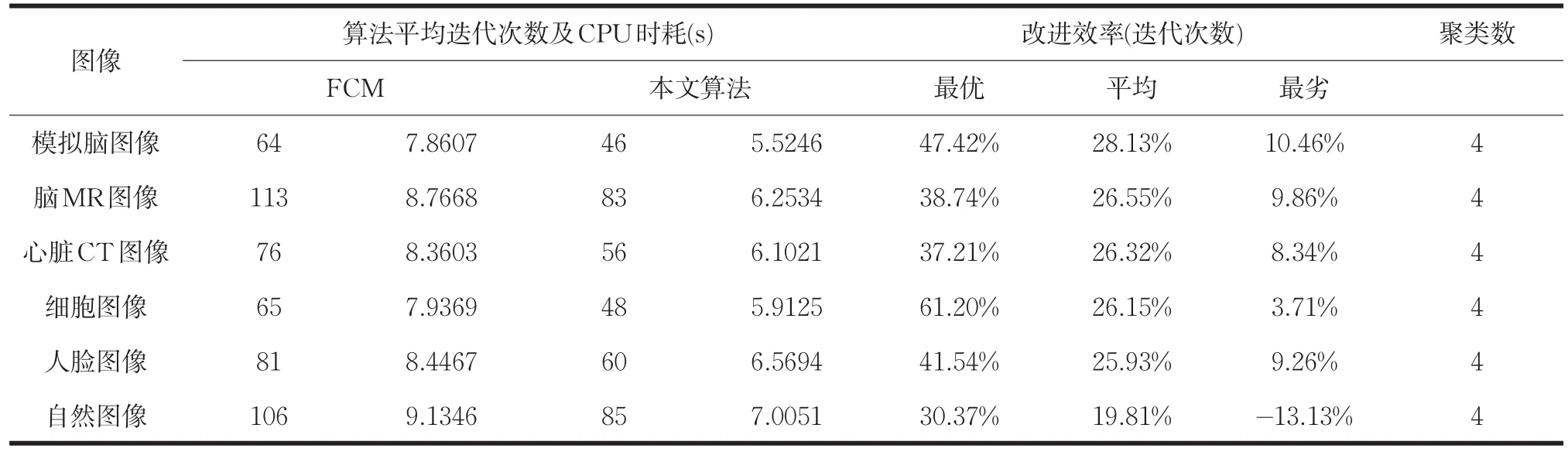
表1 FCM算法与本文提出的算法对多组图像进行分割的数据统计

实验结果表明（表1）：使用本文提出的算法对上述多组图像进行图像分割，所需的迭代次数与对应的CPU时耗较之随机初始化聚类中心的FCM算法在多数案例中均有所降低，其中，实验最优情况为降低算法迭代次数61.20%，最劣情况为增加算法迭代次数13.13%。

由表1中数据可以看出本文提出的算法较之FCM算法对模拟脑图像与脑MR图像的平均改进效率更为明显，对自然图像的平均改进效率较为低下。因为脑图像相似灰度值分布区域较为集中，计算聚类中心时，更为精确。而由于自然图像的多样性，部分自然图像较之其他图像灰度分布具有不确定性，使得其直方图灰度值抖动较大，计算聚类中心点时精确性有所欠缺。

图 1（a）为一幅模拟脑图像，（b）为其对应的FCM算法及本文提出的算法的分割结果（因为本文提出的算法只针对确定算法的聚类中心做出改进，所以分割结果与FCM算法分割结果相同），（c）为其对应的直方图。聚类数目设置为C=4（将图像分为脑白质、灰质、脑髓液和背景）。

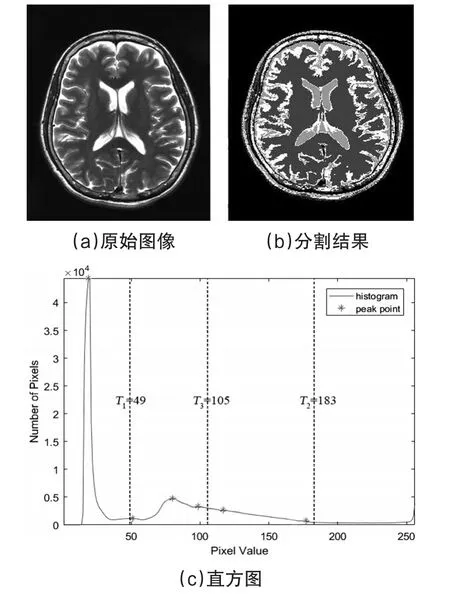
图1 模拟脑图像的原始图像、分割结果及直方图

按照2.1小节的算法步骤可以得出图1（c）中的划分阈值分别为49，105，183，在划分的区间中应用公式（6）求出聚类中心vi（i=1，…，4）值分别为19.3075，80.5983，134.6177，234.2696，与最终系统算得的聚类中心值 17.5988，80.0802，135.2761，238.8832较为接近，从而较之随机初始化聚类中心的FCM算法的减少了算法的迭代次数，加快了算法的收敛速度。

图2（a）为一幅自然图像，（b）为其对应的FCM算法及本文提出的算法的分割结果，（c）为其对应的直方图。聚类数目设置为C=4（将图像分为前景、中景、远景和天空）。

图2 自然图像的原始图像、分割结果及直方图

按照2.1小节算法步骤（1）至（3）可以得出图2（c）中的划分阈值分别为T1=58，T2=202，在步骤（4）中比较阈值31，123，236附近的灰度值方差时，由于阈值236附近灰度值抖动较大，以致在选取划分阈值时，选取了不理想的划分阈值T3=236，在划分的区间中应用公式（6）求出聚类中心vi（i=1，…，4）值 分 别 为 30.1598，115.2752，224.4136，250.6030，最终系统算得的聚类中心值25.9405，62.4323，160.3823，239.0716，相差较大，故算法的收敛速度较之随机初始化聚类中心的FCM算法并无优势，甚至增加算法迭代次数。

表2为采用FCM算法与本文提出的算法对图1（a）、图2（a）进行图像分割的迭代次数与运行时间的数据统计，从表中可看出，对于图1（a），本文所提出的算法所需的迭代次数少于随机初始化聚类中心的FCM算法的迭代次数，CPU时耗也较之FCM算法有所减少。而对于图2（a），本文提出的算法迭代次数及CPU时耗均多于随机初始化聚类中心的FCM算法。

表2 FCM算法与本文提出的算法对图1、图2分割的迭代次数与运行时间

4 结论

本文提出一种结合最大类间方差法的快速FCM图像分割算法。算法充分利用图像统计直方图信息初始化聚类中心，以减少FCM算法的迭代次数，提高图像分割效率。实验表明本文提出的算法对于相似灰度值分布区域较为集中的图像（如医学图像）效果较为明显，可以快速得到系统最终确定的聚类中心，进而加快算法的收敛速度，而算法对直方图灰度值抖动较大的图像效果不够理想。该算法可应用于采取随机初始化聚类中心的FCM相关的算法中，通过确定初始聚类中心，可以有效提高FCM类算法的运算效率。

参考文献

［1］ Bezdek J C，Ehrlich R，Full W.FCM：The fuzzy c-means clustering algorithm［J］.Computers&Geosciences，1984，10（2）：191-203.

［2］ ZhangD，WangY.Medicalimagesegmentation based on FCM clustering and rough set［J］.Chinese JournalofScientific Instrument，2006，27（12）：1683-1687.

［3］ Chen W，Giger M L，Bick U.A fuzzy c-means（FCM）-based approach for computerized segmentation of breast lesions in dynamic contrast-enhanced MR images［J］.Academic Radiology，2006，13（1）：63-72.

［4］ 何巍，魏国栋，师为礼，等.基于点云的膝关节胫骨三维CT与MRI图像配准［J］.长春理工大学学报：自然科学版，2015，38（5）：131-135.

［5］ 陈克寒，杨华民.利用光线投射法虚拟X光线图片进行基于灰度的2D/3D配准算法研究［J］.长春理工大学学报：自然科学版，2016，39（2）：103-106.

［6］ YangJ.Fuzzyc-means'performancecomparison with hard clustering and improvement［J］.Computer Knowledge&Technology，2008，4（S2）：192-194.

［7］ 张军贤.基于改进模糊聚类算法的医学图像分割研究［D］.武汉：华中科技大学，2012.

［8］ Feng Y，Dong F，Xia X，et al.An adaptive fuzzy C-meansmethod utilizing neighboring information for breast tumor segmentation in ultrasound images［J］.Medical Physics，2017，44（7）：3752-3760.

［9］ Venu N，AnuradhaB.Multil-Kernelsintegration for FCM Algorithm for medical image segmentation using histogram analasis［J］.Indian Journal of Science&Technology，2015，8（34）：1-8.

［10］ Guo F，Wang X，Shen J.Adaptive fuzzy c-means algorithm based on local noise detecting for image segmentation［J］.Iet Image Processing，2016，10（4）：272-279.

［11］ 张小峰.基于模糊聚类算法的医学图像分割技术研究［D］.济南：山东大学，2014.

［12］ 王改华，李德华.A fast and effective fuzzy clustering algorithm for color image segmentation［J］.北京理工大学学报：英文版，2012，21（4）：518-525.

［13］ 张慧哲，王坚.基于初始聚类中心选取的改进FCM聚类算法［J］.计算机科学，2009，36（6）：206-209.

［14］ 张翡，范虹，郝艳荣.结合非局部均值的快速FCM算法分割MR图像研究［J］.计算机科学，2014，41（5）：304-307.

［15］ 郭荣传，叶水生，闵泉，等.改进的快速FCM图像分割算法［J］.计算机系统应用，2009，18（7）：33-36.

［16］ Zhou D，Zhou H.A modified strategy of fuzzy clustering algorithm for image segmentation［J］.Soft Computing，2015，19（11）：3261-3272.

［17］ Gonzalez R C，Wood R E，Eddins S L.Digital image processing using MATLAB.Second Edition［M］.北京：电子工业出版社，2013.