一种基于最小量化误差流水线ADC校准算法

牛胜普，唐 鹤，李泽宇，陈科全，彭析竹，张 波

（电子科技大学，成都 610054）

1 引言

随着现代CMOS工艺的发展，器件特征尺寸逐步降低，芯片功耗面积逐步下降，低功耗高速高精度ADC实现成为可能。但工艺进步带来的并非全是优点，对于模拟电路来说，工艺进步带来的缺点同样明显。CMOS器件特征尺寸降低，模拟电路电源电压进一步下降，受此影响作为模拟电路中关键电路的运算放大器，其重要指标诸如高增益、宽带宽、宽线性输入范围也越来越难以同时实现[1]。通信系统中常用的高速高精度ADC如流水线ADC中所用关键运放也越来越难以实现。高速高精度流水线ADC中运算放大器通常无法同时满足信号建立速度和建立精度的要求，往往牺牲信号建立精度以保证建立速度，从而使得流水线ADC关键模块乘法数模转换器（MDAC）产生增益误差。MDAC增益误差如果不加以校准将会严重影响流水线ADC诸如ENOB、SNDR、SFDR等关键指标[2]。

高速高精度流水线ADC校准算法研究由来已久，目前校准算法大致可以分为前台校准算法和后台校准算法。前台校准算法例如LMS校准算法[3]，校准时需要打断ADC的正常工作，但其校准精度较高，一般对ADC模拟部分改动较小，ADC模拟部分设计复杂度较低。后台校准算法如PN码伪随机噪声注入校准算法[4]，校准时不需要打断ADC正常工作，可实时跟踪校准，但其往往需要ADC模拟设计做出相应调整，增加了模拟电路设计的复杂度。本文所提出的基于最小量化误差流水线ADC校准算法属于前台校准算法。

本论文基于最小量化误差原理，通过逐级搜索流水线ADC每级增益，进而对流水线ADC输出数据进行还原，对还原后的信号进行快速傅里叶变换分析，当有效位数等指标满足要求时即可认为增益校准正确，从而实现流水线ADC校准。通过本文校准算法校准后的ADC ENOB可达13.20 bit，SNDR可达81.23 dB，SFDR可达87.99 dB，积分非线性（INL）最大为1 LSB，微分非线性（DNL）在正负0.1 LSB之间。与未校准的ADC相比，ADC各项性能指标提升显著。

2 校准算法设计背景

流水线ADC中结构如图1所示，输入信号经采样保持电路采样后送入流水线单元ADC，各单元ADC在双相不交叠时钟的控制下交替进行采样和余差放大。在单元ADC内部，采样相时信号同时经乘法数模转换器MDAC和子ADC采样，子ADC通过比较产生数字码Di；保持相时Di经MDAC与输入信号相减产生余差，MDAC对余差进行放大，余差经放大后送入下一级，作为下一级的输入信号。图2[5]为传统流水线ADC中MDAC的结构示意图，MDAC输入输出关系如公式(1)、(2)所示：

图1 传统流水线ADC中结构示意图

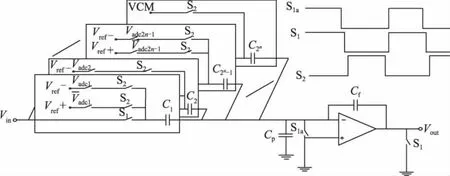
图2 传统流水线ADC中MDAC结构示意图[5]

3 最小量化误差校准算法原理与实现

3.1 最小量化误差校准算法原理

如图3所示，对于N位流水线ADC，信号经过采样保持电路流入第一级Stage1，采样相时信号同时被子ADC和MDAC采样，信号经子ADC比较产生数字输出Di；保持相时，数字码Di经MDAC中DAC还原并与输入信号做差，然后放大产生余差电压Vres。在此过程中，子ADC对输入信号量化会产生量化误差εq。其输入输出关系如式（3）、（4）所示：

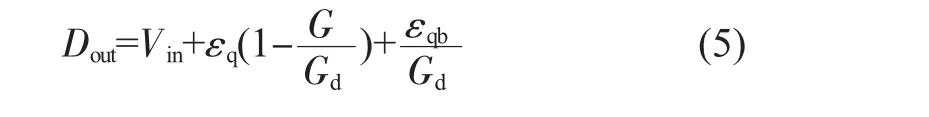
图3 流水线ADC第N级量化模型

图4 流水线ADC系统量化模型

由公式(6)可知，当经过校准后，校准出流水线ADC每级增益Gdi与实际增益Gi越接近，Dout与Vin之间误差越小，即量化误差越小，校准精度越高。

从公式(6)可以发现第一级的量化误差εq1比第二级量化误差εq2对Dout影响大，第二级量化误差εq2比第三级量化误差εq3对Dout影响大，后面几级依此类推。因此，我们一般从校准第一级增益Gain1开始从前往后逐级校准每级增益。

3.2 最小量化误差校准算法实现

本文基于MATLAB程序校准流水线ADC每级增益。

公式(7)将第二至最后一级所有Dout等效为第一级模拟输出Vout1，其中最后一级Flash ADC数字输出Dout(Flash)利用公式(8)还原成其模拟输入Vin(Fiash),其中m指Flash ADC位数。利用Vout1和数字输出Dout1进行还原得到Vin1，对还原后的Vin1进行快速傅里叶变换FFT分析，计算有效位数ENOB。对Gain1每个取值计算得到的ENOB进行保存，最终对所有第一级增益取值对应的ENOB进行分析，ENOB最大值所对应的增益值即为第一级增益Gain1，认为此时第一级增益即为第一级实际增益。

对于固定步长的取值，步长越小则需要校准的次数越多，校准越精确，但需要时间越长，本论文校准精度取万分之一；对于每一级增益从理想值左右两侧以固定步长取值的次数，在不低于一万次时一般不会出错，出错的容忍范围较大。

对于第二级增益Gain2的校准类似。校准第二级增益时需把除第一级外的其他级增益设置为理想增益值，第二级增益Gain2从理想值左右两侧以固定步长取值，第二级增益Gain2每取一个值则利用校准公式(7)将第三至最后一级所有Dout等效为第二级模拟输出Vout2，利用Vout2和数字输出Vout2进行还原得到Vout1，然后继续利用校准公式(7)对Vout1进行还原得到Vin1，对Vout1进行还原得到Vin1时用到的Gain1是利用第一步已经校准得到的Gain1。对还原后的Vin1进行FFT分析，计算ENOB。对于Gain2每个取值计算得到的ENOB进行保存。最终对所有第二级增益值对应的ENOB进行分析，ENOB最大值所对应的增益值即为第二级增益Gain2，认为此时第二级增益即为第二级实际增益。

对于第三级、第四级以及第N-1级增益的校准方法与第二级增益校准方法类似。

当把流水线ADC前N-1级增益校准后，还原得到流水线ADC的输入信号Vin，对还原后的Vin进行FFT分析，计算得到ENOB、THD、SFDR，即可得知流水线ADC的系统性能。

利用最小量化误差增益校准算法校准流水线ADC每级增益，对于流水线ADC每级增益范围要求低，每级低增益依然可以实现较高校准的精度。此外，本算法具有高效快速准确的特点，能够实现流水线快速精确校准，从而提高流水线ADC的系统性能。

4 仿真结果

本论文所设计流水线ADC最小量化误差校准算法可校准流水线ADC采样速度从低速（kHz）到高速（GHz），有效位数从8 bit到15 bit。以基于SMIC55LL工艺流片实现的如图5所示的14 bit 250 Msps流水线ADC校准为例，如图6、图7所示，在输入信号频率110 MHz、采样信号频率250 MHz的情况下，校准后流水线ADC DNL比校准前明显下降。

图5 14 bit 250 Msps流水线ADC结构

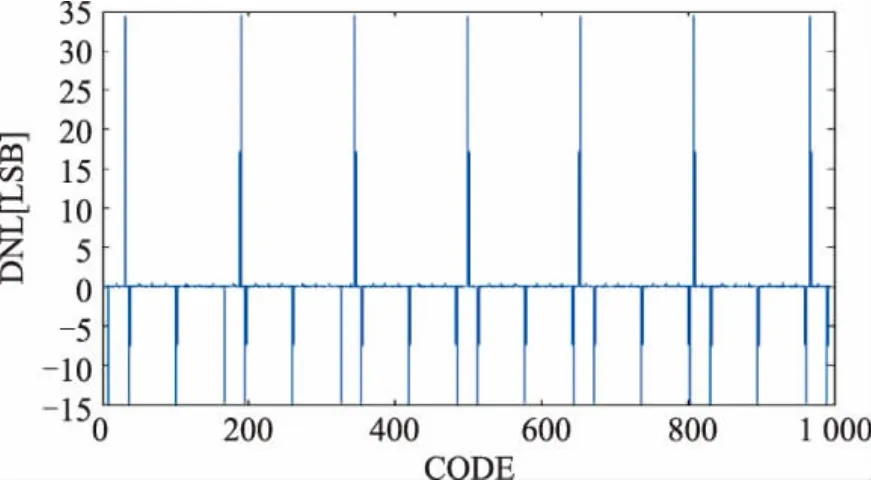
图6 14 bit 250 Msps流水线ADC校准前DNL

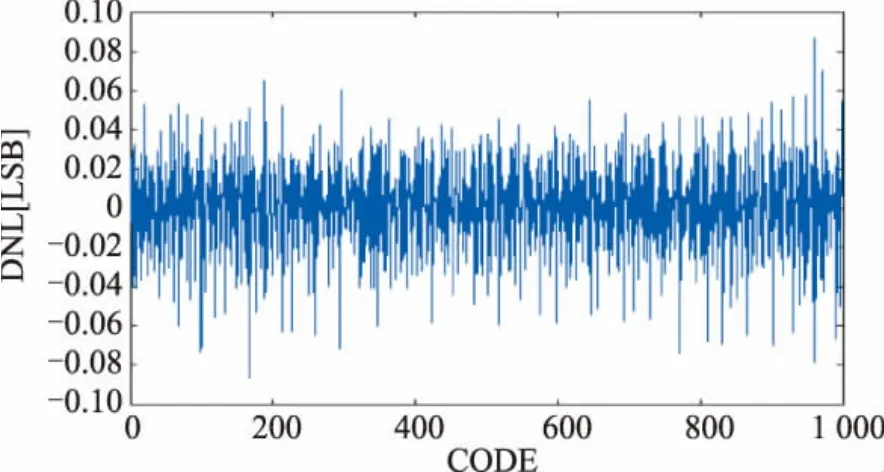
图7 14 bit 250 Msps流水线ADC校准后DNL

图8 、图9为校准前后流水线ADC的INL。校准后流水线ADC INL相比校准前由超过20个LSB下降到不到1个LSB。

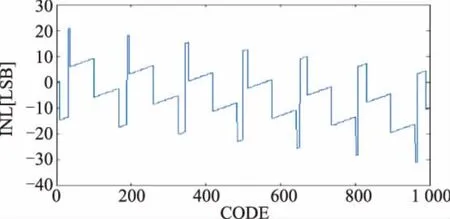
图8 14 bit 250 Msps流水线ADC校准前INL

图9 14 bit 250 Msps流水线ADC校准后INL

图10 和图11以及表1为校准前后的动态参数变化。校准后流水线ADC SNDR相比校准前由35.35 dB提升至81.23 dB，SFDR由44.07 dB提升至87.99 dB，THD由45.37 dB提升至85.79 dB。由以上分析可知，基于最小量化误差校准流水线ADC，可明显提高流水线ADC的静态性能和动态性能。

图10 14 bit 250 Msps流水线ADC校准前动态参数

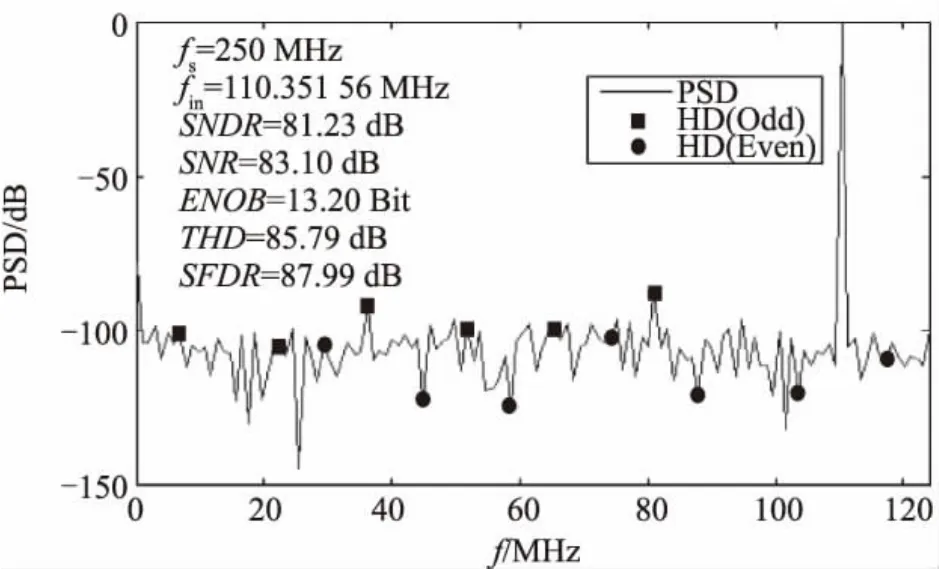
图11 14 bit 250 Msps流水线ADC校准后动态参数

表1 14 bit 250 Msps流水线ADC校准前后动态参数变化

5 结论

本论文提出了一种基于最小量化误差流水线ADC校准的算法，通过逐级搜索流水线ADC每级增益使得流水线ADC总量化误差达到最小，从而使得流水线ADC有效位数（ENOB）最大，完成校准。本文提出的校准算法应用于一款14 bit 250 Msps的流水线ADC，经校准后ADC ENOB可达13.20 bit，信噪失真比SNDR可达81.23 dB，无杂散动态范围SFDR可达87.99 dB，同时ADC静态特性、动态性能均得到明显改善。

参考文献：

[1]Sansen W M C.Analog Design Essentials[M].Springer US,2006∶181-220.

[2]F Maloberti.Data converters[M].Springer Netherlands,2007∶47-76.

[3]Yun R,Qin Y,Signell S.LMS-based calibration of pipelined ADCsincluding linearand nonlinearerrors[C].European Conference on Circuit Theory and Design.IEEE,2007∶348-351.

[4]梁上泉.流水线模数转换器伪随机序列注入后台快速数字校准技术研究[D].合肥：合肥工业大学,2011∶50-64.

[5]Ahmed I.Pipelined ADC Design and Enhancement Techniques[M].Springer Netherlands,2010∶20-23.

[6]彭蓓.结合数字校正技术的纳米CMOS流水线ADC设计[D].北京：北京工业大学,2011∶20-21.

[7]Behzad Razavi.Design of Analog CMOS Integrated Circuits[M].西安：西安交通大学出版社,2002∶138-161.

[8]B D Sahoo,B A Razavi.10-b 1-GHz 33-mW CMOS ADC[J].IEEE Journal of Solid-State Circuits,2013,48(6)∶1442-1452.