弹簧振子受迫振动的数值模拟

孔 健

（合肥幼儿师范高等专科学校 学前教育系，安徽 合肥230011）

关于振动的学习一直是高校物理课程重要内容.在教学中主要讨论的是最简单的振动——简谐运动，求解振动的运动方程，并帮助学生了解振动的规律.但是在实际生活中遇到的振动，大多数都是非常复杂的，要考虑的因素很多，其运动方程也不像简谐运动那样容易的求解出来.受迫振动就属于这类复杂运动.在受迫振动中，由于振动体不断的受到外界力的作用，本身的振动性质将被改变，甚至产生共振，并且不同的因素会对受迫振动产生不同的影响.

随着计算机的普及运用，对于一些复杂物理问题的数值模拟变得越来越简单.通过计算机语言和一些绘图软件，可以很轻松的绘制出物体运动的轨迹以及各个物理量的变换曲线，更加直观的展现出物体的运动规律.通过模拟和绘图，可以跳过解析求解复杂的运动方程，帮助学生更加直观方便的去理解一些物理问题.

受迫振动的牛顿运动方程实际上是二阶常微分方程.在已知初始条件的情况下，数值计算就是解微分方程的初值问题，有很多方法都可以对其进行求解［1］.在此，为了帮助学生更加全面了解受迫振动的运动演变过程，以竖直放置的弹簧振子为例，采用数值计算的方法，从牛顿第二定律出发，不做任何近似，直接对运动方程进行数值求解和模拟，从而对受迫振动的运动过程进行全面的展示和研究.

1 运动方程的数值求解

假设竖直悬挂的劲度系数为k的轻弹簧下面连着一个质量为m的小球，构成弹簧振子，小球除受到重力、弹力和空气阻力以外，还受到一个频率为ω的简谐振动的外界驱动力f.在大学物理的计算中，当运动物体的速度不太大的情况下，所受的空气阻力经常简化为F=-βv，式中β为常数［2］.因此，在模拟中，假设空气阻力与小球运动的速率成正比，比例系数是β.小球静止时，弹簧的伸长量为l，以此时小球的位置作为坐标原点，竖直向下建立坐标系.忽略弹簧的质量，根据牛顿第二运动定律，小球的运动方程可以写为：

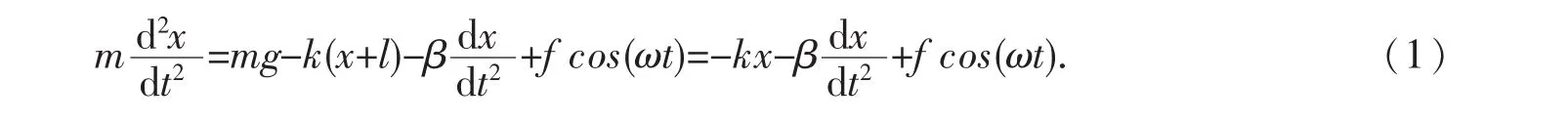
利用降阶法［3-4］，令：

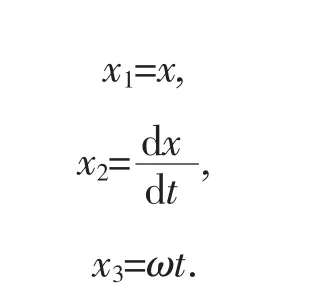
将上述二阶常微分方程变成一阶常微分方程组.

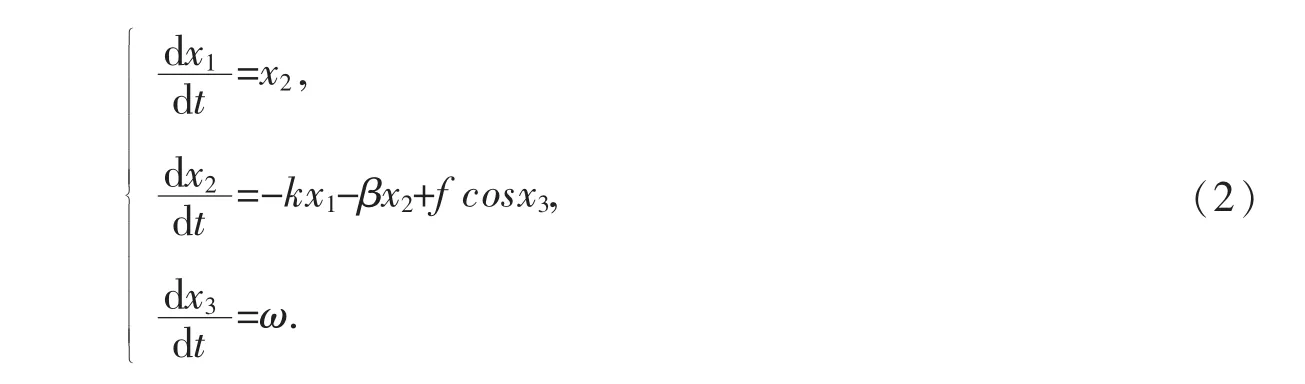
在数值计算方法中，四阶Runge-Kutta［1-2］是一种公认较为精确的方法，它可以用来求解一阶的常微分方程以及一阶常微分方程组.在此采用四阶Runge-Kutta方法，利用计算机语言Fortran 95进行编程［5］，数值求解方程组（2），从而得到位移x以及速度dx/dt，数值计算与解析结果见图1.

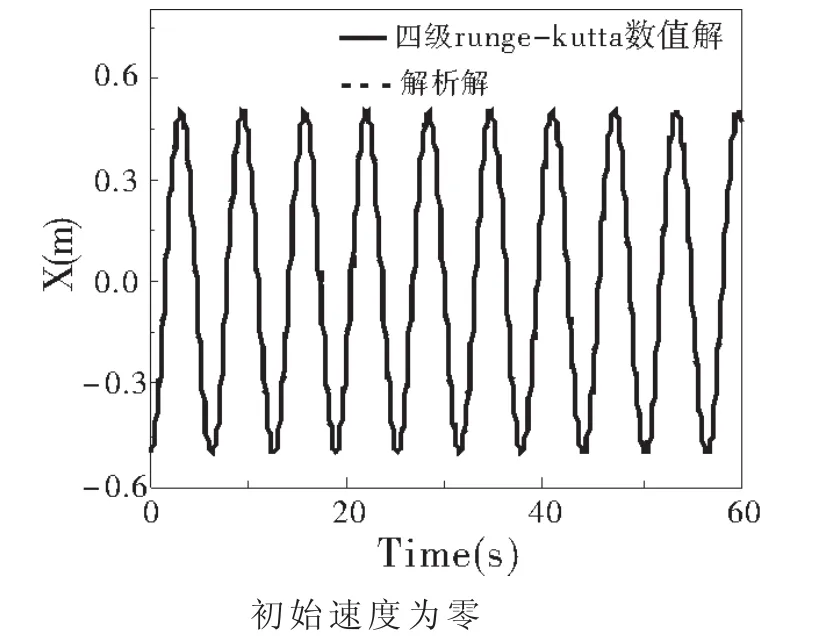
图1 四阶Runge-Kutta数值计算 (实线)与解析结果(虚线)

2 计算结果的模拟与讨论

首先计算了在无阻力，无驱动力的情况下小球的运动.假设t=0时，小球离开平衡位置一定的初始位移，初始的速度为零.为简单起见，令m=1 kg,k=1.由图1可见，此时小球的运动为周期性的简谐运动.此时将方程（1）可以简化成：

方程（3）可以非常简单的精确求解的，其通解为：

带入初始条件计算出振幅A和初相φ，得到的结果与数值模拟的结果是一致的，这也说明的数值模拟方法是正确且合适的.此外由公式（4）可知，小球作简谐运动的固有频率：这与大学物理教学中的分析是一致的［2］.

然后加入阻力的作用，如图2(a)所示，在不同的阻力作用下，小球振动的位移随时间会逐渐减小，最后静止下来.阻力的作用是对小球原有简谐运动的耗散.阻力系数越大，小球的运动损耗得越快，会更加迅速的达到静止.分别以小球的位移和速度作为横坐标和纵坐标，得到小球运动过程中的相图（图2(b)）.可见，不论弹簧振子的初始状态如何，在阻力的作用下，小球运动的相轨迹最终都会归为原点，也就是静止在平衡位置.

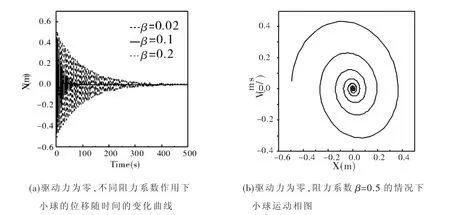
图2 小球的位移曲线和运动相图（驱动力为零，β=0.5）

加入周期性驱动力的作用.此时，小球的运动实质上是阻尼振动与外驱动力振动两个运动的合成.在阻力和驱动力的双重作用下，小球原本在固有频率下的简谐运动会被打乱，变得复杂.在图3(a)中，设置外界驱动力 f=±0.8 N，阻力系数β=0.5.在外界驱动力与阻力的大小相差不多的情况下，经过一段很短时间的调整，驱动力不断对小球做功，给振动体传递能量，最后振动的步调趋于稳定.同样的现象在图3（b）的相图中显示得更加明显.不论小球初始的位移和速度是多少，最后小球振动的相轨迹都将归于一个椭圆，即为极限环.这说明小球最终的受迫振动是能量不变、频率不变的稳定运动.

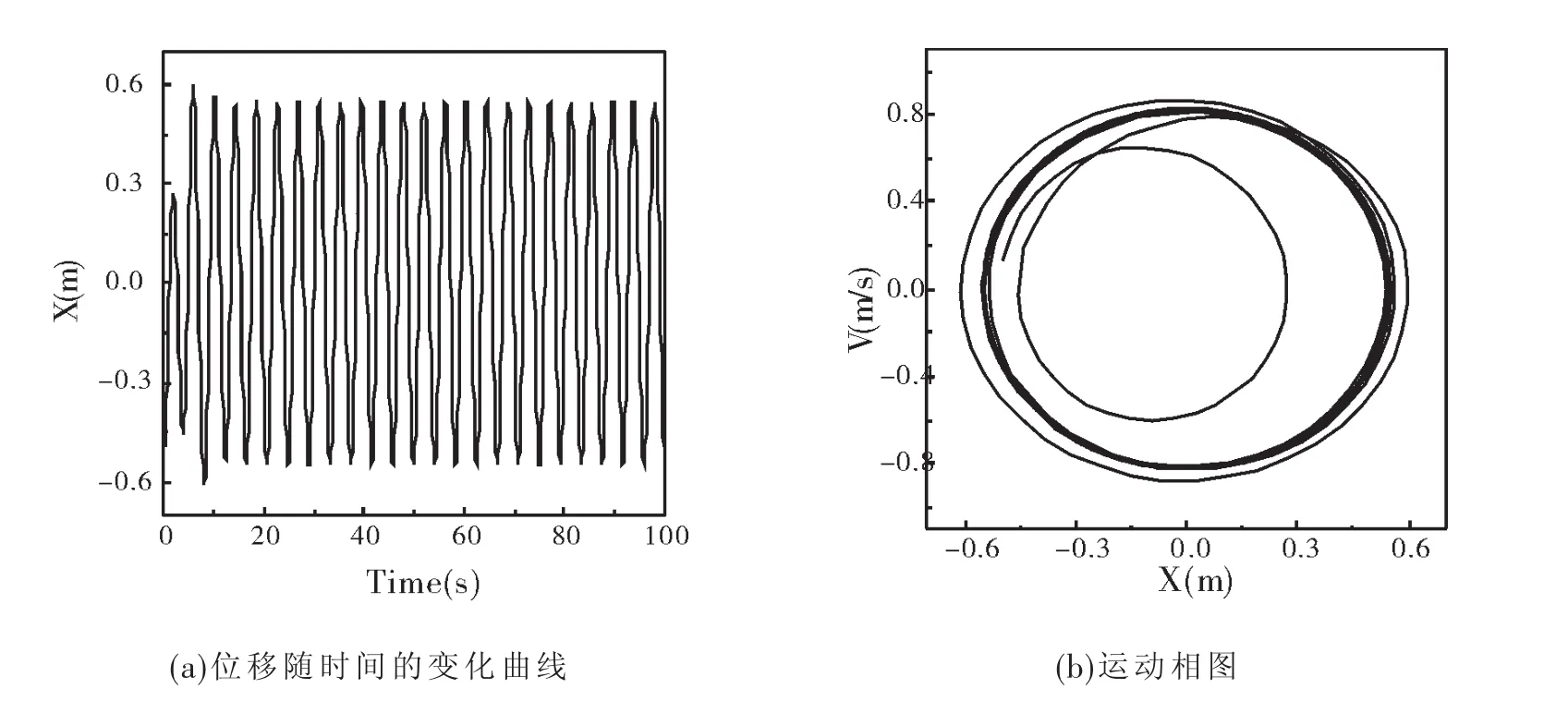
图3 小球的位移曲线和运动相图（驱动力f=±0.8 N，β=0.5）

在驱动力不变的情况下，逐步减小阻力系数，观察受迫振动的变化.为了更加清晰的讨论小球的运动位移随时间的变化，分不同的时间段进行了展示.图4(a)中是前200 s内小球的运动曲线.可见随着阻力的减小，弹簧振子固有频率下的简谐运动与驱动力的相互协调的过程将变长.在β=0.02的情况下，即使到了200 s，系统仍未达到稳定振动.在这个运动体系里，小球固有频率和驱动力的频率在振动的过程中是相互竞争的关系.而阻力的作用实际上是使得小球原本在固有频率下的简谐运动不断的耗散殆尽最后消失，随后转变成由驱动力控制下的振动.因而，阻力越小，耗散的过程越慢，最后达到稳定的时间就越长.在图4(b)中，随着时间的延长，在450～500 s的时候，三种阻力系数下的受迫振动都达到了稳定.比较发现，阻力的减小可以延长受迫振动自我调整的时间，但是对最后的稳定振动的影响并不大.随着阻力系数从0.5减小到0.02，小球达到稳定时，振动的振幅稍稍增强.在小球达到由驱动力控制的稳定振动后，阻力小，能量损失就大，因而振幅会增大.但这种通过阻力系数的调节并不显著.

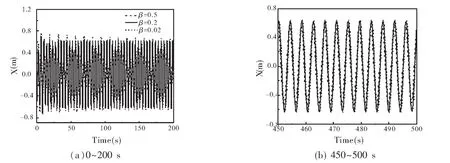
图4 小球位移随时间变化曲线（驱动力f=±0.8 N，阻力系数取不同的值）

与阻力的影响不同的是，在外界驱动力和阻力都不变的情况下，最后的稳定振动的振幅是与驱动力的频率有很大关系.由公式（5）可知，在所研究的系统中，小球的固有频率为1.当驱动力的频率与小球的固有频率相差很大时，小球最终的稳定振动的振幅并不大.改变驱动力的频率，当外界驱动力的频率越靠近小球振动的固有频率时，趋于稳定振动的振幅就会越大.图5展示了阻力系数不变，在不同频率的驱动力的影响下，弹簧振子的受迫运动.可见，随着驱动力的频率逐渐靠近弹簧振子的固有频率，稳定运动的振幅会迅速增大.在极限情况下，当驱动力的频率与固有频率相等时，振幅达到最大，即为日常所说的共振现象.可见频率是影响最终振幅的关键因素.当然如果保持驱动力的频率不变，而增大驱动力f=±2.0 N，同样也可以使得最后稳定振动的振幅增大（图6），但是调节的效果没有频率显著，振幅也不会像发生共振的时候增大得的那么明显.

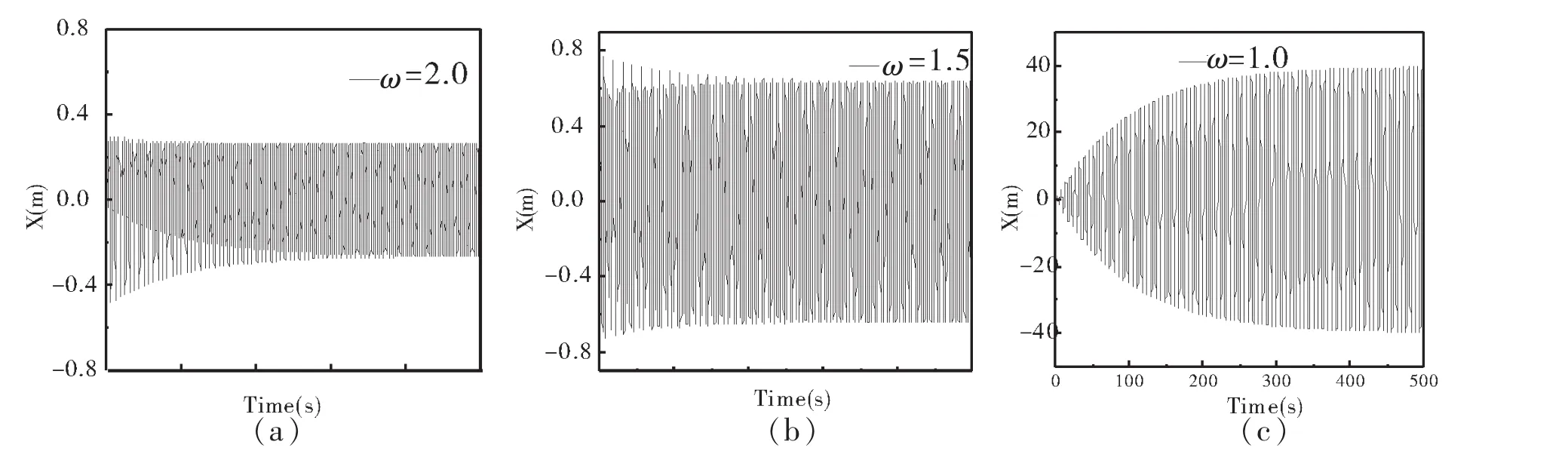
图5 驱动力频率取不同值情况下，弹簧振子的运动曲线（驱动力f=±0.8 N，β=0.02）

最后改变了弹簧振子的劲度系数，使其增加大到10.此时弹簧振子的固有参数变成了保持f=0.8 N,β=0.02，ω=1.5不变，模拟出的小球的位移随时间的变化如图7所示.弹簧振子劲度系数变大增强了固有频率下的简谐振动，使之更有能力与驱动力以及阻力抗衡.因而整个受迫振动在达到稳定状态之前，相互协调的过程就会被延长，变得更加明显.

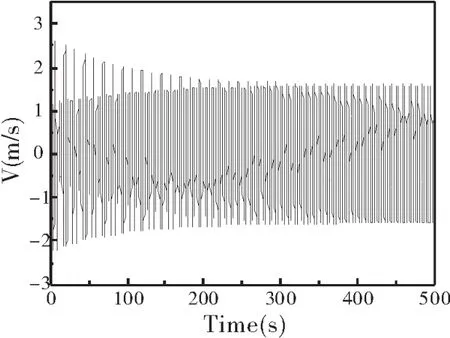
图6 弹簧振子的运动位移随时间的变化曲线（f=±2.0 N，β=0.02，ω=1.5）

3 总结

研究发现通过数值求解运动方程的方式，利用绘图软件可以清晰的展示以弹簧振子为研究对象的受迫振动中振子的位移随时间的变化曲线以及相轨迹.计算结果表明受迫振动是一种很复杂的运动，涉及到弹簧振子在固有频率、驱动力以及阻力三者之间的相互协调.但不论参数如何变化，弹簧振子最后的运动都会趋于一个较为稳定的周期性振动.周期性驱动力的频率是影响最后稳定振动振幅的关键性因素.当驱动力的频率与弹簧振子的固有频率相等时，受迫振动的振幅将被大幅度增加，即发生了共振现象.此外阻力系数的减小和驱动力振幅的增大都会在一定程度上增大受迫振动的振幅，并且会非常明显的延长受迫振动趋于稳定的过程.最后，弹簧劲度系数的提高会增强弹簧振子原本固有频率下的振动的能量，因而在趋于稳定运动之前会经历更加复杂及漫长的自我调整的过程.

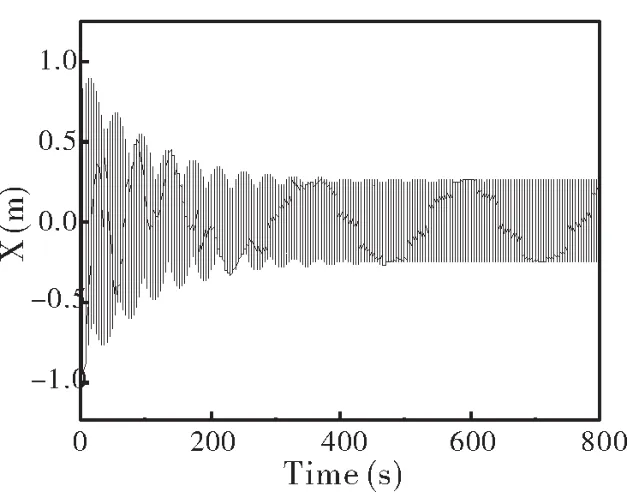
图7 弹簧振子的运动位移随时间的变化曲线（f=±2.0 N，β=0.02，ω=1.5，k=1）

［1］Burden R L,Douglas F J.数值分析［M］.7 版.冯烟利，朱海燕，译.北京：高等教育出版社，2005:241-248.

［2］韩家骅，汪洪.大学物理学［M］.3 版.安徽：安徽大学出版社，2015:34-35,146-150.

［3］彭芳麟.计算物理基础［M］.北京：高等教育出版社，2010：178-185.

［4］刘金远，段萍，鄂鹏.计算物理学［M］.北京：科学出版社，2015:96-125.

［4］龚天富.程序设计语言与编译——语言的设计和实现［M］.2版.北京：电子工业出版社，2003:33-95.