定子线棒改造施工风险评价研究

张 弛

（湖南五凌电力工程有限公司，湖南 长沙410004）

0 引言

近年来，我国各地水电站出现众多因电腐蚀而产生的定子线棒损坏情况，因此对定子线棒进行改造施工也就势在必行，但定子线棒改造过程中工艺复杂、定子及定子线棒本身易损伤，稍有不慎则易造成损坏，继而造成经济损失和工期延误，如未及时发现更可能对机组造成极其恶劣的影响。由此可见，对定子线棒改造技术进行施工风险评价研究，对发现事故、准确认识安全形势具有十分重要的意义。本文拟用集对分析与三角模糊数耦合模型对定子线棒改造施工进行风险评价。

1 集对分析基本理论

集对分析[1-2]是以集对及其联系度的概念，描述系统中存在的确定与不确定性及转化规律的一种系统分析技术，它先对不确定系统中2个有关联的集合A和B构造集对（如物质与能源、信息与智能等）H （ A, B ），用μA～B表示其联系度。

式中：n为集合A和B的表征特性数；s为集合A和B所共同具有的表征特性数；p为集合A和B中相对立的表征特性数；f为集合A和B既不共同具有、又不对立的表征特性数；s + f + p = n ；a、b和c为非负实数，且a、b和c需满足归一化条件a+b+c=1；a=s/n，为同一度，表示集对的同一程度；b=f/n，为差异度，表示集对差异的不确定程度；c=p/n，为对立度，表示集对的对立程度；i为差异不确定系数，在[-1,1]内取值，有时i也仅起标记作用；j为对立度系数，j=-1。c与a对ABμ～联系度的作用正好相反。

当μ在[-1,1]变化时，反映了A和B 两个集合的同一和对立度。当联系度μA～B=-1时，说明A和B 两个集合完全同一，可以满足目标要求；当联系度μA～B=1，说明A和B 两个集合完全对立，不能满足目标要求。

2 三角模糊数

三角模糊数用来评价数据资料较少或具有较大模糊性的工程具有一定优越性，不仅可以实现表征信息的模糊性，还可以实现对数据处理的随机性[3-4]。集对分析方法虽然能够表征定子线棒改造施工风险评价的确定性特征，但是在运用集对分析理论描述不确定性时存在较大的难度，这是因为对联系数的差异度系数没有确切的表达式，鉴于上述问题，本文提出采用三角模糊数来描述差异度系数的模糊特性，定义G为实数R（ R ∈ [ 0,1]）上的一个模糊数，定义一个隶属函数()G xμ，若隶属函数()G xμ可以表示为：

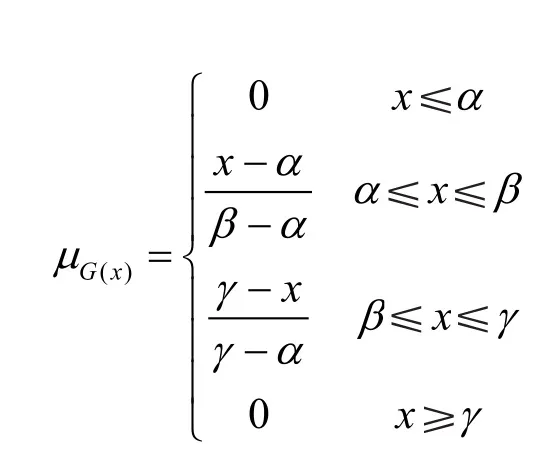
则称G为三角模糊数，记为 A = ( α, β, γ)，其中α≤≤β≤≤γ。

三角模糊数的隶属函数值域在[0,1]之间，而集对分析中差异度系数i的取值范围为[-1,1]，为了使两者在值域范围上具有一致性，将三角模糊数的隶属函数值域从[0,1]拓展到[-1,1]，这为建立基于集对分析与三角模糊数定子线棒改造施工风险评价的综合评价模型提供了理论基础。

3 集对分析与三角模糊数耦合的综合评价模型

3.1 指标体系构建

定子线棒改造技术施工安全设计因素多而复杂，建立统一且全面的安全评价指标体系难度较大。因此，根据相关安全生 产行业标准，并参照大量相关文献[6-7]，结合专家意见以及工程实例，建立了包括作业人员、设备与材料、施工管理、技术因素、环境影响业5个一级指标以及16个二级指标的定子线棒改造施工安全风险评价指标体系[8-10]，如表1所示：

表1 定子线棒改造施工风险评价体系

本文拟对定子线棒改造施工中危险性较大的步骤，包括并头套及接头切割、槽楔退出、线棒拆除、铁心清理、线棒下线、槽楔打入、线棒接头焊接7项工作的风险程度进行评价。

3.2 指标赋权

层次分析法（AHP）法[11]为一种定性定量兼顾的分权方法，其主要步骤是先对问题进行分解，然后按支配关系将其进行分组形成层次结构[14]，接着通过两两比较确定相对重要性，最后结合经验判断，决定各风险因素的总排序。本文结合定子线棒施工风险定性指标较多的实际情况，对安全评价指标划分了层次，而后选用层次分析法量化定性指标并对其进行分权。该方法可以对实际经验进行量化，本文决定采用9级标度，拟用方根法计算权重向量。

3.3 联系度构造

对于分类等级为5的实际不确定性评价问题，可用5元联系数来反映其同、异、反系统结构。不同指标实测值对标准等级的“同、异、反”隶属程度存在差异，相应的联系度表达形式不相同[12]。现以越小越优（即反向指标）来阐述对于评价标准等级Ⅰ（k=1）相应的联系数表达式构建原理。设评价原理n（n=1,2，…，N）等级 k（k=1,2，…，5）的上界限分别为snk，当评价样本指标值小于Ⅰ级标准界限值sn1则定义为同一性，相应的同一度数系数取1；大于Ⅴ级标准界限值sn5则定义为对立性，对立度系数j取-1；而将落入Ⅱ、Ⅲ、Ⅳ级标准界限范围内的定义为差异性，此不确定性需进一步细化。若定义符合Ⅱ级标准定义为偏同差异性，符合Ⅲ级标准定义为中差异性，符合Ⅳ级标准定义为偏反差异度系数，则相应的联系数表达式可构建为：

式中，μpn表示待评样本p的第n个评价指标实测值对评价等级标准I的联系数；spn为样本p评价指标n的实测值。同理可推得效益型指标的表达式为：

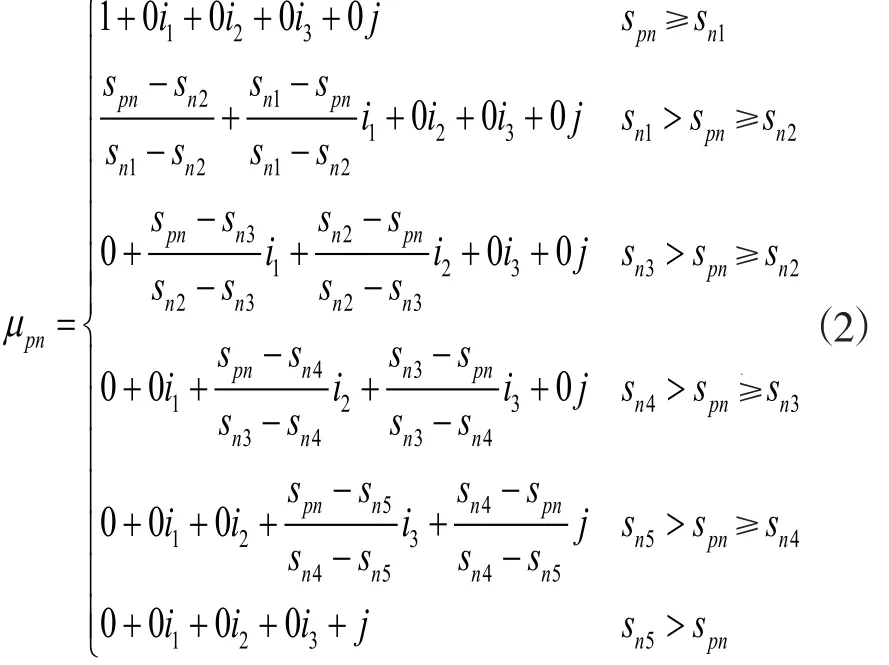
由式（1）和式（2）可知，多元联系数能描述实际问题评价过程中的确定性和不确定性特征,并通过差异度系数实现表示相邻标准等级之间的模糊性,但差异度系数求解一直是集对分析的一个难题,且以往集对分析很少考虑差异度系数取值的模糊性。在此引入分段三角模糊数来分析差异度系数。

若将等级界限值sn2、sn3、和sn4处的差异度系数分别取作i1=0.5、i2=0和i3=-0.5。则其他指标值对应的差异度可按三角模糊数求得:

将式（3）～（5）代入式（1）或（2）。可得联系数

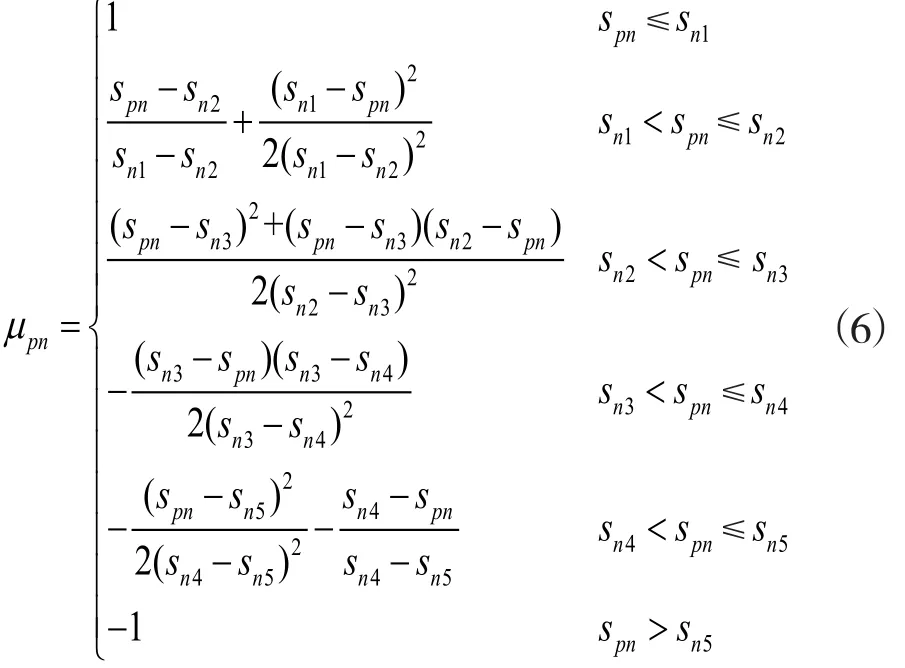
式中符号含义同前说明。

3.4 综合联系度计算与评级

首先根据式（6）计算待评样本p的第n个指标对等级标准的联系数μpn，再结合指标向量ωn计算相应的综合联系数μp，以评定等级，相应的计算模型为

对于等级为5类的综合评价的数学模型为

式中，mp为待评样本的综合联系数的评价等级。

4 实例分析

本文以近尾洲水电站3号机组定子线棒改造项目为例，简述集对分析与三角模糊数耦合风险评价法对定子线棒改造施工风险进行分析与评价的过程，得出评价等级并与实际情况相比较。

4.1 工程资料

近尾洲电厂安装有3台由奥地利制造的灯泡贯流式水轮发电机组，单机容量为21.06 MW。由于电腐蚀的侵害，近尾洲水电站于2017年对3号机组进行定子线棒改造施工，3号机组定子基本参数见表2。

表2 定子基本参数

4.2 模型应用

定子线棒改造施工风险体系的各层指标分别注重于设备安全、危险程度以及措施对风险的影响程度，所以很多指标只能用定性的方法，如安全性、危险性，好与坏来衡量；因此，本文通过参考他人研究成果并结合多名技术骨干的意见，对风险等级按照风险很低、风险较低、风险一般、风险较高、风险很高进行5级分类，如表3所示。并通过专家打分法对定子线棒改造施工风险指标中的各项二级指标进行了评分，结合层次分析法得各指标权重如表4所示。

表4所得分数为根据统计数据所得平均值，每项指标的具体权重皆为利用层次分析法计算结果。接着根据二级指标具体评分以及指标权重求得一级指标评分，如表5所示。

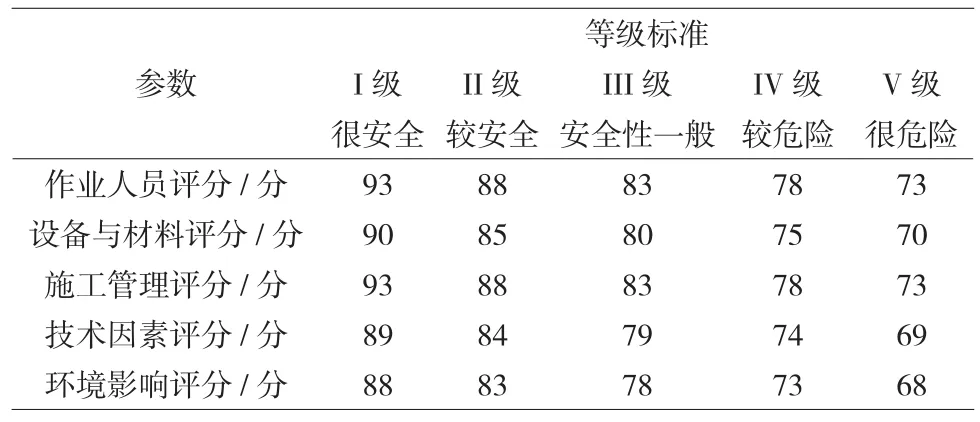
表3

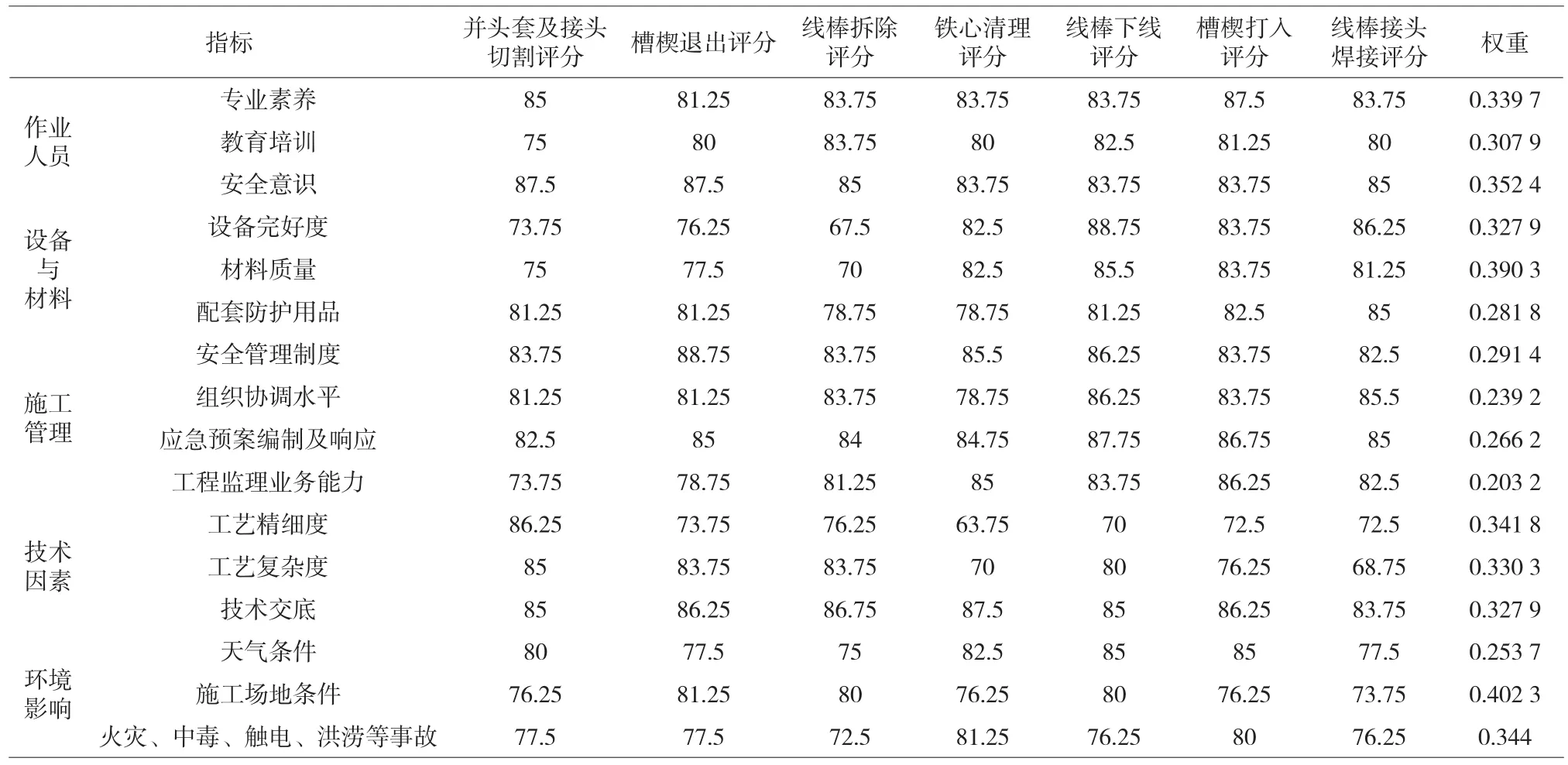
表4

表5

4.3 联系数计算

首先将n个评价指标额样本值组成评价指标集An和第n个评价指标的评价标准集Bn，构成集对H=（An，Bn）。由式（1）～ 式（2）计算得各评价指标样本值的分级联系度计算式，以线棒拆除为例，相应表达见表6。

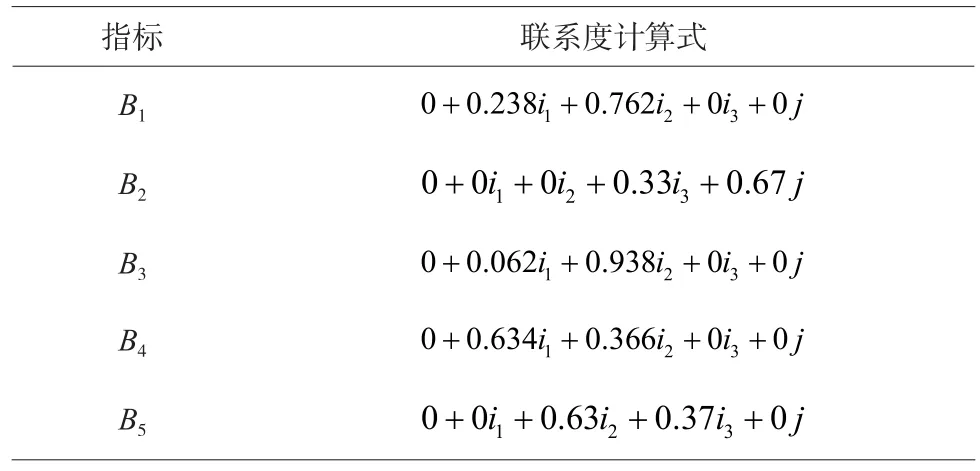
表6

根据表6计算式，分别对并头套及接头切割、槽楔退出、线棒拆除、铁心清理、线棒下线、槽楔打入、线棒接头焊接进行联系度计算，具体过程与前面类似。然后根据式（3）～ 式（5）推论出的式（6），可求得基于三角模糊数的联系数如表7。

4.4 综合联系度计算与评级

根据式（7）和式（8）并结合求得的权重向量ωn得μp和综合联系度如表8。

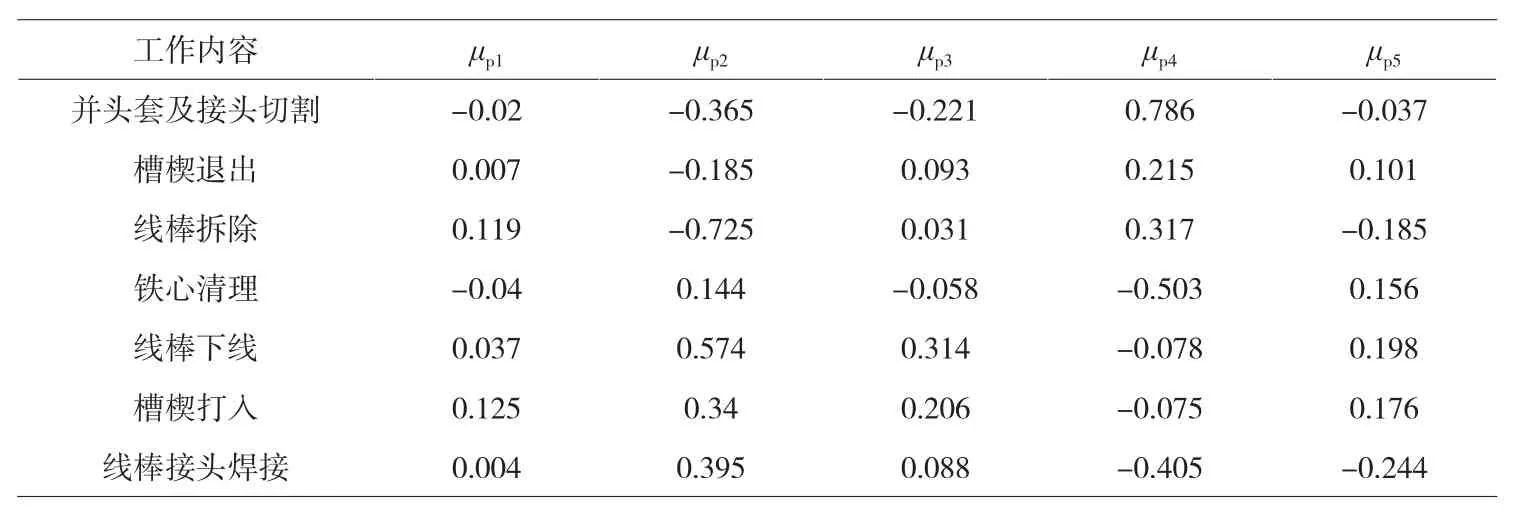
表7

表8

由表7可见，线棒拆除、铁心清理、线棒接头焊接评价等级为3级 （安全性一般），并头套及接头切割、槽楔退出、线棒下线、槽楔打入为2级（较安全），7个步骤的评价结果都为一般及以上，因此表明该项目总体安全性较好，不易出现重大事故。在实际情况中，线棒拆除时易对设备及材料产生损害，波及范围广，损害程度大；铁心清理时因为作业面直接接触铁心及内槽，在清理过程中容易对铁心造成损伤，且清理过程工作量大，工作是否顺利直接影响总工期是否延误；在线棒接头焊接时，由于焊接作业需要专业人员从事，焊接过程要求一定的精细程度，且焊接工作会产生毒烟并属于动火作业，又受工作场地限制易发生火灾、工作人员中毒等事故。由此可见，以上3个工作在施工时需要被重点关注，而本文的评级也将此3个工作评级为3级（安全性一般），可见评价结果与实际情况相符。

5结论

本文先使用集对分析法描述其确定与不确定性，再利用三角模糊数充分体现了差异度系数存在的模糊性和不确定性，然后建立了基于集对分析与三角模糊数耦合模型的定子线棒改造施工风险评价模型。实例应用结果表明，该模型评价思路清晰、运算简便、评价结果精准；同时，该模型将模糊数学知识和集对分析方法有机结合，为集对分析对不确定性的描述提供了一种有效的手段，不仅拓展了模糊数学的应用范围，丰富了集对分析方法，也为定子线棒改造施工风险提供了一种新的评价方法。

参考文献：

[1] Meirong SU, YANG Zhifeng,CHEN Bin. Set pair analysis for urban ecosystem health assessment[J]. Communications in Nonlinear Science and Numerical Simulation, 2009,14(4): 1773-1780.

[2] 李连祥，冯玉国. 基于集对分析联系数的区间型基坑支护方案综合评价方法及其应用[J].数学的实践与认识, 2015, 45(1): 132-138.

[3]葛康，汪明武，陈光怡.基于集对分析与三角模糊数耦合的土壤重金属污染评价模型[J].土壤，2011,43(2):216-220.

[4]王纪鹏，欧阳治华，刘夏临.基于集对分析与三角模糊数的围岩稳定性综合评价模型[J].化工矿物与研究，2013,5(5):20-24.

[5] Cordero C A, Sanz J. Measurement of machinery safety level:European framework for product control-Particular case:Spanish framework for market surveillance[J].Safety Science,2009，47(10): 1285-1296.

[6]田志成.机械安全风险评价[J].中国工程机械学报，2011（9）：367-371.

[7]崔善强.机械安全标准及风险评价的研究[D]. 西安：西安建筑科技大学，2008.

[8]强 跃，何运祥，刘光华. 基于模糊层次分析法的中小型水利水电工程施工风险评价[J]. 施工技术，2013，42(21):51-54.

[9]樊宇,吴晓铭.基于模糊综合评价法的水电工程施工安全评价[J].人民长江，2014，45(24):10-13.

[10]江新,徐平,晋良海,等.水电工程施工疲劳风险分析与量化评价研究[J].长江科学院院报，2016，33(10):149-154.

[11]杜修力,张雪峰,张明聚,等.基于证据理论的深基坑工程施工风险综合评价[J].岩土工程学报，2014,36(1):155-161.

[12]吴开亚,金菊良,潘争伟. 基于三角模糊数截集的联系数模型在城市涝灾影响等级评价中的应用[J].水利学报，2010，41(6):711-719.