2种液体间界面张力的动态测量

后俊明，卢炳鑫，冷雪松，杨知衡，苏 广，王开明

(辽宁科技大学 理学院，辽宁 鞍山 114051)

在一定的温度、压强等条件下，物质以固、液、气三态存在. 各相物质间的接触面统称为界面(约几个分子层厚度)，但通常把气液或气固的界面称为表面. 由于界面上的分子与体相内部的分子所处的环境不同，性质也有差异，因此界面层具有一些特殊的物理和化学性质. 液-液界面是指2种互不混溶或互相饱和的液体所形成的物理界面,而界面张力是描述液-液界面的主要物理量，在表面化学、化工生产、材料制备、石油工业及环境保护等方面有着广泛的应用[1-2]. 目前国内各大高校在物理实验教学中均是测量气液间的液体表面张力系数，测量方法大都以拉脱法为主[3-5]，但在实验过程中存在较多人工测量误差和系统误差，这主要是受到仪器设计结构和实验方法的限制. 代伟、孔维姝等人分别对实验仪器和实验方法进行了改进[6-8]，一定程度上提高了测量精度，但是实验内容依然停留在气液间的液体表面张力系数的测量. 本文利用自制仪器对纯净水和硅油、纯净水和乙酸乙酯所形成的液-液界面张力进行了动态测量. 通过对金属吊环在2种液体的拉脱过程分4个阶段进行了受力分析，建立力平衡方程，求出液膜被拉断前金属吊环所受的最大力及液膜被拉断后金属吊环所受的力，计算出界面张力.

1 实验装置设计

图1为自制2种液体间界面张力的动态实时测量装置图，该仪器主要包括电脑显示器、同步信号转换器、自制实验架台、力敏传感器、金属吊环、恒温杯、温度计、排液孔、排液管、流速调节器和储液槽等组成.

图1 自制实验仪器装置图

与传统的表面张力测量仪器相比较，本实验装置有如下优点：

1)通过同步信号转换器将力敏传感器测量的电压信号转换为数字信号，并在电脑显示器上实时直观显示，并通过嵌套软件在计算机上实时记录电压值，绘制出电压的变化曲线，代替人工记数，从而减小实验测量误差.

2)通过从容器底部缓慢匀速排出液体的方式实现液体与金属吊环之间的拉脱过程，在该过程中金属吊环始终保持水平状态，其平稳性好，避免了用手动调节金属吊环位置变化而引起的测量误差，提高了实验精度. 通过流速调节器可控制从容器底部缓慢匀速排出液体的流速，还可以用来探究液体流速对液-液界面张力的影响，从而找到测量的最佳实验条件.

3)可以控制和检测待测液体的温度. 在测量过程中为了控制待测液体的温度，该装置采用设置有温度计的恒温容器盛放待测液体，既可以读取待测液体的温度值，又能够保持待测液体的温度恒定，从而减小了温度对实验结果的影响.

2 测量方法及分析

2.1 动态测量方法

实验过程： 接通电源，将仪器预热15min； 在传感器横梁端头的小钩上挂砝码盘并进行定标；将金属吊环清洁干净，调平后挂在传感器的小钩上； 实验时，先将吊环置于密度较大的液体Ⅰ中，然后再注入密度较小的液体Ⅱ，调节流速调节器控制从容器底部缓慢匀速排出液体的流速，测量出电压U随时间t的变化曲线. 图2为纯净水和硅油的界面张力测量过程中电压U随时间t的变化曲线.

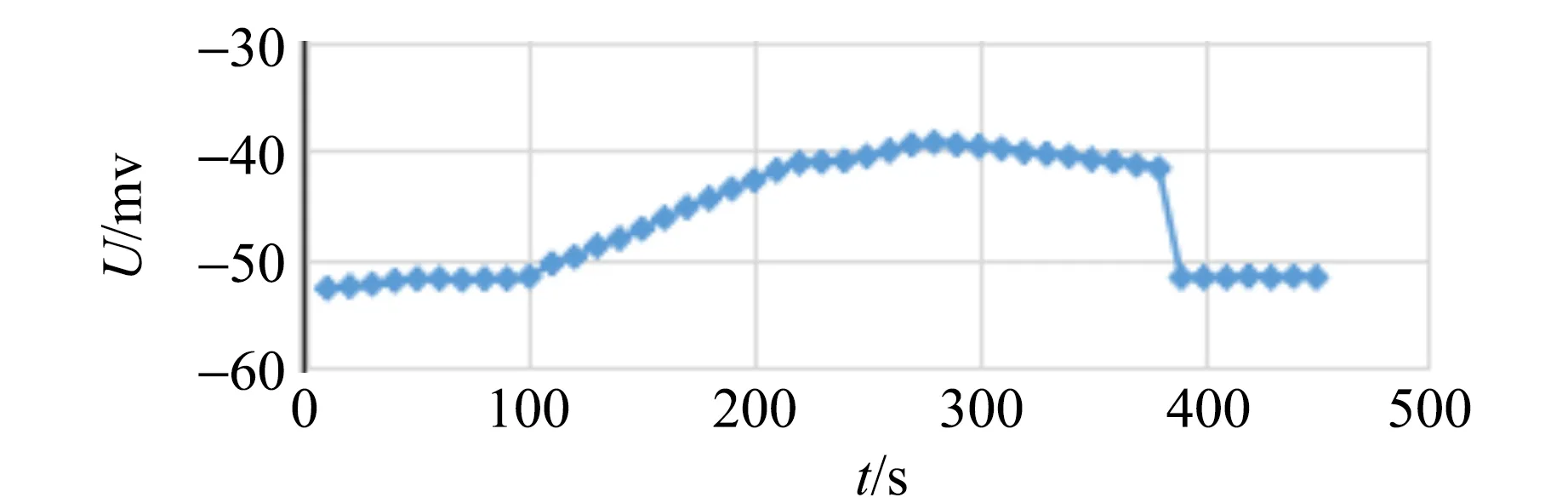
图2 电压U随时间变化曲线

2.2 拉伸过程中吊环的位置及受力分析

实验中吊环由纯净水层拉入硅油层的过程中，对吊环进行受力分析如图3所示.

1) 金属吊环全部浸没在液体Ⅰ中

金属吊环全部浸没在液体Ⅰ中如图3(a)位置所示，此时吊环受到3个力的作用：吊环自身的重力G、液体Ⅰ对吊环的浮力F1Ⅰ以及拉力F1. 在这3个力的作用下金属吊环在液体Ⅰ中匀速上升，力平衡方程为

F1+F1Ⅰ=G,

(1)

其中液体Ⅰ对吊环的浮力为

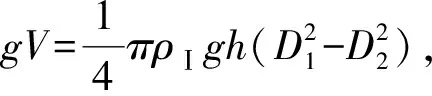
式中，ρⅠ为液体I的密度，h为金属吊环的高度，D1和D2为吊环的外径、内径.

在这一过程中拉力F1恒定，电压表示数不变，与图2中所测数据0～100 s中的数据吻合.

图3 金属吊环位置变化图

2)金属吊环从液体Ⅰ中进入液体Ⅱ中

金属吊环从液体Ⅰ中进入液体Ⅱ中的拉升过程如图3(b)位置所示，吊环在上升的过程中受到4个力的作用，吊环自身的重力G、液体Ⅱ对吊环的浮力F2Ⅱ、液体Ⅰ对吊环的浮力F2Ⅰ以及拉力F2. 在这4个力的作用下吊环匀速上升，力平衡方程为

F2+F2Ⅰ+F2Ⅱ=G,

(2)

其中：

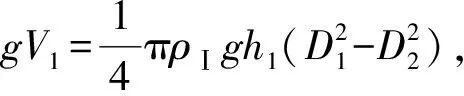
ρⅡ为液体Ⅱ的密度，h=h1+h2，h1和h2分别表示吊环浸在液体Ⅰ和液体Ⅱ中的高度. 整理得：

F2=-k2h1+b2,

(3)

其中：

这一过程中，拉力随金属吊环浸在液体Ⅰ中的高度h1减小而增大，并且成线性关系，对应于图2中100～220 s时间段的电压变化曲线.

3)吊环完全进入液体Ⅱ中

金属吊环完全进入液体Ⅱ拉出液体Ⅰ液膜的过程如图3(c)位置所示. 经过液体Ⅰ、液体Ⅱ界面后吊环继续上升完全进入液体Ⅱ中，在液体Ⅱ中拉起液体Ⅰ的液膜，并且液膜在液体Ⅱ中被拉伸一定距离之后断裂. 该过程中，吊环受到自身重力G、液膜的拉力f、液体Ⅱ对其的浮力F3Ⅱ和拉力F3. 吊环在这4个力的作用下匀速上升，力平衡方程为

F3+F3Ⅱ=G+f′,

(4)

其中

f=αⅠπ(D1+D2)cosθ,

θ表示液膜与竖直方向上的夹角,α1为液体Ⅰ和液体Ⅱ两液体的界面张力. 整理各式得：

F3=k3cosθ+b3,

(5)

其中：

k3=α1π(D1+D2),

对式(5)的中θ角在拉升过程中的变化情况进行讨论：θ角随着拉升的过程逐渐减小，到0以后，由于金属吊环存在一定的厚度，此时液体Ⅰ的液膜并没有被拉断，随着吊环继续被拉升，θ反方向增加；cosθ值先变大，到最大值1后又逐渐变小；此过程拉力F3随着θ的减小而增大，到最大值后再减小[9]，分析结果和图2中220～380 s的数据吻合.

4)液膜断后金属吊环完全浸没在液体Ⅱ中

液膜拉断后金属吊环在液体Ⅱ中继续匀速上升，如图3(d)位置所示. 吊环在上升过程中受到3个力的作用，重力G,液体Ⅱ对吊环的浮力F4Ⅱ和拉力F4，在这3个力的作用下处于平衡状态，力平衡方程为

F4+F4Ⅱ=G,

(6)

其中：

金属吊环这一运动过程中电压值也趋于平稳，对应于图2中380～450 s这一时间段的变化曲线.

3 实验测量结果

实验测量所用金属吊环的外径、内径分别为0.034 96 m和0.033 10 m. 在20 ℃实验条件下，采用自制2种液体间界面张力的动态实时测量仪，测量了纯净水-硅油和纯净水-乙酸乙酯间的界面张力. 测量出金属吊环由液体I中完全进入液体Ⅱ的过程中，液体I的液膜被拉断前电压的最大值U1，拉断后趋于稳定时的电压值为U2，数据结果如表1所示.

表1 2种液体间界面张力的动态实时测量结果

计算出当金属吊环从纯净水到完全进入硅油的过程中,定标k=2.13 mV/N,拉断液膜的力

f=ΔU/k=5.87×10-3N,

故通过该实验装置所测得的纯净水和硅油2种液体的界面张力：α=f/l=27.46×10-3N/m.

计算出当金属吊环从纯净水到完全进入乙酸乙酯的过程中，定标k=3.07 mV/N,拉断液膜的力为

f=ΔU/k=1.50×10-3N,

故通过该实验装置所测得的纯净水和乙酸乙酯2种液体的界面张力：α=f/l=7.01×10-3N/m.

在20 ℃时，纯净水-乙酸乙酯间界面张力的标准值为α0=6.80×10-3N/m[10], 对比实验测量结果，计算出其相对偏差为3.09%.

4 结束语

利用自制仪器测量了纯净水和硅油、纯净水和乙酸乙酯所形成的液-液界面拉断液膜的拉力，进而计算出其界面张力. 采用液体表面张力动态测量装置测量2种液体间界面张力，开拓了测量2种液体间界面张力的途径，且仪器制作成本低、测量方法简单易行.

本实验自制仪器已经申报国家实验新型专利(201721340013.9)

参考文献：

[1] 赵振国. 界面膜原理与应用[M]. 北京：化学工业出版社，2013：78-124.

[2] 曾作祥，孙莉. 界面现象[M]. 上海：华东理工大学出版社，2016：46-76.

[3] 焦丽凤,陆申龙. 用力敏传感器测量液体表面张力系数[J]. 物理实验,2002,22(7):40-42.

[4] 陈骏逸,范伟民. 用硅压阻式力敏传感器测量液体表面张力系数[J]. 实验室研究与探索,2002,21(6):42-44.

[5] 刘升光,王艳辉,牟宗信,等. 拉脱法测液体表面张力系数中的动态演化过程[J]. 物理实验,2017,37(5):12-15.

[6] 代伟,徐平川,陈太红,等. 液体表面张力系数实验装置的改进[J]. 大学物理,2011,30(9):38-40.

[7] 孔维姝,赵维金,唐延林,等. 拉脱法测量液体表面张力系数实验的改进[J]. 物理实验，2012，32(1):36-38.

[8] 郑晓慧,袁晓梅,唐卫红. 可控温液体表面张力系数测定仪的设计与制作[J]. 物理实验，2015，35(11):24-28.

[9] 郑经学,冷雪松,王天前,等. 液体表面张力系数测量的分析[J]. 大学物理实验,2017,30(5):74-77.

[10] 孙艳辉，何广平，马国正,等. 物理化学实用手册[M]. 北京：化学工业出版社，2016：630.