基于垂直镜面RCS减缩的周期结构弯曲性能探究及设计*

王利云，张国瑞，周佩珩

（电子科技大学 电子科学与工程学院 国家电磁辐射控制材料工程技术研究中心，四川 成都 610000）

0 引 言

随着科学技术的发展，军事、民用设备和系统的自动化、电子化水平不断提高，电磁环境日趋复杂。RCS减缩作为提高目标生存能力和突防能力的有效手段，是世界各国重点开发的技术[1-3]。

目前，超材料技术越来越多地应用于RCS减缩领域。文献[4-6]把超材料加载于微带天线贴片周围，实现了天线RCS减缩；文献[7-8]研究了超材料在波导缝隙天线RCS减缩中的作用。国内外研究大量集中在平面目标的RCS减缩上，随着技术的发展，要求超材料能够灵活加载于特殊外形的目标体，而简单均匀结构超材料加载到曲面上会出现减缩性能不稳定的问题。目前，曲面RCS减缩主要依赖于复杂渐变单元图形[9-10]，基于遗传算法，通过大量的计算、优化，设计出复杂的渐变图形，存在较大的设计、制作困难。在众多超材料中，平面型周期结构由于简单结构、性能优良而受到各国科研工作者的广泛关注[11-12]。这种结构由周期性导电图案、介质层和金属底板构成，可以通过调节形状和尺寸参数，获得所需工作频段内的特殊性能。本文主要探究了正方形周期结构在弯曲状态下、电磁波垂直入射情况下的RCS性能变化趋势，初步总结了弯曲状态下正方形周期结构RCS的性能变化规律及其原因，并提出了一种在弯曲状态下保持RCS性能相对稳定的方环周期结构。

1 主要原理

定量描述目标散射强弱的物理量是目标对入射雷达波呈现的有效散射截面积，通常简称为目标的雷达散射截面或者雷达截面（Radar Cross Section）。它是目标的一种假象面积，一般用符号σ表示，单位为m2。雷达散射截面可表示为：

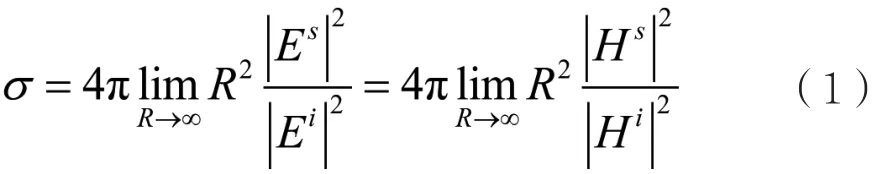
式中Ei、Hi分别表示入射雷达波在目标处的电磁场强度，Es、Hs表示目标散射波在雷达处的电磁场强度，R为目标到雷达天线的距离。当距离R趋于无穷大时，能够满足远场条件，此时照射在目标体上的雷达入射波和雷达处的散射波可近似于平面波。

为了便于理解和计算，雷达散射截面积用式（2）表示，单位为dBsm：

本文主要探究了弯曲目标体的单站RCS，因此对于目标体在某一频率对入射电磁波的RCS减缩值，用加载周期结构材料后的该频率单站RCS值减去该频率PEC的单站RCS值表征，即：

这里假定目标体为圆柱体上对应一定弧度的曲面，用边缘处切线与水平面的夹角θ来定义目标体的弯曲程度，如图1所示。

图1 目标体弯曲程度示意

2 设计仿真

本文主要对正方形、方环两种周期结构进行了弯曲状态下RCS减缩性能和斜入射电场分布的仿真。利用CST仿真软件对上述两种结构进行仿真，结构如图2所示。上层为导电图案，中间为介质层，底层为连续完美电导体（PEC）。结构周期p=15 mm，图案尺寸l1=9 mm，l2=14 mm，b=8 mm，介质层材料为硅橡胶，相对介电常数为3.3，损耗角正切为0.007 6，相对磁导率为1，厚度为3 mm，方阻R1=130 Ω，R2=50 Ω。

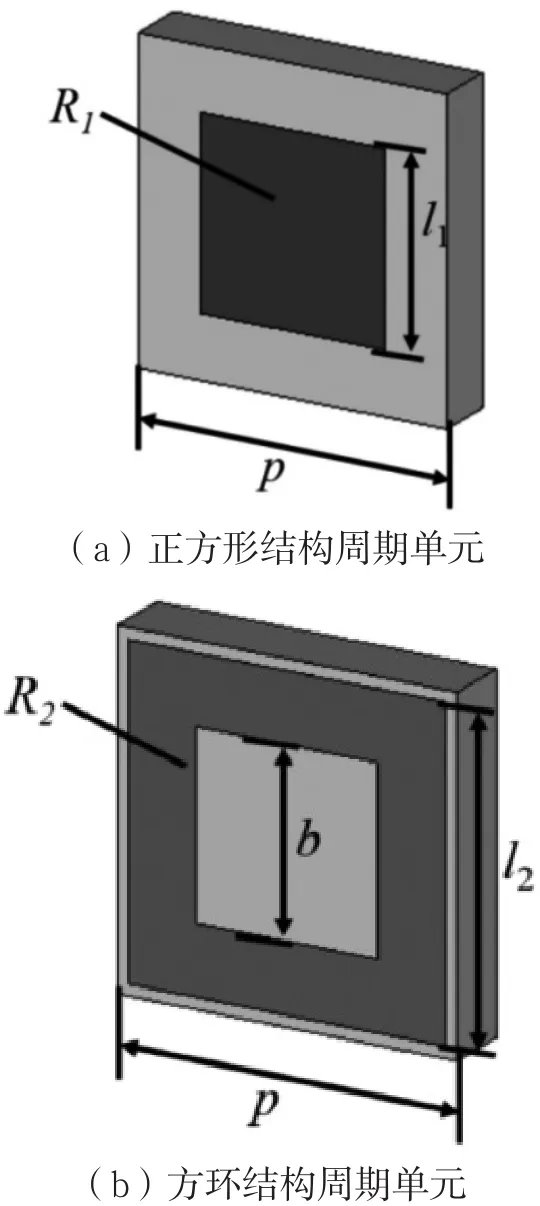
图2 仿真结构周期单元

电磁波入射到弯曲目标体上，可近似通过结构单元斜入射情况来进行分析。如图3所示，斜入射情况下，由于曲面不同位置电磁波到达结构表面存在路程差，导致图案层电场分布与垂直入射电场分布存在差异。

图3 电磁波斜入射示意

图4 、图5分别为正方形周期结构在TE、TM极化方式下不同弯曲程度的△RCS曲线。可以看到，正方形结构在未弯曲时的有效带宽为9.5～16.4 GHz；在TE波入射下，当弯曲角度为10°时，对电磁波的RCS减缩几乎全部降低到-10 dB以下，仅在10 GHz左右减缩值达到-10 dB；随着弯曲程度的不断增加，减缩效果不断变差，在很窄的频段内减缩值达到-10 dB以上。TM波入射情况下也是如此，当弯曲角度为10°时，14.2～16.5 GHz内减缩值可达到-10 dB；弯曲角度增加后，减缩效果变差。

图4 正方形结构TE极化方式下不同弯曲程度△RCS曲线

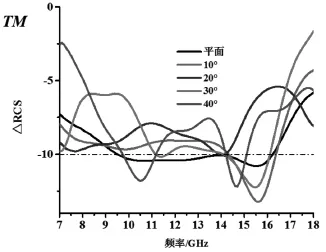
图5 正方形结构TM极化方式下不同弯曲程度△RCS曲线

图6 为CST软件中正方形结构在垂直入射和斜入射情况下谐振点的电场分布图。可以看出，垂直入射下，电场集中在图案层的边缘处。TE波斜入射时，电场主要集中在图案的4个角，且强度也存在差异。TM波斜入射时，电场主要集中在图案层的一端，且相邻单元边缘没有电荷聚集。电场的这种不均匀分布破坏了原有的谐振条件，造成了二次散射，使得正方形结构在斜入射或弯曲状态下的RCS减缩性能变差。

图6 正方形结构在垂直入射和斜入射情况下谐振点的电场分布

图7、图8分别为方环结构在TE、TM极化方式下不同弯曲程度的△RCS曲线。可以看到，开口环结构在未弯曲时，在10.4～16.4 GHz RCS减缩可达到-10 dB以上；在TE波入射下，当弯曲角度为10°和20°时，在原频段内仍可保持-10 dB以上的减缩；弯曲角增加到30°、40°时，带宽略有减小。TM波入射下，10°弯曲角减缩保持稳定；随着弯曲角度的增加，带宽略有减小，但总体性能保持稳定。为了更好地体现结构的减缩性能，选取PEC与方环结构在TE极化波和TM极化波入射下11.9 GHz处双站RCS对比曲线，如图9所示。从曲线可以看出，不论是TE极化波还是TM极化波，在5°～175°RCS减缩都能达到-10 dB以上。

图7 方环结构TE极化方式下不同弯曲程度△RCS曲线

图8 方环结构TM极化方式下不同弯曲程度△RCS曲线

图10 （a）为设计的方环结构在垂直入射情况下的表面电流分布图。可以看到，方环结构的表面电流并非沿着平行于电场方向的边，而是在垂直于入射波电场方向的边。感生电场主要集中在图案的边缘，图10（b）、图10（c）和图10（d）为CST软件中方环结构在斜入射情况下谐振点的电场分布图。TE和TM波斜入射时，电场分布与垂直入射大致相同，集中在图案边缘，使得方环结构在斜入射或弯曲状态下的RCS减缩性能稳定。

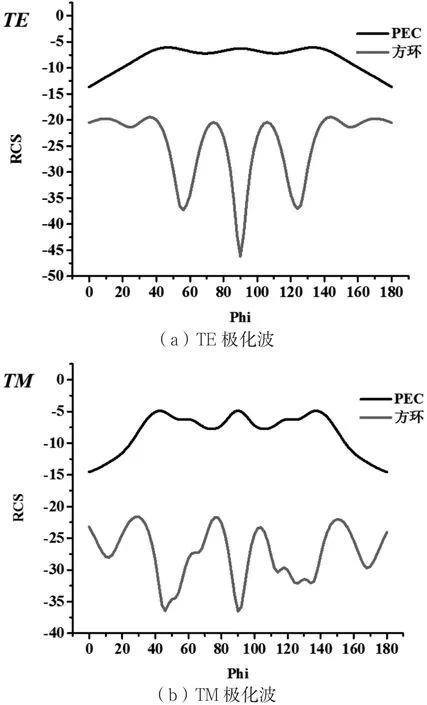
图9 PEC与方环结构在TE极化波和TM极化波入射下11.9 GHz处的双站RCS对比曲线

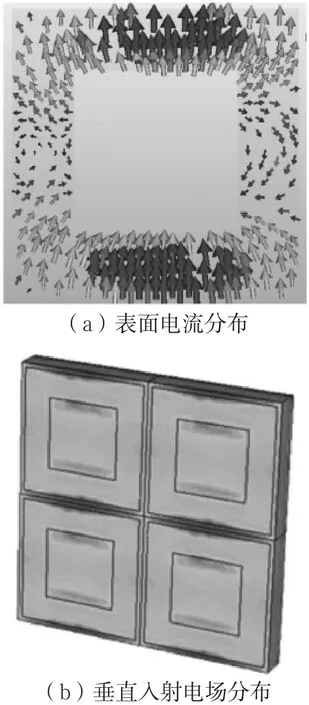
图10 方环结构在垂直入射和斜入射情况下谐振点的表面电流和电场分布

3 结 语

本文利用CST软件对正方形和方环结构在垂直入射、斜入射场分布以及不同弯曲程度下的RCS减缩进行对比分析，发现正方形结构在斜入射或弯曲状态下由于同相位面的电磁波到达结构表面存在路程差，导致场分布不均匀，破坏了原有的谐振条件而造成二次散射，致使减缩效果变差。而设计的方环结构在斜入射或弯曲状态下场分布与垂直入射时大致相同，分别在TE、TM两种极化波入射下，在11.7～15.4 GHz可以保证-10 dB以上的RCS减缩，使得结构在斜入射或弯曲状态下减缩效果稳定。

参考文献：

[1] 周禹龙,曹祥玉,高军等.双频频率选择表面及其在微带天线宽带RCS减缩中的应用[J].电子与信息学报 ,2017,39(06)：1446-1451.ZHOU Yu-long,CAO Xiang-yu,GAO Jun,et al.Dual Frequency Selective Surface and Its Application in Wideband RCS Reduction of Microstrip Antennas[J].Journal of Electronics & Information Technolo gy,2017,39(06)：1446-1451.

[2] 张晨,曹祥玉,高军等.低RCS宽带磁电偶极子贴片天线设计[J].电子与信息学报,2016,38(04)：1012-1016.ZHANG Chen,CAO Xiang-yu,GAO Jun,et al.Design of Low RCS Wideband Magnetic Dipole Patch Antenna[J].Journal of Electronics and Information Technolo gy,2016,38(04)：1012-1016.

[3] Pan W B,Huang C,Chen P,et al.A Low-RCS and High-gain Partially Reflecting Surface Antenna[J].IEEE Transactions on Antennas and Propagati on,2014,62(02)：945-949.

[4] 杨欢欢,曹祥玉,高军等.基于超材料吸波体的低雷达散射截面微带天线设计[J].物理学报 ,2013,62(06)：064103.YANG Huan-huan,CAO Xiang-yu,GAO Jun,et al.Low Radar Cross Section Microstrip Antenna Design Based on Absorbers of Metamaterials[J].Chinese Journal of Physics,2013,62(06)：064103.

[5] 张浩,曹祥玉,高军等.基于分形的吸波材料及其在微带天线中的应用[J].微波学报,2013,29(04)：57-61.ZHANG Hao,CAO Xiang-yu,GAO Jun,et al.Fractalbased Wave-absorbing Material and Its Application in Microstrip Antenna[J].Chinese Journal of Microwaves,2013,29(04)：57-61.

[6] 商楷,曹祥玉,高军等.分形吸波体设计及其在微带天线中的应用[J].现代雷达,2013,35(06)：54-57.SHANG Kai,CAO Xiang-yu,GAO Jun,et al.Fractal Absorber Design and Its Application in Microstrip Antenna[J].Modern Radar,2013,35(06)：54-57.

[7] 杨欢欢,曹祥玉,高军等.一种超薄吸波材料及其在缝隙天线中的应用[J].电子与信息学报 ,2012,34(11)：2790-2794.YANG Huan-huan,CAO Xiang-yu,GAO Jun,et al.An Ultra-thin Absorbing Material and Its Application in Slot Antennas[J].Journal of Electronics and Information Tech nology,2012,34(11)：2790-2794.

[8] 刘涛,曹祥玉,高军等.基于超材料的吸波体设计及其波导缝隙天线应用[J].物理学报,2012,61(18)：184101.LIU Tao,CAO Xiang-yu,GAO Jun,et al.Absorber Design Based on Metamaterials and Its Waveguide Slot Antenna Application[J].Chinese Journal of Physics,2012,61(18)：184101.

[9] Chen W,Balanis C A,Birtcher C R,et al.Cylindrically Curved Checkerboard Surfaces for Radar Cross-Section Reduction[J].IEEE Antennas and Wireless Propagation Letters,2018,17(02)：343-346.

[10] Shahi A,Abdolali A.Cylinder Scattering Pattern Manipulation for Dual-Polarized Radar Cross-section Reduction Using Inhomogeneous Metasurface[C].Electrical Engineering(ICEE),2017 Iranian Conference on IEEE,2017：1691-1696.

[11] Landy N I,Sajuyigbe S,Mock J J,et al.Perfect Metamaterial Absorber[J].Physical Review Letters,2008,100(20)：207402.

[12] Boyko S N,Kukharenko A S,Yaskin Y S.EBG Metamaterial Ground Plane for Mitigation of Multipath Signals in GNSS Antenna[J].Journal of Electromagnetic Engineering and Science,2015,15(04)：199-205.