基于PSO优化LS-SVM算法的网络空间态势预测研究*

陈维鹏，敖志刚，屠义强，郭 杰，叶春雷，童 俊

（1.陆军工程大学 野战工程学院，江苏 南京 210007；2.中国人民解放军73233部队，浙江 舟山 316014）

0 引 言

对于非线性模型标定，文献[1-3]采取的方法主要有神经网络方法和遗传算法。神经网络方法虽然能够以任意精度逼近任何非线性关系，但它基于经验风险最小化原则，泛化能力有限，容易得到局部极小值。遗传算法是一种高度并行性全局搜索算法，但非线性标定参数较多，使得交叉、变异等遗传操作复杂，运行时间较长，且在接近最优解时收敛缓慢甚至停滞。支持向量机的概念最初由贝尔实验室提出，利用多维统计预测理论[4]解决机器学习问题。SVM是神经网络领域最重要的研究方向之一，在手写识别、人脸检测、生物信息和数据挖掘[5]等领域有着广泛应用。它基于结构风险最小化原则，泛化能力强，且能得到唯一全局最优解[6]。根据SVM的优点，结合网络空间态势变化表现出的高度非线性[7]、时变和不确定性的特点，可以发现，在SVM中也很适合预测网络空间的作战态势。所以，提出了一种基于SVM的态势预测方法。LS-SVM是标准SVM的一种改进，能够大大提高求解速度。为了预测数据的准确性，PSO用于优化SVM。

1 粒子群优化的最小二乘支持向量机

1.1 最小二乘支持向量机回归算法

LS-SVM是一种二次损失函数下的SVM[8]。LS-SVM将不等式约束转化为等式约束，求解原始SVM算法线性方程组的解，降低了难度。因此，选取分类器LS-SVM用来估计未知函数：

其中，∈Rn，y∈Rn，非线性函数φ(⋅)将输入k值转换为特征值 Rn→Rnh，权重向量wT和常值偏差b为带求解的量。

给定训练集{xk,yk}，LS-SVM定义如下：

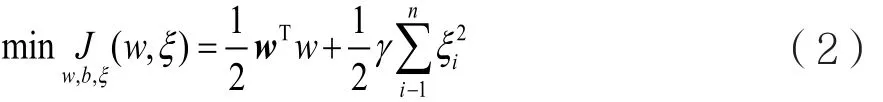
其中 γ ∈ Rn，ξ为分类器校正后的精度误差，满足以下条件：

相应的拉格朗日函数为：

Karush-Kuhn-Tucker（KKT）优化条件为：

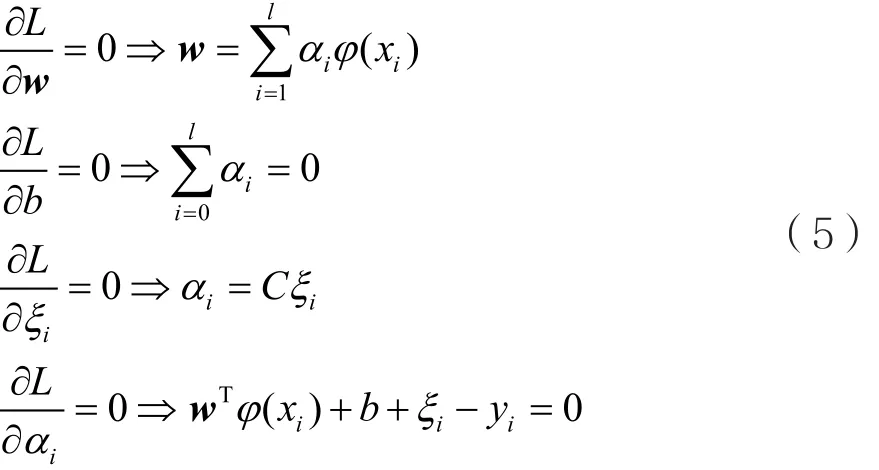
消去w和ξ，得到如下方程：

其中，y = [y1, y2,…,yl]T，A = [1,1,… ,1 ]T（l个1），α= [ α1, α2,… αl]T，方阵 Ω 的元素是 Ωij=K(xi,yi)核函数。RBF函数为核函数，即：

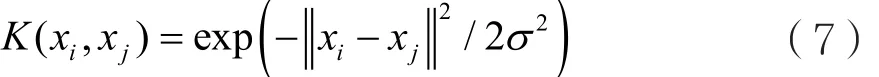
LS-SVM的预测模型为：

1.2 改进的PSO算法

N维空间中，假定有种群 x ={x1,x2,…,xm}[9]。某i粒子包含2个n维向量：一个是粒子位置属性；一个是粒子速度属性。首先，粒子群数据初始化为随机解，通过共享最优数据进行搜索，迭代后得到最优解。PSO算法研究发现，如果参数存在误差，粒子群可能会错过最优解；而在收敛的情况下，最优解精度不高。针对以上不足，本文采用改变惯性、主导、收敛和调整参数等措施，得到了改进的粒子群优化模型式（9）和式（10）。迭代中，粒子会比较状态最优解 pbest和全局最优解 gbest。具体地，根据下列方程调整粒子i在迭代时的状态：

方程参数设置见表2。其中， c1和 r1是取值为[1，2]的加速因子； r1和 r2是均匀分布在[0，1]区间上的2个独立的伪随机数； vi∈[- vmax,vmax](vmax是设定常数)；β是收敛因子；ω是惯性因子，其值为[0，1]，有 ω =ωmax-(ωmax-ωmin)t/Tmax（t和 Tmax分别当前和最大迭代次数），可在迭代过程中自适应调整大小。当增加迭代次数时，ω值减少，则优化快速精准；α是引导因子，有 α = k +rand(⋅)，0.1≤k≤1.0，而rand(⋅)是[0，1]上的随机数，用来逼近最优解；微调因子ε=10-4rand(·)，可为避免出现粒子趋同加以调节。

1.3 基于PSO算法的LS-SVM参数寻优

LS-SVM模型的惩罚因子c对实验误差和泛化能力[10]有很大影响。不同的核函数可以构造不同的支持向量机。核函数分为多项式核函数、Sigmoid核函数和径向基核函数[11]。其中，径向基核函数是应用最广泛的核函数，而核函数参数σ的选择直接影响SVM算法的复杂度[12]。总之，惩罚因子c和核函数参数σ影响LS-SVM模型的性能，所以是否选择最优，对模型的精度有很大影响[13]。PSO算法优化惩罚因子c和核函数参数σ。

1.4 PSO优化LS-SVM算法

算法实现，如图1所示。

图1 LS-SVM算法的PSO优化过程

步骤1：粒子群参数初始化，包括设定粒子群数n、群体规模n、迭代次数T、粒子矢量参数x = (γ , δ2)、粒子位置属性γ和粒子速度属性 δ2。

步骤2：粒子当前速度比其经历过的最好位置pbest所对应的适应度小，则将阿奇作为当前最好的位置 pbest。

步骤3：粒子经历过的最好位置 pbest对应的适应度比全局最优位置 gbest对应的适应度小，则粒子当前最优位置为 gbest。

步骤4：根据式（9）和式（10）变化粒子的速度vi+1和 xi+1，产生新种群 x ( t+1)。

步骤5：判断是否满足终止条件（if t ＞ Tmax），如满足，则输出当前值；否则，t = t+1，跳到步骤2，继续新一轮优化。

步骤6：获得最优粒子信息，赋予LS-SVM模型。

2 PSO优化LS-SVM算法预测模型

首先，构建网络空间态势样本，网络空间态势值如同时间序列[14]。网络空间状态值是一个非线性时间序列{xi}={x1, x2,…,xn}，非线性预测时间序列的安全形势主要是看安全态势值 i + p和p时刻安全态势值 xi, xi+1, … ,xi+p-1之间的关系，即：

其中f是表示时间序列非线性关系的函数。根据SVM理论，上述非线性对应关系可以学习已知安全态势时间序列样本[15]。

PSO算法和LS-SVM算法是基于滑动窗口动态生成的。假设已知时间监测点1,2,…n对应的网络态势值分别为 a1, a2,… ,an，设定窗口大小为m，则第1条样本记录为 a1, a2,… ,am。因此，预测 m +1次监测点的网络态势值 am+1，然后构造样本记录a2,a3,… ,am+1，并预测 m + 2时间监测点的网络态势值 am+2等。m为3，即滑动窗口大小为3。为了防止预测误差的累积，假设当前的安全态势预测模型预测时间点t态势值。如果根据实际情况计算之前的时间点 t - k 态势值，则时间点t的预测值为实际态势值。

基于PSO优化的LS-SVM算法网络空间态势预测模型，如图2所示。

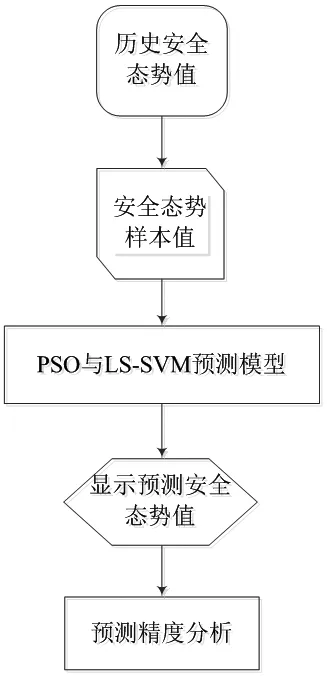
图2 基于PSO优化LS-SVM算法的预测模型流程

步骤1：通过模型评估得到态势值。

步骤2：根据时间序列法生成数据集，将样本集划分为训练样本集和测试样本集。训练样本集通过SVM训练得到初始预测模型，预测样本集用于检测初始预测模型的准确性。以开放式测试的形式作为训练集和测试集，尽可能保证两者的独立性。

步骤3：训练样本被输入到PSO优化LS-SVM算法模型，并使用优化算法搜索SVM的最佳训练参数。

步骤4：输入测试样本到模型进行预测。

步骤5：预测模型精确度分析比较。

3 仿真实验与结果分析

3.1 实验环境组建

本实验利用VMware Worlstation for Win64软件构建虚拟蜜网Honeynet仿真真实环境、提取数据，并应用Matlab软件实现标准BP和改进后的算法，仿真实验环境如图3所示。

图3 Honeynet网络拓扑

具体如下：

操作系统：Windows（Matlab）+RedHat Linux 9.0

Matlab版本：Matlab R2012a

CPU及内存：2.40 GHz×2，4 GB

软件配置包括：VMware Worlstation for Win64，VMware-worlstation-full-7.0.0-203739；蜜网网关虚拟机Roo Honeywall CDROM v1.4。

具体步骤包括：蜜罐机（honeypot）的安装与配置；虚拟蜜网网关机（Honeywall）的搭建与配置；sebel安装；登陆Honeywall（My SQL）数据库；收集信息。图4为虚拟蜜网安装的主界面。

图4 Honeynet安装界面

3.2 态势数据提取

数据采集并经过事件校准后得到事件。时间校准后每个事件都有属性，部分属性说明如表1所示。其中，对于非数值型属性，在实验仿真中采用不同方法转换成数值型，其他属性还有访问文件、注册和服务配置信息等。

表1 事件属性及对应表示形式

3.3 实验分析

本章的实验数据来源于Honeynet技术测试结果，并进行相关数据提取，得到100组数据（见图5、图6）。以其中80个数据作为学习样本，20个数据作为训练样本。用Matlab编写实验程序，采用LS-SVM lab 1.5版分类器。

图5 nmap扫描测试实验

图6 漏洞扫描实验

3.3.1 实验过程

（1）样本特征选取与归一化处理。由于参数大小、量级不同，需将数据进行[0，1]归一化：

其中，样本输入输出值x、y；样本最大值、最小值为maxx 、minx 。

（2）仿真计算与分析。首先逐渐增加阶数为5（输入变量4、输出变量1），重构网络空间态势序列，生成SVM的训练和测试样本，并改进PSO算法进行迭代寻优。设置粒子群搜索参数初始值，如表2所示。

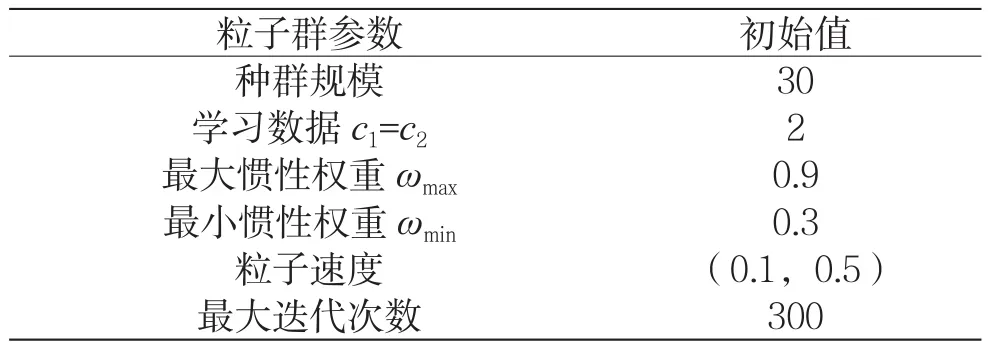
表2 粒子群参数初始值

根据PSO优化LS-SVM算法预测模型对数据集中的20个态势值进行预测，得到如图7所示的结果。

图7 网络空间态势感知部分数据集的PSO优化LS-SVM算法预测值与实际值比较

3.3.2 结果分析

为了验证改进算法的预测精度，利用现有网络空间态势预测的PSO优化LS-SVM算法、GA-SVM以及SVM进行同样的实验比较，得到如图8所示的结果。

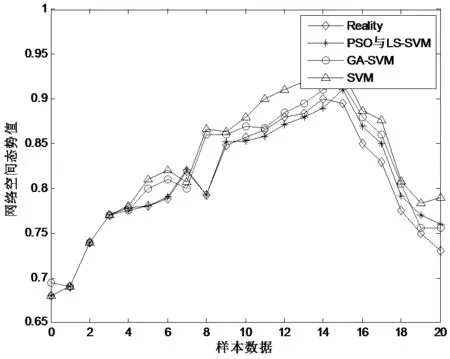
图8 三种算法态势预测曲值对比

为了验证PSO算法和LS-SVM模型的优势，以均方根误差（RMSE）和平均绝对误差率（MAPE）作为评价指标[16]：

传统的SVM模型容易陷入局部最优；GA-SVM结果接近粒子群优化的LS-SVM算法，但遗传算法比粒子群算法收敛复杂，计算误差也相对较大。从图8的实验结果可以看出，采用粒子群优化的LS-SVM预测方法的真实值偏差最小，更接近实际，见图9。

图9 三种算法态势预测曲值绝对误差对比

表2中SVM算法均方根误差为3.402 1，绝对误差率为13.45%；GA优化SVM算法均方根误差为2.473 8，绝对误差率为3.93%；PSO-LSSVM算法均方根误差为1.1，绝对误差率为0.66%。因此，我们可以得出PSO优化LS-SVM算法精度最高，效果最好。

4 结 语

考虑到网络空间态势值呈线性，而BP神经网络算法存在解决小样本局限、容易陷入局部极小值、收敛速度慢等缺点，利用SVM非线性处理小样本数据，建立了非线性拟合模型，提出了一种将LS-SVM和PSO算法相结合的新的快速全局优化和非线性拟合，即基于网络空间态势感知的PSO优化LS-SVM算法。与传统方法比较，基于粒子群优化的LS-SVM算法较传统SVM算法、遗传算法优化的SVM算法，在预测精度上更好，满足了实验要求。

参考文献：

[1] Bopche G S,Mehtre B M.Attack Graph Generation,Visualization and Analysis：Issues and Challenges[C].Proc. of Second International Symposium,2014：379-390.[2] Snidaro L,Visentini I,Bryan K.Fusing Uncertain Knowledge and Evidence for Maritime Situational Awareness Via Markov Logic Networks[J].Information Fusion,2015(21)：159-172.

[3] Endsley M R.Final Reflections：Situation Awareness Models and Measure[J].Journal of Cognitive Engineering and Decision Making,2015,9(01)：101-111.

[4] Aleroud A,Karabatis G,Sharma P,et al.Context and Semantics for Detection of Cyber Attacks[J].Int’l Journal of Information & Computer Security,2014,6(01)：63-92.

[5] Alan N S,Christopher L B,Franklin E W.Revisions to the JDL Data Fusion Model[C].Proc Third NATO/IRIS Conferenee,1998：430-44l.

[6] Soleimani M,Ghorbani A A.Multi-Layer Episode Filtering for the Multi-step Attack Detection[J].Computer Communications,2012,35(11)：1368-1379.

[7] Liu X W,Wang H Q,Lü H W,et al.Fusion-Based Cognitive Awareness-control Model for Network Security Situation[J].Journal of Software,2016,27(08)：2099-2114.

[8] Sadighian A,Fernandez J M,Lemay A,et al.ONTIDS a Highly Flexible Context-aware and Ontology-based Alert Correlation Framework[C].Proc. of the Revised Selected Papers of Int’l Symp.on Foundations & Practice of Security,2013：161-177.

[9] Sadighian A,Zargar S T,Fernandez J M,Lemay A.Semantic-Based Context-aware Alert Fusion for Distributed Intrusion Detection Systems[C].Proc. of the 2013 Int’l Conf.on Risks and Security of Internet and Systems,2013：1-6.

[10] Yan G,Lee R,Kent A,et al.Towards a Bayesian Network Game Framework for Evaluating DDoS Attacks and Defense[C].Proc. of the ACM Conf. on Computer &Communications Security,2012：553-566.

[11] 飞思科技.神经网络理论和matlab7实现[M].北京：电子工业出版社,2016：15-30.FECIT Technological.Neural Network Theory and MATLAB7 Implementation[M].Beijing：Electronic Industry Press,2016：15-30.

[12] 李捷,刘瑞新,刘先省等.一种基于混合模型的实时网络流量预测算法[J].计算机研究与发展 ,2006,43(05)：806-812.LI Jie,LIU Rui-xin,LIU Xian-sheng,et al.A Realtime Network Traffic Prediction Algorithm Based on Hybrid Model[J].Computer Research and Developme nt,2006,43(05)：806-812.

[13] 谢丽霞,王亚超,于巾博.基于神经网络的网络安全态势感知[J].清华大学学报,2013,53(12)：1750-1760.XIE Li-xia,WANG Ya-chao,YU Jin-bo.Network Security Situational Awareness Based on Neural Network[J].Journal of Tsinghua University,2013,53(12)：1750-1760.

[14] 任帅,慕德俊,张弢等.信息安全风险评估方法研究[J].信息安全与通信保密,2009(02)：54-56.REN Shuai,MU De-jun,ZHANG Tao,et al.Research on Risk Assessment Method of Information Security[J].Information Security and Communication Secrecy,2009(02)：54-56.

[15] 宣蕾.网络安全定量风险评估及预测技术研究[D].长沙：国防科学技术大学,2007.XUAN Lei.Research on Quantitative Risk Assessment and Prediction Technology of Network Security[D].Changsha：National University of Defense Science and Technology,2007.

[16] 王宇飞,沈红岩.基于改进广义回归神经网络的网络安全态势预测[J].华北电力大学学报,2011,38(03)：91-95.WANG Yu-fei,SHEN Hong-yan.Network Security Situation Prediction Based on Improved Generalized Regression Neural Network[J].Journal of North China Electric Power University,2011,38(03)：91-95.