半监督模糊聚类算法的研究与改进*

白福均，高建瓴，宋文慧，贺思云

（贵州大学 大数据与信息工程学院，贵州 贵阳 550025）

0 引 言

半监督学习是机器学习与模式识别学科中的研究热点。本质上来说，它的实质是介于监督学习和无监督学习之间的一种学习方式。根据学习内容，它可以分成三类：半监督聚类、半监督分类以及半监督回归[1-2]。其中，半监督聚类的本质是在少量先验信息的帮助下去引导无监督的聚类过程，从而提高聚类算法的精度。1985年，Pedrycz[3]在研究模糊聚类算法的时候，已经提出了半监督聚类，不过在那时被称作“部分监督”[4]（Partial Supervision）。然而，近几年，伴随着实际应用中的问题规模越来越大，半监督聚类算法再次回归到学者研究热门领域中，很多经典的聚类算法被不断引申到“半监督”版本。Blum& Mitchell、Joachims等人提出，当待聚类的数据集中含有少量的标记数据但无法完全分布到所有类别时，可以采用部分的标记信息去引导整个无监督的算法进程，从而提升聚类的准确度[5]。

一般来说，半监督聚类中的先验信息通过相关行业专家的专业知识得到，可以分成两大类，即类别标记信息和约束信息。类别标记信息是指在还没有进行聚类时就已经知道了某个数据对象的类别，而约束信息则在实际生活中最常见，是指根据常识可以清楚知道某两个数据对象是否属于同一类。2000年，Wagstaff提出使用must-Link（正关联）和cannot-Link（负关联）来形容这种关系[6]。

鉴于半监督聚类可以有效地使用先验信息，从而能够取得更好的聚类结果，很多国内外学者都进行了比较深入的探索和学习，也提出了一些代表性算法，如Cop-Kmeans算法[7]、CKS算法[8]、Seeded-Kmeans算法[7]和SAP算法[9]等，也都取得了不错的聚类效果。

可是，在实际应用中，虽然可以获得含有先验信息的数据，但是由于先验信息的获取需要消耗一定的人力、财力以及物力，导致含有先验信息的数据在整个数据集中所占的比重很小，使得半监督聚类算法不能充分有效地利用先验信息指导整个聚类过程，导致最终的聚类结果不是很理想。

本文在对模糊C均值聚类（FCM）算法和半监督模糊C均值聚类（SFCM）算法研究的基础上，提出通过调节监督信息比重来改进SFCM算法——SSFCM算法，使之在先验信息稀少时，SFCM算法仍然可以充分有效地利用先验信 息，提高聚类性能。

1 半监督模糊C均值聚类算法

1.1 模糊C均值聚类算法

1.1.1 FCM算法的基本思想

FCM算法[10-12]是理论知识最为完善的算法之一，在实际应用中也很常见。从本质上来讲，它属于基于划分算法的范畴，但它是一种柔性的模糊划分，是在聚类的基础上引入了模糊理论，从而利用隶属度函数确定某一数据对象的划分类别。

FCM算法是一种基于目标函数的算法，把含有n个数据对象的集合X={x1,x2,…,xn}⊂Rs分为c类，其聚类中心用ci表示，目标函数是：

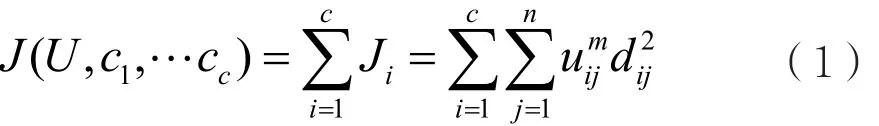
式中，uij取值在0到1之间，ci表示第i类的聚类中心，dij=||ci-xj||表示第i个聚类中心ci与第j个数据对象xj之间的欧几里德距离，而m∈[1,+∞)是加权指数，用来控制聚类的模糊程度。m值越大，表示模糊程度越大。

在约束条件的约束下，利用Lagrange数乘法求取式（1）的最小值，得到聚类中心和隶属度的迭代表达式如下：

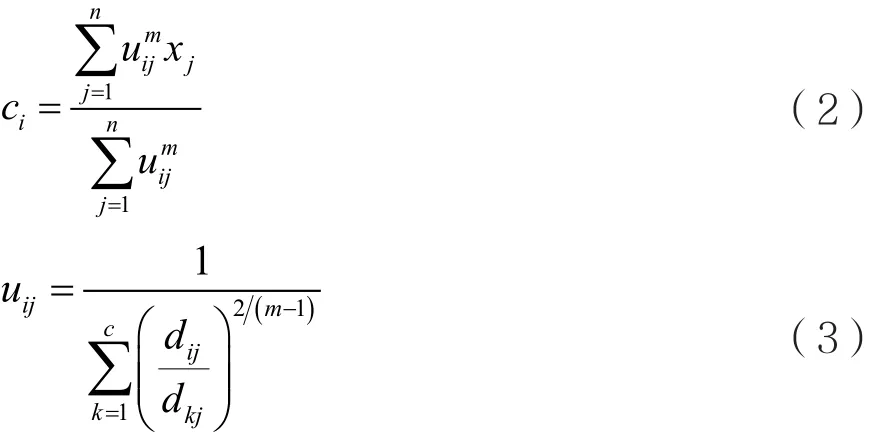
1.1.2 FCM算法的具体步骤

对FCM算法的具体实现步骤描述如下。

步骤1：初始化隶属度矩阵U，保证其值均在0到1之间，并使之符合约束条件；

步骤2：利用式（2）计算新的聚类中心ci,i=1,…,c；

步骤3：利用式（3）计算新的隶属度矩阵U；

步骤4：按照式（1）计算目标函数，如果它取得最小值或是超过最大的迭代次数，则算法结束，输出隶属度矩阵和聚类中心；反之，则返回到步骤2。

1.2 半监督模糊C均值聚类算法

1.2.1 SFCM算法的基本思想

SFCM算法把少量的labeled数据的类别标记当作监督信息，通过加入到FCM算法的目标函数，从而在整个聚类的迭代优化进程中起到一定的监督作用。另外，在隶属度方面也加入了带有半监督性质的表达式。此时，SFCM算法的目标函数为：

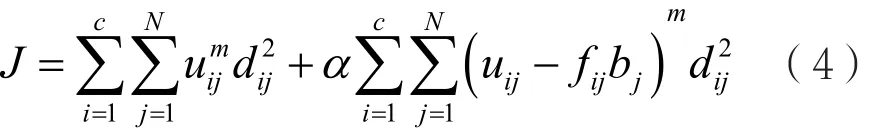
式中，m表示加权指数，是一个经验值，通常取值为2；α(α≥0)表示平衡因子，用来调节式（4）中的无监督信息与监督信息彼此间的平衡，其中α的具体值和总样本数L与标记样本数L的比值成正比例关系；fij为labeled样本的隶属度矩阵，其值具体表示为xj归于ci的程度大小；bj为一个布尔型的二值向量，按照它的实际取值可以用来判断xj是否是已经标记的数据。bj需要满足的条件如下：

同样地，用Lagrange数乘法对式（1）所表示的目标函数求解，最终获得的模糊隶属度uij和聚类中心vi的迭代表达式为：

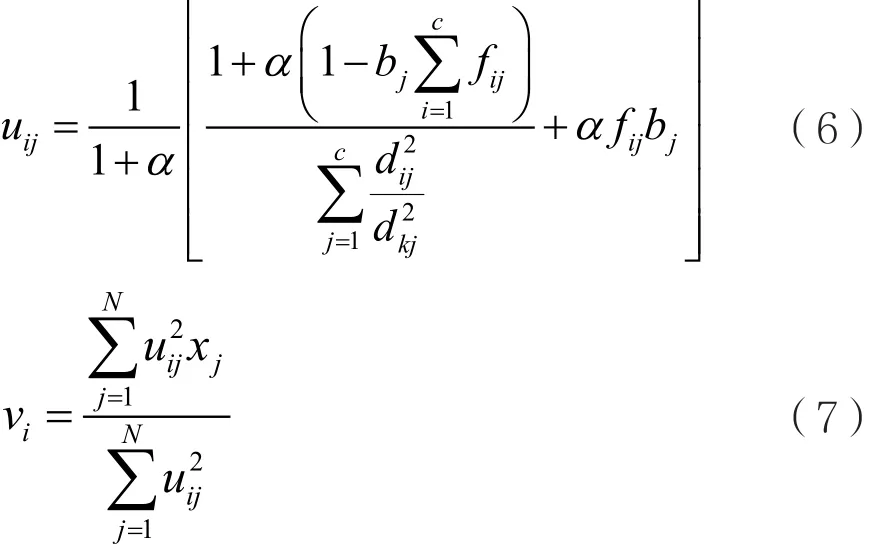
1.2.2 SFCM算法的具体步骤

输入：需要聚类的数据对象集合X，聚类的类别数c以及带有labeled信息的约束集S。

输出：聚类中心V，隶属度矩阵U。

（1）首先利用带有labeled信息的数据在集合S中进行初始划分，然后把得到的结果看作是算法的初始聚类中心；

（2）计算需要聚类的数据集合X和约束集S中所有样本点与聚类中心的距离，并按照式（5）生成初始隶属度矩阵；

（3）按照式（4）计算目标函数。假如它比预先给定的阈值小，又或者是前后两次的差小于阈值，那么算法结束；否则，转到步骤（4）；

（4）按照式（7）计算更新后的聚类中心，返回步骤（2）。

2 改进半监督模糊C均值聚类算法

2.1 SSFCM算法的基本思想

在SFCM算法中，随着监督信息的比重增大，算法的聚类性能指标也会更好。但在实际应用中，因为labeled数据难以大量获取，所以先验信息具有稀少性，即|XL|＜|XU|（|XL|代表labeled样本的数量，|XU|代表unlabeled样本的数量）。这将会导致SFCM算法的聚类性能降低，和FCM算法相比，体现不出本身的优越性。此时，labeled数据的类标记信息相对unlabeled数据来说已经很稀少，如果仍然仅仅依靠目标函数中的不可避免将忽略labeled数据的指导作用。

为了避免出现上述现象，参照文献[13]，采用把表示labeled数据点权重的参数放在聚类中心的迭代表达式的方法，以调节监督信息的影响力。具体做法是把表示SFCM算法聚类中心的迭代表达式更改为：

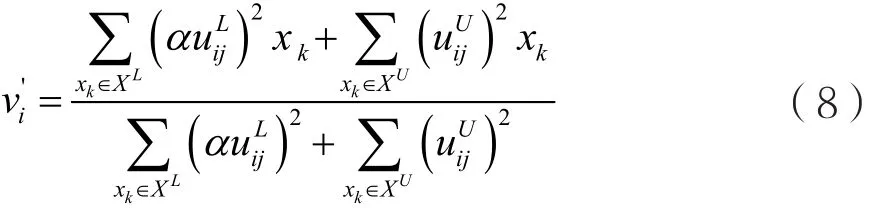
式（6）表示的是SFCM算法中的隶属度矩阵的迭代公式，因为标记信息的初始隶属度矩阵fij满足0≤fij≤1，且，把式（5）代入，则SFCM算法中的labeled数据和unlabeled数据的隶属度矩阵的迭代公式分别变为：

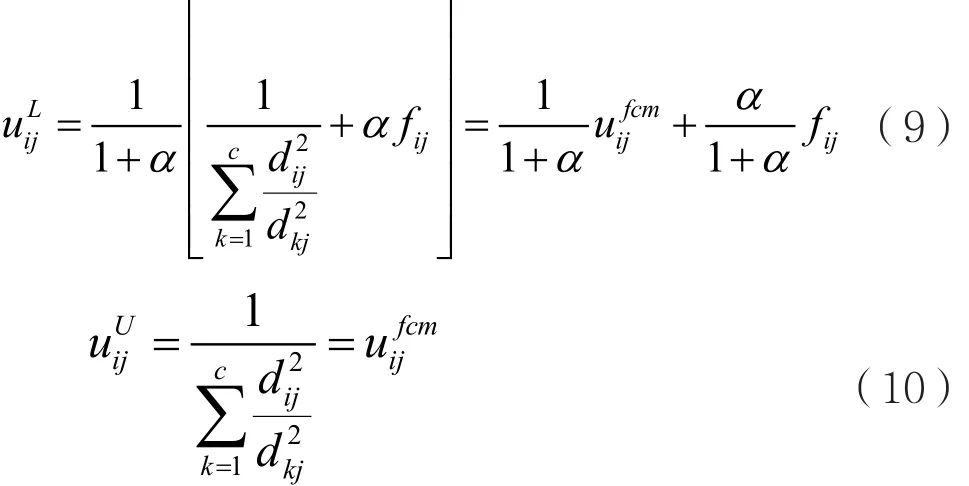
按照式（8），对聚类中心的迭代表达式式（7）进行修改，相当于保持SFCM算法的迭代方式，仍为原样。另外，对于隶属度矩阵的迭代表达式式（6），根据式（11）和式（12）对labeled数据和unlabeled数据的隶属度矩阵的权重做出对应形式的修改：

为了使改进算法的隶属度矩阵和聚类中心的迭代表达式与SFCM算法的表达式保持相似，对于式（12），这里采用1+α替换α。此时，相对应的式子将变成如下形式：

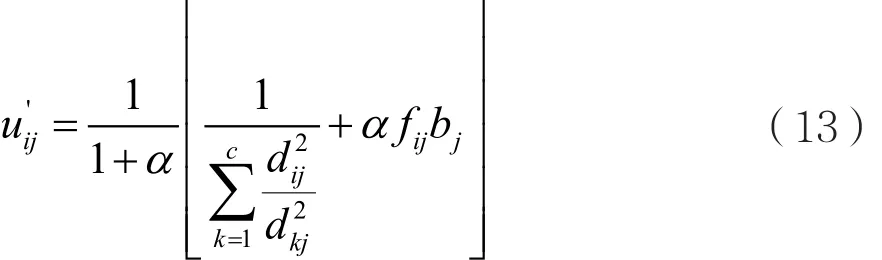
2.2 SSFCM算法的具体步骤

（1）初始化。设置聚类个数c，平衡指数α，由标记信息计算给出二值向量b=[ bj]和标记信息的初始隶属度矩阵F=[ fij]。

（2）计算labeled和unlabeled的所有样本点与聚类中心的距离；

（3）由式（13）计算新的隶属度矩阵U；

（4）由式（14）计算新的聚类中心V；

（5）本次计算得出的聚类中心与上次相比；不发生变化或者满足迭代次数超出最大次数，则算法停止；否则，返回步骤（2）。

3 实验验证

为了验证本文算法的合理性，选取美国加州大学欧文分校提出的UCI数据库中的Iris数据集，使用matlab编程验证及评估SSFCM算法的聚类性能。

为了便于对后面实验的聚类结果进行评价，这里引入一个指标RI=n0/n。对测试集进行实验后，把得到的分类结果与标准数据集本身分好的类进行对比，计算得到正确分类的数据条数即为n0，n则为测试集中数据的总条数。很明显，由表达式可知，RI表示的数值越大，聚类实验的准确性越高，即聚类性能越好。

实验过程中，分别使用FCM、SFCM和SSFCM算法进行测试比较。为了说明实验结果的可靠性，FCM、SFCM和SSFCM这3种算法在实验中均采用欧式距离。另外，SFCM和SSFCM算法的labeled样本点要选取相同的，数量均为10个，且labeled样本点的初始隶属度相同。分别利用3种算法依次对Iris数据集测试，每种算法都测试10次，最终的测试结果如表1所示。

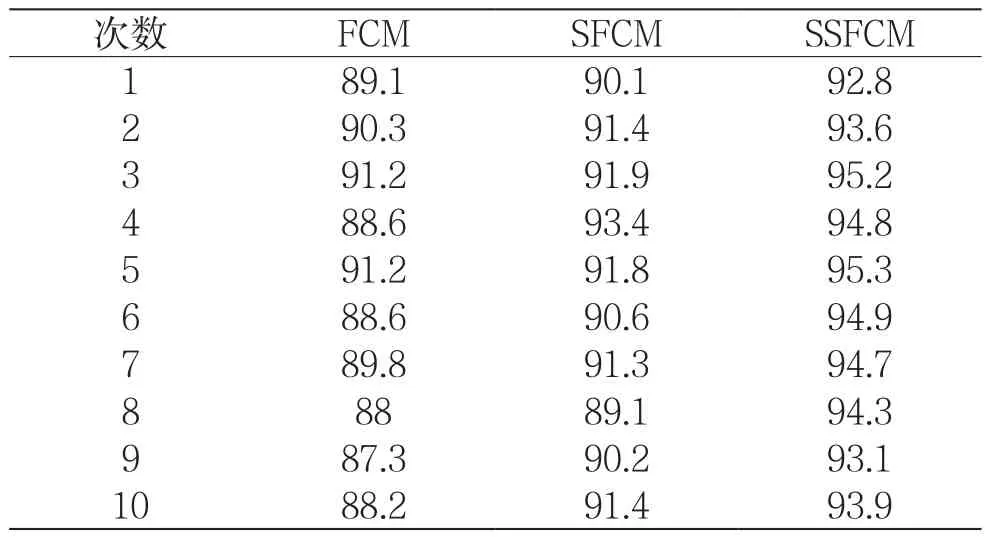
表1 FCM、SFCM、SSFCM算法准确率 /（%）

根据表1中10次测试获得的正确率，可以绘制如图1所示的对比结果，由其中的折线可以更直观地观察分析。

图1 FCM、SFCM及SSFCM算法对比

由图1的3条折线可以清楚看出，FCM算法、SFCM算法和SSFCM算法的准确率大小依次为：SSFCM算法最大，SFCM算法其次，最后是FCM算法，与理论分析结果一致。和FCM算法相比，SFCM算法充分利用了labeled数据的监督信息，而SSFCM算法在整个聚类的迭代进程中不断更新调整监督信息的比重，所以才会出现图1所示的情况。观察图中的折线可以清楚看到，FCM算法的准确率波动最大。算法中，除了初始聚类中心，剩下的所有参数都是固定不变的。所以，可以得到如下结论：在聚类算法中，初始聚类中心位置的选择将会对整个聚类结果的优劣起到很大作用。从图1中也可以看出，SSFCM算法的准确率和FCM、SFCM算法相对比更加平稳，数值上也高于FCM和SFCM算法。计算3种测试结果的平均值，得到如图2所示的柱形图。

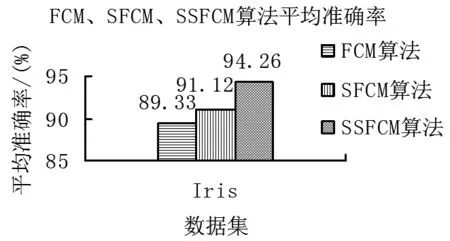
图2 FCM、SFCM及SSFCM算法平均准确率对比

表2从准确率、迭代次数和运行时间3个方面多角度对比显示了3种算法的聚类结果。从运行时间方面来说，SSFCM算法运行时间最少，仅仅用了0.065 s；FCM算法其次，用时0.188 s；最后是SFCM算法。从迭代次数方面来说，SSFCM、FCM和SFCM这3种算法的迭代次数依次增多，和算法的运行时间保持一致。从聚类准确度方面分析，SSFCM算法达到最大值，为94.26%；而FCM算法因为没有labeled样本做指导，聚类的准确率是3种算法中最小的，为89.33%；SFCM算法居中，为91.12%。综合来看，无论用3个方面的哪一个评价，SSFCM算法的聚类性能都要优于其他3种聚类算法。

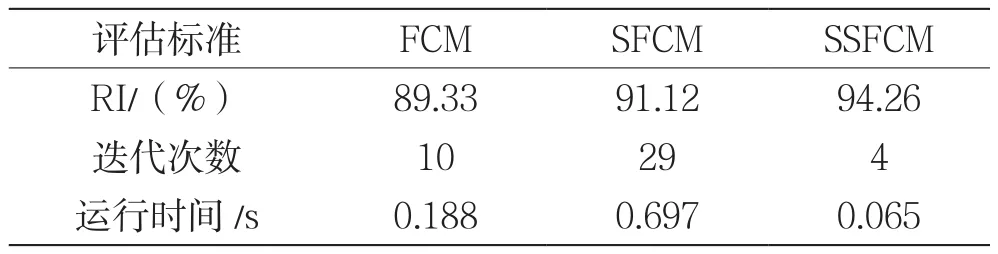
表2 FCM、SFCM及SSFCM算法聚类效果对比

4 结 语

半监督聚类中标签数据的获取需要一定的代价。所以，在实际应用的数据集中，标签数据的量都是比较少的，此时SFCM算法并不能很好地体现它的优势。因此，本文重新定义了SFCM算法的迭代公式，把表示labeled数据点权重的参数放在聚类中心的迭代表达式中，从而调节监督信息的影响力。其次，通过matlab编程对机器学习库中的Iris数据集进行了测试验证。最后，具体分析了该改进算法SSFCM的准确率，并与前面的基本算法进行实验对比，通过实验结果证明了该改进算法具有的良好性能。

参考文献：

[1] Wagstaff K,Cardie C,Rogers S,et al.Constrained K-means Clustering with Background Knowledge[C].Eighteenth International Conference on Machine Learning,2001：577-584.

[2] Huang H,Cheng Y,Zhao R.A Semi-supervised Clustering Algorithm Based on Must-Link Set[M].Advanced Data Mining and Applications. Springer Berlin Heidelberg,2008：492-499.

[3] Pedrycz W.Algorithms of Fuzzy Clustering with Partial Supervision[J].Pattern Recognition Letters,1985,3(01)：13-20.

[4] Li K,Cao Z,Cao L,et al.A Novel Semi-supervised Fuzzy C-means Clustering Method[C].Control and Decision Conference,2009：3761-3765.

[5] Blum A,Mitchell T.Combining Labeled and Unlabeled Data with Co-training[C].Eleventh Conference on Computational Learning Theory,2000：92-100.

[6] Wu L,Hoi S C H,Jin R,et al.Learning Bregman Distance Functions for Semi-Supervised Clustering[J].IEEE Transactions on Knowledge & Data Engineeri ng,2010,24(03)：478-491.

[7] Roy M,Ghosh S,Ghosh A.Change Detection in Remotely Sensed Images Using Semi-supervised Clustering Algorithms[J].International Journal of Knowledge Engineering & Soft Data Paradigms,2013,4(02)：118-137.

[8] 何振峰,熊范纶.结合限制的分隔模型及K-Means算法 [J].软件学报 ,2005,16(05)：799-809.HE Zhen-feng,XIONG Fan-lun.Limited Separation Model and K-Means Algorithm[J].Journal of Software,2005,16(05)：799-809.

[9] 肖宇,于剑.基于近邻传播算法的半监督聚类[J].软件学报 ,2008,19(11)：2803-2813.XIAO Yu,YU Jian.Semi-supervised Clustering Based on Nearest Neighbor Propagation Algorithm[J].Journal of Software,2008,19(11)：2803-2813.

[10] Chen M S,Wang S W.Fuzzy Clustering Analysis for Optimizing Fuzzy Membership Functions[J].Fuzzy Sets &Systems,1999,103(02)：239-254.

[11] 唐亮,黄培之,谢维信.顾及数据空间分布特性的模糊C均值聚类算法研究[J].武汉大学学报(信息科学版 ),2003,28(04)：476-479.TANG Liang,HUANG Pei-zhi,XIE Wei-xin.Study on Fuzzy C-means Clustering Algorithm Considering Spatial Distribution of Data[J].Engineering Journal of Wuhan University(Information Science Edition),2003,28(04)：476-479.

[12] Bezdek J,Hathaway R,Sobin M,et al.Convergence Theory for Fuzzy C-means：Counterexamples and Repairs[J].Systems Man & Cybernetics IEEE Transactions on,1987,7(05)：873-877.

[13] Bensaid A M,Hall L O,Bezdek J C,et al.Partially Supervised Clustering for Image Segmentation[J].Pattern Recognition,1996,29(05)：859-871.