关于反应位移法中地层变形模式的讨论

禹海涛

(1.同济大学岩土及地下工程教育部重点实验室,上海 200092; 2.上海市政工程设计研究总院(集团)有限公司,上海 200092;3.同济大学地下建筑与工程系,上海 200092;4.江苏博源土地规划设计咨询有限公司,南京 210004; 5.溧阳市水利局,常州 213300;6.驻马店市板桥水库管理局,驻马店 463715)

0 引 言

当前,我国城市地下空间的开发利用正在以前所未有的速度发展。以往人们普遍认为地下结构的数量较少,地下结构的抗震性能又优于地面结构,因此地下结构的抗震问题一直没有得到重视。直到1995年日本阪神大地震,地铁车站及区间隧道等不同类型的地下结构均遭受了严重破坏。自此,地下结构抗震问题日益受到世界各国地震工作者的高度重视。

早在20世纪初期,日本学者大森房吉最早提出静力理论指导隧道抗震设计,后续又有其他学者[1]提出了不同的计算理论,其中日本于20世纪70年代提出的反应位移法应用最为广泛。“汶川”地震之后,我国开始重视地下结构抗震问题,并相继出台了国家及地方新版设计规范,包括国家规范《城市轨道交通结构抗震设计规范》(GB 50909—2014)[2]和上海市地方规范《地下铁道建筑结构抗震设计规范》(DG/TJ 08-2064—2009)[3],两种规范均推荐反应位移法作为地下结构抗震设计方法。由于地下结构与土体动力相互作用的复杂性,目前规范对于关键参数如地层相对位移等仅做了笼统介绍,未能给出明确的计算公式。规范[2]中介绍的计算方法主要分为两种:基于波动理论的等效线性化方法和基于均质土假定的速度反应谱方法。鉴于地层相对变形为反应位移法的主要荷载来源,地层变形模式的确定对反应位移法的计算精度会产生较大影响,但其计算方法尚不统一。本文采用基于等效线性化理论SHAKE91程序,探究各类场地条件下地层的真实变形模式,并讨论速度反应谱方法用于计算地层相对位移的适用性。

1 反应位移法

反应位移法是20世纪70年代,日本学者从地震观测入手提出的地下结构抗震设计方法。其主要思想为:地下结构的地震动响应主要由其周围土层运动控制,把周围土体看作支撑结构的地基弹簧,将周围土体在地震作用下产生的位移通过地基弹簧以静荷载的形式施加给结构,分析结构的地震动响应[4]。反应位移法假定:①结构与土体均为各向同性的线弹性体;②忽略土体之间的相互影响[5]。

反应位移法把地震荷载主要分为三部分:土层的相对位移、地层剪力、结构自身惯性力,其计算模型如图1所示。研究表明,土层相对位移和地层剪力是影响结构响应的主要因素,结构自身惯性力的影响较小。关于地层位移的确定,目前主要使用两种方法:①利用一维土层地震反应分析程序(SHAKE91等)计算土层位移;②参考日本规范[6]的速度反应谱法。

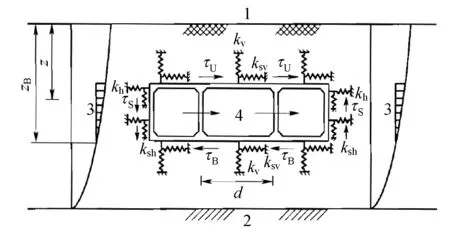
图1 反应位移法横断面计算模型[2]Fig.1 Simplified model for cross section calculation using Response Displacement Method[2]

2 地层变形计算理论

2.1 等效线性化方法

土体在动力荷载作用下,不但具有黏弹性特征,同时还表现出复杂的非线性。其动力非线性对场地动力响应影响较大,且动力荷载越大,非线性特征越显著,影响越大。目前工程界处理土体动力非线性主要采用等效线性化波动方法。等效线性化方法认为土体的非线性主要表现为:土体剪切模量随剪应变幅值增大而衰减,阻尼比随剪应变幅值增大而增大。

等效线性化方法中,土体在动力荷载下的剪切模量和阻尼比由等效剪应变幅值确定,而土体在确定动力荷载下的等效剪应变幅值受剪切模量和阻尼比的影响,故需采用迭代法确定等效剪应变幅值。具体方法为:先给定土体初始等效剪应变幅值,确定相应的剪切模量和阻尼比,完成土体动力分析,得到土层新的等效剪应变幅值,根据新的土层等效剪应变幅值确定相应的剪切模量和阻尼比,再进行土层动力分析,如此重复上述步骤,直到相邻两次计算得到的土层等效剪应变幅值相对误差满足精度要求为止[7]。

基于土层地震反应的等效线性化方法,学者们编写了一些进行一维土层地震反应分析的程序。目前国内常用的一维土层地震反应分析程序有SHAKE、EERA、PSLNLM等。本文分析采用SHAKE91程序。

SHAKE91程序是SHAKE程序系列的其中一个版本,SHAKE程序是由Per Schnabel博士和John Lysmer教授于1970年—1971年编写,随后成为了计算水平成层土体地震反应应用最为广泛的程序。随着一维等效线性化方法的不断发展,SHAKE程序逐步完善,推出了多个改进版本[8]。SHAKE91程序是功能较完善、目前较常用的版本。

SHAKE91程序采用基于Kelvin-Voigt模型的等效线性化模型描述一维土体的应力应变关系[9],即

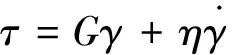
(1)

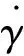
一维剪切梁简谐运动中,由位移、应变、应变率的关系,同时引入临界阻尼比ξ

τ=G*γ

(2)

式中：G*为复剪切模量(Pa),SHAKE91程序中假定G*为临界阻尼比ξ的函数:

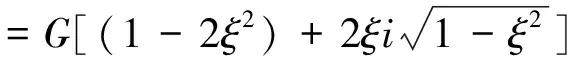
(3)

此前一些试验表明,等效线性化方法能够较真实地反映土体的地震动响应。齐文浩等[10]利用响瞠井下三维台阵的基岩实际强震记录对2种等效线性化程序(SHAKE91、LSSRLI-1)和1种真非线性程序(DENSOR98)进行了检验。检验结果表明,三种程序的计算结果与实际记录差异不大,可满足工程计算的精度要求。

2.2 速度反应谱法

利用速度反应谱计算地层位移的方法源自日本规范[6],该方法是在均质半无限体土层地震反应的解析法基础上得到的。

首先,建立均质半无限体(图2)的运动微分方程:

(4)

式中：γs为土的重度(N/m3);g为重力加速度(9.8 m/s2);u为地层位移(m);Cs为地层的黏滞衰减系数(N·s/m);Gs为地层剪切模量(Pa);uB为基岩位移(m)。

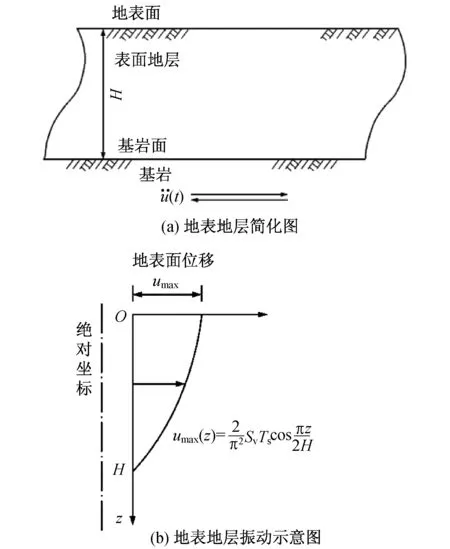
图2 地层地震位移响应[6]Fig.2 Deformation dynamic response of ground[6]

为了简便,假定土体剪切模量Gs不随深度的变化而变化,由此得到土层的自由振动方程为

(5)

由式(5)解得振型向量:

(6)

式中,ω为表层地层的固有频率(Hz);Vs为表层地层的剪切波速(m/s)。

采用振型叠加,体系的位移是由各振型向量乘以相应的组合系数后叠加而成的,则

(7)

式中：ui(z,t)为i次振型的地层位移(m);Xi(z)为i次振型的振型向量;qi(t)为i次振型的广义坐标,其可由如下微分方程求出:

(8)

式中：hi为i次振型的衰减系数;Γi为i次振型的振型参与系数。

通过Duhamel积分可得到由反应谱和振型参与系数表示的最大的振型向量[11]。利用式(7)进行振型组合,得地层最大位移:

(9)

式中:qimax为i次振型广义坐标的最大值。

通常只考虑一次振型,并引入位移反应谱和速度反应谱的换算关系,可得到地层深度z处最大位移的近似解:

(10)

式中:Sv为地层速度反应谱(m/s);Ts为地层的固有周期(s)。

3 不同场地条件的地层变形模式

反应位移法的计算精度主要由地层变形模式控制,正确的地层变形模式是反应位移法计算精度的保障。速度反应谱法表明均质土体的变形模式为正弦曲线形状。然而实际工程中的土层性质沿深度有所变化,使用该方法必然产生误差。等效线性化方法可用于分析分层土的地震动响应,且精度较高。本文采用基于等效线性化理论的SHAKE91程序,分析不同场地条件的地层变形模式,并评价速度反应谱法的适用性。

3.1 场地条件

《城市轨道交通结构抗震设计规范》(GB 50909—2014)[2]按照土层剪切波速和覆盖层厚度把场地分为Ⅰ类到Ⅳ类,不同类别场地表现出不同的地震动响应特性。本文选取了Ⅰ类场地(青岛地层)、Ⅱ类场地(厦门地层)、Ⅲ类场地(南京地层)、Ⅳ类场地(上海地层)4类典型的场地,利用SHAKE91计算土层位移。本文的工程背景为:一个顶板埋深1.7 m、高13.76 m的两层三跨地铁车站,主要探究结构所在处的土层相对位移模式。限于篇幅,这里仅给出结构所在处4类场地的地层参数,如表1所示。

为考虑土体的动力非线性特征,基于等效线性化理论的SHAKE91程序进行一维土层地震反应分析时,需要土体的动力特性曲线,即土的G/Gmax、阻尼比与剪应变的关系曲线。本文给出了结构所在处主要土层的动力特性曲线,如图3所示。

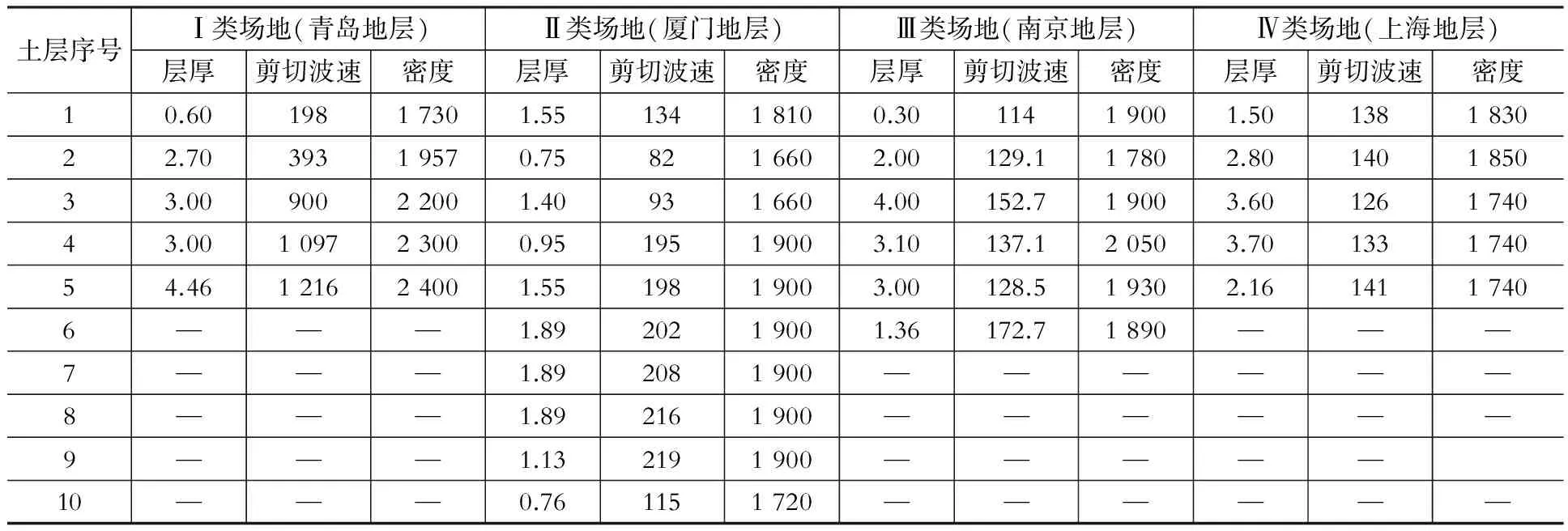
表1 结构所在处不同场地类别的地层参数Table 1 Ground parameters of differentsite classifications around the structure

3.2 计算参数及工况

等效线性化方法关键参数为土体剪切模量和阻尼比随剪应变幅值变化的关系曲线,本例中每层土都选取了相应的关系曲线。土层按照天然土层划分,地震波输入面统一选取地表以下70 m处。

鉴于土的非线性特征受地震动强度的影响,输入地震动选取三种不同强度的地震波。按照《城市轨道交通结构抗震设计规范》(GB 50909—2014)[2]抗震设防要求,本文选取了地震动水平等级分别为E1、E2、E3的三种同类人工波。限于篇幅,这里仅给出E2地震波的加速度时程曲线,如图4所示。

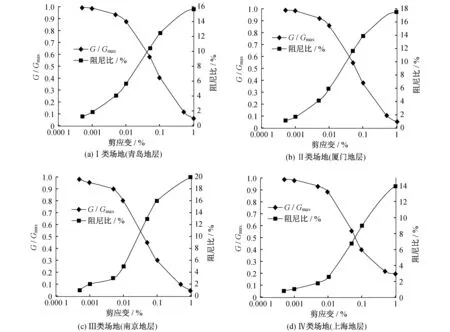
图3 土的动力特性曲线Fig.3 Dynamic characteristic curve of soil

图4 地震波加速度时程曲线(E2)Fig.4 Acceleration time-history cure of seismic wave(E2)

3.3 对比分析

现以SHAKE91的计算结果为基准,评价速度反应谱法的适用性。关于我国场地速度反应谱的资料相对缺乏,为保证两种方法的地震动水平一致,可把式(10)中的SvTs看作一个整体未知量,由SHAKE91的计算结果求解该未知量。具体方法为:

(11)

(12)

联立式(11)、式(12)可求得:

(13)

式中:z(1)为结构顶板埋深(m);z(2)为底板埋深(m);u[z(1)]为顶板处SHAKE91所得位移(m);u[z(2)]为底板处SHAKE91所得位移(m);H地震波输入面到地表的距离 (m)。由式(13)计算每种地震动作用下土层的SvTs值,即可采用式(10)计算土层各深度的位移。

由图5所示的结果可知,随地震动水平等级的提高,土层位移随之增大;且同种地震动水平下,土层位移随其剪切波速的增大而减小。同时,由于不同场地的地层分布不同,故由SHAKE91分析得到的地层变形模式有所差异。

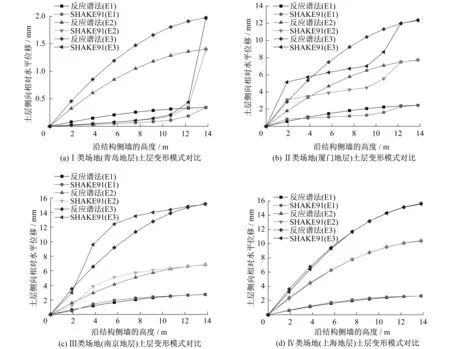
图5 计算结果对比Fig.5 Results comparison between two methods

结合各类场地的地层参数(表1),分析两种不同分析方法得到的土体变形模式的差异性。Ⅳ类场地中,各层剪切波速基本一致,均匀性较好,速度反应谱法得到的土层位移曲线与SHAKE91基本完全重合,都表现为标准的正弦曲线性状。由此证明:对于均质地层,速度反应谱法通过求解均质半无限土体的运动微分方程,仅考虑一次振型的计算结果是合理的。

Ⅲ类场地中,结构侧墙中下部所在深度处,地层存在一个剪切波速较小的软弱夹层,地震动作用下夹层处的剪应变较大,从而造成相对位移较大,因此速度反应谱法计算得到的位移曲线在软弱夹层所在处较SHAKE91明显偏小。

Ⅱ类场地中,地层参数表现出顶底部软而中部硬的特征,中部坚硬土层变形较小,土体变形集中发生在顶部和底部;Ⅰ类场地中,地层参数表现出明显的上软下硬特征,土体变形集中发生在上部;因此,对于地层分层差异性较大的场地,速度反应谱法得到的位移曲线与SHAKE91整体差距较大。

总体上,基于均质土层得到的速度反应谱法在剪切波速没有突变的均质地层可以准确地描述地层的变形模式,但当地层分层差异性大且剪切波速有较大变化,特别是存在软弱夹层时,地层的变形模式不再是正弦曲线形状,此时速度反应谱法适用性较差,且相邻土层的剪切波速差距越大,地震动水平等级越高,速度反应谱法得到的变形曲线与真实变形曲线相差越大。

4 结 语

采用均质土层近似代替分层土,便于分析计算,故速度反应谱法这类基于均质土推导的公式得到了广泛应用。但当地层剪切波速沿深度发生较大变化时,速度反应谱法将不再适用。为获得土体的真实地震动响应,必须分析非均质天然地层的地震动响应,等效线性化波动理论的出现为此提供了方法。等效线性化方法作为目前工程界处理土体动力非线性的主要方法,解决了众多地下结构的抗震设计问题。但目前对土体动力非线性特性的本质认识尚不深刻,等效线性化方法在工程使用中存在一定局限性,有待进一步发展。

参考文献

[1] 马建,孙守增,赵文义,等.中国隧道工程学术研究综述-2015 [J].中国公路学报,2015,28(14105):1-65.

Ma Jian,Sun Shouzeng,Zhao Wenyi,et al.Review on China’s tunnel engineering research:2005[J].China Journal of Highway and Transport,2015,28(14105):1-65.(in Chinese)

[2] 中华人民共和国国家标准编写组.GB 50909—2014城市轨道交通结构抗震设计规范 [S].北京:中国建筑工业出版社,2014.

The National Standards Compilation Group of People’s Republic of China.GB 50909—2014 Code for seismic design of urban rail transit structures [S].Beijing:China Architecture and Building Press,2014.(in Chinese)

[3] 中华人民共和国国家标准编写组.DG/TJ08—2009 地下铁道建筑结构抗震设计规范[S].上海:[s.n.],2009.

The professional standards compilation group of People’ Republic of China.DG/TJ08—2009 Code for seismic design of subway structures[S].Shanghai:[s.n.],2009.(in Chinese)

[4] 袁勇,禹海涛,陈之毅.软土浅埋框架结构抗震计算方法评价[J].振动与冲击,2009,28(8):50-56.

Yuan Yong,Yu Haitao,Chen Zhiyi.Evaluation of seismic calculation methods for shallow-buried frame structures in soft soil[J].Journal of Vibration and Shock,2009,28(8):50-56.(in Chinese)

[5] 禹海涛,袁勇,张中杰,等.反应位移法在复杂地下结构抗震中的应用[J].地下空间与工程学报,2011,7(5205):857-862.

Yu Haitao,Yuan Yong,Zhang Zhongjie,et al.Application of response displacement method on seismic design of a complex underground structure[J].Chinese Journal of Underground Space and Engineering,2011,7(5205):857-862.(in Chinese)

[6] 川岛一彦.地下构筑物の耐震设计[M].日本:鹿岛出版会,1994.

Kawajima K.Aseismic design of underground structure[M].Japan:Kajima Institute Publishing Co.,Ltd.1994.(in Japanese)

[7] 陈国兴.岩土地震工程学[M].北京:科学出版社,2007.

Chen Guoxing.Geotechnical earthquake engineering[M].Beijing:Science Press,2007.(in Chinese)

[8] Idriss I M,Sun J.User’s manual for SHAKE91 A computer program for conducting equivalent linear seismic response analyses of horizontally layered soil deposits center for geotechnical modeling[R] .Department of Civil & Environmental Engineering,University of California,Davis,California,August 1992.

[9] 齐文浩.土层地震反应分析方法的比较研究[D].北京:中国地震局工程力学研究所,2004.

Qi Wenhao.Study on the comparison of soil layers seismic response analysis methods[D] .Beijing:Institute of Engineering Mechanics,China Earthquake Administration,2004.(in Chinese)

[10] 齐文浩,薄景山,刘德东,等.强震记录对三个土层地震反应分析程序的检验[J].地震工程与工程振动,2005,05:32-35.

Qi Wenhao,Bo Jingshan,Liu Dedong,et al.A test for three programs of soil layer seismic response analysis by strong earthquake record[J].Earthquake Engineering and Engineering Vibration,2005,05:32-35.(in Chinese)

[11] 耿萍,张景,何川,等.隧道横断面反应位移法基本原理及其应用[J].岩石力学与工程学报,2013,32(277S2):3478-3485.

Geng Ping,Zhang Jing,He Chuan,et al.Basic theory of seismic deformation method in cross section of tunnel and its application[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(277S2):3478-3485.(in Chinese)