不确定磁悬浮轴承模型的自适应PID控制研究

李 莹，王西伟，谢 翔，顾冬梅，董长海

(安徽理工大学电气与信息工程学院，安徽 淮南 232001)

磁悬浮系统(Magnetic Levitation System，MLS)是利用电磁力对物体悬浮、旋转或移动，是一种非接触式操作方式，可有效地减少机械振动、摩擦和接触操作所造成的摩擦损失。还可以延长设备的使用寿命，减少维护频率和噪音[1]。随着控制技术领域的发展，诸多复杂多样的控制策略应用到磁悬浮，如早期的比列-积分-微分控制(Proportion Integral Derivative，PID)[2-3]、模糊滑模控制[4]、模糊神经网络[5-6]以及线性二次型最优控制[7]等，但磁悬浮系统本身就是一类典型的参数不确定性和非线性系统[8]，对系统的动态及静态性能要求很高，为磁悬浮控制系统的设计带来了挑战。

常规PID控制器简单、稳定，参数容易调整以及无静态误差，但当控制对象是时变系统时，控制器参数难以自动调整以适应外部环境的变化，模糊滑模控制由于主要依靠滑模面而与对象参数及扰动无关，但同时也因为高频率的切换产生严重的抖动现象。模糊控制不依赖于具体的数学模型，非线性系统控制的动态性能较好，但稳态性能较差。神经网络自学习适应复杂问题的能力和径向基函数(Radial Basis Function，RBF)神经网络[9]具有更快的学习速度和良好的泛化能力，能以任意精度逼近非线性系统，但当数据不充分的时候，神经网络就无法工作。

本文研究了RBF神经网络前馈逆补偿——模糊RBF神经网络反馈控制方法。将模糊控制和RBF神经网络融合到PID控制器参数调整中，一方面加快系统响应速度，另一方面由于神经网络特有逼近特性，使参数的调整更准确，从而提高对磁悬浮系统的控制效果。

1 磁悬浮轴承系统动力学模型

磁悬浮系统原理图如图1所示。其中m是钢球质量，x是电磁铁与钢球之间的距离，i是线圈绕组的电流，Fm(x，i)线圈通电时刚体的电磁力，Fd(t)是系统所受干扰力。在磁悬浮系统中，钢球悬浮在受电流控制的磁场中，通过控制电流将钢球悬浮在平衡位置，可建立一个基于电磁、电力和力学的磁悬浮系统数学模型。

图1 磁悬浮系统工作原理示意图

把钢球看作质子，根据牛顿第二定律，磁悬浮系统动力学模型为

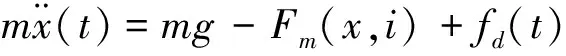
(1)

假设该系统具有理想的电磁特性，根据磁路理论可以得到电磁力[10-11]

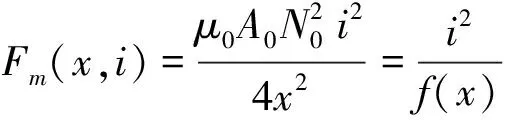
(2)

式中：μ0是空气磁导率，A0是磁极面积，N是电磁线圈的匝数，f(x)是悬浮距离x的多项式函数，可以表示为

f(x)=b0+b1x+b2x2+b3x3+b4

(3)

通过实验拟合，计算得出多项式(3)中的可用系数为：b0为-32.6，b1为4 897.3，b2为-274 970，b3为6 816 800，b4为-62 498 000。

由电磁感应定律可得到电磁电路电压

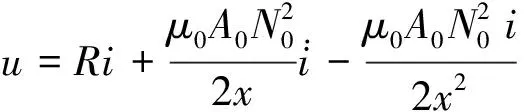
(4)

单自由度磁悬浮非线性系统模型由式(1)～(4)联立方程组成。

2 RBF前馈自适应模糊RBF反馈控制

2.1 系统结构

由于神经网络具有万能逼近能力，本文采用RBF网络建立磁悬浮系统的动态逆模型，消除其耦合影响。另一方面由于系统的建模以及神经网络逼近会产生一定的误差，为提高控制精度，在设计磁悬浮系统控制器时加入反馈控制。结合模糊控制、RBF神经网络各自的优点，将其融合到PID控制参数调整。系统控制结构如图2所示。

图2 基于模糊RBF网络的PID控制系统结构

总控制器u为

u=uRBF+uSML

(5)

式中：uRBF为RBF网络逆控制器的输出；uPID为PID控制器的输出。

2.2 模糊RBF网络PID控制

模糊RBF神经网络如图3所示，由输入层、模糊化层、模糊推理层、和输出层组成[12-13]。网络的输出是PID的参数Kp、KI、KD。

图3 模糊RBF神经网络结构

根据不同的功能将模糊RBF神经网络分为四层：

第一层 输入层，将系统误差及系统输出反馈结果作为输入层的两个节点，即x1=e，x2=yout[14-15]。对该层的每个节点i的输入输出表示为

f1(i)=X=[x1，x2，…，xn]

(6)

第二层 模糊化层，该层针对两个输入量总共设计6个模糊化集，由输入层可知本层输入为x1=e，x2=yout，本层输出为

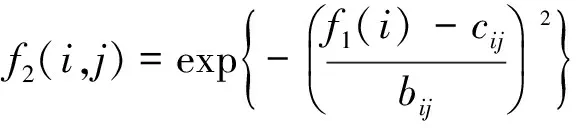
(7)

式中：cij和bij分别是第i个输入变量第j个模糊集合的隶属函数的均值和标准差。

第三层 模糊推理层[16]，该层为推理层，即设计6条模糊规则，由输入量对应的模糊集两两结合成一条模糊规则，由此得出点火强度。每个节点j的输出为该节点所有输入信号的乘积，即

(8)

第四层：输出层，将第三层的输出和连接权矩阵以矩阵乘的方式得出结果，因此，该层的输出为

(9)

式中：wij为输出层节点与第三层各节点的连接权矩阵。

通过上述分析可以得到控制器

kpxc(1)+kixc(2)+kdxc(3)

(10)

(11)

(12)

采用增量PID控制算法，得出u(k)表示为

u(k)=u(k-1)+Δu(k)

(13)

设计中，采用Delta学习规则修改可调参数。学习目标函数定义为

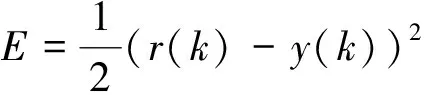
(14)

式中：r(k)和y(k)分别为实际网络输出和期望输出，网络逼近误差为

e(k)=r(k)-y(k)

(15)

利用梯度下降法对Kp、KI、KD进行参数调整。

(16)

(17)

(18)

输出层的权值通过如下方式来调整

(19)

式中：wj是输出层节点与第三层节点的连接权值，j=1，2，…，N，η为学习速率，η∈[0，1]。

加入动量因子，则输出层的权值学习算法为

wj(k)=wj(k-1)+Δwj(k)+α(wj(k-1)-wj(k-2))

(20)

式中：α为动量因子，α∈[0，1]。

3 仿真与分析

根据上述思想和规则，在simulink环境下设计一种RBF神经网络前馈逆补偿——模糊RBF神经网络反馈控制系统。取采样周期T=1s，利用临界比法选择三个PID参数：Kp=110，Ki=60，Kd=0.8。模糊RBF神经网络结构选择2-8-1，学习效率η=0.3，动量因子α=0.02。磁悬浮系统平衡值设置为2mm。

图4是常规PID和RBF神经网络前馈逆补偿——模糊RBF神经网络反馈的磁悬浮控制系统的响应曲线对比图，实线为模糊RBF神经网络控制响应曲线，虚线为常规PID控制曲线，有大约4%的超调，响应时间为0.3s。

图4 磁悬浮系统阶跃响应曲线图

为了验证系统的抗干扰能力，加入响应周期T=1.0s，振幅0.5mm 的干扰脉冲宽度，图5是系统脉冲扰动的响应曲线图，其中实线是PID控制响应曲线，虚线为模糊RBF神经网络PID控制整定曲线。

图5 干扰情况下磁悬浮系统响应曲线图

4 结论

仿真结果表明该网络可以获得比常规PID更快地响应速度，更优良的控制性能，适应能力强，抗干扰性能好，是一种值得推广的针对非线性系统的控制方案。

参考文献：

[1] JING ZHANG. Hamiltonian modeling and passive control of magnetic levitation system[J].Electric Machines and Control, 2008,12(4):464-467.

[2] 王晓乐，付小利，崔宸昱，等.基于多类别满意优化控制的磁悬浮球控制系统[J].仪器仪表学报，2015，36(9)： 1 928-1 936.

[3] 李社蕾，李海涛，王喜鸿.磁悬浮PID参数整定仿真[J].计算机仿真，2012，29(9)： 348-352.

[4] 刘春芳，胡雨薇.单电磁悬浮系统的神经网络模糊滑模控制[J].沈阳工业大学学报，2016，38(1)： 1-6.

[5] ZHENGGUO XU. Fuzzy logic based control strategy for hybrid-magnets used in maglev systems[J].Transactions of China Electrotechnical Society, 2006,21(10):76-80．

[6] SHAMELI, EHSAN. Nonlinear controller design for a magnetic levitation device[J]. Microsystem Technologies, 2007,13(5):831-835．

[7] 施佳余，吴国庆，茅靖峰，等.磁悬浮轴承系统控制方法研究[J].机械设计与制造，2015(12)： 265-268.

[8] 张静，方燕.磁悬浮系统的积分变结构控制[J].哈尔滨理工大学学报，2009，3(14)：9-12.

[9] 赵石铁，高宪文，车昌杰.基于RBF神经网络的非线性磁悬浮系统控制[J].东北大学学报，2014，35(12)：1 673-1 676.

[10] SYUAN YI CHEN，FAA JENG LIN. Direct decentralized neural control for nonlinear MIMO magnetic levitation system[J].Neurocomputing,2009,72(2):3 220-3 230．

[11] 张静，裴雪红，邢海峰，等.磁悬浮改进RBF神经网络控制的仿真研究[J].哈尔滨理工大学学报，2011，16(1)： 48-52.

[12] 吴勇，王超.基于RBF网络辨识的航空发动机模糊神经网络解耦控制[J].燃气涡轮试验与研究，2010，23(2)： 15-18.

[13] 宋献峰，张克辉.基于模糊RBF神经网络的板带横向厚度和纵向厚度综合控制[J].金属铸锻焊技术，2012，41(13)： 132-137.

[14] SHEKHAR YADAV, J P TIWARI, S K NAGAR. Digital Control of Magnetic Levitation System using Fuzzy Logic Controller[J]. International Journal of Computer Applications, 2012,41(21):22-26.

[15] SHIEH, HSIN JANG. A robust optimal sliding-mode control approach for magnetic levitation systems[J]. Asian Journal of Control,2010,12(4):480-487.

[16] 谢克明，侯宏仑，谢刚，等.过热汽温系统的自适应梯阶模糊PID参数控制[J].中国电机工程学报，2001，21(9)： 38-42.