电动汽车电池SOC的估计
2018-05-24王建南荀锦锦
王建南,张 奎,荀锦锦
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
电池SOC的估算是电池管理系统(Battery Management System,BMS)的核心,也是当前研究的热点和难点。准确估算电池的SOC不仅是有效利用电池的先决条件,而且可延长电池的使用寿命,避免电池过充电和过放电,降低了对动力电池性能的要求。另外,SOC也是其他决策的输入变量。SOC的精确估算将会受到温度、充放电倍率、电池自放电以及电池寿命等因素的影响[1]。
对于电池SOC的估算算法,国内外的一些学者展开一些深入的研究,提出了许多经典的 SOC 估算方法,比如安时积分法、开路电压法、神经网络法和卡尔曼滤波法。文献[1]采用的是安时积分法估算电池的SOC,安时积分法对各种类型的电池都适用,算法简单稳定可靠,也是最常用的一种算法,由于算法的开环性质和采样精度的限制,导致累积误差较大,实际的应用中,一定的误差范围内都会认为是准确的;文献[2]采用的是卡尔曼滤波算法估算电池SOC,卡尔曼滤波算法是一种闭环递归方法,可有效解决SOC初始估计误差以及误差积累的问题,但仅适用于线性系统;文献[3]采用扩展卡尔曼(EKF)算法,EKF算法是针对非线性系统应用的一种最普遍的状态估计方法,通过泰勒公式对非线性系统进行线性化,忽略高阶项,引入线性化误差,比较适合电池SOC的估算;文献[4]采用AEKF 算法估计电池 SOC,用一种改进的参数辨识方法获得模型参数,提高了电池SOC的估算精度。本文采用无迹卡尔曼(UKF)估算电池SOC,UKF算法是卡尔曼滤波的延伸,可降低EKF线性化带来的误差,所以UKF算法更适合电池SOC的估算。
进行电池SOC估算之前,必须建立一个准确的电池模型,然后获取电池模型参数[5],模型参数通常在线变化。采用最小二乘法辨识数据时误差较大,导致电池SOC估计不准确;递推最小二乘法是在计算控制的前提下辨识电池模型参数,提高参数的校正能力,使模型参数快速收敛到模型参数的真实值。因此采用递推最小二乘法进行电池模型的参数识别[6]。
本文通过UKF算法对电池SOC进行估算[7],探索该算法是否能准确估计电池SOC。建立合适的电池模型,通过递推最小二乘法在线识别模型参数。在此基础上,完成对电池SOC的估算,与理想状态下的SOC进行比较,验证该算法对电池SOC估算的精准度。
1 锂离子电池模型
等效电路模型包括线性模型、Thevenin模型、PNGV模型等。考虑到电池模型的精确度以及复杂性等特点,选择二阶RC等效电路模型来估计电池SOC,该模型结构简单,计算量适中,便于参数辨识,工程上也容易实现[8],模型如图1所示。

图1 电池的二阶RC等效电路
其中:Uoc是电池开路电压,R是电池欧姆内阻,R1和C1是极化电阻和电容,R2和C2是浓差电阻和电容。该模型用于模拟端电流It与端电压Ut之间缓慢变化的关系,时间常数τ1=R1C1较小,τ2=R2C2较大,U1、U2分别为R1、R2的端电压,根据基尔霍夫定律和电路的动态特性可以得出
(1)
电动势Uoc和电池SOC的关系如图2所示。

SOC图2 锂电池的开路电压与SOC的关系
通过式(1)获得端电压
Ut(t)=Uoc(SOC)-It(t)R0-
(2)
2 模型参数识别
二阶RC等效电路模型参数R、R1、R2、C1、C2等需通过在线辨识。模型的参数随着电池工作的进行而不断变化,通过离线辨识得到的电池模型参数往往不够准确,还要进行实时的修正才能反映当前电池的性能。本文采用递推最小二乘法法对电池模型参数进行在线识别[9]。根据拉普拉斯变换可得到在S域中有
(3)
式中:U(t)=Uoc(t)-U(t),U(s)和I(s)分别是U(t)和It(t)的拉氏变换[6]。
定义:
(4)
通过公式(3)可以得到如下公式
(1+a1s2+a2s)U(s)=(a3+a4s+a5s2)I(s)
(5)
定义:

(6)
式(5)可以变为如下差分方程
U(k)=b1U(k-1)+b2U(k-2)+b3I(k)+
b4I(k-1)+b5I(k-2)
(7)
b1~b5可通过以下公式获得
(8)
式中:Δt是采样间隔时间。
定义:
(9)
式(7)可变换成:U(k)=HT(k)θ
(10)
(11)

3 UKF算法估算电池SOC
3.1 建立状态方程和观测方程的电池模型
从电池SOC理论测量方法得出AH法估算SOC[11]

(12)
式中:SOC(t)是电池荷电状态,SOC(t0)是初始SOC的状态,Qe是电池额定容量,i是放电电流t0到t的瞬时值。η是充放电效率,它与充放电电流、电池温度以及电池寿命有关[12]。
通过式(12)和式(1)得到以下递归公式

(13)
U1(k)=Uoc(SOC(k))-U1(k)-U2(k)-
R0I(k)+v(k)
(14)
其中:式(13)被称为状态方程组,w(k)是过程噪声;式(14)被称为系统的观测方程,v(k)是测量噪声。
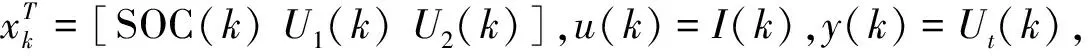
(15)
3.2 UKF算法与实现
UKF算法的关键是无迹变换,无迹变换最大的优势是均值和协方差变换过程中有更高的精确度[13]。
无迹变换以两条准则为基础:1)对单一点执行非线性变换是容易的;2)状态空间中不难找到一组点,利用这些点可近似状态向量的真实概率分布函数。在此基础上,假设已知向量x的均值和协方差,找到一组确定的向量称作sigma点,且sigma点的均值和协方差与x相同。然后将每一个向量经非线性函数y=h(x)进行无迹变换,得到变换后的向量,变换后向量的均值和协方差将准确地估计出y的真实均值和协方差。
假设过程噪声和测量噪声是不相关的高斯白噪声,其统计特性如下
wk~N(0,Qk),vk~N(0,Rk)
1)无迹卡尔曼滤波初始化如下
(16)
2)状态估计
计算Sigma点[14]
(17)

时间过程方程

(18)
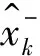
测量时间方程
(19)
3)确定加权系数和比例参数

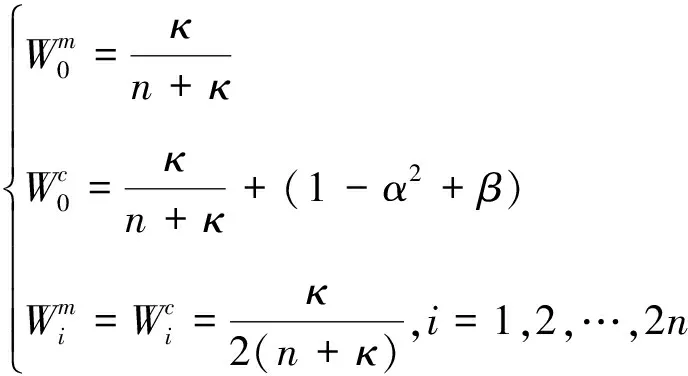
(20)
式中:系统参数κ=α2(n+λ)-n。
计算均值和协方差的加权系数需要确定参数α/λ和β。使用sigma点近似状态变量x的分布,α在较小范围内(e-4≤α<1),λ通常取0;β是状态分布参数,假设状态变量服从高斯分布,则β=2。
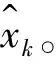
4 仿真与分析
本文选用的能量电池为磷酸铁锂电池,额定容量为11ah,额定电压为3.2V,最大充电电流为4c,最大放电电流为6c。充电截止电压为3.65V,放电截止电压为2V。实验结果表明,本文中温度的影响可以忽略不计。

4.1 仿真模型参数
电池的放电条件复杂且可变,为了模拟实际放电条件下模型参数的变化,本文跟踪了模型参数变化(见图3)。

(a)电池内阻辨识曲线

(b)电池电容辨识曲线图3 模型参数识别曲线
从图3可知,模型参数在放电过程中存在一定范围内的波动,具有一定的时变特性,与等效电路模型参数的实际情况相符。
4.2 UKF算法验证
仿真中,理想情况下采用AH法没有引起的累积误差或电压、电流等采集精度问题,所以AH法估计的SOC很接近电池SOC的真实值。图4是当电池处于恒流放电和可变电流放电情况下SOC模拟曲线。
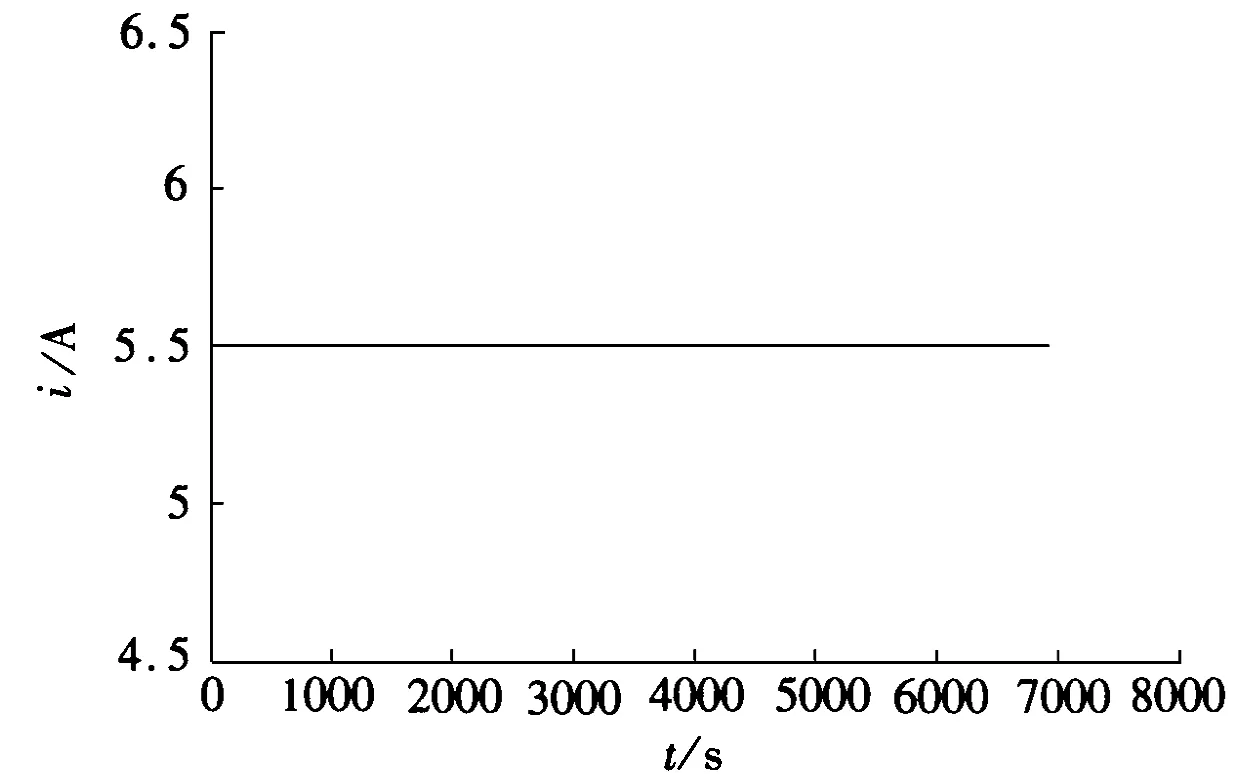
(a)恒定放电电流波形

(b)恒定放电电流下AH和UKF的SOC估计值
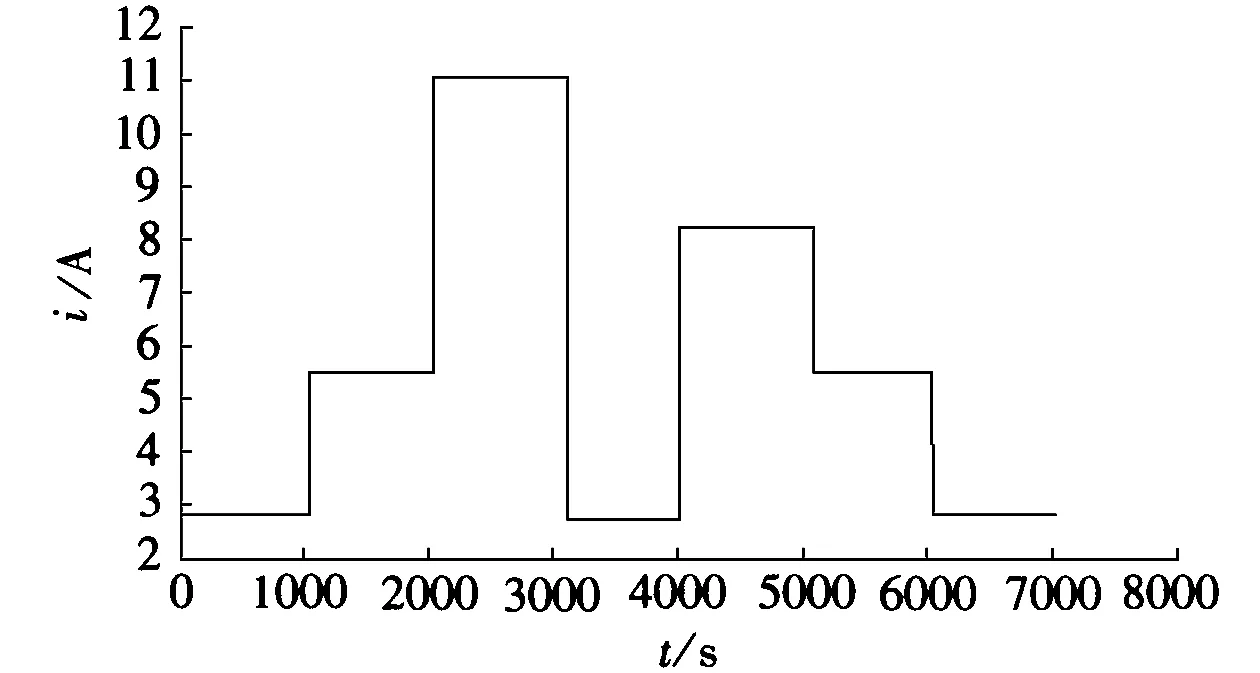
(c)脉冲放电电流波形

(d)脉冲放电电流下AH和UKF的SOC估计值图4 UKF和AH法估计SOC的仿真结果
由图4可知,当电池恒流放电时,电池SOC的变化几乎是线性的。UKF算法曲线和AH法曲线的变化大致相同,误差可以控制在3%左右;当可变电流放电时,UKF算法曲线和AH法曲线的变化趋势仍然很接近,整体误差稍大,可控制在5%左右。无论是恒流放电还是可变电流放电,UKF算法仿真曲线都很接近AH法仿真曲线,随着SOC的减少,误差变得越来越小,表明UKF算法对电池SOC估计很接近真实SOC值。
5 结论
由于电池SOC的估算受到环境温度、充放电倍率等因素的影响,使得SOC的估算不是很准确。本文在动态模型参数的基础上,采用UKF算法估算电池SOC,仿真结果表明,该方法对于电池SOC的估算具有一定的鲁棒性和较高的精度。
参考文献:
[1] 邓涛,孙欢.锂离子电池新型SOC安时积分实时估算方法[J].重庆理工大学学报(自然科学),2015,16(1):101-106.
[2] DAI H,WEI X,SUN Z,et al.Online cell SOC estimation of Li-ion battery packs using a dual time scale Kalman filtering for EV applications [J].Applied Energy,2012,95(2):227-237.
[3] 刘浩.基于EKF的电动汽车用锂离子电池SOC估算方法研究[D].北京:北京交通大学,2012.
[4] XIONG R,HE H,SUN F,et al.Evaluation on State of Charge Estimation of Batteries With Adaptive Extended Kalman Filter by experiment approach[J].IEEE Transactions on Vehicular Technolog,2013,62(1):108-117.
[5] 李超.电动汽车用镍氢电池模型参数辨识和 SOC估算研究[D].天津:天津大学,2007.
[6] 谭晓军.电动汽车动力电池管理系统设计[M].广州:中山大学出版社,2011:88-120.
[7] 岳仁超.电池管理系统的研究[D].北京:北方交通大学,2010.
[8] 董振华.电动汽车锂电池管理系统设计[D].北京:北方工业大学,2010.
[9] 陈勇军.磷酸铁锂电池建模及SOC算法研究[D].哈尔滨:哈尔滨工业大学,2011.
[10] DU J,LIU Z,WANG Y,et al.State of charge estimation for Li-ion battery based on model from extreme learing machine[J].Control Engineering Practice,2014,2(6):11-19.
[11] LIU H,XU Q,HU Y,et al.SOC Estimation of lithium iron phosphate batteries based on adaptive Kalman flters[J]. Joural of Chongqing University,2014,37(1):68-74.
[12] 汤恩恩.纯电动汽车电池管理技术的研究[D].武汉:武汉理工大学,2014.
[13] 何正伟,付主木. 混合动力汽车电池管理系统SOC估算策略[J]. 电源技术,2013,37(1):1 003-1 021.
[14] GAO M,HE M,XU J,et al.Sigma point Kalman flter based SOC estimation for power supply battery[J].Transactions of China Electotechnical Society,2011,26(11):161-167.
[15] WU T,HU T.Study of SOC estimation algorithm of power battery based on UKF[J].Power Electronics,2014,48(4):23-26.
