直升机在不同海情不同吨位舰船起降舰面共振研究
2018-05-23周华
周华
(航空工业直升机所,江西景德镇333001)
0 引言
舰载直升机以舰船为基础,其使用环境与陆基明显不同。舰船随浪起伏,其运动是多自由度的,不仅有横摇、纵摇、升沉,而且还有横荡、纵荡、摇艏,有时舰船摇晃的角度可达到30°~40°以上。舰船运动使起落架出现正负过载,起落架刚度、阻尼特性与地面静载不同。在这种环境下,舰载直升机舰面起降开车动不稳定性等将会产生变化。舰船随风浪的运动是随机过程,它并不与海浪同步。在相同风浪下,舰船的质量、大小、航速不同,其运动也将不同。
本文选取2种不同吨位的舰船,选取类似停放点位置进行计算。目前国内外舰载直升机的海上自由起降的海情要求最高普遍为5级。选取两型舰船在5级海情下运动参数,对比计算吨位对舰面共振特性的影响。另外,选取小吨位舰船,对比计算不同海情(3级海情和5级海情)对舰面共振的影响。
1 计算方法
由于舰船对于不同海情下的摇晃和沉浮的周期为8~12 s,而直升机不稳定边界频率约大于2.5 Hz,周期为0.4 s左右,两者相差20多倍,因此可以认为在短暂的时间内由舰船摇晃运动产生的作用于直升机的惯性载荷为不变载荷。这个载荷和机体重量一起对起落架系统的静平衡位移和刚度阻尼产生影响。
直升机在舰面上的模型如图1所示。

图1 直升机舰面运动数学模型
随着舰的纵摇和横摇等不同姿态,由起落架承受机体重量及舰船摇晃及沉浮运动作用于直升机的惯性载荷时,将产生新的平衡位置,静平衡方程为:
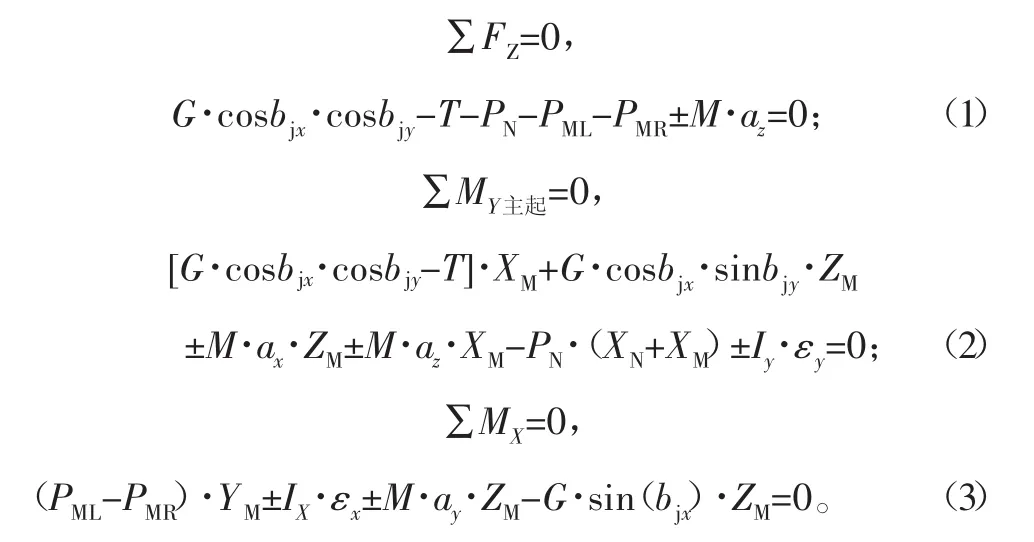
解方程得前起上的载荷为
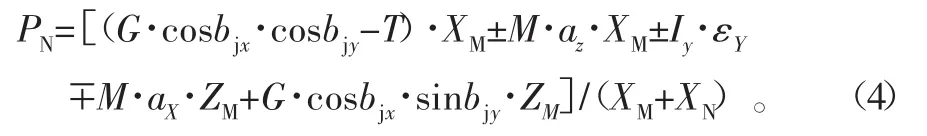
后起上的载荷为

式中:M为全机质量;G为全机重量;ax、aY、az分别为着舰处直升机重心由舰摇晃引起的X、Y、Z向加速度;εX、εY分别为舰横摇和纵摇角加速度;bjx、bjy分别为舰横摇和纵摇角。IX、IY为全机绕重心的X轴和Y轴的转动惯量。
建立机体8自由度(机体X、Y、Z三个方向平动和旋转共6个自由度,以及旋翼摆振平面2个自由度)的运动方程,并对方程进行整理,按如下形式列成二阶齐次线性微分方程组(矩阵形式):

式中:X=[φx,φy,φz,x,y,z,ξx,ξy],φx、φy、φz分别为横滚、俯仰、偏航运动自由度,x、y、z分别为航向、侧向和垂向平动自由度,ξx、ξy为桨叶摆振平面2个自由度;M、K、C均为8×8的矩阵,M为机体质量和惯量组成的质量矩阵,K为起落架和减摆器等刚度组成的刚度矩阵、C为起落架和减摆器等阻尼组成的阻尼矩阵。矩阵部分系数如下:
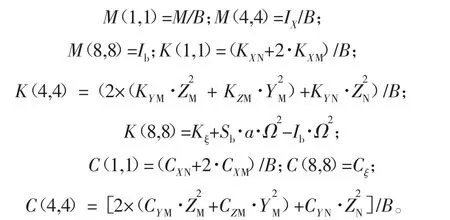
式中:B为主桨叶片数的一半;Sb、Ib分别为单片桨叶绕摆振铰的静距和转动惯量;KXN、KYN、KZN、KXM、KYM、KZM分别为前、主起落架X、Y、Z向刚度;Kξ为减摆器角刚度;a为桨毂中心到摆振铰的距离;CXN、CYN、CXM、CYM、CZM分别为前起落架X、Y向阻尼、主起落架的X、Y、Z向阻尼。
对方程(6)求特征值,根据特征值实部的正负判断舰面共振是否收敛,负则稳定,正则不稳定。
2 两型舰船5级海情下舰面共振特性对比
大吨位舰船(以下简称“舰1”)和小吨位舰船(以下简称“舰2”)运动参数见表1。
用某型直升机参数按第1节所述方法进行舰面共振计算,设定若主机轮在某升力下压缩量小于5 mm,则视其即将离舰,终止更大升力的计算。
典型频率和阻尼曲线见图2和图3,阻尼图纵坐标以0为界,大于0表示不稳定。

表1 两型舰船5级海情舰首位置运动参数
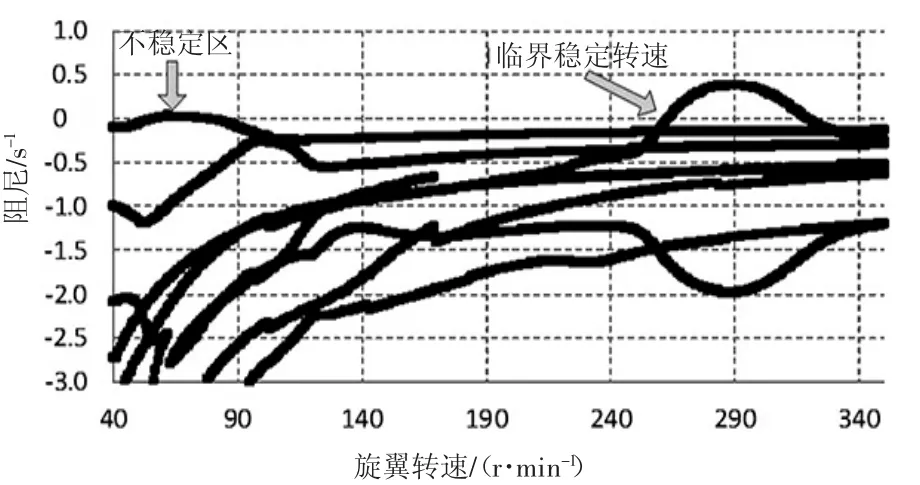
图2 大重量典型阻尼曲线(舰2)

图3 大重量典型频率曲线(舰2)
部分计算结果见表2~表3。“不稳定区”(D1)指在额定工作转速之内的不稳定转速区,“临界稳定转速”(W1)指额定工作转速之外的不稳定区域左边界。
用计算结果绘制该型直升机安全转速图,见图4,菱形线为舰2,圆形为舰1。
由图4可知,舰1低转速不稳定区范围小于舰2,舰1临界稳定转速高于舰2。说明在大吨位舰上起降,在额定工作转速范围内,不稳定转速区较小;在额定工作转速之外,临界稳定转速较高。同等海情条件下,大吨位舰比小吨位舰的舰面共振稳定裕度更高。
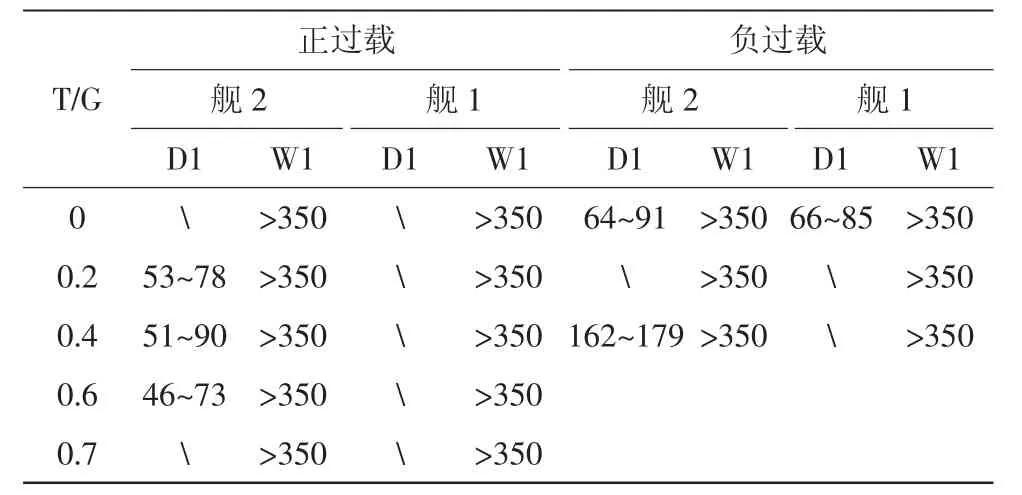
表2 小重量5级海情 r/min

表3 大重量5级海情 r/min

图4 两型舰起降安全转速图
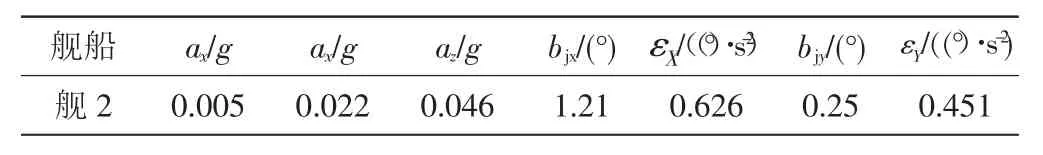
表4 3级海情下舰2的舰首位置运动参数

表5 大重量3级和5级海情正过载 r/min
3 不同海情的舰面共振特性分析
用同一直升机(大重量)分别计算3级和5级海情下,舰2自由起降舰面共振裕度。5级海情参数见表1,3级海情参数见表4。
部分计算结果见表5。
由表5可知,该型直升机大重量状态,在3级海情下,当升重比T/G>0.7,须迅速起飞;在5级海情下,当T/G>0.5,就须迅速起飞。并且,3级海情下,不稳定区主要出现在升力较大的时候,而5级海情下,不稳定区主要出现在升力较低的时候。海情级别越高,允许的舰面起降升力上限就越低。
4 结论
本文介绍了直升机舰面共振的分析方法,并分析不同吨位舰船、不同海情对直升机舰面共振特性的影响,物理概念清晰,计算结果可靠,可用于指导舰载型直升机的设计研制。
[参 考 文 献]
[1] 徐敏,张晓谷.一种分析滑橇式起落架直升机“地面共振”的方法[J].南京航空航天大学学报,2004,36(4):533-538.
[2] 航空航天工业部科学技术研究院.直升机动力学手册[M].北京:航空工业出版社,1991.
