电动汽车车架的随机振动分析

2018-05-23张硕龙海洋裴未迟李耀刚叶晓濛楚京

机械工程师 2018年5期

张硕，龙海洋，裴未迟，李耀刚，叶晓濛，楚京

（华北理工大学机械工程学院，河北唐山 063009）

0 引言

随着能源危机的进一步升级，作为传统交通工具的替代品，电动汽车得到了世界各国的关注。电动汽车更因其自身噪声低、能源利用率高、污染小等优势使人们找到了未来解决能源问题的新出路。

而作为整车的受力基体部分，车架的振动参数无疑是衡量电动汽车稳定性与安全性的重要指标。在车辆行驶过程中，路面不平度不仅使乘客感到不适，也会导致车架结构或车架上零件的损坏，从而降低车辆的使用寿命[1-3]。电动汽车行驶在城市沥青路面上时，受到来自路面的随机激励，若激励过大或使整车发生共振，必然会引起整车波动[4]，将导致电动汽车产生疲劳破坏，因此电动汽车的随机振动分析具有一定的实际研究价值。

1 随机路面仿真模型的获取

随机振动是由路面不平度引起的，其激励过程不可用确定的函数来描述，但可采用概率统计方法来研究。对车架进行随机振动分析，主要是研究车架在随机激励过程中的响应特性[5-6]。

目前，主要应用谱分析法来分析随机载荷。功率谱密度分析（PSD）作为谱分析的一种类型，也可称为随机振动分析[7]。文中利用位移功率谱密度分析方法对车架进行随机振动分析。

车辆平顺性有效的路面波长通常在0.35 m＜λ＜91 m，即空间频率0.011m-1＜n＜2.83m-1，常用车速为36～108km/h，即u=10～30 m/s。所以，可以保证时间频率范围0.33～28.3 Hz，其覆盖车身固有频率1～2 Hz和车轮固有频率10～15 Hz。

由于功率谱密度具有单位频带内的功率的含义，故空间频谱密度和时间频谱密度可分别表示为：

式中，为在Δn范围内的功率大小。所以和Gq（f）两者的关系为

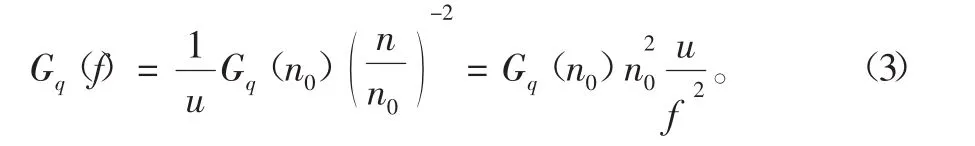
同理可得

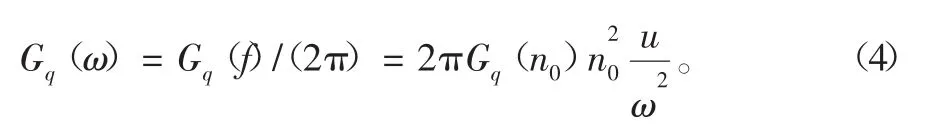
在城市沥青路面上，多座位电动汽车的平均行驶速度为40 km/h。在式（4）中当ω→0时，Gq（ω）→∞。因此实用功率谱密度为

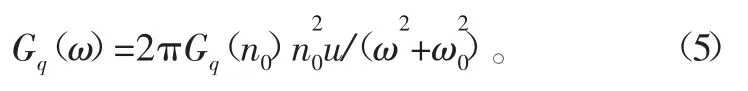
式中：ω0为最低截止角频率。

上式可看为白噪声激励的一阶线性系统的响应。由随机振动理论可得

式中：H（ω）为频响函数。

由上式可推出路面不平度的微分方程：

式中：q（t）为路面不平度函数，m；W（t）为均值为零的高斯白噪声；n00为路面空间截止频率，n00=0.11 m-1。

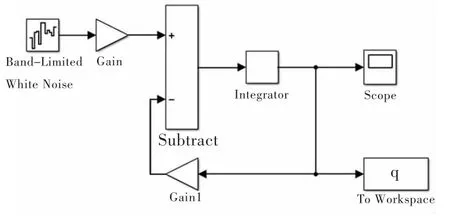
图1 路面不平度时域模型

根据式（7），应用 Matlab/Simulink软件建立时域仿真分析模型来表示路面不平度，如图1所示。

在进行仿真时，根据需要输入路面不平度系数和车速，便可得到相应情况下的时域路面激励信号。B级路面车速为40 km/h的路面激励信号如图2所示，B级路面不平度功率谱密度如图3所示。

图2 B级路面时域激励信号

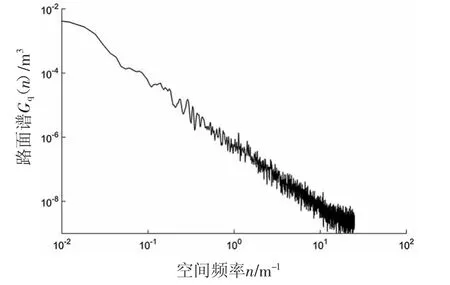
图3 B级路面不平度功率谱密度

2 车架的随机振动分析

以车架满载弯曲下的动态分析结果为基础在Workbench中对车架进行边界约束，并加载B级路面上的随机位移功率谱密度对车架进行谱分析求解[9]。

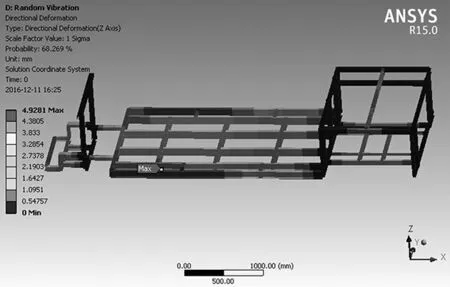
图4 随机振动分析车架的等效应变云图

多座位电动汽车以40 km/h车速在B级路面上行驶时，车架的位移变形云图如图4所示。

由图4可知，车架的最大变形发生在车架中部左右2个主横梁上，最大变形值为4.9281mm，在变形量最大位置选择节点进行位移响应分析，第1个节点为车架中部最右侧横梁与第1根短纵梁交接处；第2个节点为车架中部最左侧横梁与第1根长纵梁交接处；第3个节点为车架中部最左侧横梁与第1根短纵梁交接处；利用Workbench分析得到3个节点的位移响应谱分布曲线如图5所示。

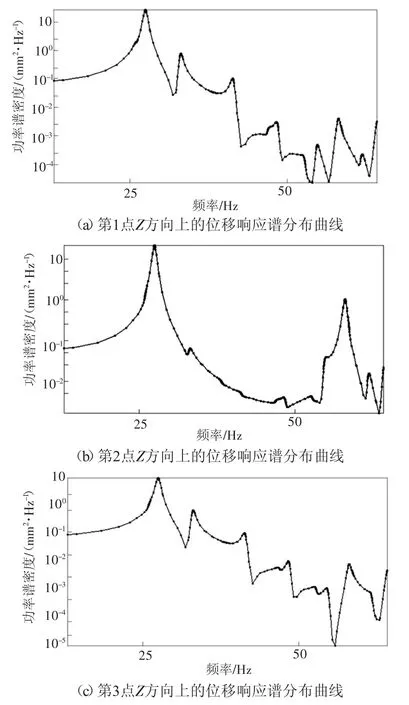
图5 3个点的位移响应谱分布曲线

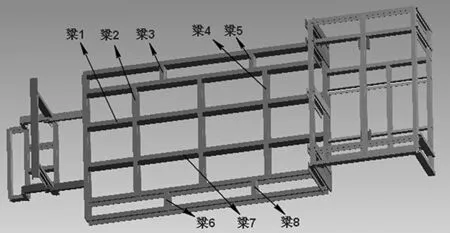
图6 梁的位置示意图

由图5可知，3个点均在26.762 Hz时出现位移极大值，该频率为车架满载下动态分析的第3阶固有频率，由车架试验模态分析结果车架第5阶22.64 Hz和第6阶29.19 Hz可知，车架的固有频率与该频率相差较小，因此在电动汽车整车设计中应避免其他部件的振动频率接近该频率，避免共振耦合的发生[10-12]。

3 结构优化设计

车架应变云图显示该车架最大应力发生在车架前部的立梁与连接前部和中部的方钢交接位置，车架其他位置应力均在52 MPa以下，说明这些位置选用的材料有较大富余地满足使用要求，应考虑轻量化研究[10]。

车架尾部放置电池位置最大变形在1 mm以下，且组合应力在37 MPa以下，可以将此处的槽钢换为其他轻质型钢，以减小车架质量；由车架位移分布图可知车架尾部载客位置中间的纵梁变形较明显，且在车架满载弯曲工况下梁扭曲变形过大，应该增加支撑梁；原车架中部载客位置的槽钢选用的是10#槽钢，由分析云图可知，最大变形集中在车架中部的中间一排载客位置，另外2排载客位置位移及应力相对较小，故保留车架主梁来承担载荷，将梁1～8换为其他轻质型钢（梁1～8位置如图6所示）

图7 优化后车架静力分析

考虑到可选角钢型号较多，故应用优化模块实验设计（DOE—Design of Experiment）探究设计参数与目标参数间的关系[13]，再对产品进行深一步的多目标优化，确定产品的优化方案，以保证产品的综合性能达到最好，最终将车架梁1～8由槽钢换为100 mm×100 mm×6 mm的角钢，得到满载弯曲工况下车架的位移变形及应力分布图如图7。

由图7可知，车架尾部放置电池位置可以满足强度刚度要求，车架尾部载客位置中间的纵梁变形状况明显得到改善，最大应力降低，一阶频率超出了路面激励范围[14-15]，有效提高了车架动态特性。

4 结论

本文介绍了车架随机振动分析过程，结合车架满载下的动态分析结果表明：车架位移变形较大，应力过大，低阶固有频率偏低。结合力学理论知识提出改进方案，对改进后车架再次进行有限元分析，车架变形、应力均减小，低阶固有频率提高。在Workbench车架的随机振动分析中，得到车架在路面激励作用下在26.762 Hz时位移响应最大，为车架的结构改进提供重要的理论依据。

[参考文献]

[1] 单承标.电动汽车车架结构优化设计分析[J].国防制造技术,2016(1)：51-53.

[2] 钱洋,朱茂桃,郭佳欢.微型电动汽车车身的轻量化[J].机械设计与研究,2014(6)：146-150.

[3] 郝君起,陶元芳.混合动力电动汽车设计方案分析[J].机械工程与自动化,2010(6)：214-216.

[4] 刘杨.电动观光车车架结构分析及优化设计[D].长春：吉林大学,2007.

[5] 邵超城,刘强,龙飞永.纯电动汽车车架设计及有限元分析[J].机械设计与制造,2011(8)：39-41.

[6]侯军海.电动汽车桁架式车架结构的拓扑优化设计[D].太原：中北大学,2012.

[7]王青春,范子杰,洪在地,等.有限元方法及Midas软件在汽车结构分析中的应用[M].北京：机械工业出版社,2014.

[8]杨卓.低速纯电动汽车车架的轻量化研究[D].广州：华南理工大学,2014.

[9]FUKUSHIMA J,SUZUKI K,KIKUCHI N.Shape and Topology Optimization of a Car Body with Multiple Loading Conditions[J].SAE paper,2012,5(2)：36-40.

[10]武和全,辛勇,董学勤.某越野车车架有限元建模与刚度分析[J].机械设计与制造,2008(6)：15-17.

[11]张建,戚永爱,唐文献,等.基于有限元法的某卡车车架优化设计[J].机械设计与制造,2012(5)：48-50.