用Vivado HLS实现粒子滤波算法的硬件加速
2018-05-23高国栋
高国栋,林 明
(江苏科技大学 电子信息学院,镇江 212003)
粒子滤波算法(particle filter, PF)[1]发展于20世纪90年代,是一种蒙特卡洛方法和递推贝叶斯估计相结合的新型估计算法.在处理非线性、非高斯系统的状态估计方面具有明显优势,有效地克服了扩展卡尔曼滤波等方法的局限性.粒子滤波算法自提出至今,在理论上取得了显著成果,但很多研究还停留在理论仿真阶段,如何简化算法复杂度,提高运算速度,将粒子滤波算法用硬件实现,并应用于更多的领域,是当前粒子滤波的研究热点.硬件实现粒子滤波,为达到更高的滤波精度,往往需要更多的粒子数量,就意味着需要更大的计算量.PF算法引入了重采样步骤,削弱了粒子滤波可以进行并行处理的优势,重采样成为了PF算法实时性处理的瓶颈.GPF(Gaussiam particle filter)算法[2]是PF算法的改进算法,用重要性采样方法更新状态的均值和方差,免去了重采样步骤,使PF算法的并行运行成为可能.同时GPF算法无需存储每次迭代得到的所有粒子的状态和权重,减少了对存储空间的要求.因此在硬件实现方面,GPF算法比PF算法更具优势[3].所以文中选择GPF算法作为硬件实现的目标算法,并将其运用到一个典型的二维纯方位跟踪(2 dimensional bearing-only tracking,2-D BOT)非线性系统中.
为满足实时性要求,运用现场可编程门列(field-programmable gate array,FPGA),实现硬件并行流水线计算是一种有效方法.已经有很多学者对PF算法的硬件实现进行了研究,并都取得了一定成果.为了更利于PF算法的硬件实现,文献[4]中简化了PF算法,着重对重采样方法进行了改进,并根据算法给出了合理的FPGA实现方案.文献[5]中研究了拟蒙特卡洛-高斯粒子滤波算法的并行结构,并在此算法的基础上给出了FPGA硬件实现方案.文献[6]中给出了基于System Generator的PF算法硬件实现方案,首先根据算法搭建Simulink模型,然后转换为RTL代码.以上的PF算法硬件实现过程,是对具体算法具体分析,给出具体硬件结构,因而得到的硬件模块都具有比较高的性能和资源效率.从总的开发流程来看,以上粒子滤波IP核各实现过程可概括为算法从软件到硬件的转换过程.但由于在开发过程中不但要考虑算法的可行性,还要充分考虑硬件的可实现性,需要关注硬件设计的每个环节,开发效率并不是很高,属于传统的FPGA开发过程.
文中针对传统FPGA开发流程实现PF算法过程中出现的问题,提出了基于Vivado HLS 的GPF算法的硬件实现方法.该方法根据特定的综合优化策略,直接将C语言算法综合为具有期望结构的FPGA硬件模块.可以用少量的时间开发出具有同样高性能的硬件模块,因而具有比较高的开发效率,同时也具有较强的开发灵活性[7-8].
1 Vivado HLS设计介绍
Vivado HLS是Xilinx公司推出的最新一代FPGA设计工具,该工具可以把用C标准语言(C、C++或SystemC)描述的算法模块编译并综合成寄存器传输级(RTL)硬件IP模型,产生实现硬件加速所需要的HDL代码,直接用于在FPGA中实现.在硬件开发过程中,开发者只需专注于算法规格、算法C语言实现以及算法宏观架构,Vivado HLS工具会自动考虑FPGA的微观架构.
用C标准语言设计出算法模块,辅以相应的约束文件和优化策略,同时给出测试模块行为和功能的C测试文件(C Test Bench).经过验证算法的正确性后,就可以进行RTL级综合生成,得到RTL代码.使用Vivado HLS内置仿真工具XSIM或者第三方仿真工具Modelsim进行功能仿真,进一步验证设计的架构行为和功能.得到的RTL代码可直接用于Xilinx设计开发环境,做系统集成、仿真以及生成bit文件.
Vivado HLS主要根据3种参数来描述模块的性能[9]:数据初始化间隔(Initiation Interval,II)、数据延迟(Latency)和面积(Area).其中II代表模块接收相邻两次新的输入数据之间的时钟间隔,更小的II意味着更大的数据吞吐量;Latency指模块从输入新的数据到给出所有输出数据的延迟时钟数,更小的Latency表示更快的计算速度;Area指模块所占用的逻辑资源.HLS默认以II、Latency、Area为优先级顺序,对C算法进行综合实现.
2 基于GPF算法的纯方位跟踪
BOT模型常用于被动跟踪系统中,由于其隐蔽性好,抗干扰性强,历来是研究的热点和难点.目前对BOT问题研究大多基于扩展卡尔曼滤波器及其各种变形来进行.实际上由于系统本身的弱观测性和状态空间模型的强非线性,这些传统方法在精度方面往往不能满足要求.GPF算法处理BOT问题有很好表现.文中只研究在高斯背景下的纯方位跟踪问题[4],其系统噪声和量测噪声都是高斯白噪声.
在直角坐标系下,BOT模型的系统状态方程和观测方程分别为:

(1)


(1) 初始化.k=0时刻初始化目标状均值x(0)=[xp(0),xv(0),yp(0),yv(0)]T;初始化状态方差Σ(0)=[Σx(0),Σvx(0),Σy(0),Σvy(0)]T.
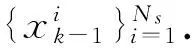
xi(k-1)~N[x(k-1),Σ(k-1)]
(2)

xi(k)=Φxi(k-1)+Γw(k-1)
(3)
计算权重:

(4)
(4) 权值归一化.得到每一个粒子的权值后,再对所有权值归一化:
(5)
(5) 计算估计值.
(6)
(6) 计算k时刻的协方差.
(7)
(7) 返回到第(2)步进行迭代计算.
当Ns数量较大时,单步迭代计算将耗费大量时间.为了缩短计算时间以及减少硬件资源的利用,获得更高的性能,文中从以下几个方面对算法进行简化与改进:① 预先计算步骤(3)中的常数项,把结果直接代入算法中;② 去掉权值归一化步骤,将除法运算转变为乘法运算,再把步骤(3)和步骤(5)的循环合并为一个大循环;③ 将以上算法关于矩阵的计算变为标量计算,以降低计算的复杂度;④ 尽量减少算法内部数组和顶层模块端口的读写操作,可以通过设定内部缓存解决这样的问题;⑤ 使用Vivado HLS任意精度数据类型[9],根据实际需要合理设定变量位宽,从而获得更快的计算速度和更少的资源占用;⑥ 尽量使用Vivado HLS提供的针对硬件优化的C库函数,在以上算法中,有乘法、除法、指数运算和反正切运算等,这些运算可直接从Vivado HLS数学运算库中调用.
设定目标初始状态均值x(0)=[1, 0.3, 3, 0.3]T;初始状态方差Σ(0)=[0.01, 0.002, 0.01, 0.002]T;系统噪声的方差Σw=[0.004, 0.004]T;量测噪声的方差Σv=0.000 5;T=1 s;量测点位于原点,仿真时间为50 s.对以上算法进行多次Matlab仿真,仿真结果表明该算法具有良好的跟踪效果.图1给出了其中某次仿真结果.
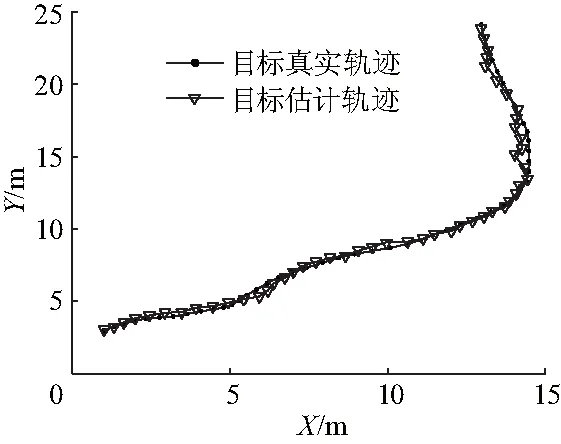
图1 2-D BOT模型的GPF算法Matlab仿真结果Fig.1 Matlab simulation results of GPF 2-D BOT
3 设计实现
GPF算法的单次滤波流程如图2.整个算法流程划分为5个任务步骤:任务1对端口数据预处理;任务2是一个循环,用于对粒子状态和计算粒子权重进行累加;任务3计算权重和的倒数并给出最终的状态估计;任务4也是一个循环,用于计算粒子状态方差的累加和;任务5计算最终的状态方差.文中以C++为描述语言,根据图2,给出基于GPF算法的2-D BOT模型的软件实现.
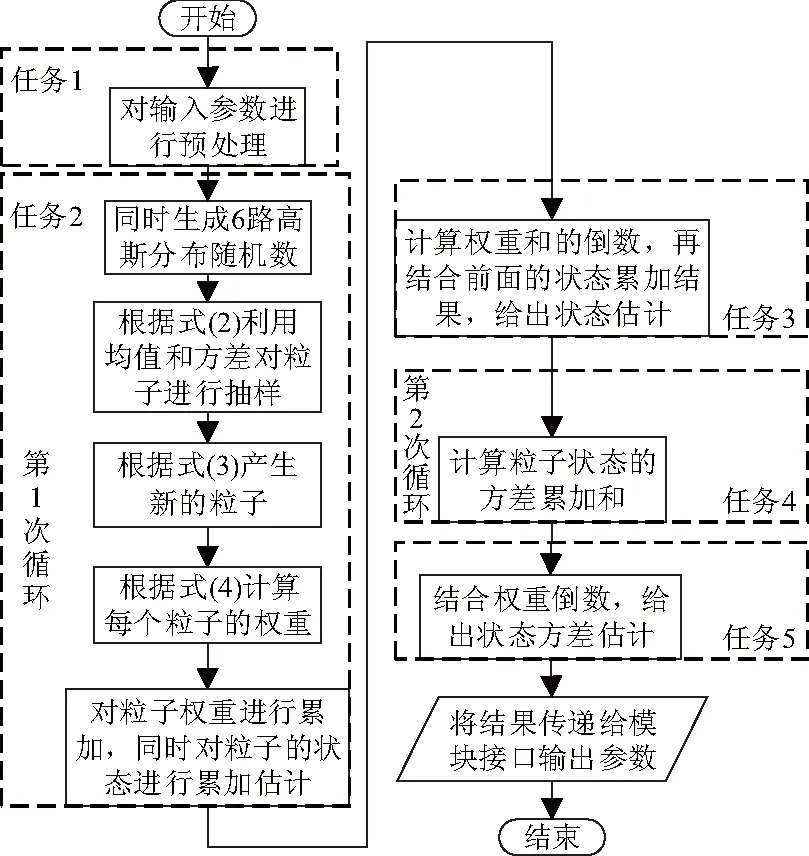
图2 2-D BOT模型的GPF算法流程Fig.2 Flowchart of implementation of GPF 2-D BOT
3.1 顶层模块设计
设计的顶层模块为State gpf-hls(ObsvType ZObserve, State Previous-state),其中输入参数ZObserve为当前时刻的观测值,Previous-state为前一时刻的状态,State为结构体类型:
typedef struct{
StateType Position-state[4];
StateSigmaType Sigma-state[4];
}State;
其中成员数组Position-state[4]用于存放状态均值,Sigma-state[4]用于存放状态的方差.函数的返回值是State类型,返回同样的信息.设计中将粒子数定义为宏变量,以便于方便修改粒子数量.
3.2 高斯随机数生成
基于GPF算法的2-D BOT模型需要同时产生6路均值为0、方差为1的高斯随机数.在FPGA中产生的高斯随机数通常都由均匀随机数转换得到.根据文献[11],首先运用m序列法产生均匀随机数,然后再运用Box-Muller方法结合非均匀量化查表法得到高斯随机数.
高斯随机数子函数为:
void awgn-generator(
ap-int< NOISE-WIDTH> &noise0,
ap-int< NOISE-WIDTH> & noise1,
ap-int< NOISE-WIDTH> & noise2,
ap-int< NOISE-WIDTH> & noise3,
ap-int< NOISE-WIDTH> & noise4,
ap-int< NOISE-WIDTH> & noise5)
该函数以参数引用的方式返回6路高斯随机数,数据类型是位宽为NOISE-WIDTH的有符号整形,通过设定小数点位置,就可以得到不同的幅度值.通过C/RTL协同仿真,波形如图3:

图3 6路高斯随机数波形Fig.3 Waves of 6-way Gaussian white noise generator
3.3 综合实现
当开发者没有添加任何综合优化策略时,Vivado HLS采用自带的默认策略进行综合实现[11].例如,C算法中的循环(Loop)默认不展开,每一次循环计算在同一个硬件单元实现,具有完全一样的状态.然而当算法的时序很复杂、计算量很大时,这些默认策略的综合结果往往不能满足设计要求.设计中首先选择目标器件xc7z020clg484,粒子数Ns分别为512,1 024,2 048,仅采用Vivado HLS的默认策略进行综合,得到表1数据延迟报告和表2资源利用报告.
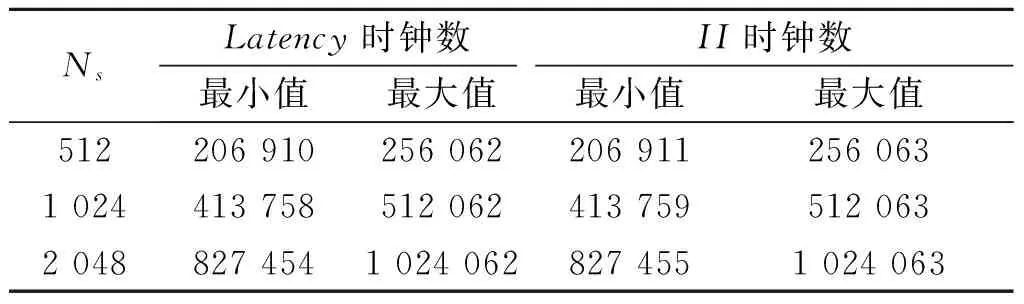
表1 Vivado HLS默认策略综合的数据延迟报告Table 1 Summary of Latency with default directives

表2 Vivado HLS默认策略的资源利用报告Table 2 Summary of utilization with default directives
由于表1中的Latency和II在同一种粒子数量下都近似相等,可以推断综合出来的模块并不能以并行流水线方式执行.而且根据表1中的数据,当系统时钟频率为100 MHz,粒子数为512时,滤波(采样)速率约为109 Hz,数据延迟约为2.3 ms,这样的速率低于DSP处理速率[12],失去了用FPGA硬件实现PF算法的优势.所以必须采用合理的综合优化策略,以获得更高的数据吞吐量和运算速度.
Vivado HLS提供丰富的综合优化策略,用户可以使用不同的策略来调整和控制内部逻辑和I/O行为,以充分利用硬件并行优势,获得更高的性能.在图2的算法流程图中,数据从任务1依次传递到任务5,且后一个任务仅对前一个任务有数据依赖关系,所以在任务层面可以采用数据流-流水线策略.图4显示了模块在任务层面上的流水线运行方式.

图4 任务层面上的流水线处理Fig.4 Pipeline structure on the task hierarchy
pipeline优化策略实现任务内部流水线操作,能实现子任务(函数、循环)最大化并行运行,最大程度降低II和Latency.在本设计中,将该策略运用到任务2的循环中,这样单次循环中的各项运算都将以并行方式运行,如果再对循环中的某些运算辅以其他策略,如inline,resource等,进入相邻两次循环的时间间隔就可以降低到1个时钟周期,即LoopII=1.最终的流水线效果如图5,其中Ns代表循环次数,整个任务的初始化间隔FunctionII=Ns.

图5 循环的流水线操作Fig.5 Pipeline structure on the loop hierarchy
然而在某些情况下,例如在单次循环中存在对存储器读操作时,因为读存储器需要多出一个时钟来提供地址,pipeline策略就不能把LoopII降为1,而最低只能降到2,此时该任务的FunctionII为2Ns,可能就成为整个模块数据吞吐量和运算速度的瓶颈.这时为了抵消这样的读操作瓶颈,除了采用Pipeline策略外,还要对该循环采用部分展开(partially unroll)策略,并设定展开因子(unroll factor)为2,这样总的循环次数减半,单次循环内并行的运算操作加倍.同时把循环内的要读的数组指定为双端口RAM,以满足单次循环2路并行读操作,这样就可以把FunctionII降低为Ns.本设计中的任务4就采用这样的策略,总体结构前后对比如图6.

图6 任务4采用partially unroll策略的结构转变示意Fig.6 Changes of the structure with partiallyunroll directive of task four
inline优化策略消除子模块与上层模块的层次边界,免去子模块的频繁读写调用,能使上层模块获得更好的性能.本设计中,把该策略用于运算操作比较少而调用很频繁的函数,如sqrtf(),atan2f(),expf()等.resource优化策略能为数组、运算操作符和函数接口等分配特定的资源类型,从而获得更高的资源效率和运算性能.例如,对某些乘法操作指定为DSP48乘法宏单元,对某些数组变量指定为双端口块RAM(RAM-2P-BRAM),以增加并行度.主要使用的综合优化策略如表3.

表3 本设计主要使用的优化策略Table 3 Main specified directives of this design
选择目标器件为xc7z020clg484,并且将粒子数Ns分别设定为512,1 024,2 048,根据表3中的策略,综合得到如表4、5.

表4 使用优化策略综合后的数据延迟报告Table 4 Summary of Latency with specified directives

表5 使用优化策略综合后的资源利用报告Table 5 Summary of utilization with specified directives
根据表4中的Latency和II的关系,可推断该模块能以并行流水线方式运行.表1、4同时说明,当粒子数量成倍增长时,Latency和II也大致成倍增长.但由于流水线结构的原因,表4中Latency和II增加的相对幅度小于2倍.进一步比较表1、4可知,当使用自定义优化策略后,系统的Latency和II大幅度下降,运算速率的数据吞吐量得到极大地提高.表2、5说明,更快的速度占用更多的资源.当系统时钟为100 MHz,粒子数量为2 048时,滤波速率约为48.8 kHz,数据延迟约为31.6 us,是同等条件下文献[4]中最好情况32 kHz的1.5倍.
3.4 C/RTL协同仿真
在Vivado HLS Test Bench目录下创建测试文件,在该文件中编写main()函数,以反馈调用的方式调用顶层函数:
for (i=1;i { state-estimated[i]= gpf-hls(Z[i],state-estimated[i-1]); } 函数中:T为仿真时间;数组Z[T]中存放观测值;数组state_estimated[T]中存放每次迭代的估计结 果.按照仿真初始值设定模块的初始状态state-estimated[0].在调用仿真之前,通过C++文件操作,把观测值从文件test-Z.txt中读入到数组Z[T]中.在仿真结束后,再把state_estimated[T]内容写入到文件中,用于分析校验. 根据Vivado HLS 开发流程,在创建完算法的C++语言描述文件和测试文件后,先后执行C simulation命令和C/RTL Cosimulation命令,分别从软件层面和硬件层面对算法进行验证.当粒子数量为1 024时,根据式(8)计算算法估计的均方根误差(root mean squared error, RMSE) (8) 表6 算法在不同仿真平台上跟踪性能仿真结果比较Table 6 Comparison of tracking performances of different simulation platforms 表6中,Vivado HLS C simulation和Vivado HLS RTL simulation仿真平台的仿真结果和Matlab的仿真结果很接近,说明在HLS工具中用C++语言描述的GPF算法及其综合得到的RTL模块功能的正确性.进一步观察可发现,C simulation和RTL simulation的仿真结果完全一致,这是因为产生伪随机数的RTL硬件模块是由C函数直接综合得到的,而两者采用相同的随机数种子,所以得到伪随机数序列是完全一样的,因而滤波过程中得到的数据完全一致. 图7为RTL仿真波形,在0.135 2 us时刻模块启动,开始从端口Previous-state读入数据.在17.255 us时刻,从输出端口输出结果. 图7 RTL仿真波形Fig.7 Waves of RTL simulation 在10.585 2 us时刻,模块从输入端口读入新的数据,并在27.695 us时刻输出结果.在每次迭代计算结束之前,就从输入端口读入新的数据,由此可见文中设计的模块以流水线方式运行.图8为C/RTL协同仿真结果,C仿真估计轨迹和RTL硬件仿真估计轨迹完全重合,这说明最终得到的RTL模块功能与软件仿真一致,能够实现对目标的跟踪. 图8 2-D BOT模型的GPF算法C/RTL协同仿真结果Fig.8 C/RTL cosimulation results of GPF 2-D BOT 按照图1中的开发流程来对GPF算法进行实现,主要有HLD代码编写、代码修改优化和仿真校验3个步骤.本设计中运用HLS工具进行开发也同样有这3个步骤.表7为二者在开发周期上的比较. 表7 两种方法在开发周期上的比较Table 7 Simple comparison between two methodson development cycles 从表7可以看出,用HLS方法对PF算法进行硬件实现能显著加快开发进程,使开发者能有更多的时间和精力研究原型算法的改进. (1) 运用Vivado HLS工具实现GPF算法的关键是灵活运用多种综合优化策略.根据实际需要,不同的综合策略能得到不同硬件结构.运用pipeline策略及其辅助策略实现的并行流水线结构,能很好地满足PF算法实时性要求. (2) 文中实现的GPF算法硬件结构在保证运算准确的前提下,达到了较高的数据吞吐量和较快的数据运算速度. (3) 文中运用Vivado HLS工具实现GPF算法,大部分时间和精力放在了算法的合理性以及宏观的硬件架构上,只有少部分放在了微观的硬件实现细节上,因而具有较高的开发效率. (4) 文中提出的实现方法对其他复杂软件算法的硬件化加速具有重要的指导意义. 参考文献(References) [ 1 ] ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188. DOI:10.1109/78.978374. [ 2 ] KOTECHA J H, DJURIC P M. Gaussian particle filtering[J]. IEEE Transactions on Signal Processing, 2003, 51(10): 2592-2601. DOI:10.1109/tsp.2003.816758. [ 4 ] 洪少华, 史治国, 陈抗生. 用于纯方位跟踪的简化粒子滤波算法及其硬件实现[J]. 电子与信息学报, 2009, 31(1): 96-100. HONG Shaohua,SHI Zhiguo,CHEN Kangsheng. Simplified algorithm and hardware implementation for particle filter applied to bearings-only tracking [J]. Journal of Electronics and Information Technology, 2009, 31(1):96-100.(in Chinese) [ 5 ] 李倩, 姬红兵, 郭辉. 拟蒙特卡罗-高斯粒子滤波算法研究及其硬件实现[J]. 电子与信息学报, 2010, 32(7): 1737-1741. LI Qian, JI Hongbing, GUO Hui. Reasearch and hardware implementation of Quasi-Monte-Carlo Gaussian particle filter[J]. Journal of Electronics and Information Technology, 2010, 32(7):1737-1741. (in Chinese) [ 6 ] 毛丽民, 卢振利, 浦宇欢, 等. 基于FPGA实现粒子滤波算法的实时细胞跟踪系统设计[J]. 红外技术, 2014, 36(5): 389-393. MAO Limin, LU Zhenli, PU Yuhuan, et al. Design of a real-time cell tracking system by implementation of particle filter algorithm with FPGA[J]. Infrared Technology, 2014, 36(5):389-393. (in Chinese) [ 7 ] COUSSY P, CHAVET C, BOMEL P, et al. High level synthesis from algorithm to digital circuits [M]. [S.l.]: Springer, 2008. [ 8 ] XILINX Inc. Introduction to fpga design with vivado high-level synthesis [EB/OL]. (2013-07-02) [2016-03-20].http://www.xilinx.com/support/documentation/sw_manuals/ug998-vivado-intro-fpga-design-hls.pdf. [ 9 ] XILINX Inc. Vivado design suite user guide high-level synthesis [EB/OL]. (2015-02-24) [2016-03-20].http://www.xilinx.com/support/documentation/sw_manuals/xilinx2015-2/ug902-vivado-high-level-synthesis.pdf. [10] 陈鹏, 钱徽, 朱淼良. 一种快速高斯粒子滤波算法[J]. 华中科技大学学报(自然科学版), 2008, 36(s1): 291-294. CHEN Peng, QIAN Hui, ZHU Miaoliang. A fast Gaussian particle filtering algorithm [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2008, 36(s1): 291-294.(in Chinese) [11] GHAZEL A, BOUTILLON E, DANGER J L, et al. Design and performance analysis of a high speed AWGN communication channel emulator[J]. IEEE Pacific Rim Conference on Communications, Computers and Signal Processing,2001:374-377. DOI:10.1109/pacrim.2001.953647. [12] 余纯. 基于硬件实现的粒子滤波改进算法研究[D]. 北京: 北京交通大学, 2008.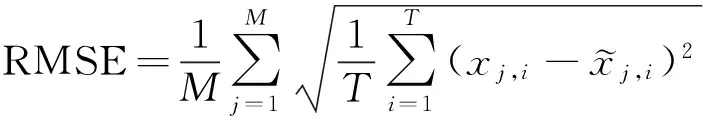




3.5 开发效率比较

4 结论

