线性代数中矩阵的应用案例

刘媛媛

近几十年来，随着科学技术的发展，特别是计算机技术的发展，数学的应用领域由传统的物理领域迅速扩展到非物理领域，在发展高科技，提高生产力水平和实现现代化管理等方面的作用越来越明显，这就需要我们将实际问题转化为某一个数学问题，然后使用某种适当的数学方法去解决［1］.线性代数是数学的一个分支，矩阵是线性代数的一个很重要的组成部分［2］.矩阵是由数字按照行和列排成的一个数字表格，同类表格之间往往存在诸多关系，表格当中的数据可以代表实际问题中的某种信息［3］，因此，可以利用矩阵数表中贮存的庞大信息处理解决许多实际生活中的具体问题［4］.本文充分利用矩阵的这一强大功能有效地解决了人口流动、工业增长、动物种群生态及密码编制四方面的具体问题.

1 人口流动问题

某城市及郊区乡镇共有50万人从事农、工、商工作，假设总人数在若干年内不会改变，经调查表明：

（1）在这50万的就业人员中，目前大约有25万人从事农业，约15万人从事工业，约10万人从事商业.

（2）在务农的人员中，每年大约有20%改为务工，10%改为经商.

（3）在务工的人员中，每年大约有20%改为务农，10%改为经商.

（4）在经商的人员中，每年大约有10%改为务农，10%改为务工.

现要预测1、2年之后从事农、工、商工作的人数，以及多年之后，从事各行业人员总数及发展趋势.

解 设xi,yi,zi表示第i年后分别从事农、工、商的人数，则x0=25,y0=15,z0=10，现在要求出x1,y1,z1和x2,y2,z2，并考察经过n年以后xn,yn,zn的发展趋势.

根据题意，可以列出一年后从事农、工、商的人员总数的方程为

即得到了一年后从事农、工、商的人数分别为22.9万人，16.9万人，10.2万人.

当n=2时，有

即得到了两年后从事农、工、商的人数分别为21.73万人，17.23万人，11.04万人.进而推得

即得到了n年后从事农、工、商的人数完全由An来决定.

在这个实际问题的求解过程中，充分利用了矩阵的乘法、转置等知识，将生活中的实际问题转换成了一个数学问题，通过求解这个数学问题进而解决了实际生活问题，将一个较为复杂的人口流动实际问题成功解决，可以看出矩阵往往是解决实际问题的工具，矩阵知识在实际问题的解决中发挥着重要作用［5］.

2 工业增长问题

考虑一个有关工业发展与环境污染的工业增长模型.设m是目前环境污染的程度，n是目前工业发展的程度，两者都由各种指标组成的单位来衡量.比如，对于污染，空气中一氧化碳的含量及河流中污染浓度等.设m′和n′分别是五年

而随后的10年、15年、…、5n年环境污染程度与工业发展水平分别为

初始值为m=4,n=2，由（1）式可以得到未来50年环境污染程度与工业发展水平的情况，如表1所示.后的环境污染程度及工业发展的水平.根据类似的经验，发展机构认为，可以用下面的线性模型来预测随后5年环境污染程度与工业发展水平的 情 况 为m′=m+2d，n′=2n+d. 记

为了分析上表中m和n的变化规律，先求矩阵A的特征根与特征向量.由于A的特征多项式为(x-3)(x+1).则A的特征根λ1=3 ，λ2=-1.对于特征根λ1=3 ，向量为-1的特征向量，即为3特征向量，即同样对于特征根-1，向量

设m=1,n=1，利用式（1）计算出5年、10年、…、5k年后环境污染与工业发展水平的关系式子为5k年

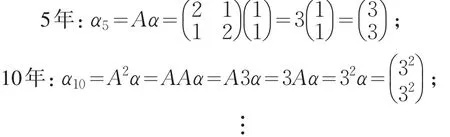
若设m=4,n=2，5k年后环境污染与工业发展水平之间的关系为从此式可以看出，当k比较大时，对整个结果的影响很小，可以忽略不计.

所以，当k较大时，5k年后环境污染与工业发展水平之间的关系式可被写作

设m=1,n=7为初始值，就可以得到20个5年后环境污染与工业发展水平之间的关系式为：由于此式中的最后一项在很大时可以忽略不计，因此

3 动物种群生态问题

考虑一个关于狐狸和兔子的生态模型.假设在没有狐狸的情况下，兔子的数量为P，一年的增长率为10%，下一年兔子的数量P′为1.1P.假设在没有兔子的情况下，狐狸的数量为Q，一年增长率为-15%，下一年狐狸的数量Q为0.85Q.当狐狸和兔子同时出现时，狐狸吃兔子，狐狸的数量增加，兔子的数量减少，建立模型如下：

令，将（2）式转换成用矩阵来表示的增长模型为

令P＝10，Q＝8，由模型（2）计算，经过一段时间后，狐狸和兔子种群的数量之间的数学关系如表2所示.

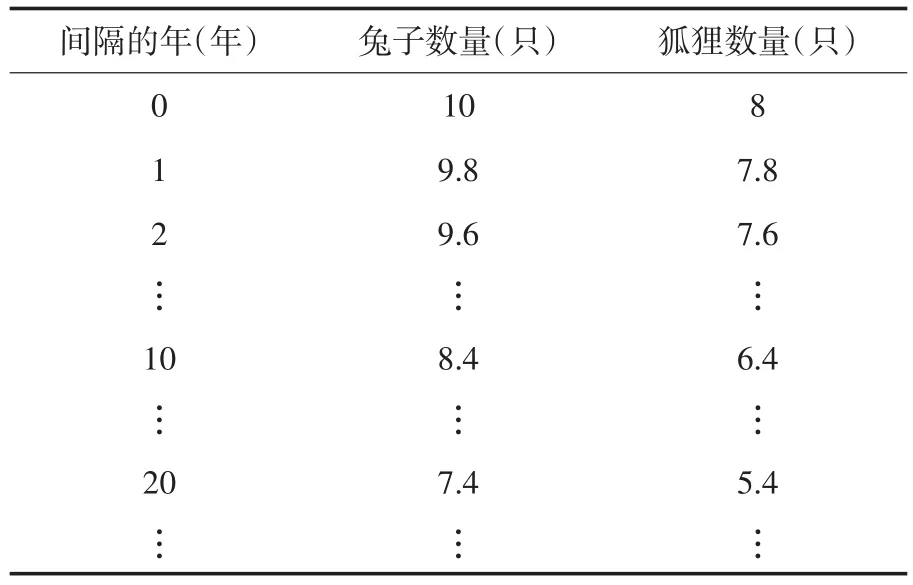
表2 狐狸和兔子种群之间的数量关系

此类问题可通过特征根和特征向量对上表所表示的性态进行分析.

由于B的特征多项式为fB(x)=，因此易求出它的特征根为λ1=1,λ2=0.95.

进而可求出特征根1的特征向量为.特征根0.95的特征向量为

设，求得a=2,b=4，则，因此经过n个时间段后，狐狸和兔子种群数量之间的数学关系为于是由一个稳定种群项和一个缓慢衰减的第二项组成的.因此，正如表中计算的结果所表示的趋势那样，狐狸和兔子的种群数量越来越趋向于4、6.

4 密码编制问题

密码学在通信及军事上都有重要的应用.在密码学中将信息代码称为密码，没有被转换成密码的文字信息被称为明文，将密码表示的信息称为密文.从明文向密文转换的过程叫加密，反之称为解密.

矩阵密码法是信息编码与解码的技巧，其中一种就是利用求逆矩阵的方法.先在26个英文字母与数字之间建立一一对应，比如

如果我们要使用上述代码发出信息“SEND MONEY”，则此信息的编码是19、5、14、4、13、15、14、5、25，其中5表示字母E，但是直接这样表示的编码很容易被别人破译.这时可以利用矩阵的乘法来对信息“SEND MONEY”进行加密，让其变成“密文”后再发出去，这样既可以增加非法用户破译的难度，又可以让合法用户轻松解密.如果一个矩阵A和其逆矩阵A-1中的元素均为整数，则可以利用这样的矩阵A来对信息加密，使加密以后的密文很难破译.例如取

信息“SEND MONEY”对应的9个数值便可排成下面的矩阵B

利用矩阵的乘积，则有则与之相对应的密文编码为 43、105、81、45、118、77、49、128、93.借此合法用户可以用A-1去左乘以上述矩阵，即可解密得到明文.

这个例子是矩阵乘法与逆矩阵的一个实际应用，将线性代数与密码学紧密联系起来.运用矩阵知识破译密码，进而运用到通信、军事等方面.可见矩阵的作用非常强大.

5 结论

该文给出了线性代数学科中的矩阵在人口流动、工业增长、动物种群生态及密码编制等实际问题中的应用.通过这些问题的成功解决可以看出，许多原本较为复杂的实际问题，如果能够有效利用矩阵这个工具，问题往往容易简单快捷地得以解决.其实矩阵还在其他诸如：生产成本核算、文献管理、电阻电路等许多与我们息息相关的实际问题中有较为广泛的应用，这些问题还有待于我们进一步去深入地研究和探讨.

：

［1］同济大学数学教研室.线性代数［M］.北京：高等教育出版社，2006.

［2］刘鹏.矩阵在数学建模中的应用举例［J］.楚雄师范学院学报，2006，21（6）：4-9.

［3］刘仲奎，杨永保.高等代数［M］.北京：高等教育出版社，2006.

［4］白梅花.矩阵及其乘法应用实例举例［J］.科技教育，2011（8）：21-23.

［5］王仲春.数学思维与教学方法论［M］.北京：高等教育出版社，1989.