看条件 想性质 巧解题

江苏省如东县洋口镇初级中学801801班 缪欣晨

有一道需要运用平行四边形性质解决的题目，条件虽然不多，但是却让我费了不少脑筋.

如图1，在△ABC中，AB=AC，点D为边BC上的一点，以AB、BD为邻边作平行四边形ABDE，连接AD、EC，求证：AD=EC.

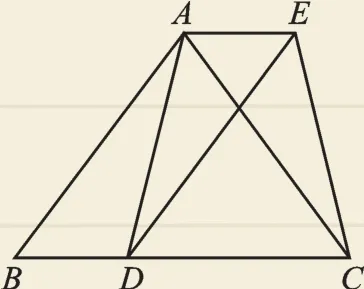
图1

初读题目感觉无从下手，就只能根据已知条件看看能推出哪些结论了，从而再逐步理清证明的思路：由条件AB=AC，而AB是平行四边形ABDE的一边，联想平行四边形的对边相等，可得AB=DE，所以DE=AC.题目要证AD=EC，结合公共边DC，本题就需要证△ADC≌△ECD.

此时根据全等三角形的判定方法可以再证AC、CD的夹角与ED、DC的夹角相等，即∠ACD=∠EDC.

由AB=AC可知∠B=∠ACB，联想到平行四边形的对边平行，有AB∥DE，可得∠B=∠EDC，进而有∠ACB=∠EDC，问题得证.

证明过程略.

反思：由题目的已知条件联想到平行四边形的相关性质，尽可能得出有关的结论就能找到证明问题的思路.平行四边形的对边平行且相等看似不起眼，但若忽视它们，就会在解题过程中给我们带来麻烦哦.

教师点评：同学们在小学阶段就已经学习过平行四边形，对其有一定的直观认识，相信本文的小作者也不例外.但解本题的过程并没有想象中那么顺畅，初中阶段对学习平行四边形的要求会更高，它需要同学们学会说理以及运用知识进行推理.小缪同学在最初无法找到证明问题的方向时，通过读条件联想相关性质逐渐得到解决问题的办法.我相信这对其他同学也有一定的启发.