车身结构件轴向压溃性能的截面优化

刘博 高云凯 左文杰 李亦文

（1.同济大学，上海 201804；2.一汽解放汽车有限公司，长春 130011；3.吉林大学，长春 130025）

1 前言

车辆发生正面碰撞时，前纵梁结构在缓冲吸能方面发挥着重要作用。碰撞能量的耗散和传递受其轴向变形模式及溃缩特性的直接影响。在车身总体尺寸确定的情况下，前纵梁长度也基本确定，但其截面的几何形状仍具有较大的设计空间。在各种溃缩模式中，轴向逐级压溃能够保持稳定且使吸能效果最大化。因此，在进行冲击载荷传递路径设计及整车碰撞能量管理时，提升前纵梁在轴向压溃过程中的吸能特性是关键环节[1-2]。

前纵梁截面设计中，要考虑材料的成型性等工艺特性。冲压焊接和挤压成型是现阶段主流的成型方式。其中，挤压成型对材料的塑性有较高要求，目前以铝材料应用为主，其密度较小且结构相对简单[3]，可取消相邻部件间的焊接关系，减少零件数量并简化工序，缺点是成本较钢材略高，目前主要应用于高档车或新能源车。现阶段应用最为普遍的承载结构连接工艺是冲压焊接，一般乘用车的前纵梁基本均采用冲压件焊接连接（包括激光拼焊）[4]的形式。这种结构形式成本较低，但截面形状相对复杂，耐撞性能对截面几何参数比较敏感，所以在设计中需要优化截面的几何参数来提高耐撞性[5-6]。

本文以截面关键几何参数作为设计变量，分别建立最大碰撞力标定模型、吸能量标定模型及性能改进的优化数学模型，利用LS-DYNA实现了对不同性能目标等的求解。借助罚函数法将约束条件施加到目标函数，得出遗传算法适应度的评价指标，据此对截面的几何设计变量进行选择、交叉、变异和精英保留操作，有效避免最优个体被破坏的同时保证每次迭代得出的均为改进的解。经验证，本文提出的方法可将前纵梁的碰撞压溃性能优化过程从单纯面向性能转变为面向几何与性能参数的协同层面，有助于防护部件的耐撞性能正向开发。

2 前纵梁轴向压溃性能优化数学模型

前纵梁前端结构截面复杂，其几何形状可简化为若干个几何硬点，将每个硬点的坐标(xi,yi)作为变量来控制截面的形状。因某些特定设计要求和布置上的约束，某些硬点位置不可调整，另外，拔模角度需满足薄板冲压工艺的特性，板料间不能相交或干涉，如图1所示。

图1 前纵梁前端直梁优化设计示意

2.1 性能改进优化模型

模型的数学表达式为：

式中，M(X,Y)为前纵梁的质量；li为前纵梁截面第i个边的长度；t为前纵梁板材的厚度，其通常为离散变量；nT为板料离散厚度的总数；Lbeam为前纵梁的轴向长度；ρ为材料密度；n为围成截面的边的数量；Fmax和分别为峰值碰撞力及其设计上限；和Eab分别为前纵梁吸能量的设计下限与实际吸能量；αi为第i个拔模角；nda为拔模角的数量；nisp为交叉点的总数；X、Y为硬点的设计变量，即坐标；和分别为X、Y的下限和上限。

此模型不仅使优化后的碰撞峰值力Fmax不大于指定值，同时使优化后的吸能量Eab不小于指定吸能量，并尽量减小薄壁梁质量。相对原有设计结构，能够显著提高结构的耐撞性，且显著减小整体质量。

2.2 碰撞力标定模型

控制吸能结构在碰撞过程中的峰值碰撞力有利于优化载荷传递路径，并减少与它相连接部件的损失[7-8]。在薄壁管件压溃的动态过程中，碰撞力与时间为高度非线性函数关系，并呈现振动衰减的波形。如直接对如此复杂的碰撞力波形曲线进行标定，会使优化模型的复杂度大幅增加。此外，在碰撞力的时间历程曲线中，第1个峰值力很大，后续的力则较为平缓，即可近似以3段直线来简化复杂的碰撞力。如图2所示，用Fmax和Fmean来描述该曲线。

图2 碰撞力简化示意

如果以对标结构的碰撞力曲线作为性能目标，就要保证碰撞力标定的目标函数，即Fmax、Fmean分别与其对标值的残差尽量最小，即为碰撞力标定的优化数学模型：

2.3 吸能量标定模型

车辆发生正面碰撞时，如果车辆质量Mlpd和碰撞速度v已知，那么碰撞初始总动能为：

在车体耐撞性能开发前期，需要定义传递路径上关键部件的吸能水平，尤其是前纵梁前端平直的部分。通常，设定总动能吸收比系数为λ，即吸能比例。碰撞结束后以前纵梁吸收的能量Eab与总动能的减少量之间的残差作为目标函数，并使残差最小化，达到对总体吸能水平的设计标定。最优化数学模型为：

3 罚函数法处理约束条件

在计算方面，遗传算法的优化搜索方法不依赖于梯度信息，只需要定义搜索方向的目标和适应度函数即可，适用于机械设计、组合优化及软件工程等领域[9-10]。因此，可以使用遗传算法来求解上述3种优化问题。它们都具有约束条件，所以需使用罚函数法来处理约束条件，将约束条件累加到目标函数上，并使用遗传算法的适应度函数来评价该目标函数。

3.1 性能改进优化模型

性能改进优化模型的最大碰撞力的罚函数为：

式中，为最大碰撞力罚系数，根据不同的工程需求，其数值可以不同。

吸能量的罚函数为：

式中，为吸能量的罚系数。

对于拔模角的约束条件也可以得到类似的表达式：

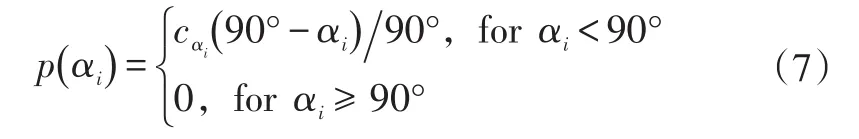
式中，为拔模角的罚系数。

交叉点的罚函数为：

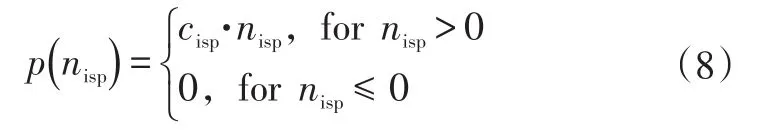
式中，cisp为交叉点的罚系数。

截面优化的遗传算法的适应度函数可以定义为：

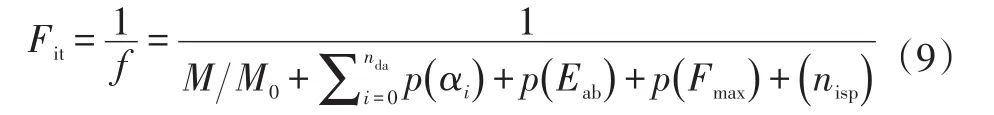
其中，目标函数M被初始质量M0规范化。当获得最优解时，一定有M/M0＜1、p(Fmax)=0、p(Eab)=0、p(αi)=0、p(nisp)=0，故Fit＞1。

3.2 碰撞力标定模型

碰撞力标定模型吸能性、拔模角和交叉点的约束条件的罚函数与模型改进中对应的罚函数相同。于是，碰撞力标定模型的遗传算法适应度函数定义为：

在优化模型中，Fmax与的大小、Fmean与的大小关系是不确定的。所以，在得到最优解时不一定满足Fit＞1，可根据适应度变化判断解是否得到了改进。最后一代的最优个体就是该模型的最优解。

3.3 吸能量标定模型

吸能量标定模型的拔模角、最大碰撞力和交叉点的约束条件的罚函数与碰撞力标定模型中相应的罚函数相同，吸能量标定模型的遗传算法适应度函数为：

其中，被初始总动能规范化。因此，当获得最优解时，一定有，由式（11）得到f＜1，因此，获得最优解的必要条件是Fit＞1。

4 算例分析

基于VB.Net开发了面向耐撞性能的截面几何参数优化求解器，将前文的理论方法进行模块化，方便性能开发设计师使用。它的求解模型输出格式是.K文件，方便利用LS-DYNA求解器进行耐撞性能仿真。优化求解器的主要功能包括：

a.复杂截面薄壁梁的分析和优化。利用该模块的绘图功能，使用者可根据设计方案绘制出各种复杂的截面，可对每一种截面形状进行前处理和求解分析，也能够根据使用者的需求优化截面形状；

b.规则截面的分析和优化。规则的截面形状并不复杂并且结构统一，使用者只需输入与截面的形状相对应的参数和其它属性即可对其求解和分析，依据自己的需求优化出某一形状的截面参数。该模块主要功能设定界面如图3所示。

图3 性能改进的优化求解模块界面

可以利用LS-DYNA求解器对3种优化模型进行耐撞性能仿真，以此来检验优化模型和策略是否有效。

4.1 性能改进优化模型

薄壁板件的厚度和9个可移动的节点坐标（见图4）是复杂截面的设计变量。其中，可移动节点可以在方框区域内移动。在截面的左、右两端均施加焊点，因此焊点区域对称节点的自由度为全约束。优化的目标是适当地减轻结构质量，并控制最大的峰值碰撞力，以此来提高吸能性能。设置界面如图5所示。

图4 可移动节点及其优化区域

图5 性能改进的优化求解模块界面

优化前、后的可移动节点坐标值见图5，最优解出现在变量的设计区间内。质量、性能目标参数、适应度函数的优化迭代均在10步内收敛，并获得了最优解，如图6所示。整个优化过程厚度始终是1.5 mm，优化前、后的最大碰撞力和吸能量均在控制范围内。其中，最大碰撞力下降1.27%，而吸能量增加3.71%，符合设定的约束条件。如表1所示，优化结果质量减少了5.15%，达到了提升耐撞性能的同时实现轻量化的目的。

图6 性能改进模型的各优化参数迭代历程

表1 性能改进模型的优化结果

4.2 碰撞力标定模型

将9个可移动点坐标变化区间设定在原始坐标±10 mm范围内，如图4所示，另有2个厚度变量，共11个设计变量。优化后各截面节点均未超出设定的范围，截面形状变化不大。其关键参数的优化迭代过程如图7所示。

如表2所示，根据各约束条件优化前、后的变化量，可见优化结果较为理想。在厚度不发生变化的情况下，平均碰撞力差异很小，峰值碰撞力差异略大。但是在约束条件下，得到了较低的优化结果，并且吸能量增加较为明显，因此认为标定效果较为理想。

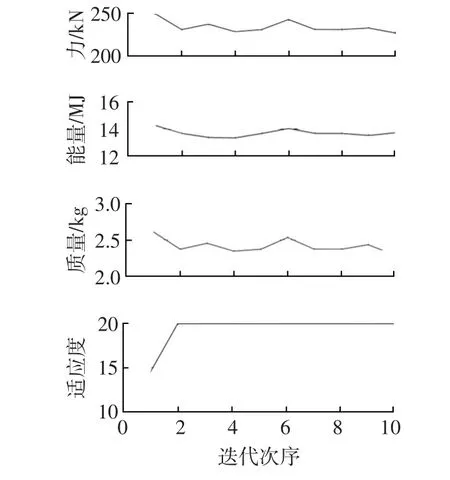
图7 碰撞力标定模型的各优化参数迭代历程

表2 碰撞力标定模型的优化结果

4.3 吸能量标定模型

吸能量标定模型的设计变量与碰撞力标定模型相同，通过设定吸能比例，即希望通过提升吸能水平得到新的结构方案。优化后截面符合约束条件，且与之前的形状相比，变化幅度很小。关键参数的优化迭代的历程如图8所示，且厚度未发生变化。优化后最大碰撞力同样没有超出约束范围，且吸能量显著提高，如表3所示。

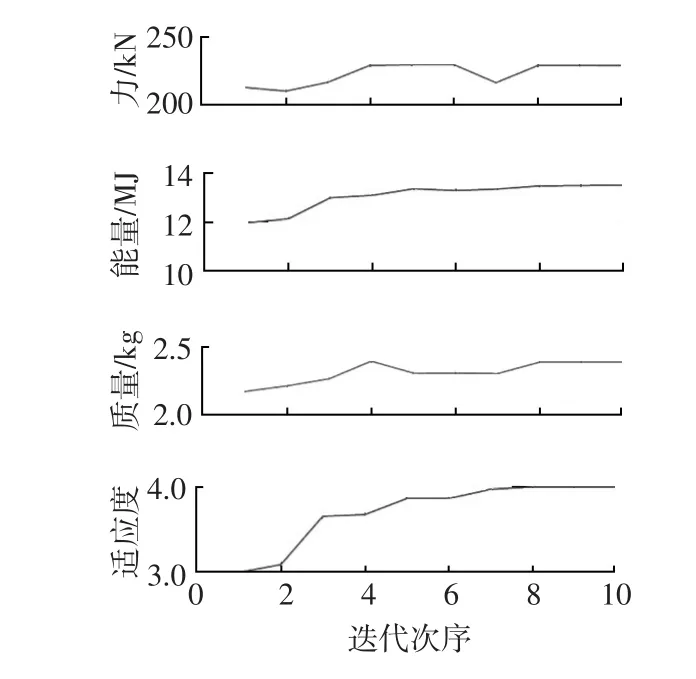
图8 碰撞力标定模型的各优化参数迭代历程

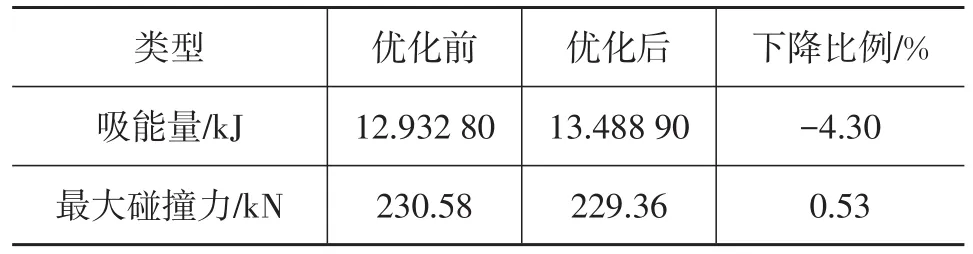
表3 吸能量标定模型的优化结果

5 结束语

本文分别建立了吸能量、碰撞力标定模型和碰撞性能改进模型，用于不同的薄壁梁结构轴向压溃特性优化问题，提供了全面的截面几何参数和力学特性综合优化方案。利用遗传算法对3种优化模型进行求解，并利用LS-DYNA求解器进行碰撞仿真分析。数值算例验证了优化模型的合理性，论证了所开发的集成优化求解器的流程，能够有效地对车身吸能部件进行耐撞性能提高的正向设计。

参考文献

[1]Peroni L,Avalle M,Belingardi G.Experimental investigation of the energy absorption capability of continuous joined crash boxes[C],Proceedings of the Twentieth International Technical Conference on Enhanced Safety of Vehicles.Lyon,France,2007.

[2]Qi C,Ma Z D,Kikuchi N,et al.Fundamental studies on crashworthiness design with uncertainties in the system[J].SAE Technical Paper,2005,2005-01-0613.

[3]Sujeet K,Moqtik A,Saraf M.Lightweight materials and their automotive applications[J].SAE Technical Paper,2014,2014-28-0025.

[4]宋燕利,华林.车身覆盖件拼焊板冲压成形技术的研究现状及发展趋势[J].中国机械工程,2011，22（1）：111-118.

[5]Zimmer H,Prabhuwaingankar M.Implicitly parametric crash and NVH analysis models in the vehicle concept design phase[C],Proceedings of the Fourth LS-LS-DYNA Anwenderforum.Stuttgart,Germany,2005.

[6]Zimmer H,Umlauf U,Thompson J,et al.Use of SFE CONCEPT in developing FEA models without CAD[C].International Body Engineering Conference&Exposition,Detroit,USA,2000.

[7]龙述尧,陈仙燕,李青.矩形截面锥形薄壁管关于能量吸收和初始碰撞力峰值的优化[J].工程力学,2007,24(11):70-75.

[8]汤春球,袁友利,莫易敏,王峰,吕俊成.基于拉丁超立方抽样的薄壁梁抗弯性能研究[J].汽车技术,2017,12(5):30-35.

[9]Abedi M,Niknejad A,Liaghat G,et al.Theoretical and experimental study on empty and foam-filled columns with square and rectangular cross section under axial compression[J].International Journal of Mechanical Sciences,2012,65(1):134-146.

[10]Zuo W J.An object-oriented graphics interface design and optimization software for cross- sectionalshape of automobile body[J].Advances in Engineering Software,2013,64:1-10.