基于动力悬置优化的商用车转向盘怠速抖动控制研究＊

何水龙 许恩永 韦永尤 蒋占四

（1.桂林电子科技大学，桂林 541004；2.东风柳州汽车有限公司，柳州 545005）

1 前言

发动机是汽车怠速抖动的唯一振源，其振动经由悬置系统传递给车架或车身，并最终通过转向盘、驾驶室地板和座椅传到驾驶员或乘员身上，直接影响驾驶员和乘员的舒适性[1-3]。目前，商用车一般采用大功率柴油发动机作为动力源，其怠速转速低、振动大，如果传递路径隔振差或各子系统固有频率与发动机激振频率接近，将导致转向盘抖动、后视镜抖动、前保险杠抖动、踏板抖动和驾驶室抖动等一系列子系统的怠速抖动问题，严重影响车辆的舒适性和安全性[4-5]。

本文针对某型商用车（改动空间受限）转向盘怠速抖动问题，从隔振理论出发，研究发动机悬置系统优化方法，建立了悬置优化模型，并基于粒子群优化算法获得最优悬置刚度。刚度优化后悬置各阶固有频率分布更合理，降低了振动传递率，有效解决了该车转向盘怠速抖动剧烈的问题，提高了整车舒适性。

2 发动机悬置隔振原理

2.1 悬置系统隔振率计算

发动机悬置系统是动力总成和车架之间的衔接部分，起支承和隔振作用，用于减小并控制发动机振动的传递[6]。振动传递系数TA是进行发动机悬置系统隔振设计的重要参数之一[7]，其值常用响应侧力与激励侧力的幅值之比表示，即

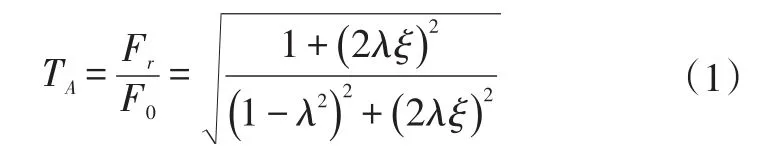
式中，Fr为经悬置传递到车架上力的幅值；F0为发动机激振力幅值；λ为发动机激振频率与系统固有频率之比；ξ为阻尼比。

显然振动传递率越小，隔振效果越好，传递到车架的振动就越小。也有文献采用隔振率G来描述，隔振率G与传递率TA的关系为G=（1-TA）×100%，其值越大，隔振效果越好。

2.2 悬置系统隔振效率分析

通过对商用车发动机悬置系统橡胶软垫测试，得到其阻尼比ξ为0.08，代入式（1）可得传递系数、隔振率及频率比的关系曲线，如图1所示。

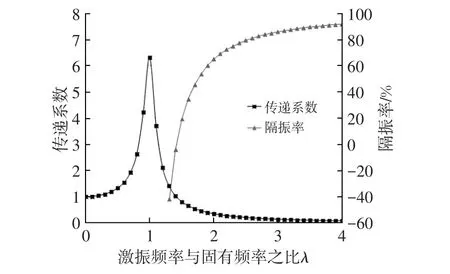
图1 传递率、隔振率及频率比关系曲线

由图1可看出，发动机激振频率与系统固有频率之比λ越大，隔振率G越大，隔振效果越好。在悬置系统设计中，当发动机选定后，其激振频率将无法改变，此时要获得较高的隔振率，则必需降低悬置系统固有频率以提高λ值。在商用车悬置设计中，λ值一般取1.5～3，这是因为λ达到一定数值后，隔振率上升不明显，另外，随着λ的提高，橡胶悬置软垫刚度也会降低，软垫的变形量增大，容易引起动力总成与其它零部件的干涉，降低软垫寿命。同时悬置频率降低易受到来自道路的低频激振力干扰而引起共振，进而影响整车的乘坐舒适性。

3 悬置系统动力学模型

因发动机悬置系统橡胶软垫固有频率远低于动力总成最低阶弹性模态频率，故建模时将其忽略，仅考虑刚体振动模态。同时，由于橡胶悬置结构阻尼只降低系统共振峰值，对固有频率影响较小，因此可将系统简化为无阻尼自由振动系统，发动机悬置系统的固有振动特性可表示为[8]：

式中，M为质量矩阵；K为刚度矩阵；q为质心位移列向量；q″为质心加速度列向量。

当测得动力总成的总质量、质心位置、转动惯量、惯性积以及各悬置3个方向的刚度后，可求得发动机悬置系统的质量矩阵M和刚度矩阵K，进而通过特征值法获得悬置系统的固有频率。

4 悬置系统解耦分析

通常发动机悬置系统的6个自由度方向的振动是互相耦合的，且耦合度越大、振动频率范围越宽，越不利于避开激振力频率，极易引起共振。目前大多基于能量角度评价系统解耦程度，即系统第j阶模态振动对应的第k个广义坐标分配的能量占系统总能量的百分比[9-10]：

式中，j=1，2，3…，6；k为[ ]x，y，z，α，β，γ6 个自由度广义坐标；DIPkj为在第k个广义坐标上发动机悬置系统的解耦率；为振型ϕi的第l和第k个元素；mkl为质量矩阵M的第k行第l列元素。

根据式（4）可确定悬置系统和各阶模态能量解耦度。当DIPkj=100%时，系统在该频率下完全解耦，因此，设计过程中为达到更好的隔振效果，应尽可能提高悬置系统的解耦率，从而获得更好的悬置系统特性。

5 发动机悬置系统优化建模

5.1 发动机坐标系定义

商用车动力总成质量较大，需要分别测试出发动机（含离合器）和变速器的质量参数，然后再合并成动力总成质量参数[11]。为便于合并动力总成质量参数以及获取各质心位置和规范各悬置位置坐标，因此将发动机坐标系作为悬置系统的整体坐标系[12]，并定义为：以发动机飞轮壳后端面与曲轴的交点为原点坐标，向前（指向风扇端）为+X，向左为+Y，向上为+Z，如图2所示。

图2 发动机坐标系

5.2 悬置刚度优化模型

针对转向盘怠速抖动问题，综合考虑发动机悬置主要振型能量解耦度、Z向振动传递率和悬置系统谐振频率的影响，建立了悬置系统参数优化数学模型：

式中，ω1i、ω2i为能量解耦度和谐振频率的加权系数；TAzi为Z向振动传递率；fi、fi0分别为谐振频率与期望频率；DIPii为第i阶频率对应的能量解耦度。

由于发动机激励力主要集中在垂直方向（Z向）和绕曲轴（X向）旋转方向，因此权重ω1i在这两个方向上的取值与其它4个方向的取值之比为3∶1。同时为了避开来自路面低频和发动机频率影响，权重ω2i在这两个频率的取值与其它频率取值之比为2∶1。

5.3 约束条件

a.约束条件1：隔振理论表明，悬置系统的最大固有频率要小于怠速点火频率的，同时大于来自路面的激励频率（约为2.5 Hz），且相邻频率间隔须尽可能大才能有效避开共振，保持良好的隔振效果[13]。本案例中发动机怠速转速为700 r/min，点火激振频率为23.3 Hz，即悬置系统理论固有频率要小于16.5 Hz。

b.约束条件2：1.5≤λ≤3。

c.约束条件3：根据橡胶材料特性，橡胶悬置元件压剪刚度比值在3～8之间[14]，即悬置Z方向和X方向的刚度比值范围为[3，8]。

d.约束条件4：垂直方向和绕曲轴旋转方向解耦率大于80%，其它方向解耦率大于70%。

6 试验验证

6.1 初始参数

该商用车采用四缸四冲程柴油发动机，原车动力总成质量、质心位置、惯量参数通过三线扭摆测试系统[15]测得，各参数如表1所列。

表1 原车动力总成质量、质心位置和惯量参数

该型商用车发动机前悬置为V型布置，后悬置为水平布置，由于产品已经定型，发动机型号和各悬置安装位置及安装角度难以调整，所以不对悬置安装位置及安装角度进行优化，原车悬置参数相关位置见表2，原车前、后悬置刚度参数见表3。

表2 原车悬置位置参数

根据原车初始数据计算得到悬置系统6阶固有频率和振动耦合能量分布如表4所示。

表4 原车固有频率及解耦率计算结果

由表4可知，悬置系统前5阶固有频率小于点火激振频率的，且最小间隔在0.5 Hz以上，符合约束条件中隔振理论要求，但最高固有频率17.9 Hz＞16.5 Hz，接近发动机激振力频率，容易引起共振，不符合频率分布要求。从能量解耦率角度来看，除Y向和绕Y轴旋转方向的解耦度较好外，其它方向的解耦度都小于80%，且最为关键的Z向和绕X轴旋转方向的解耦度都低于70%，各自由度之间耦合严重，需优化改进。

6.2 优化及结果分析

以悬置刚度数学模型（式（5））最小值为优化目标函数，前、后悬置各方向的静刚度值为设计变量，基于前面约束条件，通过多目标融合粒子群优化方法获取最优值，优化结果如表5所示。

对比表3和表5可知，优化后悬置刚度降低，且后悬刚度变化较大。将优化后的悬置刚度代入悬置系统模型，获得固有频率和能量解耦率，结果见表6。

表5 优化后悬置刚度参数 N/mm

由表6可知，悬置系统固有频率范围为4.2～12.9 Hz，最高频率由17.9 Hz降至12.9 Hz，小于发动机点火激振频率的，有效避开了共振，且各阶频率间隔在1 Hz以上，分布合理。从能量解耦角度来看，除绕Z轴旋转方向的解耦率从77.6%降至75.9%外，其它各向能量解耦率都有极大提高，特别是发动机主要激振力方向（Z向）和绕X旋转方向解耦率由原来的67.4%和68.1%提高到了95.4%和81.2%。优化后悬置系统固有频率和振动耦合度降低，发动机激振频率与隔振系统固有频率之比λ也由原车的1.3提高到1.8，极大提高了其隔振能力。

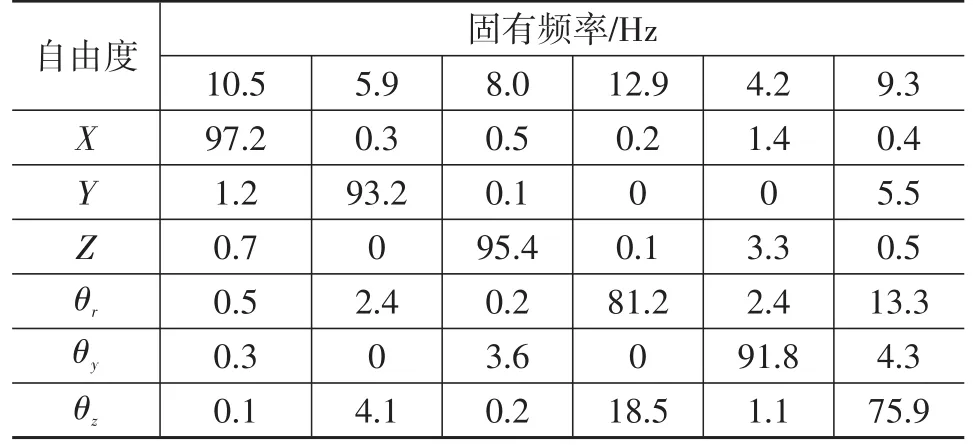
表6 优化后固有频率及解耦率计算结果

6.3 试验验证

根据优化方案，试制发动机悬置软垫总成并装车进行实车测试，获得优化后发动机各缸体支架、悬置支架、驾驶员座椅导轨、转向盘和后视镜3个方向振动加速度值，各项测试指标均优于原车。限于篇幅，文中仅列出与转向盘怠速抖动相关的发动机悬置Z向隔振率和转向盘振动加速度与优化前对比结果，如图3和图4所示。

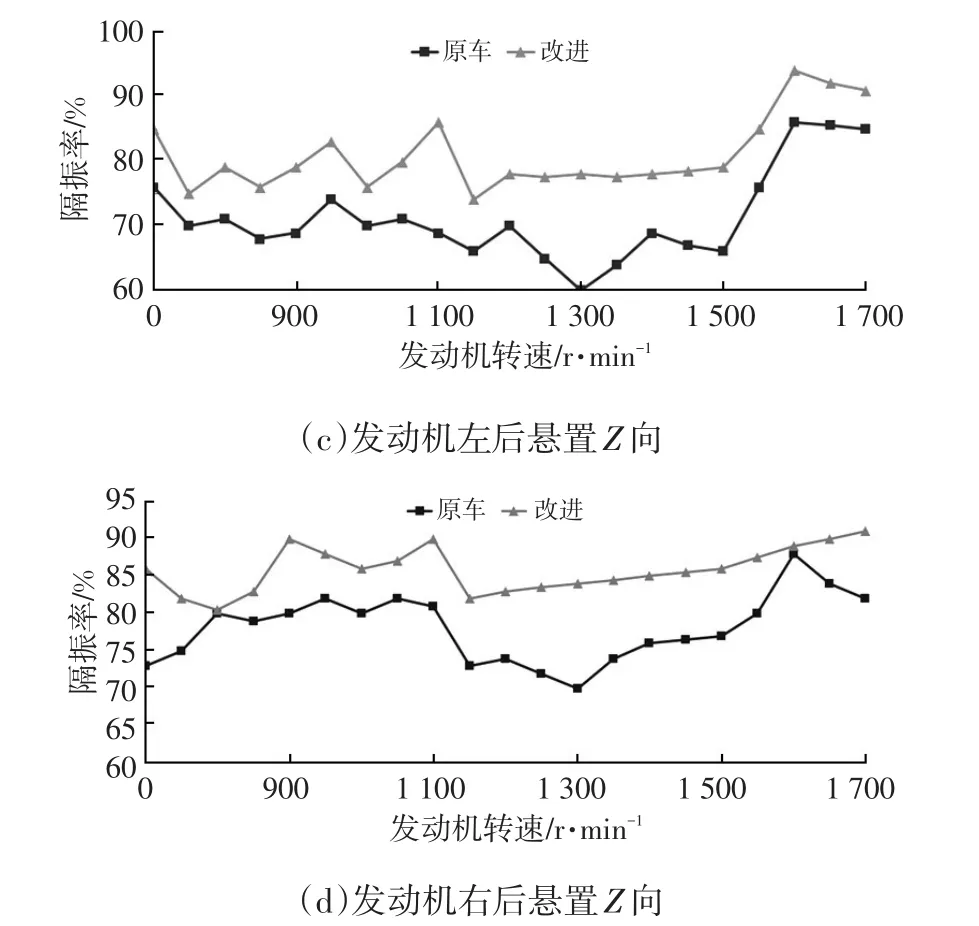
图3 优化前、后隔振率对比

图4 优化前、后振动加速度对比

从图3可看出，优化后发动机左前和右前悬置怠速工况下Z向隔振率从初始隔振率80%和81%提高到了约85%，而左后和右后悬置怠速工况Z向从初始隔振率76%和74%提高到了前悬置优化后的隔振率水平，即85%和86%。由于前悬置初始隔振率较高，隔振效果较好，因此优化后隔振率提升有限，而后悬置初始隔振率较差，优化后提升显著。动力系统悬置优化后实现了悬置系统动态特性与整车动态特性的合理匹配，隔离和吸收了发动机自身振动，有效地控制了发动机干扰力对汽车振动的影响。从图4可看出，实车测试转向盘怠速工况X、Y和Z三个方向振动大幅降低，其中，Z向振动加速度由原来的8.9 m/s2降至0.9 m/s2，振动加速度降幅达90%，有效解决了转向盘怠速抖动剧烈问题，极大地改善了整车的乘坐舒适性。

7 结束语

本文综合发动机悬置主要振型能量解耦度、主要激振方向传递率和悬置系统的谐振频率建立悬置系统优化模型，并基于多目标综合粒子群优化算法实现悬置刚度优化计算，通过产品试制并进行实车测试，结果表明，优化后发动机隔振率在整个转速范围内隔振率明显提升，减轻了汽车发动机向底盘和驾驶室传递振动，有效解决了发动机怠速工况下转向盘怠速抖动问题。

参考文献

[1]王伟,吕吉平,李玉琦,等.某发动机怠速不规则抖动的分析及解决措施[J].汽车技术,2015(4):14-17.

[2]方德广,祖庆华,史文库.轻型客方向盘怠速抖动问题的传递路径分析[J].机械设计与制造,2016(3):61-64.

[3]张志强,徐铁,陈丹华,等.汽车发动机悬置系统多目标设计优化研究[J].噪声与振动控制,2017,37(3):117-121.

[4]辛付龙，钱立军，方驰.电动汽车动力总成悬置系统的多目标稳健优化设计[J].汽车技术,2016,(8):1-6.

[5]Kim S J，Lee S K.Prediction of interior noise by excitation force of the power-train based on hybrid transfer path analy⁃sis.International Journal of Automotive Technology，2008，9(5):577-583.

[6]张兰春,赵清海,张洪信,等.汽车动力总成悬置支架的多目标拓扑优化[J].汽车工程,2017,39(5):551-555.

[7]张健,杨啟梁,胡溧,等.基于ADAMS的12自由度动力总成悬置系统怠速隔振分析[J].汽车技术,2013(1):38-41.

[8]伍建伟,刘夫云,李峤,等.基于遗传算法汽车动力总成悬置系统解耦优化[J].噪声与振动控制,2015,35(5):77-81.

[9]庄伟超,王良模,殷召平,等.基于遗传算法的混合动力汽车动力总成悬置系统的优化设计研究[J].振动与冲击,2015,34(8):209-213.

[10]薛华,刘志强,刘岩,等.基于Matlab的动力总成悬置系统解耦优化[J].噪声与振动控制,2015,35(2):65-68.

[11]郭峰,吕振华,侯之超.动力总成刚体惯性参数的识别方法研究[J].汽车技术,2004(8):15-19.

[12]李骏,张晓艳,付磊,等.汽车低碳化与动力总成技术创新[J].汽车技术,2017(4):1-5.

[13]陈树勋,李志强,韦齐峰.汽车发动机悬置系统的严格解耦与优化设计研究[J].工程力学,2013,30(9):177-183.

[14]李志强.汽车发动机悬置系统动力响应分析与隔振率优化[D].南宁:广西大学,2013.

[15]上官文斌,贺良勇,田子龙,等.汽车动力总成质心与惯性参数测试实验台的开发[J].振动工程学报,2010,23(2):119-125.