基于分数阶无迹粒子滤波的动力电池SOC估计＊

何耀 秦少勋 刘新天 郑昕昕 曾国建

（合肥工业大学，智能制造技术研究院，合肥 230009）

1 前言

动力电池是决定电动汽车性能表现的关键部件之一[1]，准确地估计动力电池的荷电状态（State Of Charge，SOC）能有效地管理电池系统，对动力电池充放电、使用寿命等有着重要的意义[2]。电动汽车以及电池负载系统的实时性与不确定性对SOC估计算法模型提出了巨大挑战[3]。

SOC估计的常见算法有安时积分法（AH integrator，AH）、无迹卡尔曼滤波算法[4]、扩展卡尔曼滤波算法[5]、粒子滤波算法[6]等。目前，更进一层次提高SOC估计精度成为国内外学者钻研的热门问题。文献[7]提出了BPEKF算法，使用BP神经网络的自学习能力和逼近能力，优化和补偿EKF算法的非线性误差，同时降低了等效模型的精度要求。文献[8]提出了基于信息交融的SOC估计算法，该算法根据不同模式切换到适配的模型对SOC进行估计，进一步提升了估计的精度和鲁棒性。文献[9]提出了一种无迹粒子滤波算法，并验证了该算法具有良好的鲁棒性。

滤波算法的准确性在根源上取决于所建立的电池模型能否真实地反映电池特性[10]。典型的电池模型包括电化学模型、等效电路模型[11]、神经网络模型[12]等。动力电池的电化学反应机理模型复杂，难以应用到现有SOC估计中。神经网络模型能够模拟电池的高度非线性特性，但参数训练所需要的样本量较大，在资源紧缺的嵌入式应用中较难实现。常用的等效电路模型一般是整数阶的，近年来，分数阶微积分理论在电池建模中有了初步的应用。文献[13]提出了基于分数阶微积分理论的车用锂离子电池建模及SOC估计方法，该算法准确度高、收敛速度快，是一种可靠的建模方法。文献[14]提出基于分数阶联合卡尔曼滤波的参数估计方法，该方法确定的参数稳定性高。

基于此，本文提出一种基于可变温度的分数阶Thevenin模型的建模方法，采用试验设计（Design Of Experiment，DOE）方法和遗传算法进行参数辨识，通过动态应力测试（Dynamic Stress Test，DST）工况试验证明该模型较传统的整数阶Thevenin模型更加精确，而且适用于温度连续变化的情况。此外，本文采用分数阶无迹粒子滤波（Fractional Unscented Particle Filter，FUPF）算法估计电池SOC并将其与无迹粒子滤波（Unscented Particle Filter，UPF）算法进行比较。

2 动力电池分数阶建模

2.1 电池建模

分数阶微积分在电池建模方面有了初步的应用，文献[15]～文献[17]表明动力电池的本质是分数阶的，而且用分数阶微积分理论建立的动力电池分数阶模型更加精确。

本文根据传统Thevenin模型建立可变温度的分数阶Thevenin模型，如图1所示。其中，Uoc、U0分别为电池开路电压、端电压，Rl、Cl分别为极化内阻、极化电容，二者的端电压为极化电压U1，R为电池的欧姆内阻，UR为欧姆内阻的端电压，I为充、放电电流，n为分数阶阶数。其中R受温度T、SOC和健康状态（State of Health，SOH）的影响。

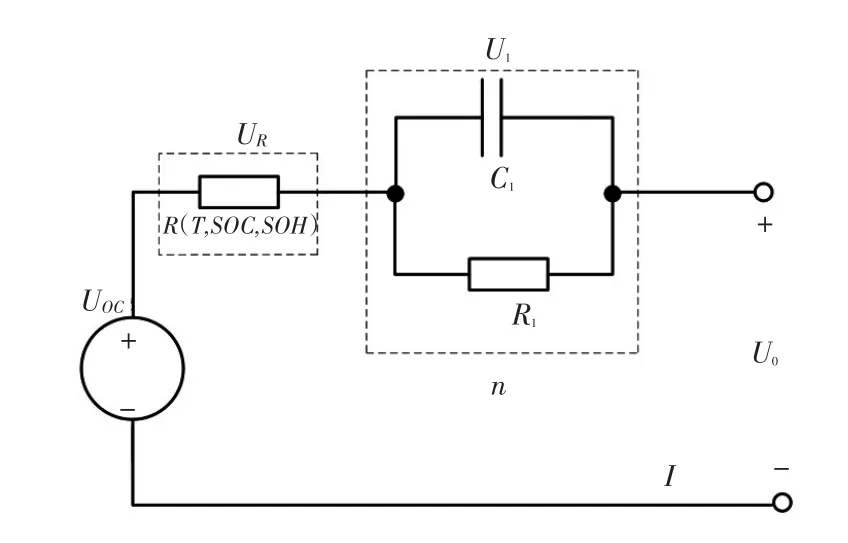
图1 可变温度分数阶Thevenin模型

分数阶微积分的定义式主要有G-L定义、R-L定义和Caputo定义。本文采用G-L定义式：

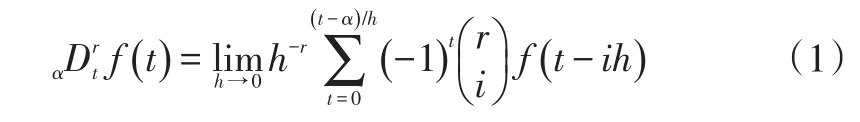
其中

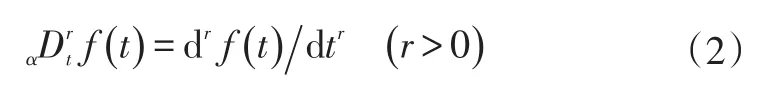
式中，算子表示分数阶微积分运算，α、t分别为积分上、下限；h为步长；i=0,1,2…。

图1中，极化电容Cl可以用分数阶表示为：

式中，n为极化电容的分数阶阶数，n∈R，0≤n≤1。

由图1可建立以下方程：

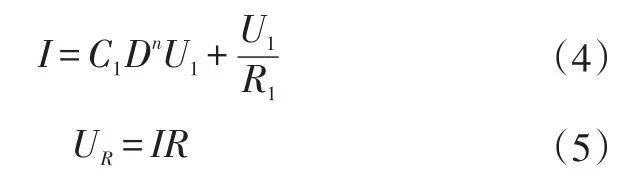
由Nernst模型的常规表达式建立动力电池与来路电压的关系：

式中，k1、k2为模型的辨识参数。

由式（3）～式（6），得到动力电池分数阶模型为：

式中，QN为动力电池额定容量。

由上述关系可得动力电池分数阶模型的状态空间方程为：

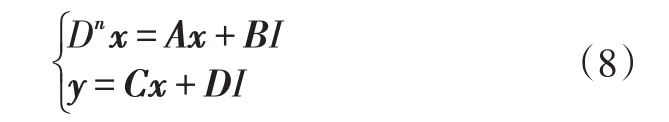
式中，

2.2 电池模型参数辨识

为分析欧姆内阻R与T、SOC和SOH的关系，本文采用DOE[18]方法中的中心复合设计（Central Composite Designs，CCD），此方法设计简单、操作方便。等效模型如图2所示。

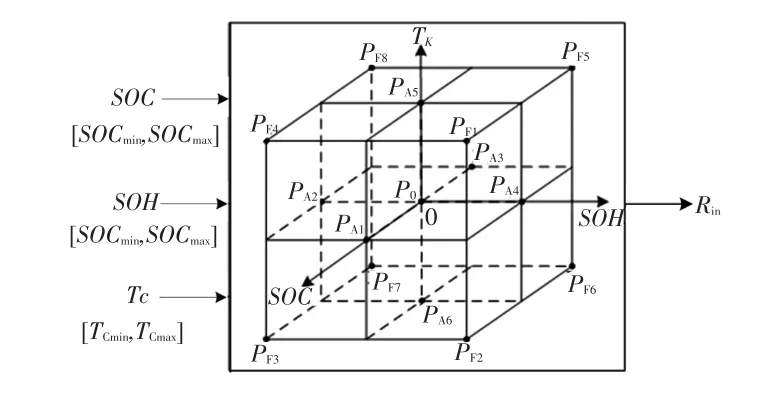
图2 基于CCD的Rin的DOE模型

所建立的模型有3个变量，故采用中心复合中的水平因子方法。拟合的等效内阻模型表达式中包含T、SOC和SOH的1次、2次项、常数项以及交叉项，其表达式为：

其中，Con为常数项；a～i为常系数。

各项系数的拟合值和95%置信水平时的参数置信区间如表1所示。

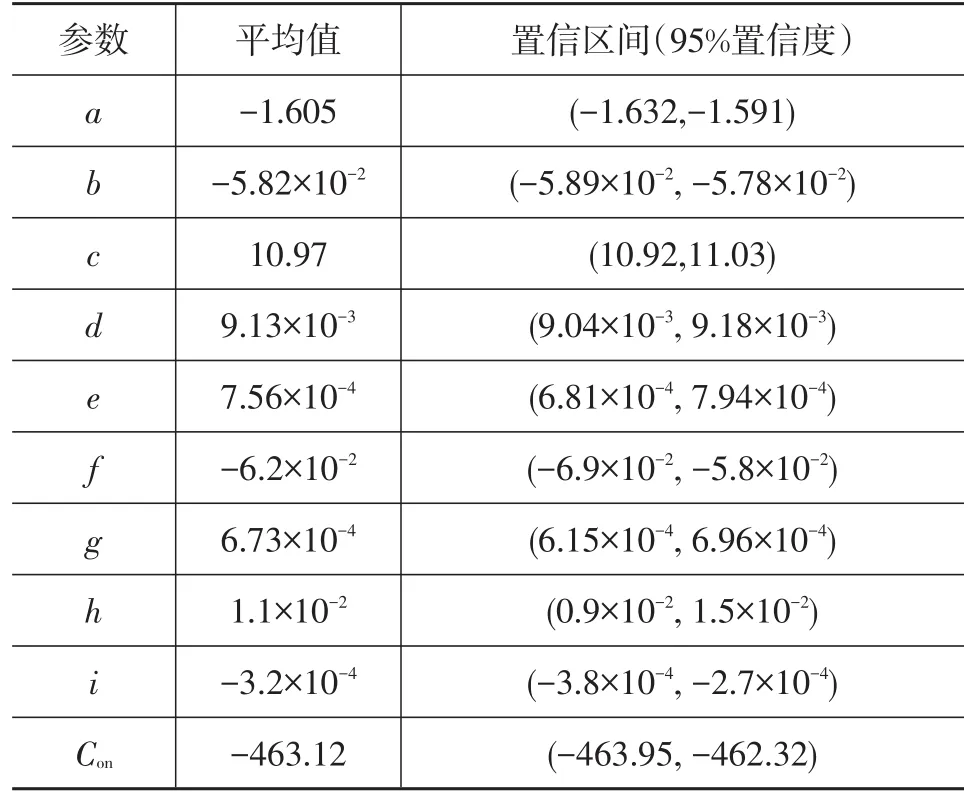
表1 拟合函数各项系数

图3给出了T、SOC和SOH对Rin的独立效果图，其表示各变量在其区间变动时导致总输出变量的变化。

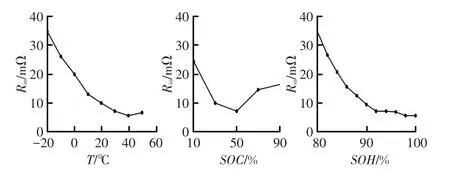
图3 T、SOC和SOH对Rin的独立效应图

由图3可以看出，3个参数对Rin都存在较大的影响，从斜率可以看出，T和SOH对等效内阻的影响较大。表现在表1中，a、c的值较b大。

图4给出了基于所建模型的Rin响应曲面，可以看出，Rin随SOC和SOH的增加而增加，随T的增高而降低，且SOH和T变化对Rin的影响更加明显。

为分析极化电容分数阶的阶数，本文采用遗传算法对阶数n进行参数辨识，遗传算法步骤如图5所示。辨识结果为n=0.87。

3 基于FUPF算法估计SOC

首先将分数阶模型离散化可得：

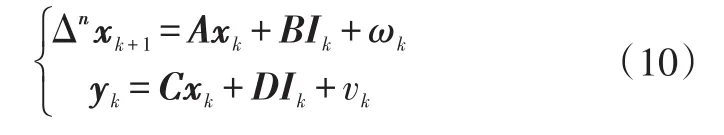
式中，ωk、vk分别为系统状态噪声和量测噪声。

图4 Rin的响应曲面

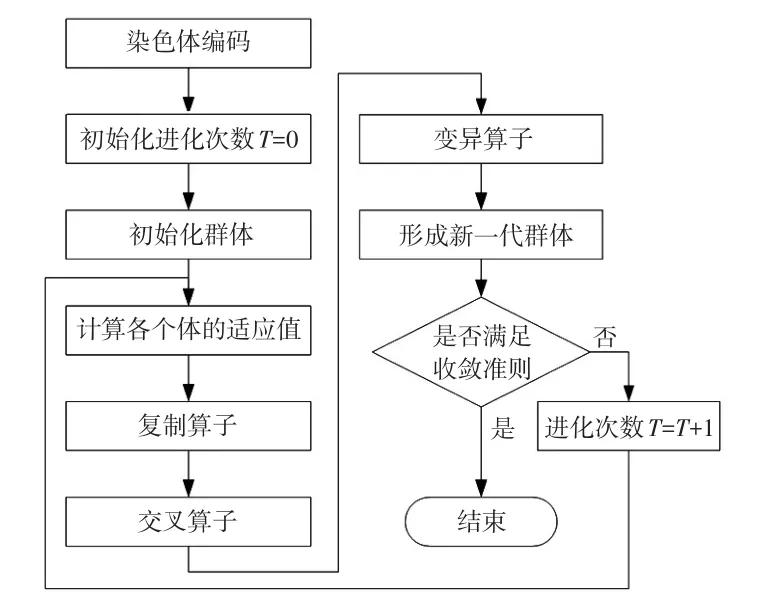
图5 遗传算法流程

根据G-L定义，系统的离散方程可以表示为：

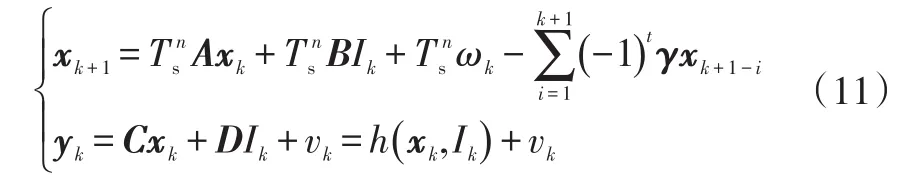
式中，Ts=0.1 s为系统采样时间；；，r为1或n。

根据建立的系统离散方程，采用FUPF算法估计SOC，其步骤为：

a.初始化，利用（0,1）均匀分布生成N个SOC初始值,i=1,2,…,N，可得到N个初始状态粒子和估计误差协方差矩阵：

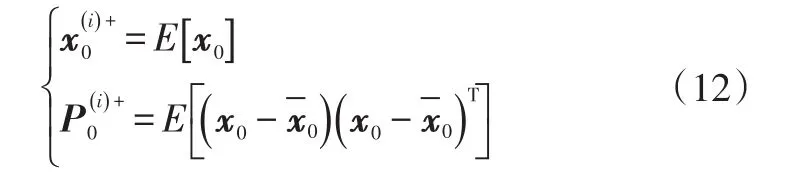
b.对每一个粒子进行Sigma点采样：

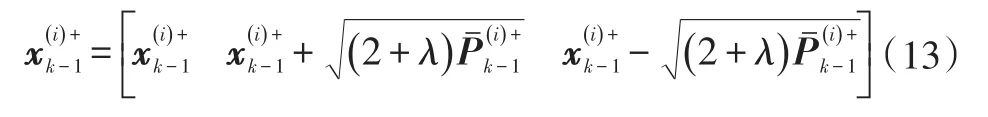
式中，λ为标量参数。

c.引入分数阶对粒子和估计误差协方差进行时间更新：

令表示的第j（j=0,1,…,2n）列列向量，将带入状态方程得到：

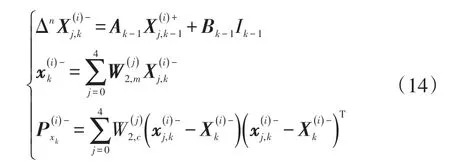
d.粒子量测更新过程为：

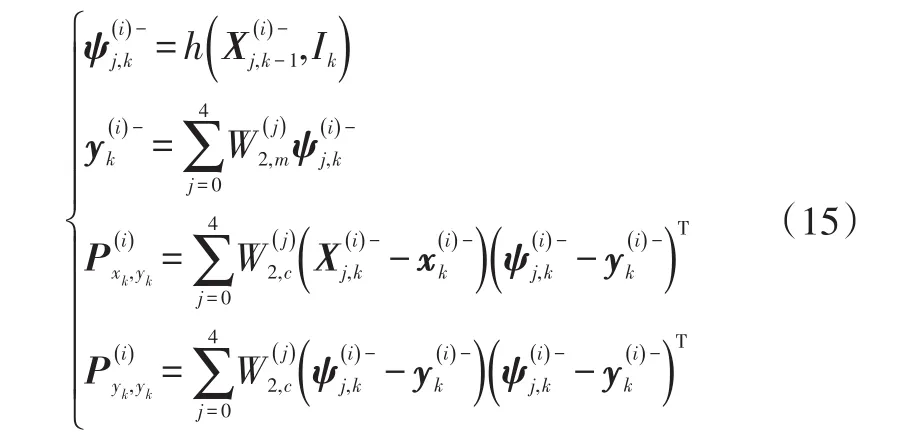
式中，为n=2的无迹变换权重因子。

结合最新测量数据yk对先验估计状态和协方差进行修正：

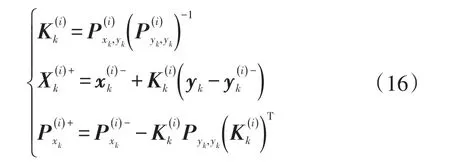
式中，为卡尔曼滤波增益。

e.重采样，由量测结果yk计算粒子的后验概率pi：

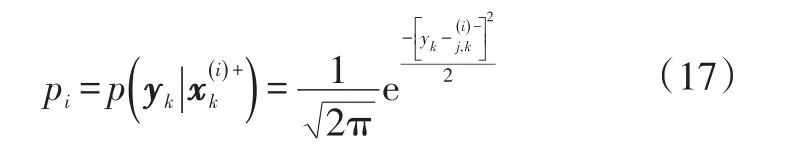
进行归一化后得到：

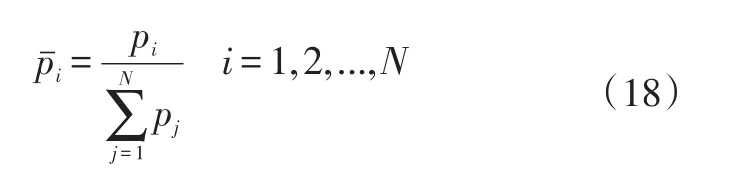
f.更新系统状态：

4 仿真与试验验证

4.1 电池模型验证

为了对可变温度的分数阶Thevenin模型的精度进行验证，选取单节额定容量为9 A·h的磷酸铁锂电池分别在-30℃、-10℃、0℃、10℃、20℃、40℃环境下进行充、放电试验。

为充分验证可变温度的分数阶Thevenin模型具有较高的精度，此处放电波形采用美国先进电池联合会（United States Advanced Battery Consortium，USABC）的《电动汽车电池试验手册》中规定的DST工况波形。经过每个DST工况，电池放出0.45 A·h的电量，20℃时共计20次左右循环可将电池电量放完。将各温度下对锂电池进行充、放电试验结合上述参数辨识结果，在MATLAB中分别对可变温度的分数阶Thevenin模型与传统的Thevenin模型进行仿真，验证电池模型的精确性。图6所示为DST工况电流波形示意。

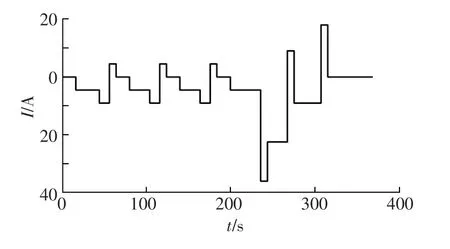
图6 DST工况电流波形示意

图7所示为多个温度下常温与低温DST工况充、放电试验动力电池端电压变化曲线。通过对图7及多个温度下进行DST工况充、放电试验时锂电池的端电压的分析可得：常温下可变温度的分数阶Thevenin模型和传统Thevenin模型参数相差不大、在低温环境下，等效内阻Rin发生变化，会导致传统Thevenin模型的估计误差变大。

表2给出了各温度下两种模型端电压的平均绝对误差。

通过对图7及在多个温度下DST工况充、放电试验电池的端电压变化的分析，结合表2可以看出，利用DOE方法建立的电池模型在DST工况下仍具有精度高、误差小的特点，充分验证了可变温度的分数阶Thevenin模型能够提高电池模型的精确性。

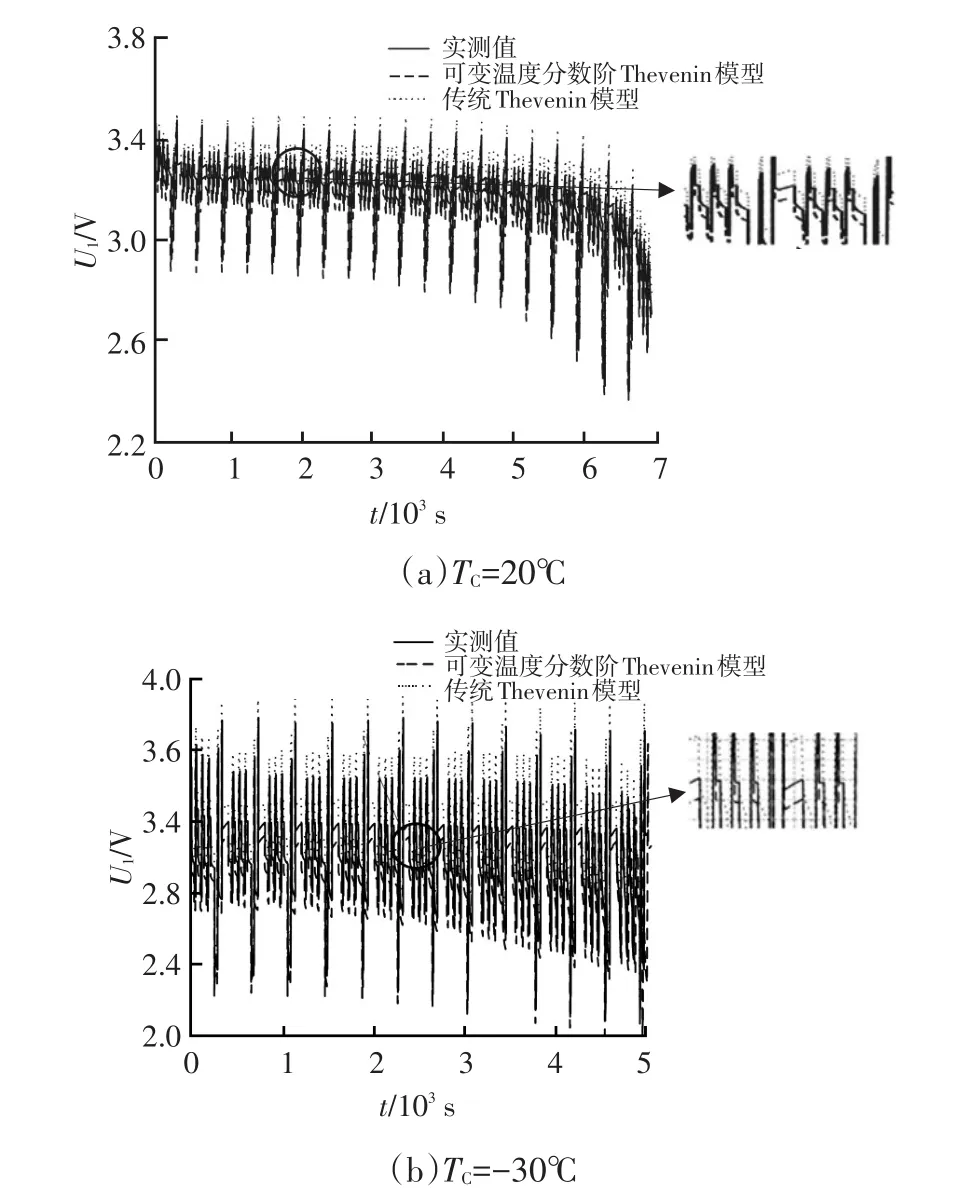
图7 不同温度下端电压曲线

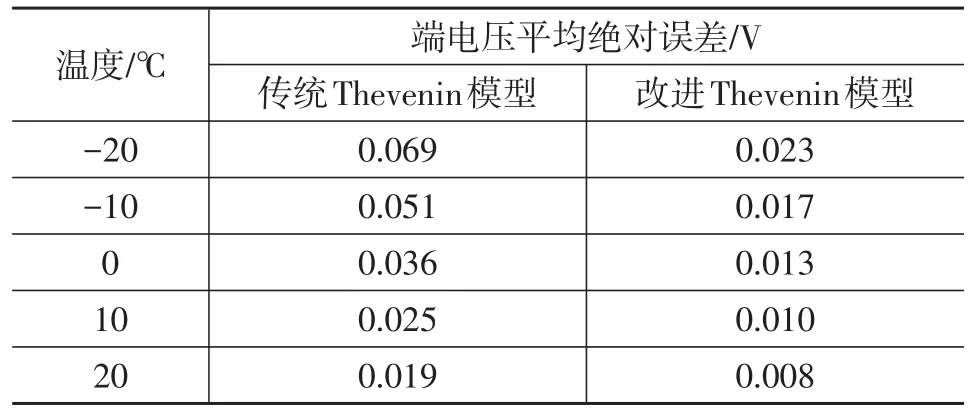
表2 端电压平均绝对误差

4.2 电池SOC估计精度验证

为了验证FUPF算法估计动力电池SOC的精确性，选取单节额定容量为9 A·h的磷酸铁锂电池，进行不同工况的充、放电试验。利用MATLAB/Simulink软件建立动力电池SOC估算模型进行仿真验证，通过与扩展卡尔曼滤波器（Extended Kalman Filter，EKF）和UPF的估算误差进行比较来验证FUPF算法的估计精度。

4.2.1 循环放电试验SOC估计

为了验证FUPF算法在不同温度下的补偿效果，本文分别在-10℃与30℃的环境温度下进行循环放电试验：将SOC=90%的锂电池分3次放电，每次放出30%的电量，每次放电时间间隔3 min。

图8所示为试验电流波形，图9所示为-10℃与30℃下3种算法的SOC估计误差。

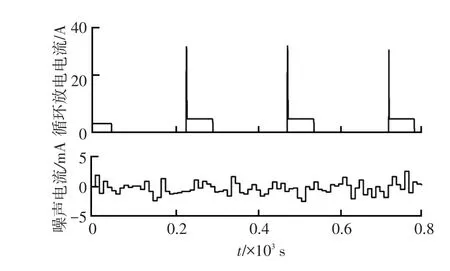
图8 电流波形示意

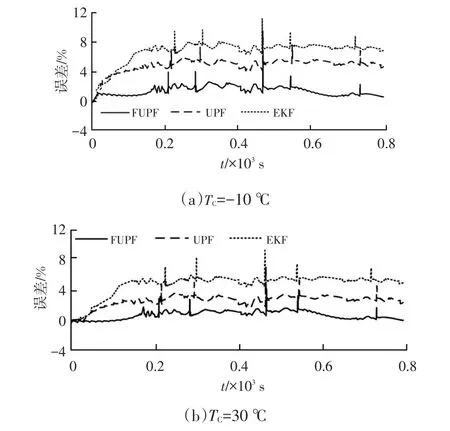
图9 循环放电SOC估计误差

由图9可以看出，在-10℃和30℃条件下，电池模型的修正效果均比较明显。UPF算法的最大估计误差为5.23%，而FUPF算法的最大估计误差为2.16%，性能改善了58.6%。EKF算法的最大估计误差为7.64%。由此可知，分数阶无迹粒子滤波算法估计SOC的精度更高。

4.2.2 US06工况下SOC估计

为验证FUPF算法在实际复杂运行工况中的优越性，本文采用高速公路驾驶时间表US06工况验证SOC算法的精度。使用1个US06循环，历时600 s，为了匹配本文所研究的内容，工况电流按照一定的比例缩小，如图10所示。

图10 US06工况电流示意

图11给出了US06工况的SOC估计误差。与UPF、EKF算法对比，在US06工况下，FUPF算法更接近实际值，准确度更高。

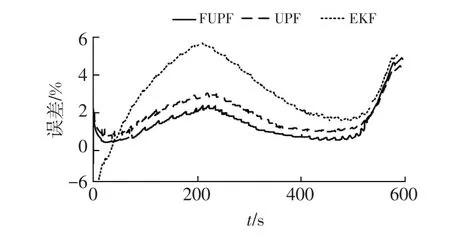
图11 US06工况SOC估计误差

5 结束语

本文在Thevenin模型基础上，融入分数阶理论重新建模，运用DOE方法分析了电池内阻的变化规律，得到可变温度的分数阶Thevenin模型。在此基础上，建立了分数阶无迹粒子滤波算法模型，实现对动力电池SOC的动态估计，所提出的方法具有以下优势：

a.采用DOE方法拟合内阻可以较少的测量数据得到较为精确的内阻模型，在提高效率的同时提高了SOC估算精度；

b.电池模型避免了现有模型在高、低温条件下不适用的缺陷，在环境温度较高或较低时，电池模型的修正效果更为明显；

c.分数阶可变温度Thevenin模型可以更加精确地模拟动力电池。

参考文献

[1]王树坤，黄妙华，刘安康.锂离子电池剩余容量估计与优化分析[J].汽车技术，2017（2）：5-9.

[2]杨世春，麻翠娟.基于PNGV改进模型的SOC估计算法[J].汽车工程，2015，37（5）：582-587.

[3]刘毅，谭国俊，何晓群.优化电池模型的自适应Sigma卡尔曼荷电状态估算[J].电工技术学报，2017，32（2）：108-118.

[4]徐艳民，李剑勇.基于改进无迹卡尔曼滤波是电池SOC估计[J].汽车技术，2018（4）：47-51.

[5]张金龙，佟晖，漆汉宏，等.平方根采样点卡尔曼滤波在磷酸铁锂电池组荷电状态估算中的应用[J].中国电机工程学报，2016，36（22）：6246-6253.

[6]赵又群，周晓凤，刘英杰.基于扩展卡尔曼粒子滤波算法的锂电池SOC估计[J].中国机械工程，2015，26（3）：394-397.

[7]徐艳民.基于BP-EKF算法的电池SOC估计[J].汽车技术，2018（2）：19-23.

[8]何耀，张陈斌，刘兴涛，等.基于信息融合的LiFePO4动力电池组SOC估计[J].控制与决策，2014，29（1）：188-192.

[9]何耀.动力锂电池组状态估计策略及管理系统技术研究[D].合肥：中国科学技术大学，2012：25-35.

[10]Seaman A,Dao T S,Mcphee J.A Survey of Mathematics-Based Equivalent-Circuit and Electrochemical Battery Models for Hybrid and Electric Vehicle Simulation[J].Journal of Power Sources,2014,256(3):410-423.

[11]Nejad S,Gladwin D T,Stone D A.A Systematic Review of Lumped-Parameter Equivalent Circuit Models for Real-Time Estimation of Lithium-Ion Battery States[J].Journal of Power Sources,2016,316:183-196.

[12]商云龙，张承慧，崔纳新.基于模糊神经网络优化扩展卡尔曼滤波的锂离子电池荷电状态估计[J].控制理论与应用，2016，33（2）：212-220.

[13]刘树林，崔纳新，李岩，等.基于分数阶理论的车用锂离子电池建模及荷电状态估计[J].电工技术学报，2017，32（4）：189-195.

[14]李晓宇，朱春波，魏国，等.基于分数阶联合卡尔曼滤波的磷酸铁锂电池简化阻抗谱模型参数在线估计[J].电工技术学报，2016，31（24）：141-149.

[15]Westerlund S,Ekstam L.Capacitor Theory[J].IEEE Transactions on Dielectrics&Electrical Insulation,1994,1(5):826-839.

[16]Macdonald J R.Impedance Spectroscopy[M].California:Society of Photo-Optical Instrumentation Engineers,1981.

[17]Wang B,Li S E,Peng H,et al.Fractional-order Modeling and Parameter Identification for Lithium-ion Batteries[J].Journal of Power Sources,2015,293(20):151-161.

[18]Draheim C,de Crécy F,Hansen S,et al.A Design of Experiment Study of Nanoprecipitation and Nano Spray Drying as Processes to Prepare Plga Nano- and Microparticles with Defined Sizes and Size Distributions[J].Pharmaceutical research,2015:1-16.