地铁曲线段轮轨接触三维有限元分析

王晨阳，赵吉中，徐 祥，阚前华

（西南交通大学力学与工程学院，成都 610031）

引言

地铁已成为城市轨道交通的重要组成部分，具有载客量大、快速、正点、低能耗、少污染、乘坐舒适的优点，享有“绿色通道”的美誉。然而，由于城市规划的原因，地铁线路有很多小曲线半径段，轮轨滚动接触疲劳和磨损在这些区域尤为突出，极大的危害了地铁的安全运行，已经成为地铁线路伤损的主要诱因。

艺体类术课与技能技巧课程：不断加大学生自学自训的任务与要求，以获得核心技能技巧或技能技巧的核心环节在技能技巧形成过程中的迁移能力并进行自学自训为主要目标。

轮轨接触诱发的钢轨伤损一直是国内外学者研究的热点和难点。例如，Olofsso等［1］通过实验调查了钢轨材料的磨损、塑性变形和摩擦特性；Ramanan等［2］对轮轨接触应力进行了研究，认为直接把荷载加在接触点上或轮缘上的方法［3］误差较大；Zhao等［4］的研究发现硬化率对钢轨切向伤损影响最大；文献［5－7］通过研究轴重与温度对钢轨伤损的影响，发现裂纹起始点在钢轨次表面；Bruner等［8］研究了钢轨弯曲应变和轮轨侧向接触力的关系；刘洋等［9］研究了钢轨不同大小剥离掉块损伤对钢轨剥离掉块伤损区域的影响，发现在剥离掉块伤损区域长度为20 mm、深度为4 mm时，钢轨等效塑性应变最大，且伤损区域后侧的值为前侧的3～4倍，但其研究只是局限在二维情况下，未给出接触斑法向接触力的具体形式；肖乾等［10-11］研究了直线线路上摩擦系数和轮轨冲角对高速列车轮轨滚动接触面间蠕滑力和蠕滑率的影响，发现摩擦系数对轮轨接触斑面积和最大接触应力影响非常小；随着摩擦系数增加，旋转中心在接触斑内沿牵引方向前移，轮轨冲角对纵向蠕滑率几乎没有影响，但对横向蠕滑率有较大的影响；该研究只是局限在直线段，未考虑横向力作用［12-13］；王文建等［14］对轮轨损伤行为和钢轨滚动接触疲劳进行了实验研究，分析了轨道参数对轮轨接触斑的影响，并针对钢轨疲劳损伤与磨损提出了预防措施；陆文教等［15］对地铁车轮磨耗对轮轨接触损伤和动力学性能进行了研究；张璘等［16］等对地铁直线段轮对横移量对轮轨磨耗的影响进行了有限元分析，重点讨论了不同横移量下接触斑的变化；黄龙文等［17］建立了铁路曲线段轮轨接触表面应力和内部应力计算的数学模型。

综上所述，已有研究对地铁曲线段轮轨接触行为的研究还不够深入。曲线段钢轨由于超高和离心力的存在，其受力状态比直线段钢轨更为复杂和恶劣。因此，基于已有直线钢轨伤损的研究成果，进一步深入研究曲线段钢轨的各类参数对轮轨接触行为的影响十分必要，可以为地铁运营及维护提供一定的参考，具有重要的工程实际意义。

本文通过有限元软件ANSYS建立了参数化的三维轮轨接触模型，通过改变轮轨接触中行车速度、超高、曲线半径、轴重、轮轨接触位置和摩擦系数等参数，研究了它们对曲线段地铁在行驶过程中最大等效应力的影响。

1 轮轨接触有限元模型

1.1 有限元网格

图5为钢轨最大等效应力随行车速度的变化情况。其中每个数据点代表一个工况，而数据点所对应的纵坐标，即为当前工况钢轨的最大等效应力值。由图5可知，速度变化对钢轨最大等效应力影响显著。当速度区间处在35 km／h～80 km／h时，增大速度会导致钢轨的最大等效应力先减小，在达到最小值后迅速增大。值得注意的是，这种增长趋势并不是线性的，随后最大等效应力随速度增加而增加的趋势会逐渐减缓。

图1 轮轨几何模型

将轮轴节点与车轮中心点耦合，集中力施加在耦合点上。同时，为了增加有限元计算的收敛性，将Fx和Fy分两个载荷步进行施加。为简化起见，不考虑轨枕对钢轨的弹性支撑作用，对钢轨底部施加固定位移约束。

为了获得轮轨接触斑准确的计算结果，对车轮接触中心左右15°范围和钢轨接触中心左右100 mm的长度区域进行了精细网格划分。进行轮轨接触分析之前，首先进行弹性赫兹接触验证，保证有限元分析获得的最大接触应力与解析解之间的误差不超过5%，否则继续优化网格，直到满足误差要求为止。最终，满足上述要求的接触区单元网格尺寸取2 mm，轮轨接触有限元网格如图2所示。

图2 轮轨接触有限元网格

1.2 材料参数

对车轮和钢轨进行现场取样，进行单调拉伸试验，基本材料性能：车轮和钢轨的弹性模量分别为217 GPa和208 GPa，泊松比均为0.3，密度为7900 kg／m3。采用多线性各向同性硬化模型模拟车轮和钢轨的塑性流动特性，在实验曲线上取应力－应变数据点确定多线性各向同性硬化模型的材料参数，取点分布如图3所示。在实验曲线曲率较大的区域，增加取点数提高模拟的精度。

向心力F计算：

图3 车轮与钢轨的实验和模拟的单拉曲线

1.3 载荷和边界条件

列车在通过曲线时，作用在车轮上的载荷除轴重外，还必须考虑由离心力和超高所引起的横向力作用，可通过指向曲线外侧的离心力与车辆自重导致的指向曲线内侧的重力分量之差计算，其受力示意图如图4所示。

图4 曲线段钢轨受力分析示意图

其中，v为列车的行车速度，R为钢轨的曲线半径，m为列车质量。重力G和向心力F沿x和y方向的分量即为横向力Fx和垂向力Fy。

采用有限元软件ANSYS14.5进行三维有限元分析，车轮和钢轨均选取SOLID185实体单元。采用面－面接触模拟车轮与钢轨的接触过程，目标单元和接触单元分别为TARGE170和CONTA173。

企业外宣翻译一方面要客观、真实、准确地反映产品质量特征;另一方面，要跨越目的语与源语之间存在的语言文化差异，运用变通的翻译方法，拉近与目的语读者的心理距离，使他们最大限度地产生对产品的认同感，才能达到积极良好的宣传效果，吸引更多的潜在客户。例4原文中列举了企业获得的许多权威认证来凸显企业的质量优势，是典型的“第一人称视角”，这种做法在西方人看来却有重复自夸的嫌疑，效果可能适得其反。译文取质量、效率和顾客满意度三点，简化翻译，更能实现宣传功能。

开展食葵机械化收获技术研究，有助于进一步提升食用向日葵的机械化收获水平，减轻了农民的体力劳动，将更多地劳动力从土地中解放出来，创造更多地经济价值[2]。

2 钢轨等效应力影响因素分析

2.1 曲线半径对钢轨等效应力的影响

曲线半径主要是描述曲线上某处弯曲变化的程度，是曲线段钢轨特有的一种参数。采用控制变量的方式研究曲线半径对钢轨等效应力的影响，采用表1所示的三组工况，曲线半径分别取250 m、300 m和400 m，其他参数不变（超高为0.096 m，轴重为12 t，摩擦系数为0.1），提交ANSYS进行计算。其中，符号“Δ”表示参数的增量值。

表1 曲线半径和速度变化参数

车轮采用 LM踏面，材料型号为 ER8，钢轨采用60 kg／m轨型，材料型号为U75V。车轮和钢轨的几何模型如图1所示。

图5 曲线半径对钢轨等效应力的影响曲线

进一步比较不同曲线半径下的结果可知，不同曲线半径下的最大等效应力的谷值几乎不变，即曲线半径的改变对钢轨最大等效应力的谷值影响不大。同时，随着曲线半径的降低，最大等效应力的谷值对应的速度随之降低。这意味着随着曲线半径的减小，当行车速度也要减小到合适的值，才能降低钢轨的最大等效应力。

目前来看，我国再生资源回收利用主要品种回收率基本低于60%，与发达国家80%以上的回收率相比仍存在较大差距，再生资源产业产值提升空间较大。2017年再生资源回收量实现2.82亿吨，同比增长10.16%，回收总值达到7551亿元，同比增长27.91%，主要原因是国际期货市场钢铁、有色金属等原料价格持续上升，叠加供给侧改革和去产能等政策推动，再生资源回收实现量价齐升。随着再生资源回收增长缓慢趋势的持续改善，行业将逐步走出效益低迷态势。预测后十三五时期，再生资源回收体系制度将逐步完善，市场化程度也将逐步提高，行业有望延续景气度。

2.2 超高对等效应力的影响

为研究超高对钢轨最大等效应力的影响，选取了超高分别为0.096 m、0.106 m和0.120 m（表2），保持其它参数不变（曲线半径为300 m，轴重为12 t，摩擦系数为0.1），共26个工况进行分析。

表2 超高和速度变化参数

本论文提出运营商融合D P I（D e e p P a c k e t Inspection 深度包检测）采集方案，统一提取现有网络中源数据，通过标准化数据格式，快速为各个政府部门和运营商提供数据。

图6 超高对最大等效应力的影响曲线

2.3 轴重对等效应力的影响

轴重是钢轨承受的全部载荷，其对钢轨等效应力的影响不言而喻。通过改变轴重，其他参数不变，研究轴重对钢轨等效应力的影响。表3列出了研究的三组参数，轴重分别为12 t、15 t和18 t，其他参数不变（曲线半径为300 m，超高为0.12 m，摩擦系数为0.1），共24个工况。

表3 轴重和速度变化参数

图7为钢轨最大等效应力随速度的变化曲线。由图7可知，不论轴重为12 t、15 t或是18 t，钢轨的最大等效应力随速度的变化规律相同。随着速度的增加，最大等效应力先减小，当到达谷值后，速度的继续增大会导致等效应力的增加，但是这种增加的速率会逐渐放缓。不同轴重对应曲线的谷值不同，即轴重对钢轨最大等效应力的谷值影响较为显著，轴重越大，钢轨的最大等效应力越大；同时，最大等效应力谷值随着轴重的增加而增加。在地铁设计中，通常考虑满载状况进行行车速度设计，未考虑轴重变化下行车速度的改变也会导致最大等效应力的降低，这将导致附加磨耗的产生。

将表2中26个工况的计算结果进行汇总，绘制不同超高下钢轨最大等效应力随速度变化曲线（图6）。由图6可知，钢轨最大等效应力先随着速度的增加而减小，在设计速度附近达到谷值，随着速度的增加最大等效应力开始增大，但是这种增加的趋势会逐渐放缓。与曲线半径对最大等效应力的影响类似，超高分别为0.096 m、0.106 m和0.120 m的三条曲线的谷值几乎相同，这表明超高的变化并不会影响钢轨最大等效应力谷值的变化。此外，不同超高下最大等效应力谷值对应的速度不同：超高值越大，最大等效应力谷值对应的速度越大。这是因为，超高越大，重力的水平分量越大，列车的离心力可通过重力的分量进行平衡；当速度逐渐增加时，离心力越来越大，超高引起的重力分量不足以平衡离心力时，必须依靠外轨的挤压来平衡离心力，导致钢轨的最大等效应力急剧增加，随着施加的推移，容易造成外轨在短时间内造成严重磨耗。

图7 轴重对最大等效应力的影响

2.4 接触位置对等效应力的影响

由于小曲线半径处受力复杂，车辆行驶过程中，轮轨接触位置不易保持，车轮和钢轨之间会发生不断的相对移动，如图8所示。当车轮和钢轨之间发生相对移动时，其接触位置发生相应的变化，钢轨的最大等效应力也会发生改变。以钢轨的顶面中心为原点局部建立坐标系，讨论车轮不同横移量下钢轨最大等效应力的影响。

除需要了解钢轨最大等效应力在不同轮轨接触位置的分布规律外，还需要探究其它参数，如曲线半径、超高、轴重和速度是否会进一步对这种分布规律造成影响，具体工况设计见表4。

图8 接触位置坐标系

(1)哈拉湖南部高山区。阴离子之间相关性较低，阳离子之间相关性较高，表明阳离子交换作用较频繁，Cl-与K+，Na+，Ca2+，Mg2+呈显著性相关，原因是受到了白云岩、长石、岩盐的溶解影响。Mg2+与呈显著性相关，考虑是基性岩浆岩的溶解影响，矿化度与呈显著性相关，说明了矿化度主要来源于这几种离子，见表2。

表4 接触位置、曲线半径、轴重和速度变化参数

图9为钢轨接触位置的演化过程。由图9可知，由于钢轨表面是由多段曲面组成，其表面的接触状态较为复杂，接触斑并未呈现出与赫兹弹性接触理论解相符的椭圆形，而是随着接触位置坐标X的增加，接触斑面积呈现出先增大后减小的趋势。

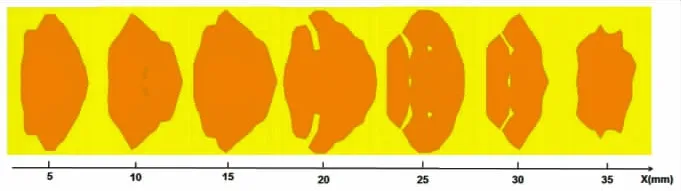
图9 不同接触位置下钢轨顶面接触斑演化云图

图10 为Cp0～Cp4五组工况下钢轨横截面的等效应力分布云图。由图10可知，接触位置的移动，对等效应力的分布影响显著，接触坐标x＝15 mm时，出现了多点接触情形。

图10 不同接触位置下钢轨横截面等效应力分布云图

为了进一步量化最大等效应力随接触位置的变化情况，图11显示了Cp1，Cp2，Cp3和Cp4四组工况下最大等效应力随接触位置的变化曲线。由图11（a）可知，在接触位置处于x轴坐标5 mm～35 mm区间内时，钢轨的最大等效应力先随着x轴坐标的增加而减小，而当x轴坐标减小到某一谷值后，x轴坐标的继续增加会导致钢轨最大等效应力的显著增加。曲线半径的变化不会对这种先减后增的趋势造成影响，但会改变最大等效应力谷值对应的速度。这意味着当列车通过一个曲线半径较小的曲线段钢轨且轮轨接触位置落在远离轮缘的一侧时，钢轨的最大等效应力会出现较小值。同理，如果列车通过的曲线段钢轨的曲线半径较大，轮轨接触位置靠近轮缘一侧时钢轨的最大等效应力会有较小值。

图11 接触位置对等效应力的影响

由图11（b）可知，超高和行车速度的变化对钢轨最大等效应力有显著影响，其值随X轴坐标值的增加先增后减。同时，超高的增加会使最大等效应力的谷值向靠近轮缘的一侧移动，而速度的增加会使最大等效应力的谷值向远离轮缘的一侧移动。

由图11（c）可知，最大等效应力在x＝15 mm附近最小，且轴重的增加会提高谷值，但不会改变谷值出现的位置。而偏移这一位置均会导致最大等效应力的急剧增加。这意味着，不同曲线半径的曲线段地铁在服役过程中，超高过高或过低、速度过高或高低均会引起钢轨接触位置的移动，一旦偏离初始接触位置，最大等效应力均会增加，进而加速滚动接触疲劳失效。

最后,依据节点的HTHS速度,构建下一跳转发节点的候选集C。如果节点的HTHS速度大于SpeedThreshold,则将此节点加入候选集C,如式(8)所示:

通过问卷调查可知，大部分有意向的人群的学习时间集中在下午与晚上。其中，选择下午的一般为学生，比如大学生的在校课程并不是全天都有的且大多数都在上午，因此下午是其集中选择的时间段，且其学习提升普通话的目的一般都是为了后期的大学生活。而选择晚上6点以后的一般都是在职人员。针对上述不同人群及时间选择的集中性，本文认为该培训机构应该选择在晚上设置语言学习初中级班，以提高在职者的汉语水平为最终目的，而下午及部分上午时段可以针对不同学生进行基础性为主的教学。以此满足不同群体的需求。

2.5 摩擦系数对等效应力的影响

地铁曲线段钢轨由于小曲线半径较小，车辆行驶过程中，轮轨接触位置不易保持，服役过程中轮轨表面的平顺度不断被消弱，其摩擦系数也相应的发生变化。为了探究摩擦系数对列车运行时钢轨最大等效应力的影响，图12给出了不同速度下的最大等效应力变化曲线（曲线半径为300 m，轴重为12 t，超高为0.12 m）。由图12可知，不同摩擦系数下最大等效应力随速度变化曲线差异不大，这表明摩擦系数对最大等效应力影响不大。需要说明的是，钢轨的滚动接触疲劳与最大等效应力存在关联；然而，钢轨的磨耗不仅跟接触压力、摩擦系数、蠕滑比有关，还与钢轨表层的硬度有关。

图12 摩擦系数对最大等效应力的影响

3 结论

建立了小曲线半径段地铁轮轨接触三维有限元模型，讨论曲线半径、超高、轴重、接触位置和摩擦系数对等效应力的影响，主要结论有：

“那你试试看把盆拿到床边站上去是不是可以变高？”（欢快地去拿盆，放在了床一米外站上去。）“图图站盆上是变高了，但我们还是爬不上床啊！”（又嗯了一声。）“图图是不是要把盆放到床边试试看呢？”（下来，拿盆，依然放在够不着床的地方。）

（1）曲线半径和超高的改变不会影响钢轨最大等效应力谷值的变化，但轴重的增加会使谷值升高，且钢轨最大等效应力随着轴重的增加而增加。摩擦系数对最大等效应力影响不大。轨道线路设计时，尽量避免线路半径过小，列车应杜绝超载，其会导致轴重增加，对钢轨危害巨大。

（2）行车速度的增加会使钢轨最大等效应力先增加再减小，在到达谷值以后，随着行车速度的增加最大等效应力开始增大，但是这种增加的趋势会逐渐放缓。列车过弯时如果减速过甚，会导致钢轨最大等效应力增加，影响其使用寿命。

（3）接触位置靠近钢轨内侧附近时，钢轨最大等效应力随X轴坐标的增加呈现出先增后减的趋势。曲线半径和超高的增加，或速度的降低，将会导致接触位置为靠近轮缘一侧的工况的钢轨最大等效应力减少，远离轮缘一侧的工况的钢轨最大等效应力增大。

通过上述结论可知，在地铁服役过程中，需要控制行车速度、曲线半径和超高三个关键因素，实现地铁线路的变速通行，即在曲率半径很小处，必须控制行车速度在设计值附近。此外，由于轨道下部结构振动的影响，超高在服役过程中将发生变化，可定期测量超高变化，优化行车速度，这样可以保持轮轨接触区的最大等效应力获得最小值，从而提高抗滚动接触疲劳能力。

参考文献：

[1]OLOFSSON U,TELLISKIVI T.plastic deformation and friction of two rail steels-a full-scale test and a laboratory study[J].Wear,2003,254:80-93.

[2]RAMANAN L,KRISHNA K R.Thermo-mechanical finite element analysis of rail wheel[J].International Journal of Mechanical Sciences,1999,41:487-505.

[3]BOGDANSKI S,OLZAK M,STUPNICKI J.Numerical stress analysis of rail rolling contact fatigue cracks[J].Wear,1996,191(1-2):14-24.

[4]ZHAO B,ZHANG S,LU X,et al.Cyclic tangential loading of a power-law hardening elastic-plastic spherical contact in pre-sliding stage[J].International Journal of Mechanical Sciences,2017,128-129:652-658.

[5]SRIVASTAVA J P,SARKAR P K,MEEALA V R,et al.Rolling Contact Fatigue Life of Rail for Different Slip Conditions[J].Latin American Journal of Solids&Structures,2017,14(12):2243-2264.

[6]SRIVASTAVA J P,KIRAN M V,SARKAR P,et al.Numerical Investigation of Ratchetting Behaviour in Rail Steel under Cyclic Rolling-Sliding Contact[J].Procedia Engineering,2017,173:1130-1137.

[7]MA Y,MARKINE V,MASHAL A A,et al.Modelling verification and influence of operational patterns on tribological behaviour of wheel-rail interaction[J].Tribology International,2017,114:264-281.

[8]BRUNER M,CATENA M,CORTISD,et al.Estimation of the wheel-rail lateral contact force through the analysis of the rail web bending strains[J].Measurement,2017,99:23-35.

[9]刘洋,蒋硕,吴亚平.剥离掉块对轮轨滑动接触热弹塑性的影响[J].交通运输工程学报,2016,16(2):46-55.

[10]肖乾,徐红霞,成棣.不同轮轨冲角下高速轮轨稳态滚动接触的蠕滑特性[J].中国铁道科学,2014,35(1):60-66.

[11]肖乾,王成国,周新建.不同摩擦系数条件下的轮轨滚动接触特性分析[J].中国铁道科学,2011,32(4):66-71.

[12]周素霞,薛蕊,张骞.地铁线路曲线段磨耗状态下轮轨滚动接触有限元分析[J].机械工程学报,2016,52(12):129-135.

[13]陶功权,李霞,温泽峰,等.两种轮轨接触应力算法对比分析[J].工程力学,2013,30(8):229-235.

[14]王文健,刘启跃.轮轨滚动接触疲劳与磨损耦合关系及预防措施[D].成都:西南交通大学,2005.

[15]陆文教,陶功权,王鹏,等.地铁车轮磨耗对轮轨接触特性及动力学性能的影响[J].工程力学,2017,34(8):222-231.

[16]张璘,刘佳欢,张军,等.地铁直线段轮对横移量对轮轨磨耗的影响[J].大连交通大学学报,2017,38(5):11-14.

[17]黄龙文,李正美,安琦.铁路曲线区段轮轨接触应力计算方法[J].华东理工大学学报:自然科学版,2017,43(1):133-142.