块体金属玻璃基复合材料在拉伸荷载下的剪切带演化模拟

刘 杰，张 娟，饶 威

（西南交通大学力学与工程学院，成都 610031）

引言

金属玻璃又称非晶合金，自从1960年Duwez等［1］首次制备出稳定的Au－Si非晶合金之后，金属玻璃得到人们的重视，Chen［2］利用快速冷凝技术首次制备出直径达毫米级以上的金属玻璃试样并将其命名为块体金属玻璃（BMG）。大量研究［3-5］表明，BMG具有高屈服强度、高硬度以及高耐磨性等优秀的力学性能，是极具潜力的工程应用材料。但由于在室温下缺乏相应的硬化机制，BMG在受到无约束的外部载荷（如单轴拉伸、单轴压缩压缩）时，几乎所有的塑性变形都高度集中在一个极其狭窄的区域内，形成一条或多条剪切带，剪切带一旦萌生便迅速扩展，导致整个材料发生灾难性的破坏，以至于BMG在宏观上表现为脆性材料。

从20世纪90年代以来，国内外许多学者围绕BMG的增韧做了很多工作，制备出大量块体金属玻璃基复合材料（BMGCS），并进行了一系列实验研究及理论描述。Qiao等［6］制备了内含枝晶的Ti基BMGCS，在室温下的拉伸应变高达15.5%，体现出极高的拉伸塑性变形能力；Son等［7］在研究发现钨纤维增强的Zr基BMGCS压缩塑性应变可达到2.6%。第二相的引入能够有效地阻挡剪切带快速扩展，使其发生偏折或分叉来提高材料的塑性变形能力，且同时具有高强度和高硬度等优秀性能。Qiao等［8］回顾了块体金属玻璃基复合材料的发展、制备技术以及微结构影响，对材料在不同工况下的变形机理进行了实验和理论探讨，认为进一步研究BMGCS内部微观变形机理是必要的。

在BMG基体中加入陶瓷颗粒或金属颗粒，Choi－Yim和Johnson［9］首次制备出颗粒增强型 BMGCS，该文献提出的复合材料造法已经被证明是简单可靠的。随之，大量的颗粒增强型BMGCS被成功制备并进行了实验及理论研究［8］，但对于其潜在的变形机理和力学特性还有待于进一步研究；尤其是BMGCS作为一种拉压不对称材料［8］，且颗粒的体积分数、大小、强度等都会影响其材料内部剪切带的萌生及演化，进而影响其力学性能。因此，研究BMGCS在拉伸载荷下的变形行为，并进一步分析材料的细观结构对其拉伸载荷下变形行为的影响显得十分有必要。

有限元方法可以有效补充实验研究的不足，是目前科研工作中常用的研究手段。Jiang等［10］利用有限元法模拟了BMGCS在拉伸载荷作用下详细的剪切过程，并讨论了微观结构与材料拉伸塑形能力的关系。Li等［11］利用有限元方法模拟了纤维增强型金属玻璃基复合材料的变形和破坏，重点讨论了剪切带的产生和扩展，分析表明增强纤维能有效地提升材料的塑性变形能力。孙龙港等［12］通过数值模拟研究了BMGCS在压缩载荷作用下的微结构效应及其对材料压缩塑性变形能力的影响，描述了剪切带到微裂纹形成的转变过程。大多数有限元模拟工作中，有的将BMGCS细观构造视为理想对称的，建立简化的单胞模型；有的则用二维的平面模型作为代表性体积单元。

本文利用有限元方法，在商业软件ABAQUS中对颗粒增强型BMGCS在拉伸载荷下剪切带的演化规律进行了模拟分析；通过构建不同微结构特征的三维细观模型，研究了颗粒的体积分数、大小以及屈服强度对BMGCS在拉伸变形行为的影响。

1 有限元模型

1.1 几何模型

基于复合材料内部微观结构，建立合理的有限元几何模型，对于有限元模拟结果的准确与可靠是十分重要的。研究证实，颗粒增强型复合材料的代表性体积单元使用周期性单胞模型是较合理的。Rintoul和Torquato［13］提出随机顺序吸附算法来生成单胞模型中颗粒中心的位置坐标，Segurado和Llorca［14］对随机顺序吸附算法进行了详细的说明，同时指出了其存在的不足并加以修正。通过该方法构建的多颗粒单胞模型，既能够保证颗粒在各个方向上的个数是统计平均的，且几何模型有利于有限元离散化［14］。

图1展示了有限元模拟的单胞模型，图1（a）～图1（f）分别为不同体积分数及不同颗粒大小两组材料结构示意图，材料中所含颗粒的细观结构特征已经在相应的单胞模型下方标明。这里需声明，颗粒半径仅表征大小关系，λ仅为任意常数。

图1 不同微结构特征的BMGCS单胞模型

1.2 本构模型

Spaepen［15］通过进一步扩展自由体积理论，提出了自由体积模型来描述金属玻璃的变形行为。在随后的研究中，大量学者利用该模型及其扩展模型对金属玻璃变形过程中的现象进行了合理的解释，目前该模型已得到了广泛认可。Huang等人［16］利用连续介质力学的基本框架，引入自由体积理论，建立了小变形自由体积模型，该模型可以较好地描述BMG基体在变形过程中，剪切带的萌生和演化过程，其主控方程如下：

总应变ε分为三个部分，分别为弹性应变εe、塑性应变εp和由自由体积演化而产生的非弹性应变：

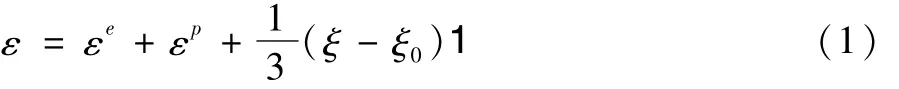
其中：ξ是局部自由体积浓度，ξ0是零应变状态下的自由体积浓度，1是二阶单位张量。由于金属玻璃为各向同性材料，所以弹性应力－应变关系可以由胡克定律给出：

其中：σ是应力张量，μ和k是金属玻璃基体的剪切模量和体积模量。Von－Mises等效剪切应力 τe为：τe＝其中s＝dev（σ）表示偏应力张量。塑性应变率˙εp表示为：

其中是等效塑性应变率。等效塑性应变率的演化方程表示为：

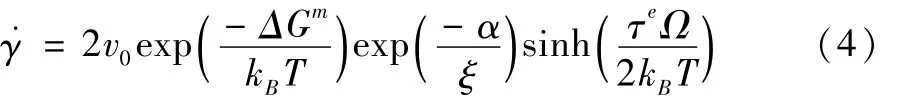
其中：v0表征原子振动频率，ΔGm表征原子活化能，kB是玻尔兹曼常数，T是实验温度，α是几何因子，Ω是原子体积。自由体积浓度的演化方程为：

其中：χ是一个几何参数，v*是一个体积临界值，nD是湮灭一个v*自由体积所需要跃迁的原子的个数。

本文采用Fortran语言将上述本构方程编写成ABAQUS用户子程序，作为BMG的材料模型进行有限元模拟计算。

1.3 周期性边界条件

本文在有限元分析中对单胞模型施加了周期性边界条件。传统的约束条件假设单胞模型在变形过程中表面始终保持为平面，这不仅不符合变形过程中的特点，也对单胞模型过度约束。Xia［17］提出了一种用于周期性代表性体积单元（RVE）边界条件的统一明确的形式，推导出周期性单胞的对立面的位移之差为：

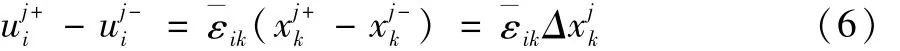
其中：¯εik为平均应变；j＋，j－分别表示沿着 xk的正方向和负方向。由于周期性单胞的对立面始终保持平行，因此Δ在变形过程中始终是一个常数；对于给定的¯εik，即为一个定值，因此可将上式表示：

由式（7）可以看出，周期性单胞对立面上的一组对应点的位移差依然是坐标的函数，故单胞表面不一定一直保持为平面；而且该式不包含未知的周期性部分的位移分量，这使得周期性边界条件在有限元模拟中更加易于实现［18］。

2 结果与讨论

本文的有限元模拟结果首先与文献中的实验结果进行对比，以保证所采用的有限元方法合理准确，进而对不同微结构的BMGCS单胞模型进行单轴拉伸模拟。在有限元分析中，自由体积浓度作为一个内部变量（SDV1），当材料某局部区域的自由体积浓度值高于其周围区域时，表明材料在该区域由于剪切变形导致结构变化，即被用来表征剪切带的萌生及演化区域。本文通过观察自由体积浓度云图，对剪切带的演化规律进行了分析。

2.1 结果对比及剪切带演化规律

文献［19］制备出含钽颗粒的 BMGCS（Zr59.5Cu14.5Ni12.5Al9.8Ta3.7），颗粒体积分数大约为3%，在室温下分别对BMG及其复合材料进行了单轴拉伸试验。其中BMG基体和钽颗粒的材料参数见表1。采用上述有限元模型对文献［19］中的拉伸应力－应变曲线进行模拟，图2展示了有限元模拟结果与实验结果的对比，其中εxx和σxx表示轴向应变和轴向应力。两种结果较好地吻合，证实了本文所采用的有限元模拟方法的可靠性。

表1 BMG基体及钽颗粒的材料参数

图3给出了材料在拉伸变形过程中轴向应变εxx为0.39%、2.99%和4.73%三个时刻的剪切带云图。观察可知，随着拉伸载荷的增大，在基体与颗粒的交界面处垂直于载荷方向上的局部自由体积浓度值最大，剪切带由此处开始萌生，之后剪切带以很快的速度开始扩展。其中图3（b）、（c）中的黑色箭头表示其中一些明显的剪切带，其扩展的方式基本有两种：一种是以大约45°方向朝着基体边界扩展，另一种则是相对位置大致呈45°的相邻两个颗粒之间的剪切带互相接近并融合，融合之后的剪切带开始向周围区域扩展并导致该剪切带逐渐变粗。

图2 数值模拟与实验［19］结果对比

图3 剪切带萌生及扩展过程

值得提出的是，剪切带扩展到一定程度之后，随着载荷继续增大，并没有新的剪切带出现，只是已经生成剪切带区域内的自由体积浓度值不断地增大。由图3（a）到图3（b）是剪切带开始萌生到材料达到屈服时两个时刻的剪切带云图，该过程中剪切带不断扩展并伴随着新剪切带的出现；而由图3（b）到图（c）可以看出，剪切带区域内自由体积浓度在增大但没有出现新的剪切带。

2.2 颗粒体积分数的影响

图4给出了颗粒体积的分数fp为10%、15%、20%三种BMGCS在拉伸变形过程中，轴向应变 εxx达到7.0%时的剪切带云图，其代表性体积单元如图1（a）～图1（c）所示。当颗粒大小不变时，随着颗粒体积分数的增大，颗粒的数目会相应地增多。观察云图可知，较多的颗粒会导致剪切带在更多的区域萌生并扩展，与图4（a）、图4（b）比较，图 4（c）中剪切带数目及分布的区域明显较多，这表明随着颗粒体积分数的增大，材料的局部剪切程度在减小，因此其拉伸塑性变形能力在一定程度上会有所提升。

图4 εxx为7%时颗粒体积分数对剪切带的影响

图5 给出了颗粒体积分数fp分别为0%、10%、15%、20%的BMGCS单轴拉伸载荷下的应力－应变关系曲线。与不含颗粒的BMG比较，随着颗粒体积分数的增大，BMGCS整体的应力－应变响应在降低，材料的弹性模量以及屈服强度都有所降低。这一点相似于常见的复合材料，满足复合材料的混合定律σ＝fpσp＋（1－fp）σM。结合图4中剪切带的分布状态可知，随着BMGCS中颗粒体积分数的增大，剪切带数目增多，材料的局部剪切程度在减小。因此虽然材料的拉伸强度有所降低，但其拉伸塑性变形能力有所提高。

图5 颗粒体积分数对应力－应变曲线的影响

2.3 颗粒大小的影响

图6 展示了颗粒大小分别为r＝0.306λ、0.2λ、0.1λ三种BMGCS在拉伸变形过程中，轴向应变εxx达到7%时的剪切带云图，其代表性体积单元如图1（d）～图1（f）所示。图6（c）中由于颗粒较小，颗粒个数相对的增多能够更加有效地阻碍剪切带的单向扩展，使得剪切带基体中更广泛的区域内萌生并扩展，从而使得BMGCS的拉伸塑性变形能力得到一定的提高。

图6 εxx为7%时颗粒大小对剪切带的影响

图7 展示了上述三种材料在单轴拉伸作用下的应力－应变关系，其中图7（a）是对应力－应变曲线的局部放大，当r＝0.1λ时，BMGCS的屈服强度有所提高，且屈服之后的应力－应变曲线也高于另外两条曲线。总之，随着颗粒半径的减小，材料的弹性模量基本不发生变化，屈服强度及屈服之后的力学响应有所提高。

图7 颗粒大小对应力－应变曲线的影响

2.4 颗粒屈服强度的影响

以上模拟工作中，BMGCS中所含的颗粒均被视为理想弹塑性的钽颗粒，为了研究颗粒屈服强度对BMGCS拉伸变形行为的影响，在本小节的模拟中，颗粒的材料模型统一采用双线性模型，颗粒体积分数为12%，其代表性体积单元参见图1（f），仅改变颗粒屈服强度σy分别为 0.8 GPa、1.8 GPa、2.8 GPa。

图8展示了三种含不同屈服强度颗粒的BMGCS在单轴拉伸作用下，轴向应变εxx达到7%时的剪切带云图，观察可知，随着颗粒屈服强度增大，剪切带的个数明显增多，如图8（a）中明显的剪切带很少，而图8（b）和图8（c）中，则能够清晰地观察到大量的剪切带，这表明颗粒屈服强度增大，材料的局部剪切程度越小，材料的变形更加均匀，换言之，随着颗粒屈服强度增大，BMGCS的拉伸塑性变形能力有所提高。

图8 εxx为7%时颗粒屈服强度对剪切带的影响

图9 是上述三种含不同屈服强度颗粒的BMGCS在单轴拉伸载荷下的应力－应变关系，从中可知，随着颗粒屈服强度的增大，BMGCS的弹性模量和拉伸屈服强度都有所提高。这里要提出的是，σy的值为1.8 GPa和2.8 GPa时，颗粒的屈服强度已经超过BMG基体的屈服强度，从应力－应变曲线来看，这种情况下颗粒屈服强度的提高对BMGCS拉伸性能的影响不太明显，当颗粒屈服强度σy由0.8 GPa增大到1.8 GPa时，材料在单轴拉伸作用下力学响应水平大幅提高。这一点或许可以为BMGCS的制备时，如何合理选用第二相提供一定的参考。

3 结论

本文通过有限元方法对颗粒增强型块体金属玻璃基复合材料在拉伸载荷作用下的应力－应变曲线以及剪切带的演化进行模拟分析，并进一步模拟分析了颗粒体积分数、颗粒大小以及颗粒屈服强度等细观结构对其拉伸变形的影响，可以得到以下结论：

图9 颗粒屈服强度对应力－应变曲线的影响

（1）在拉伸载荷作用下，剪切带首先在颗粒与基体交界处垂直于载荷方向的区域开始萌生，剪切带的扩展方式基本可以分为两种，其一是以大约45°方向朝着基体边界扩展，另一种则是相对位置大致45°的相邻两个颗粒之间的剪切带互相接近并融合，融合之后的剪切带开始向周围区域扩展以使得该剪切带逐渐变粗。

（2）在一定范围内，随着颗粒体积分数的增大，虽然块体金属玻璃基复合材料的拉伸强度有所降低，但材料内部剪切带个数明显增多，材料在拉伸载荷作用下的局部剪切程度降低，这表明材料的塑性变形能力会有一定的提高。

（3）颗粒的大小对块体金属玻璃基复合材料的应力－应变曲线的影响不太明显，但当颗粒体积分数一定时小体积颗粒意味着个数增多，有助于多重剪切带的形成从而达到增大塑性变形能力的效果。

（4）颗粒强度的增大有助于提升块体金属玻璃基复合材料的拉伸强度。随着颗粒屈服强度增大，剪切带数目增多，这表明材料的局部剪切程度减小，材料的变形更加均匀，材料的塑性变形能力增大。

参考文献：

[1]DUWEZ P,KLEMENT W,WILENS R H.Non-crystalline structure in solidified gold-silicon alloys[J].Nature,1976,187:869-870.

[2]CHEN H S.Thermodynamic considerations on the formation and stability of metallic glasses[J].Acta Metallurgica,1974,22(12):1505-1511.

[3]WANG Q,YANG Y,JIANG H,et al.Superiortensile ductility in bulk metallic glass with gradient amorphous structure[J].Scientific Reports,2014,4(4):4757.

[4]赵燕春,寇生中,袁小鹏,等.Cu-Zr-Al-Nb块体金属玻璃的非晶形成能力和力学性能(英文)[J].稀有金属材料与工程,2015,44(4):791-795.

[5]李春燕,尹金锋,王铮,等.ZrCuNiAlEr块体金属玻璃尺度效应的研究[J].功能材料,2017,48(7):7130-7135.

[6]QIAO J W,SUN A C,HUANG E W,et al.Tensile deformation micromechanisms for bulk metallic glass matrix composites:From work-hardening to softening[J].Acta Materialia,2011,59(10):4126-4137.

[7]SON C Y,KIM G S,LEE S B,et al.Dynamiccompressive properties of Zr-based amorphous matrix composites reinforced with tungsten continuous fibers or porous foams[J].Metallurgical&Materials Transactions A,2012,43(6):1911-1920.

[8]QIAO J,JIA H,LIAW P K.Metallic glass matrix composites[J].Materials Science&Engineering Reports,2016,100:1-69.

[9]CHOI-YIM H,JOHNSON W L.Bulk metallic glass matrix composites[J].Applied Physics Letters,1997,71(26):3808-3810.

[10]JIANG Y,SHI X,QIU K.Numerical study of shear banding evolution in bulk metallic glass composites[J].Materials&Design,2015,77:32-40.

[11]LI J C,CHEN X W,HUANG F L.FEM analysis on the deformation and failure of fiber reinforced metallic glass matrix composite[J].Materials Science&Engineering A,2016,652:145-166.

[12]孙龙港,吴青青,姜云鹏.金属玻璃复合材料压缩增韧的微结构机理[J].能源与环保,2017(11):158-165.

[13]RINTOUL M D,TORQUATOS.Reconstruction of the Structure of Dispersions[J].J Colloid Interface Sci,1997,186(2):467-476.

[14]SEGURADO J,LLORCA J.A numerical approximation to the elastic properties of sphere-reinforced com-posites[J].Journal of the Mechanics&Physics of Solids,2002,50(10):2107-2121.

[15]SPAEPEN F.A microscopic mechanism for steady state inhomogeneous flow in metallic glasses[J].Acta Metallurgica,1977,25(4):407-415.

[16]HUANG R,SUO Z,PREVOST J H,et al.Inhomogeneous deformation in metallic glasses[J].Journal of the Mechanics&Physics of Solids,2002,50(5):1011-1027.

[17]XIA Z,ZHANG Y,ELLYIN F.A unified periodical boundary conditions for representative volume elements of composites and applications[J].International Journal of Solids&Structures,2003,40(8):1907-1921.

[18]王新峰,周光明,周储伟,等.基于周期性边界条件的机织复合材料多尺度分析[J].南京航空航天大学学报,2005,37(6):730-735.

[19]ZHU Z,ZHANG H,HU Z,et al.Ta-particulate reinforced Zr-based bulk metallic glass matrix composite with tensile plasticity[J].ScriptaMaterialia,2010,62(5):278-281.