小学数学中转化思想的渗透

闫万彬

（安徽省阜阳市太和县桑营镇淝南小学）

《义务教育数学课程标准（2011年版）》中指出：“学生通过学习，能够获得适应未来社会生活和进一步发展所必需的重要数学知识以及基本的数学思想方法。”对于中小学生来说，学生面对的各种数学问题，可以简单地分为两类：一类是直接应用已有的知识解答问题；另一种是知识未知，需要应用已知知识来解决的问题。如求它一个长方形的面积，只要知道长方形的长和宽，利用公式，都可以计算出来，这是第一类问题；如果不知道平行四边形的面积公式，通过割补平移把平行四边形转化为长方形，推导出它的面积公式，再计算面积，这是第二类问题。学生在学习数学的过程中所遇到的很多问题都可以归为第二类问题，并且要不断地把第二类问题转化为第一类问题。解决问题的过程，从某种意义上来说就是不断转化求解的过程，因此，转化思想应用非常广泛。

从小学到中学，数学知识呈现出一个由易到难、从简到繁的过程；然而在学习数学、理解和掌握数学的过程中，却需要把陌生的知识转化为熟悉的知识、把繁难的知识转化为简单的知识，从而逐步学会解决各种复杂的数学问题。因此，转化既是一般化的数学思想方法，具有普遍意义；同时也是解决各种复杂问题的法宝之一，具有重要的意义和作用。

带着对转化思想的思考，结合我熟悉的案例，我认为可以从以下几个方面进行渗透。

一、计算中挖掘转化思想

1．计算中的转化

在教学时，引导学生观察算式特点，利用已有知识经验，学生要对算式进行通分计算。通分是一种转化，把异分母分数转化为同分母分数进行计算。

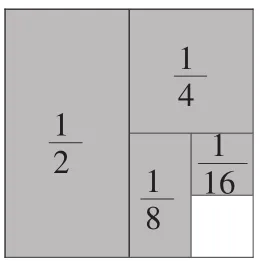
为了促成转化，增加操作环节，师生通过画图的方式将每次对折的部分进行涂色并与算式中的加数一一对应，要想解决涂色部分的面积也就是求算式的和的问题，从而让学生发现要求涂色部分只需用1减去空白部分，达到把原来的加法算式转化成另一个减法算式这也是转化思想与数形结合思想的很好结合；再拓展开来把原式变成让学生展开想象，渗透数学中的极限思想。

2．自主研究中的转化

在教学“分数的大小”时，放手让学生自主研究，可以得出以下一些方法：

方法1：把不同分子的分数化成相同分子的分数。

方法2：把不同分母的分数化成相同分母的分数。

方法3：用画图、折纸等方法实际比一比。

方法4：把分数转化为小数进行大小的比较。

经过比较得出：把分母化成相同的分数比起来快一些。

然后总结得出：把分母不相同的分数转化成和原来分数相等并且分母相同的分数，这个过程叫做通分。

在整个过程中，学生能够应用转化把未知的问题转化为已知的问题进行解决，建立了知识之间的联系。

3．四则运算中“巧用定律”

例如：计算 1.25×32×25 （将 32 分解成 8×4）

=1.25×8×4×25

=（1.25×8）×（25×4）

=l0×l00

=1000

正常计算十分繁琐，利用转化，巧用乘法交换律、结合律计算就显得非常简便。

二、在数学公式推导过程中合理渗透转化思想

转化思想是解决数学问题的一种最基本的数学思想，在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题，我们也常常在不同的数学问题之间互相转化，可以说在解决数学问题时转化思想几乎是无处不在的。

如平行四边形、三角形、梯形、圆形等图形的面积公式推导，它们均是在学生认识了这些图形，掌握了长方形面积的计算方法之后安排的，是整个小学阶段平面图形面积计算的一个重点，也是整个小学阶段中能较明显体现转化思想的内容之一。教学这些内容，一般是将要学习的图形转化成已经学会的图形，在引导学生比较之后得出将要学习图形的面积计算方法。随着教学的步步深入，转化思想也渐渐进入学生的头脑中。

三、综合应用中巧用转化思想解决问题

如在教学长方体复习课时，在表面积解决问题中巧妙利用转化思想解决卫生箱涂漆问题。教学环节如下：

师：卫生箱的哪些面需要涂油漆？

生1：外边的前后左右和外边的底面以及里面的前后左右和内底面。

生2：还有四周的沿儿也要涂上油漆。

师：要求这些涂漆面积，可以怎样求呢？

生3：我们小组通过研究可以这样求涂漆面积：把内底上的面平移上来，与沿儿平行成一个大的面，这样就可以先求出大长方体的表面积和里面四壁的面积就行了。

教学中结合学生汇报，用课件演示平移方法，培养了学生空间观念，突破难点。并且渗透了转化思想。

在小学数学教学中，提倡学生拥有多元化的数学思想，转化思想是解决数学问题的一种最基本的数学思想，所以在教学中要渗透转化思想，要引导学生用数学的眼光去观察事物，从数学的角度去思考问题，逐步提升学生的数学素养。