三类图的拉普拉斯谱半径的极限点

李静花， 何常香

（上海理工大学 理学院，上海 200093）

1 问题的提出

设为阶 简单连通图，其中，是图的 点集合，是图的边集合。定义的 度对角矩阵，其 中 ，(表 示)点的度；若拉普拉斯矩阵为半正定奇异矩阵，设其特征值为。将图的 最大拉普拉斯特征值称为图的 拉普拉斯谱半径，记为。对于图的拉普拉斯矩阵的特征多项式简记为。

1972年，Hoffman[1]研究了图的特征根的极限点，并给出了图的特征根的极限点的定义。类似地，本文给出图的拉普拉斯谱半径的极限点的定义。

定义1 对于实数，若存在一个图序列，使得则称实数是图的拉普拉斯谱半径的极限点。

文献[2]研究了以下3类图的拉普拉斯谱半径的极限点：连通图中 某1点与的1端通过1条边相连（如图1所示）；连通图中某1点与2条内点不交的的1端分别通过1条边相连（如图2所示）；的2个端点分别与2个顶点不相交的二部连通图，中某1点通过1条边相连（如图3所示）。文献[3]研究了图的拉普拉斯特征值极限点集合的性质，并确定了树的代数连通度极限点前2大的值；文献[4]研究了代数连通度极限点的性质，并确定了树的代数连通度前4大的值；文献[5]确定了树的代数连通度极限点的第5～14大的值。

图1 Fig.1

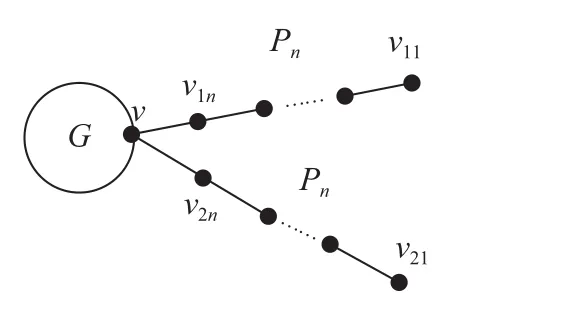
图 2G:(Pn,Pn)Fig.2G:(Pn,Pn)

图3 (G,H):PnFig.3(G,H):Pn

本文主要研究如下3类图的拉普拉斯谱半径的极限点：连通图中1点与多条内点不相交的的1端点粘连（如图4所示）；连通二部图中 1点与1个中1点粘连（如图5所示）；至少含1条边的连通二部图中1点与多个顶点不相交的中1点粘连（如图6所示）。

图 4Gv(s,n)Fig.4Gv(s,n)

图 5G·CnFig.5G·Cn

图6 (s,n)Fig.6(s,n)

本文直接引用的其他术语和记号参见文献[6]。

2 主要引理

现介绍一些本文证明中需要用到的引理。

设是 简单连通图，是图添 加1条新边后所得的图，即。

引理1[7]图和图的拉普拉斯特征值满足交错定理，即

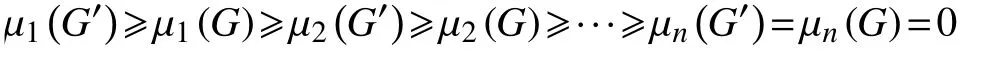
推论1 若是图的子图，则有

进一步地，若是图的 真子图，和的拉普拉斯谱半径有引理2的关系。

引理2[8]若是连通二部图的真子图，则有

引理3[9]对于图，有

若是连通图，则等式成立当且仅当是二部正则图或二部准正则图。

3 主要结果

图 7Pv(3,2)Fig.7Pv(3,2)

参考文献：

[1]HOFFMAN A J. On limit points of spectral radii of nonnegative symmetric integral matrices[M]//ALAVI Y, LICK D R, WHITE A T. Graph Theory and Applications. Berlin,Heidelberg： Springer, 1972, 303： 165-172.

[2]GUO J M. On limit points of Laplacian spectral radii of graphs[J]. Linear Algebra and its Applications, 2008,429(7)： 1705-1718.

[3]GUO J M. The limit points of Laplacian spectra of graphs[J]. Linear Algebra and its Applications, 2003, 362：121-128.

[4]KIRKAND S. A note on limit points for algebraic connectivity[J]. Linear Algebra and its Applications, 2003,373： 5-11.

[5]LIU Ying. The ordering of limit point of algebraic connectivity of trees[J]. Journal of Natural Science of Heilongjiang University, 2008, 25(1)： 103-106.

[6]BONDY J A, MURTY U S R. Graph theory with applications[M]. London： The Macmillan Press Ltd, 1976：6-258.

[7]GRONE R, MERRIS R, RSUNDE V S. The Laplacian spectrum of a graph[J]. SIAM Journal on Matrix Analysis and Applications, 1990, 11(2)： 218-238.

[8]GUO J M. On the Laplacian spectral radius of a tree[J].Linear Algebra and its Applications, 2003, 368： 379-385.

[9]ANDERSON W N JR, MORLEY T D. Eigenvalues of the Laplacian of a graph[J]. Linear and Multilinear Algebra,1985, 18(2)： 141-145.

[10]MERRIS R. Laplacian matrices of graphs： a survey[J].Linear Algebra and its Applications, 1994, 197/198：143-176.

[11]GUO J M. The Laplacian spectral radius of a graph under perturbation[J]. Computers & Mathematics with Applications, 2007, 54(5)： 709-720.

[12]GUO J M. A conjecture on the algebraic connectivity of connected graphs with fixed girth[J]. Discrete Mathematics, 2008, 308(23)： 5702-5711.

[13]GUO J M, LI J X, SHIU W C. On the Laplacian, singless Laplacian and normalized Laplacian characteristic polynomials of a graph[J]. Czechoslovak Mathematical Journal, 2013, 63(3)： 701-720.