混凝土冲击拉伸力学性能及裂纹扩展试验研究和数值模拟

戚亚珍 张 华 郭继鑫

(河海大学 土木与交通学院， 南京 210098)

混凝土的破坏过程实际上是微裂缝的产生、扩展、贯通，直到导致混凝土结构失稳破坏．动态荷载下裂纹的扩展以及结构的破坏更加严重，因此研究混凝土动态荷载下的抗拉性能和裂纹扩展具有重要的指导意义和参考价值．

目前多采用断裂韧性来研究混凝土裂缝的开裂、扩展和贯通，分析混凝土在高应变率下的变形和破坏机理[1]．学者们先后采用诸如三点弯曲梁、V形切槽巴西圆盘、中心直裂纹巴西圆盘等来测试材料的断裂韧性，其中尤以巴西试验方法应用最为广泛[2-3]．巴西试验最早用于岩石断裂性能的研究，并取得了一定的成果．但是由于冲击荷载的复杂性和混凝土材料更为明显的各向异性，使得混凝土材料巴西试验的有效性需要进一步的研究．同时在动态荷载下，试件在极短时间内破坏，数值模拟能有效弥补试验很难观察其裂纹的萌生和扩展的缺点．近年来扩展有限元理论得到了较大的发展，Chessa J[4]等采用时间、空间扩展有限元法来解决双曲线问题的不连续性，Eftekhari M[5]等使用XFEM多尺度模型对碳纳米管混凝土的力学性能和断裂性能进行了研究，扩展有限元理论已成为迄今为止求解不连续问题的最有效方法．

本文利用Ф74 mm分离式霍普金森压杆试验装置对混凝土平台巴西圆盘试件进行了劈裂拉伸试验，研究不同加载角对混凝土平台巴西圆盘试件起裂方式及破坏模式的影响，得到用于测试混凝土动态力学性能的最优加载角．基于最优加载角测得试件的劈裂拉伸应力-径向应变曲线，分析了混凝土抗拉强度、峰值应变、拉伸敏感系数的应变率效应．并利用ABAQUS中的扩展有限元法对试件破坏过程进行模拟，将模拟得到的裂纹扩展结果与试验结果进行了对比．

1 试验设计

1.1 试验原理

SHPB试验中需要遵循一维应力波假设和应力均匀假设．根据一维应力波假定及应力均匀性假设(εt=εi+εr)，并根据测得的3个脉冲信号，即可求得试件的应力应变．

(1)

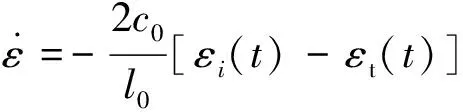
(2)

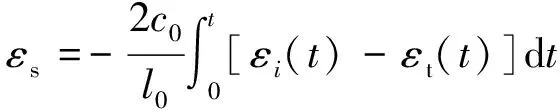
(3)

其中，E、A、C0分别为杆的弹性模量、截面积及弹性波速；As、l0分别为试样的初始截面面积和厚度．

试件的起裂时间采用应变片法确定[6-7]：设定试件上应变信号发生突变的时刻为试件起裂时刻，应变最先发生突变的点为试件起裂点．图1为试件加载角及应变片粘贴示意图．

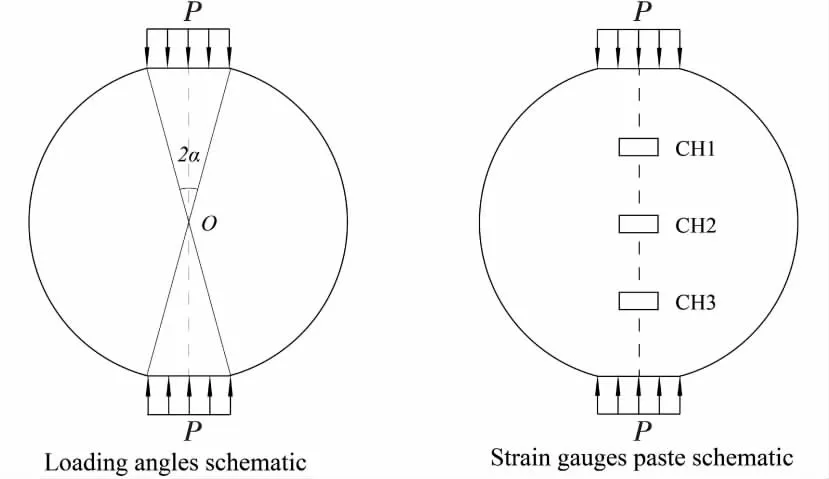
图1 试件加载中心角及应变片粘贴示意图

1.2 试件制备

共制备3种强度的混凝土试件，强度等级分别为C25、C35、C45；不同加载角巴西圆盘加载角度2α分别为10°、20°、30°．3种不同强度等级混凝土具体配合比见表1．

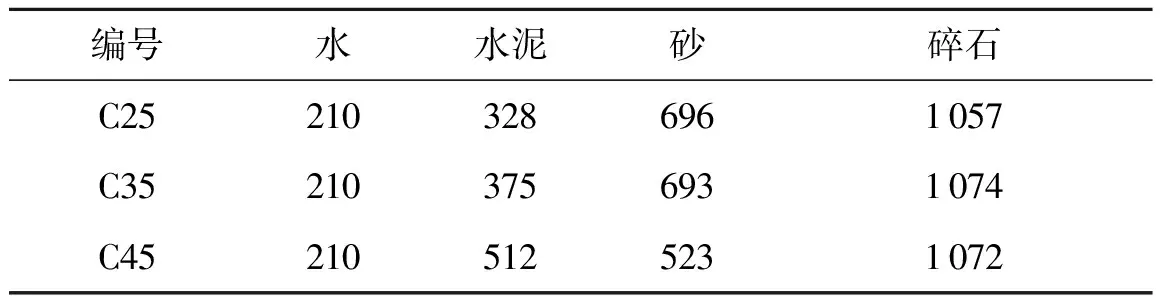
表1 混凝土配合比 (单位：kg/m3)

水泥采用南京海螺牌32.5级硅酸盐水泥，粗骨料选用最大粒径为9.5 mm的瓜子片，砂选用黄砂，晒后粒径控制在0～3 mm之间，水为自来水．将混凝土浇筑在钢模内，待强度发展完全后取芯、切割成圆柱体试件，试件尺寸为Ф74 mm×30 mm．

试验将在静态力学性能的基础上研究混凝土动态力学性能及裂纹扩展，静态试验结果仅作为对比，故不单独列出．为保证试验结果的可靠性，对传统的SHPB试验方法进行了改进，引进万向头技术和波形整形技术，并在杆件端部涂抹凡士林以减少摩擦[8-10]．

2 试验与数值模拟结果分析

2.1 平台巴西圆盘的裂纹扩展结果

2.1.1 平台巴西圆盘裂纹扩展试验结果

利用分离式霍普金森压杆对加载中心角分别为10°，20°，30°的平台巴西圆盘进行加载，由于在试验过程中较难观察试件的开裂及裂纹扩展过程，故在试件上粘贴应变片以记录试验中各点应变的变化历程，得到不同加载角试件各点的应变历程曲线，如图2所示．同时得到试件在静动态加载条件下的破坏形态，如图3所示．

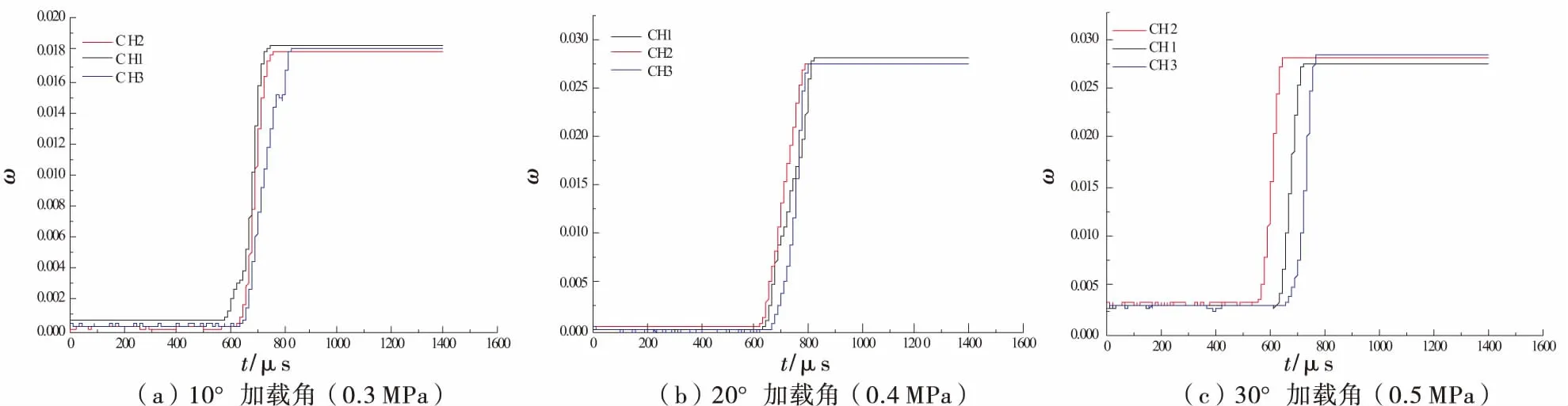
图2 不同加载中心角应变片应变历程

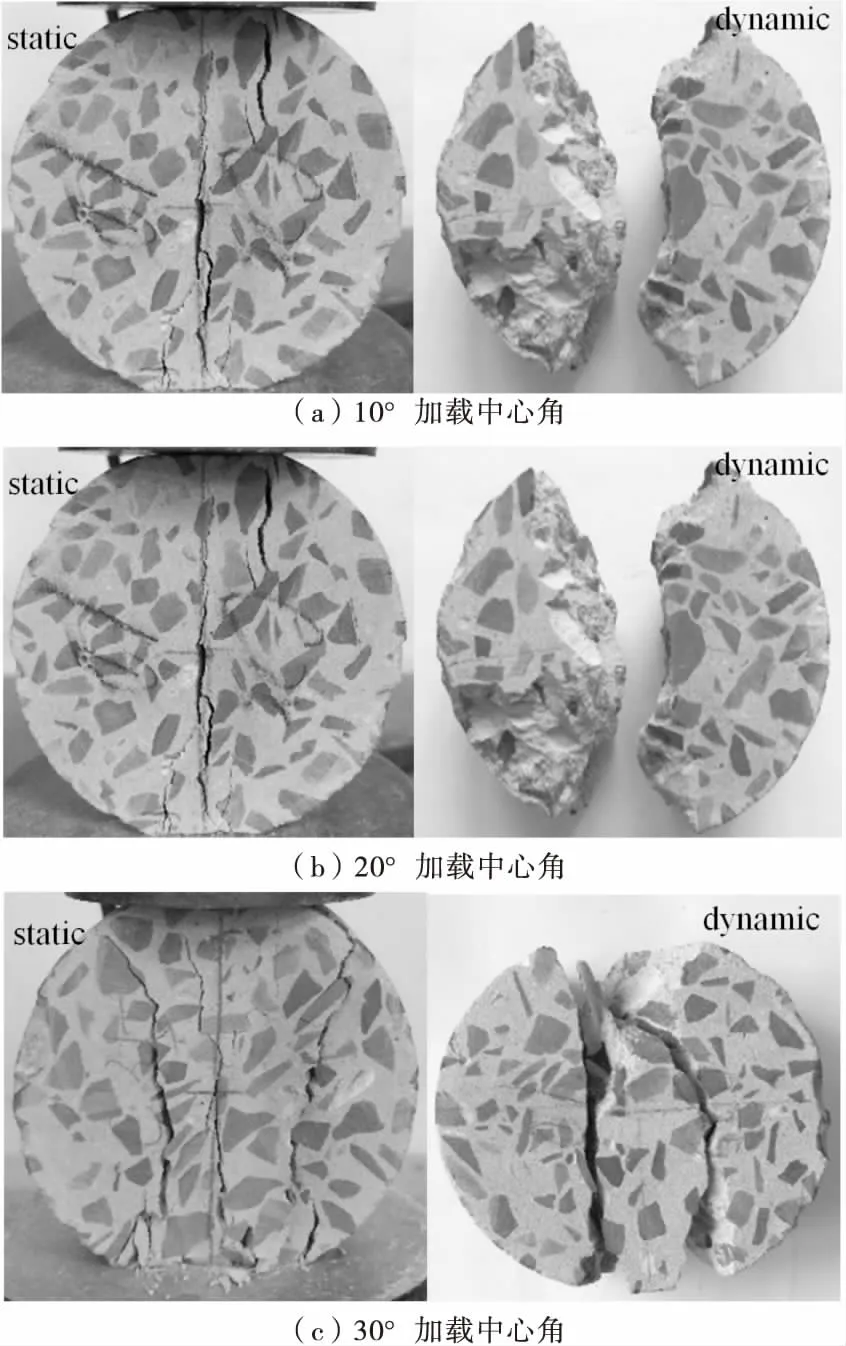
图3 静态和动态试件破坏形态对比

图2显示，10°加载角时应变片CH1最先开裂，然后沿加载直径向中心扩展，即试件开裂始于近入射端处，而不是试件中心；加载角为20°和30°时，试件均为CH2应变片最先开裂，即裂纹始于试件中心．这表明较小角度加载角不能明显改善应力集中现象，而当加载角增大到20°时，应力集中现象得到改善．

由图3可以看出，在动态加载条件下，裂纹沿试件受力方向扩展，试件最终沿加载直径方向劈裂为两半，且在加载端部产生三角形破坏区域，并在中部产生剪切带．三角形区域的产生是由于端部应力集中，并随着应变率增大而趋于不明显．中部剪切带是由试件与杆件之间的摩擦效应引起的，随着加载角增大，剪切带也加宽．同时对比静态破坏形态可以发现，在静态荷载下，试件沿砂浆和骨料的界面破坏．而在动态冲击下，裂纹穿过骨料而发生破坏．这是因为，在动态冲击下，试件吸收较大的能量，裂纹来不及沿着界面扩展而使试件发生骨料破坏．

2.1.2 平台巴西圆盘裂纹扩展数值模拟结果

利用基于ABAQUS的扩展有限元法对10°和20°平台巴西圆盘裂纹扩展过程进行数值模拟．建模时假定材料为理想的线弹性材料，预设直裂纹长度为2 mm，分别对应SHPB冲击试验中粘贴应变片的位置．采用基于损伤力学演化的失效准则，损伤起始判据为最大主应力失效准则．混凝土强度等级为C35，轴心抗拉强度取ft=1.57 MPa，弹性模量、泊松比分别为E=33.2 GPa，υ=0.3．

图4和图5分别为10°和20°平台巴西圆盘试件数值模拟结果．

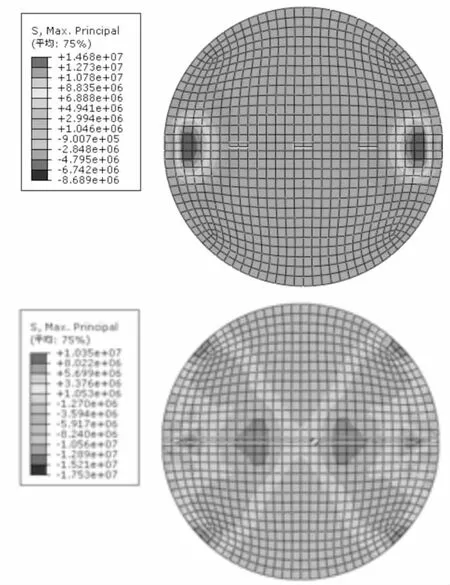
图4 10°巴西圆盘最大应力云图(单位：MPa)

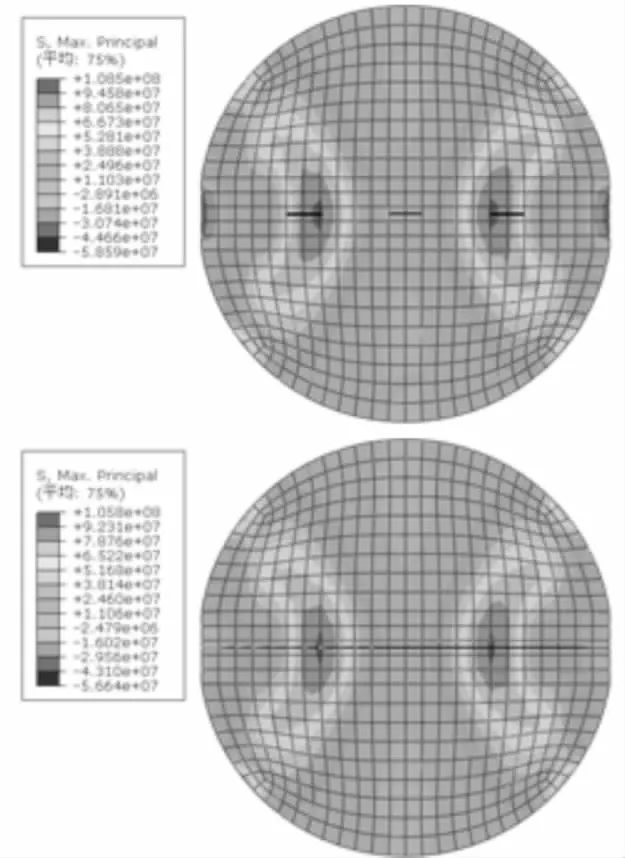
图5 20°巴西圆盘最大应力云图(单位：MPa)

从图4可以看出，10°巴西圆盘两平台端有很大应力集中，最大主应力随着载荷从两平台端向圆盘中心传播，当左右两条对称裂纹裂尖最大主应力达到最大主应力的损伤判据临界值，裂尖处的单元始失效导致裂尖开裂．图5显示，20°平台巴西圆盘两端应力集中现象并不明显．随着应力从两平台端向圆盘中心扩散，当裂尖应力达到最大主应力时，裂尖处单元开始失效导致中心裂尖开裂，即裂纹开始于圆盘中心随后向两平台端扩展直至断裂．

2.1.3 试验结果与数值模拟对比

对比有限元模拟结果与试验结果，ABAQUS扩展有限元法模拟裂纹起裂、扩展直至完全破坏的过程与2.1.1节所得试验结果一致，即10°加载平台巴西圆盘存在较大应力集中而20°加载角可以保证圆盘中心起裂，裂纹沿加载直径方向扩展．这一结论验证了试验结果的正确性， 同时证明了使用扩展有限元模拟裂纹扩展是有效的．

2.2 20°平台巴西圆盘SHPB试验结果

根据上文分析，20°加载角可以保证圆盘中心起裂，且试件从中心劈裂为两半，满足巴西试验原理，用于测定混凝土拉伸强度是可靠的．故使用20°平台巴西圆盘进行劈裂拉伸试验，测试混凝土力学性能．

对试验数据进行处理，得到试件应力应变曲线,由于篇幅所限，本文仅列出C35、C45试件的应力应变曲线如图6、图7所示．结合二波法计算公式，求得不同应变率下试件的抗拉强度，将结果示于表2．

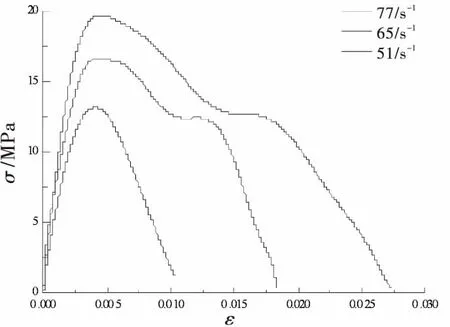
图6 C35 20°平台巴西圆盘应力-应变曲线

图7 C45 20°平台巴西圆盘应力-应变曲线

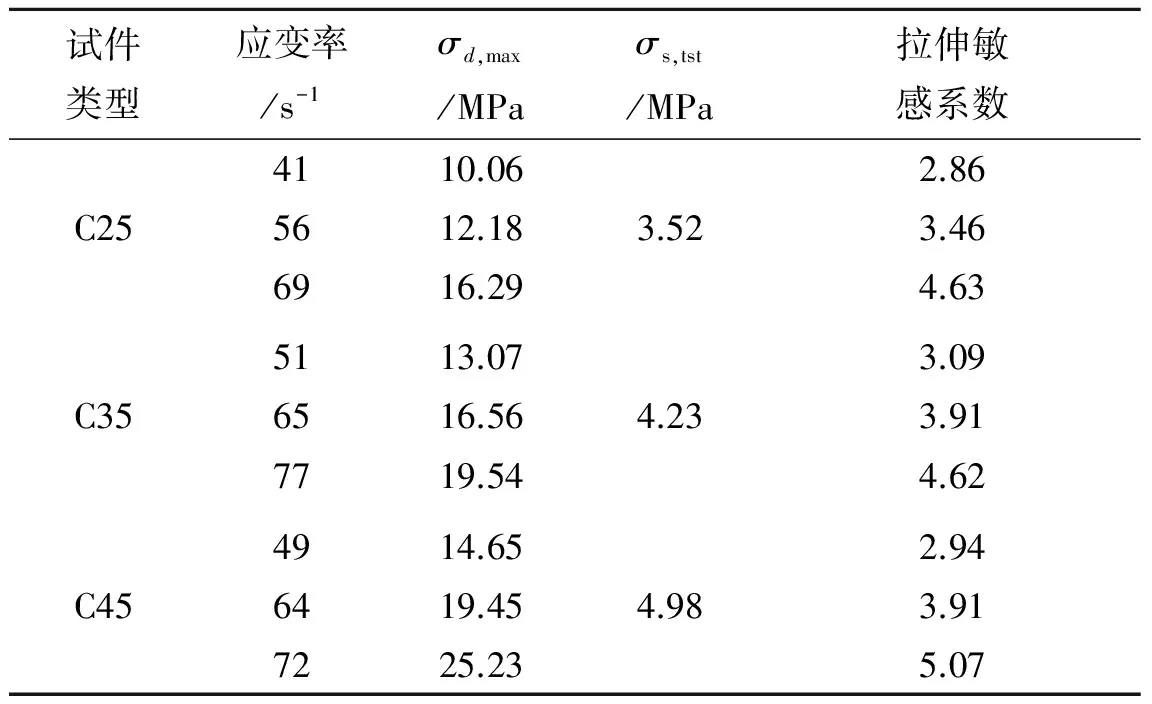
试件类型应变率/s-1σd，max/MPaσs，tst/MPa拉伸敏感系数4110．062．86C255612．183．523．466916．294．635113．073．09C356516．564．233．917719．544．624914．652．94C456419．454．983．917225．235．07

图8为极限应力与应变率关系曲线，图9为极限应变与应变率的关系曲线．其中拉伸敏感系数(Tensile Sensitive Coefficient)为动态拉伸强度与静态拉伸强度的比值 ，反映混凝土劈裂拉伸强度的应变率效应．

图8 极限应力-应变率曲线

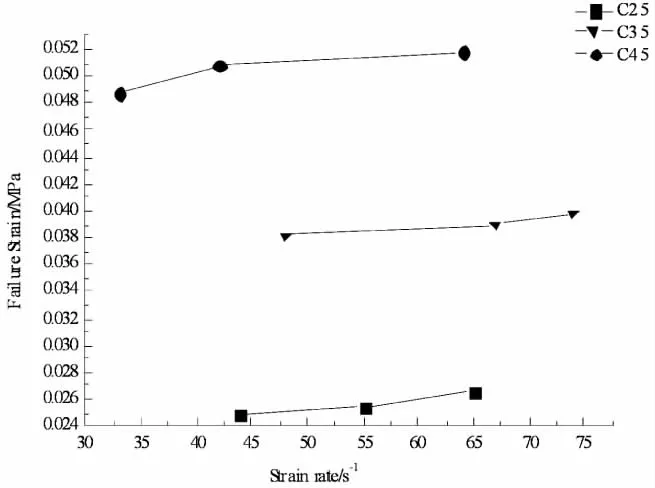
图9 极限应变-应变率曲线

表2显示，动态拉伸强度约为静态拉伸强度的3～5倍，表现出明显的应变率效应；同时可以看出，混凝土的拉伸敏感系数也随着应变率提高而增大，即随着应变率提高，应变率效应也随之增强．图6～9显示，对于同一配合比的混凝土，试件破坏极限应力和极限应变均随应变率提高而增大，且应变率越高，增大幅度越大．对比图8和图9可以发现，混凝土极限应力的应变率效应比极限应变更加明显，随着应变率增加，极限应力增大幅度也更大．

3 结 论

基于试验和数值模拟结果，主要得出如下结论：

1)不同加载中心角平台巴西圆盘对比，10°加载角不能明显改善应力集中以使试件在中心开裂．20°加载中心角可以保证试件在冲击荷载下中心部位起裂，而且不会出现类似30°加载角试件产生次生裂纹的现象．利用平台巴西圆盘测量混凝土动态力学性能时，20°加载中心角更为合理．

2)在冲击荷载下，试件表现为骨料破坏．试件沿加载端产生三角形破坏区域，应变率较高时，试件产生剪切破坏带．

3)混凝土动态力学参数具有明显的应变率效应，且极限应力的应变率效应比极限应变更加明显，随应变率提高增大幅度也更大．

4)数值模拟结果表明10°平台巴西圆盘应力集中现象严重，且裂纹始于平台两端，而20°平台巴西圆盘裂纹起始于中心并向两端扩展，这与试验结果一致，因此用扩展有限元方法模拟裂纹扩展是有效的．

参考文献：

[1] 王剑英．混凝土试件及其衬砌结构破坏过程的数值模拟研究[D]．哈尔滨：哈尔滨工程大学，2007．

[2] 金 剑,雷 冬,朱飞鹏,等．混凝土损伤应变与微裂纹的实验研究[J]．科学技术与工程,2014,14(14):266-268．

[3] 张 华,郭继鑫,傅玉珍,等．冲击作用下混凝土裂纹扩展试验研究及数值模拟[J]．振动与冲击,2016,35(17):107-112．

[4] Chessa J, Belytschko T． A local space-time discontinuous finite element method [J]． Computer Methods in Applied Mechanics and Engineering, 2006, 195:1325-1343．

[5] Eftekhari M, Ardakani S H, Mohammadi S． An XFEM multiscale approach for fracture analysis of carbon nanotube reinforced concrete [J]． Theoretical & Applied Fracture Mechanics, 2014, 72(1):64-75．

[6] Weisbrod G, Rittel D． A method for dynamic fracture toughness determination using short beams [J]． International Journal of Fracture, 2000, 104(1): 89-103．

[7] 樊 鸿，张 盛．用应变片法确定混凝土动态起裂时间的研究[J]．振动与冲击，2010,29(1):153-157．

[8] 巫绪涛,胡时胜,杨伯源,等．SHPB技术研究混凝土动态力学性能存在的问题和改进[J]．合肥工业大学学报,2004,27(1):63-66．

[9] 刘剑飞,胡时胜,王道荣．用于脆性材料的Hopkinson压杆动态实验新方法[J]．实验力学,2001,16(3):283-290．

[10] 孟益平,胡时胜．混凝土材料冲击压缩试验中的一些问题[J]．实验力学,2003,18(1):108-112．