基于WIM数据的公路桥梁交通荷载水平研究

2018-05-21汪永兰陈伟健

交通科技与经济 2018年3期

汪永兰，陈伟健

(中设设计集团股份有限公司，江苏南京 210014)

近年来，随着交通基础设施的逐步完善以及经济建设的不断发展，公路交通运输负荷也越来越繁重，主要体现在以下两方面：一是交通运输需求不断攀升[1]；二是实际交通车辆的总重和轴重增大，超载问题日益突出[2]。准确认识桥梁实际交通荷载水平，对分析桥梁结构损伤原因、评估桥梁结构安全具有重要意义。

《公路桥涵设计通用规范》(JTGD60-2004)[3]，以下简称为《04桥梁通规》。汽车荷载模型的确定立足于20世纪90年代对国道干线4个测点的实际交通车辆数据。在确定汽车荷载模型的过程中，虽然通过随机过程考虑有100年设计基准期内汽车荷载理论平稳发展情况，但随着经济社会近20年的发展，当前的实际运营交通汽车荷载状况已经有了较大变化。表1所示为交通部综合规划司公布的2006—2012年公路货运运输量相关统计信息[4]。我国干线公路存在部分桥梁运营时间较短但实际服役状态恶化较快现象，虽然桥梁损坏的原因复杂，但交通荷载的影响是其中的重要因素。

对实际交通荷载水平的发展变化业界已进行了较多研究。

2010年李嘉维[5]根据某高速公路实际行车状况，根据实际车辆类型、车重和轴距分布，利用统计方法得到8类标准车辆荷载模型。2010年杨琪[6]利用WIM系统调查佛开高速的实际车辆荷载，借助Rice公式计算10～35 m中小跨径简支梁、三跨25～45 m连续梁关键截面在实际汽车荷载作用下的效应值，研究实际车辆荷载效应与规范车辆荷载效应的差别。2011年梁栋[7]以WIM调查数据为基础进行统计分析，利用蒙特卡洛方法生成模拟车流，并分析研究了广泛使用的简支梁桥和连续梁桥的荷载效应(见表1)。

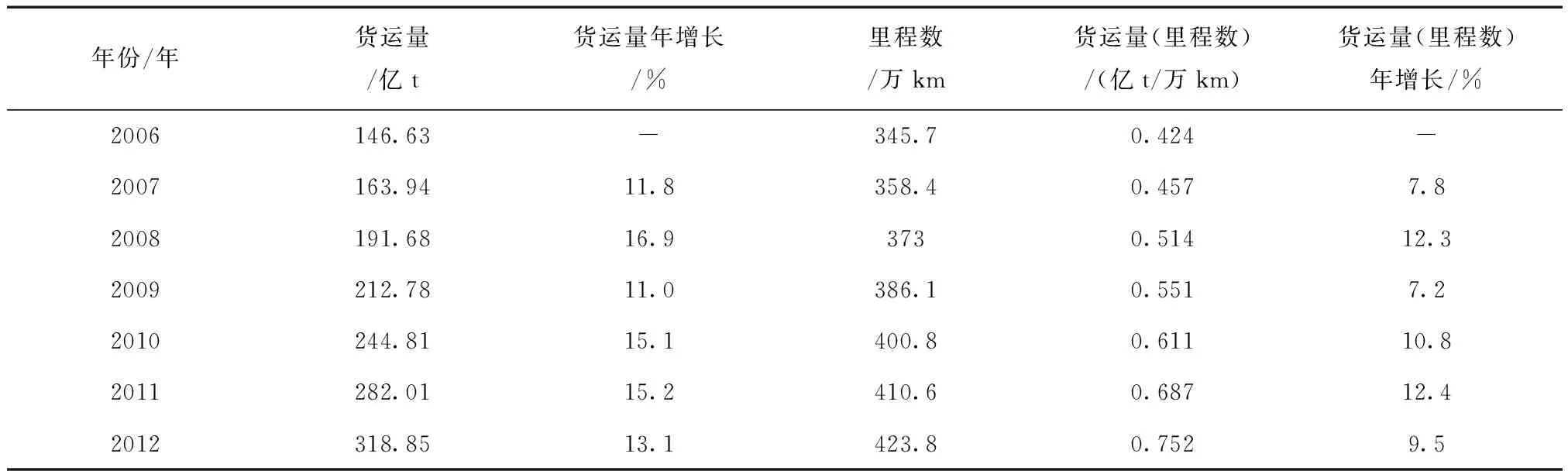
表1 公路货运量及公路总里程

2013年宗周红[8]基于动态称重系统实测数据得出京沪高速沂淮段新沂河大桥实际运行车辆荷载水平。2014年张征文[9]基于WIM系统采集实测数据，以单车过桥情形分析了实际交通车辆荷载作用下跨径为6～50 m的12种简支梁桥结构内力分布规律，并与现行桥梁设计规范中汽车荷载对应的效应值进行对比。

相关文献对实际交通车辆统计参数进行了较为详尽的分析，计算了某一座或某一类桥梁结构在实际车辆作用下的荷载效应值，并与《04桥梁通规》汽车荷载对应值进行比较。2015年阮欣[10]总结了当前桥梁荷载效应极值外推的主要方法，并指出采用不同的外推方法可能导致不一致的结果。当前桥梁交通荷载水平分析存在的主要问题在于：相关研究仅将《04桥梁通规》汽车荷载模型当作对比荷载工况进行计算，忽视其本身含有的可靠度概念，或者并没有按照规范交通荷载模型实际获取过程进行同过程比对。本文拟针对这一问题，暂以单个桥梁为例，利用实测WIM数据研究桥梁的实际交通荷载水平。

1 实际交通荷载水平分析方法

1.1 《04桥梁通规》汽车荷载模型计算

《04桥梁通规》汽车荷载模型的计算，文献[3，11，12]给出了较为详细的过程：

1)选择具有代表性的国道干线207(山西晋城)、328(江苏扬州)、305(辽宁盘锦)、101(河北承德)等4个测点，详细记录连续5天共计6万多辆机动车观测记录的交通车辆荷载数据，信息量包括车重、轴重、轴距、车速、车辆通过测点的时刻等。

2)以剔除了异常值的实测自然车队作为加载主体，选择具有代表性的简支梁、连续梁结构进行系统加载，得到对应荷载效应值S。

3)对得到的荷载效应值S最大值样本进行概率分布假设检验，得到对应概率分布模型，并以此为截口分步计算100年设计基准期内某一分位值Sm。

4)以《公路桥涵设计通用规范》(JTJ 021-89)规定的汽车荷载模型汽-20及汽-超20为加载主体，同样加载在第2)步所述的桥梁结构上，得到对应荷载效应值Q，并将对应效应比值KSQ=Sm/Q作为统计分析目标量。

5)按照测点位置、计算结构类型等因素对KSQ进行归并处理，并进行概率分布假设检验。按照不同概率、不同分位值确定荷载效应标准值、频遇值和准永久值，其中荷载效应标准值对应0.95分位值。

1.2 单个桥梁荷载水平计算

针对单个桥梁实际交通荷载水平的计算分析过程更为简单，即取1.1节中的前3步进行对应分析即可。

1)确定加载车队。如果在目标桥梁所在的封闭公路上布置WIM系统，可直接获得目标桥梁的实际交通荷载数据。如果目标桥梁所在封闭线路没有WIM系统，则需要综合目标桥梁附近测点的实测数据和路网交通流分析，得到符合实际的加载车队。或根据本区域交通车辆统计分析概率模型，按照Monte Carlo的方法生成模拟车流。

2)获取荷载效应时程曲线。选择目标桥梁所有关键截面对应荷载效应，计算其影响线后的加载车队，得到对应的目标时程曲线。

3)计算荷载效应样本。根据已获取的荷载效应时程曲线选取时间步长划分等长时间单元，然后提取每一个时间单元内的目标荷载效应最大值，并进行概率分布假设检验。

4)随机过程截口分布统计分析。将实际统计时间段的目标荷载效应最大值概率分布作为截口分布，根据平稳二项随机过程的类别，外推100年内目标荷载效应的概率目标分位值。

2 实例计算

2.1 工程概况

选择某预应力变截面悬臂现浇连续箱梁作为工程案例进行计算。桥梁上部结构跨径组合为(62+100+62) m，上部结构采用单箱单室箱梁，纵、横、竖三向预应力体系，桥宽12.75 m，箱梁根部梁高5.8 m，跨中梁高2.5 m，箱梁顶板宽12.75 m，底板宽6 m，翼缘板悬臂长3.375 m。该桥位于104国道交通繁忙路段，荷载等级为公路Ⅰ级，2010年12月建成通车。2013年3月作为相邻国道桥梁改建时期交通引流通道，交通服役任务加重。2013年在日常养护中发现受力裂缝，2014年3月被评定为4类桥梁。初步分析桥梁结构损伤与超载车辆通行关系密切[13-14]，2014年5月开始对桥梁按照四类桥进行管理养护，即按照《公路桥涵养护规范》(JTG H11-2004)中条文规定进行交通管理。2014年12月开始对该桥进行加固方案设计，2015年5月完成现场加固施工，同期为进一步加强交通车辆管制，在上桥头设置限高装置(限高2.8 m)，如图1所示，并安装专门的车辆动态称重系统(Weight-In-Motion, WIM)。WIM系统能提供车型、车轴重、车辆过称重断面时间、车速、车辆所在车道等信息。为节省篇幅，本次分析仅选择该桥中跨跨中截面弯矩作为目标截面效应值进行计算(见图1)。

图1 通行车辆限高装置

2.2 计算假定

1)车辆通过WIM称重断面后进行匀速运动；

2)车辆在行驶过程中不更改车道；

3)允许后一辆车赶超前一辆车的情形。

2.3 计算过程及结果

本次计算使用桥梁新安装的WIM系统获取的2015年10月—2016年4月共233 d的称重数据。运用MIDAS/civil软件建立该桥有限元仿真模型，并计算中跨跨中截面弯矩的影响线。以单位时间步长模拟实际交通车辆连续驶过桥面的过程，并记录每一时刻中跨跨中截面弯矩值，得到对应的时程曲线。以1 d作为时间区段，编程计算每个时间区段内中跨跨中截面弯矩的最大值样本。

对得到的中跨跨中截面弯矩最大值样本分别进行Gamma分布、正态分布、对数正态分布、Laplace分布、Pareto分布、Beta分布、指数分布、威布尔分布、极值I型分布，并进行参数估计及假设检验[15]。由计算结果可知，在检验水平为0.05时通过χ2检验及K-S检验不排除中跨跨中截面的正弯矩，最大值符合Laplace分布，此外正态分布逼近满足检验条件，如图2所示。

综合考虑Laplace分布及正态分布所代表的概率含义，本文认为中跨跨中截面正弯矩最大值符合正态分布

本次分析是以2015年10月—2016年4月共计233 d的实测车载数据为依据，对应时间单元内控制截面弯矩最值服从正态分布，对应概率分布函数为F(x)，并认为233 d的数据样本能代表一年实际荷载通行情况。据此以1年数据推导100年设计基准期内最大值概率分布函数Fm(x)的表达式为

Fm(x)=[F(x)]n.

式中：n为对应于平稳二项随机过程的时间截口比值，在本次计算中n为100。

以汽车荷载标准值作为对比项，取100年设计基准期内目标荷载效应最值分布为0.95分位值，与《04桥梁通规》汽车荷载效应标准值相对应，即

Fm(x)=0.95.

则

F(x)=(0.95)1/100=0.999 49.

计算得到中跨跨中截面正弯矩的最值概率分布目标分位值为15 048 kN·m。按照《04桥梁通规》加载汽车荷载得到中跨跨中截面正弯矩标准值为19 133 kN·m，对应荷载的效应系数为

即在当前的交通管制条件下，对记录的实际通行交通荷载数据按规范交通荷载模型获取过程进行同过程计算分析，得到目标桥梁中跨跨中截面正弯矩效应，与设计采用的标准值比较后表明未超载。该桥在加固后经交通管制，桥梁状况比较平稳，没有产生新的病害。