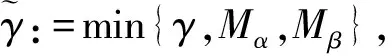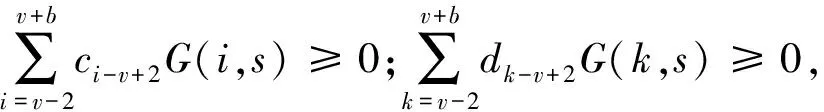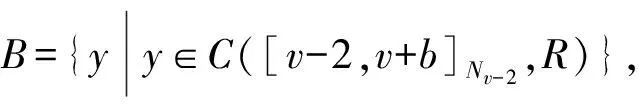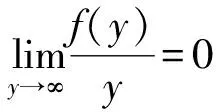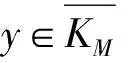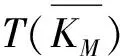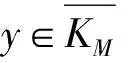带非局部条件的分数阶差分方程边值问题三个正解的存在性
2018-05-21张慧芬康淑瑰李艳郭建敏
张慧芬,康淑瑰,李艳,郭建敏
(1.山西大同大学 数学与计算机科学学院, 山西 大同 037009;2.山西师范大学 数学与计算机科学学院, 山西 临汾 041000)
0 引言
近年来连续型的分数阶微积分已被广泛的研究, 相对而言,离散型的分数阶微积分发展比较缓慢, 对其解或正解的存在性和多解性的研究便是其中之一, 见文献[1-6]。其次,离散型的分数阶微分方程边值问题变号解和无解的情况也受到许多作者的关注, 见文献[7-9]。在本文中, 我们将讨论下面的带非局部条件的分数阶离散边值问题
-Δvy(t)=λh(t+v-1)f(y(t+v-1))
(1)
y(v-2)=Ψ(y),
(2)
y(v+b)=Φ(y),
(3)
其中1 关于分数阶差分的一些基本知识在这里不再详细引入,具体参看文献[1]。 引理1[1]对任意的t和v有Δt(v)=vt(v-1). 引理2[1]令0≤N-1 Δ-vΔvy(t)=y(t)+c1t(v-1)+c2t(v-2)+…+cNt(v-N), 这里ci∈R,1≤i≤N. 引理3[2]令1 -Δvy(t)=h(t+v-1),y(v-2)=0=y(v+b) 的唯一解为 其中G:[v-2,v+b]Nv-2×[0,b]N0→R为 (4) 引理4[2]由(4)定义的Green函数满足下列性质: (1)G(t,s)≥0其中(t,s)∈[v-2,v+b]Nv-2×[0,b]N0; (3)存在一个数γ∈(0,1)满足 其中s∈[0,b]N0. 定理1 令f:[0,∞)→[0,∞),Ψ,Φ∈C([v-2,v+b]Nv-2,R)是给定的函数,函y(t)是分数阶离散边值问题(1)-(3)的解当且仅当它是算子 (5) 的不动点,其中 (6) (7) 而G(t,s)是引理3中给定的Green函数。 证明由引理2, 我们可得(1)-(3)的解为 y(t)=-Δ-vλh(t+v-1)f(y(t+v-1))+c1t(v-1)+c2t(v-2). 由边值条件(2)可得 c2Γ(v-1)=c2Γ(v-1)=Φ(y) 所以 故得 故证得y(t)是问题(1)-(3)的解当且仅当y(t)是(5)的不动点。 引理5[10]函数α(t)在[v-2,v+b]Nv-2上关于t严格递减,并且 函数β(t)在[v-2,v+b]Nv-2上关于t严格递增,并且 定义1[11]设P是实Banach空间E中的一个锥。 若映射θ:P→[0,∞)连续, 且对任意的x,y∈P以及0≤t≤1,有θ(tx+(1-t)y)≥tθ(x)+(1-t)θ(y)成立, 则称映射θ是实Banach空间E中锥P上非负连续凹泛函。 假设r,a,b是正数,我们引入以下记号 (H1) {u∈P(θ,a,b):θ(u)>a}≠Ø且对于所有的u∈P(θ,a,b)有θ(Au)>a; (H3)θ(Au)>a当u∈P(θ,a,b)且‖Au‖>b, 则A至少存在三个不动点u1,u2与u3且满足 为了方便起见,我们令 (8) (9) 我们将函数Ψ,Φ,f所满足的条件罗列如下 (L1)f:[0,∞]→[0,∞]是一个非减连续函数。 (10) 引理7 假设条件(G1)和(G2)成立,T为(5)所定义的算子, 则有T:K→K。 证明由引理4与引理5及推论1知,若y(t)≥0,Ψ(y)≥0,Φ(y)≥0, 则 从而T(K)⊆K,即T:K→K. 定理2 假设条件(L1),(L2),(G1)和(G2)成立,并且存在四个数M,N,Q,P满足 (11) (12) 则对每一个 (13) 边值问题(1)-(3)至少存在三个与λ有关的正解y1(t),y2(t)与y3(t)满足 (14) 故得‖Ty‖ 即θ(Ty)>Q。 所以引理6中的条件(H1)成立。 最后, 我们验证引理6中的条件(H3)。 令y∈K(θ,Q,N)且满足‖Ty‖>N, 由式子(5)有 (15) 进而有 所以引理6中的条件(H3)成立。由引理6可以得到边值问题(1)-(3)至少有三个正解。 参考文献: [1] Atici F M,Eloe P W.Discrete Fractional Calculus with the Nabla Operator[J].ElectronJQualTheoryDiffer.(Equ.,Spec.Ed.I),2009,3:1-12.DOI: 10.14232/ejqtde.2009.4.3. [2] Atici F M,Eloe P W.Two-point Boundary Value Problems for Finite Fractional Difference Equations[J].JDifferenceEquAppl,2011,17(4):445-456.DOI: 10.1080/10236190903029241. [3] Goodrich C S.Solutions to a Discrete Right-focal Fractional Boundary Value Problem[J].IntJDifferenceEqu,2010,5(2):195-216. [4] Guo C J,O’Regan D,Xu Y T,etal.Existence and Multiplicityof Homoclinic Orbits of a Second-order Differential Difference Equation ViaVariational Methods[J].ApplMathInformMech,2012,4(1):1-15. [5] Bai D Y,Lian H R,Wang H Y.Exact Multiplicity of Solutions for Discrete Second Order Neumann Boundary Value Problems[J].BoundaryValueProblems,2015(1):229-17.DOI:10.1186/s13611-015-0495-1. [6] Guo C X,Guo J M,Kang S G,etal.Existence of Positive Solutions for Two Point Boundary Value Problems of Nonlinear Finite Discrete Fractional Differential Equations and Its Application[J].AdvancesinMathematicalPhysics,2016:1-9.DOI:10.1155/2016/7307614. [7] Yang J P.Sign-changing Solutions to DiscreteFourth-order Neumann Boundary Value Problems[J].AdvancesinDifferenceEquations,2013(1):1-11. [8] Zhong Q Y,Zhang X Q,Shao Z Y.Positive Solutions for Singular Higher-order Semipositone Fractional Differential Equations with Conjugate Type Integral Conditions[J].JNonlinearSciAppl,2017,10:4983-5001.DOI:10.22436/jnsa.010.09-37. [9] Liu X,Zhang Y B,Shi H P.Nonexistence and Existence Results for a Fourth-Orderp-Laplacian Discrete Mixed Boundary Value Problem[J].MediterrJMath,2015,12:419-432.DOI: 10.1007/s0009-014-0402-5. [10] Goodrich CS.Existence and Uniqueness of Sloutions to a Fractional Difference Equation with Nonlocal Conditions[J].ComputMathAppl,2011,61:191-202. [11] Bai Z B,Lv H S.Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation[J].MathAnalAppl,2005,311(1):495505.DOI: 10.1016/j.jmaa.2005.02.052. [12] Leggett R W,Williams L R.Multiple Positive Fixed Points of Nonlinear Operators on Ordered Banach Spaces[J].IndianaUniversityMathematicsJournal,1979,28(4):673-688.DOI:10.1512/jumj.1979.28.28046.1 准备知识
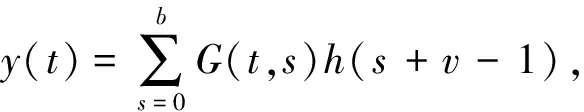
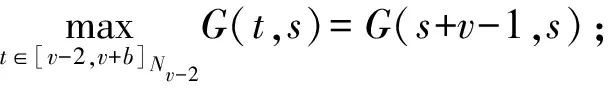
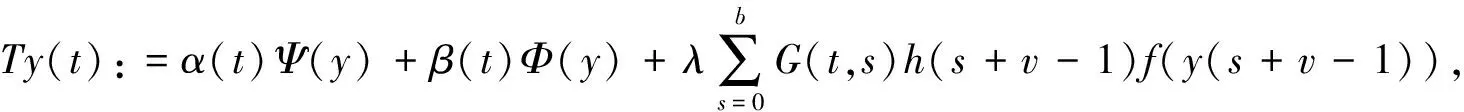
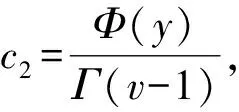
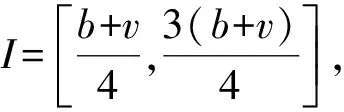
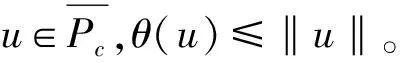
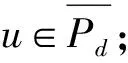
2 主要结果