异步切换与随机时延影响的切换系统网络化控制

池小波,常璐,贾新春

(山西大学 数学科学学院,山西 太原 030006)

0 引言

切换系统是由若干连续或离散的子系统和一组切换规则组成,这类系统可以描述实际工程中许多具有切换特性的混杂系统[1],例如电力系统和飞行交通系统等。另一方面,将通信网络引入到控制系统中导致信息在传输过程中发生网络诱导时延和数据丢包等现象,这使得网络化切换控制系统(NSCS)研究受到学者的广泛关注[2-5]。而且,信息的网络化传输会造成控制器模态切换时刻滞后于系统模态切换时刻,这称为异步切换现象[6]。例如,蜂窝移动通信中移动用户的通话质量受到多个用户与基站链路异步切换的影响,甚至可能导致通话失败[2]。因此,异步切换和切换间隔与采样数据执行间隔之间复杂的耦合关系是切换系统网络化控制研究的关键问题,还有待进一步研究。

近年来,网络化切换系统的控制研究主要分为三类:异步切换控制[7];带有网络化特征的同步切换控制[8];利用切换系统方法的网络化控制[9-10]。然而,同时考虑异步切换和网络诱导特征的NSCS的研究工作还是较少[11-12]。最近,文献[11-12]研究了切换时刻和采样时刻匹配的切换系统的网络化异步切换控制问题,但工程实际中网络化切换控制问题中的这种匹配现象几乎不存在。据作者所知,针对切换时刻和采样时刻不匹配情形下切换系统的网络化异步切换控制问题的研究工作还是较少[13]。然而文献[13]仅研究了控制输入执行区间与切换区间匹配情形下的网络化异步切换控制问题。针对离散时间切换系统,考虑切换时刻和采样时刻不匹配情形,本文建立带有异步切换与随机时延的离散时间NSCS模型。通过分段Lyapunov函数和平均驻留时间方法,得到闭环系统指数稳定的充分条件和网络化异步切换控制器的设计方法。

1 系统建模与问题描述

考虑一类离散时间切换线性系统∑:

x(k+1)=Aσ(k)x(k)+Bσ(k)u(k)

(1)

其中,x(k)∈Rn,u(k)∈Rm分别是状态向量和控制输入;xk0是系统的初始状态;σ(k):{k0,k0+1,…}→Λ={1,2,…,N}为切换信号,N>1为子系统个数。对于∀i∈Λ,Ai和Bi是适当维数的常矩阵。

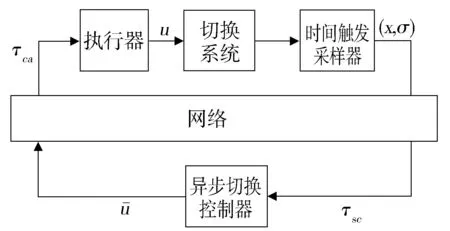
Fig.1 Structure of NSCS图1 NSCS结构图

本文的研究目标是同时考虑异步切换和随机时变时延,设计能够镇定系统∑的网络化异步控制器。所考虑的NSCS如图1所示。采样器具有检测和采集系统(1)的切换信号和状态的功能,采样数据的网络传输会产生网络诱导时延,并导致控制器异步切换。下面给出NSCS的假设:

假设1 采样器执行器都是时间驱动的,控制器是事件驱动的。h是采样周期。采样时刻和采样数据记为(kh,x(k),σ(k))。采样数据到控制器的传输时延记为τsc(k),产生的控制信号到执行器的传输时延记为τca(k)。

Fig.2 Process of data transmission in which thesampling instants are mismatched with switching instants图2 采样与切换时刻不匹配的数据传输过程

假设2 对于切换信号σ(k),有切换序列Υ={σ(k)|(σ(k0),k0h),…,(σ(ki),kih),…;i∈N}。当k∈[ki,ki+1)时,第σ(ki)个子系统被激活。切换间隔ki+1h-kih=nih,ni∈{3,4,…,n},n为常数。故切换时刻与采样时刻是不匹配的。

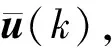
注1：通常网络化控制系统中假定采样数据到达控制器后立即驱动控制器生成控制信号,故假设1中控制器是事件驱动的[14]。

注2：考虑到离散系统的网络诱导时延一般为系统运行周期的整数倍,见图2。本文假定时延随机地取h,2h。为了研究切换信号和采样时刻不匹配的情形,仅考虑切换间隔大于网络诱导时延,故假设2中选取切换间隔最小为3h。另外,对于任意切换间隔与网络诱导时延问题的研究将是我们下一步工作。

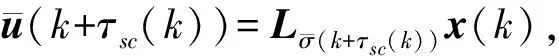
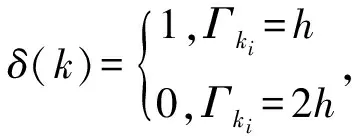
当k=ki时,u(k)=δ(k)Ljx(k-1)+[1-δ(k)]Ljx(k-2)

(2)

当k=ki+1时,u(k)=δ(k)Lix(k-1)+[1-δ(k)]Ljx(k-2)

(3)

当k=ki+λ时,λ=2,…,ni-1,u(k)=δ(k)Lix(k-1)+[1-δ(k)]Lix(k-2)

(4)

其中,Li,i∈Λ是控制器增益。

由系统(1)和控制器(2)-(4)可得,带有异步切换与随机时延的离散时间NSCS的模型为

x(k+1)=Aix(k)+δBiLjx(k-1)+Bi[1-δ]Ljx(k-2),k=ki

(5)

x(k+1)=Aix(k)+δBiLix(k-1)+Bi[1-δ]Ljx(k-2),k=ki+1

(6)

x(k+1)=Aix(k)+δBiLix(k-1)+Bi[1-δ]Lix(k-2),k=ki+λ,λ=2,…,ni-1

(7)

其中,x(k)=φ(k),k=k0,k0-1,k0-2,且φ(k0)=xk0

注3：与现存文献[11]异步切换控制系统模型相比较,本文建立了切换时刻与采样时刻不匹配的NSCS模型。在异步切换和切换间隔与采样数据执行间隔之间三重耦合的情形下,本文考虑Γk=h和Γk=2h两种时延情形,通过使用更一般的随机系统方法可以将其推广到多种时延的情形。

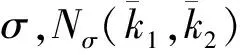
本文的控制设计问题是:在异步切换和切换间隔与采样数据执行间隔之间三重耦合的情形下,设计(2)-(4)的控制器增益Li和Lj,使得闭环系统(5)-(7)是指数稳定的。

2 主要结论

通过分段李亚普诺夫函数和平均驻留时间方法,本节首先给出系统(5)-(7)指数稳定性的充分条件,然后给出控制器(2)-(4)的设计方法。首先取候选Lyapunov函数为

V(xk)=Vχ(k)(k)=V1χ(k)(k)+V2χ(k)(k)+V3χ(k)(k)

(8)

其中,V1χ(k)(k)=xT(k)Pχ(k)x(k),V2χ(k)(k)=xT(k-1)Qχ(k)x(k-1)+(1+ρ(k))xT(k-2)Qχ(k)x(k-2)

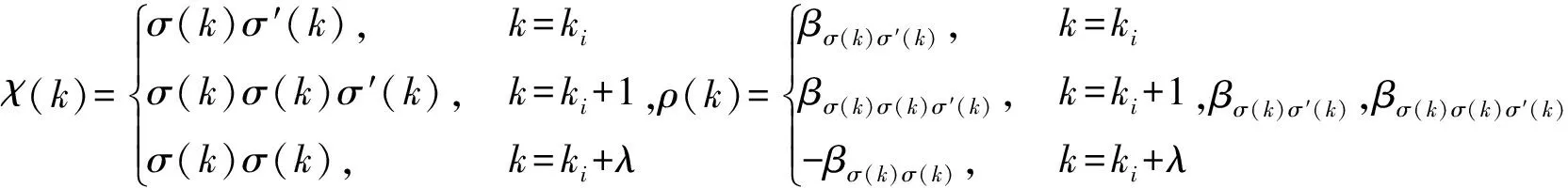
2.1 稳定性分析

定理1 考虑切换系统(5)-(7),给定正标量βij,βiij,βii∈(0,1),c<1,μ≥1和控制增益Li,i,j∈Λ,如果存在对称正定矩阵Pij,Piij,Pii,Qij,Qiij,Qii,Rij,Riij,Rii,使得对∀i,j∈Λ,i≠j下列不等式成立:

(9)

(10)

(11)

Pii≤μPiij,Piij≤μPij,Pij≤μPjj,Qii≤μQiij,(1+βiij)Qiij≤μQij,

(1+βij)Qij≤μQjj,Rii≤μRiij,(1+βiij)Riij≤μRij,(1+βij)Rij≤μRjj

(12)

其中,

Υ12=-2αRijBiLj+(1+βij)Rij,Υ13=2(α-1)RijBiLj,

Υ23=(1+βij)2Rij,Υ22=-(1+βij)(2+βij)Rij,

Υ33=-(1+βij)2(Rij+Qij),Υ44=-(Pij+2Rij)-1,

∏12=-2αRiijBiLi+(1+βiij)Riij,∏13=2(α-1)RiijBiLj,

∏23=(1+βiij)2Riij,∏22=-(1+βiij)(2+βiij)Riij,

∏33=-(1+βiij)2(Riij+Qiij),∏44=-(Piij+2Riij)-1,

∑12=-2αRiiBiLi+(1-βii)Rii,∑13=2(α-1)RiiBiLi,

∑23=(1-βii)2Rii,∑22=-(1-βii)(2-βii)Rii,

∑33=-(1-βii)2(Rii+Qii),∑44=-(Pii+2Rii)-1.

则对于任意满足下列平均驻留时间约束和异步时间比率约束的异步切换规则,系统(5)-(7)是指数稳定的

(13)

(14)

其中,βmin=min{βii|i∈Λ},βmax=max{βij,βiij|i,j∈Λ}。Tij(k0,k)和Tiij(k0,k)(或Tij和Tiij)分别表示双异步区间和单异步区间在(k0,k)上的激活时长。

证明针对k∈[ki,ki+1)将区间分成三部分:双异步区间k=ki,单异步区间k=ki+1和同步区间k∈[ki+2,ki+1)。下面首先分别研究这三类子切换系统的稳定性,然后总体分析闭环NSCS的稳定性。

情形1:当k=ki时,沿着系统(5)的轨迹计算Lyapunov函数(8)的前向差分。

E{ΔV1ij(k)|V1ij(k)}-βijV1ij=E{xT(k+1)Pijx(k+1)}-(1+βij)xT(k)Pijx(k)=

E{[Aix(k)+αBiLjx(k-1)+(1-α)BiLjx(k-2)+[δ(k)-α]BiLj(x(k-1)-x(k-2))]T×

Pij[Aix(k)+αBiLjx(k-1)+(1-α)BiLjx(k-2)+[δ(k)-α]BiLj(x(k-1)-x(k-2))]}-

(1+βij)xT(k)Pijx(k)=ξT(k)MijTPijMijξ(k)-(1+βij)xT(k)Pijx(k)+ξT(k)NijTPijNijξ(k)

(15)

其中,

E{ΔV2ij(k)|V2ij(k)}-βijV2ij=xT(k)Qijx(k)-(1+βij)2xT(k-2)Qijx(k-2)

(16)

E{ΔV3ij(k)|V3ij(k)}-βijV3ij=ξT(k)Λijξ(k)+2ξT(k)MijTRijMijξ(k)+2ξT(k)NijTRijNijξ(k)

(17)

其中,

Λ12=-2αRijBiLj+(1+βij)Rij,

Λ13=2(α-1)RijBiLj,Λ22=-(1+βij)(2+βij)Rij,

Λ23=(1+βij)2Rij,Λ33=-(1+βij)2Rij

由(9),(16)-(17)和Schur补引理得,E{Vij(k+1)|Vij(k)}-Vij(k)-βijVij=ξT(k)Υijξ(k)<0。即

Vij(ki+1)<(1+βij)Vij(ki)

(18)

情形2:当k=ki+1时,由(10)得:

Viij(ki+2)<(1+βiij)Viij(ki+1)

(19)

情形3:当k∈[ki+2,ki+1)时,即k=ki+λ,λ=2,…,ni-1,由(11)得:

Vii(k)<(1-βii)k-ki-2Vii(ki+2)

(20)

由(12)可知

Vii≤μViij,Viij≤μVij,Vij≤μVjj

(21)

结合(19)-(21),对于k∈[ki,ki+1),当k=ki+1时,忽略系数μ(1-βii)k-ki-2;当k=ki时,忽略系数μ2(1-βii)k-ki-2(1+βiij),故可得

Vii(k)≤(1-βii)k-ki-2Vii(ki+2)≤μ(1-βii)k-ki-2Viij(ki+2)≤

μ(1-βii)k-ki-2(1+βiij)Viij(ki+1)≤μ2(1-βii)k-ki-2(1+βiij)Vij(ki+1)≤

μ3(1-βii)k-ki-2(1+βiij)(1+βij)Vjj(ki)≤…≤

μ3Nσ(1-βmin)k-k0-Tij-Tiij(1+βmax)Tiij+TijV(k0)

(22)

又因(22)式中的平均驻留时间和异步率分别满足(13)和(14),故而

(23)

另一方面,由(8)易得:

(24)

其中,

2.2 控制器增益设计

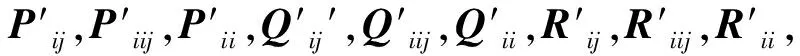
(25)

(26)

(27)

Pii′≤μPiij′,Piij′≤μPij′,Pij′≤μPjj′,

Qii′≤μQiij′,(1+βiij)Qiij′≤μQij′,(1+βij)Qij′≤μQjj′

(28)

其中,

Υ11′=∏11′=∑11′=-G-GT,Υ12′=-2AiG+Rij′,

Υ13′=-2αBiYj,Υ14′=-2(1-α)BiYj,Υ23′=(1+βij)Rij′,

Υ22′=-(1+βij)Pij′+Qij′+(1-βij-μij-1)Rij′,

Υ25′=GTAiT,Υ33′=-(1+βij)(2+βij)Rij′,Υ34′=(1+βij)2Rij′,

Υ35′=αYjTBiT,Υ45′=(1-α)YjTBiT,Υ55′=Pij′+2Rij′-G-GT,

∏12′=-2AiG+Riij′,∏13′=-2αBiYi,∏14′=-2(1-α)BiYj,

∏22′=-(1+βiij)Piij′+Qiij′+(1-βiij-μiij-1)Riij′,

∏23′=(1+βiij)Riij′,∏25′=GTAiT,∏45′=(1-α)YjTBiT,

∏33′=-(1+βiij)(2+βiij)Riij′,∏34′=(1+βiij)2Riij′,

∏35′=αYiTBiT,∏55′=Piij′+2Riij′-G-GT,∑12′=-2AiG+Rii′,

∑13′=-2αBiYi,∑14′=-2(1-α)BiYi,∑22′=-(1-βii)Pii′+Qii′+(1+βii-μii-1)Rii′,

∑23′=(1-βii)Rii′,∑25′=GTAiT,∑33′=-(1-βii)(2-βii)Rii′,

∑34′=(1-βii)2Rii′,∑35′=αYiTBiT,∑45′=(1-α)YiTBiT,

∑55′=Pii′+2Rii′-G-GT.

则对于任意满足(13)和(14)的异步切换规则,系统(5)-(7)是指数稳定的。进而控制器增益为Li=YiG-1.

证明记

Qiij′=GTQiijG,Qii′=GTQiiG,Rij′=GTRijG,Riij′=GTRiijG,Rii′=GTRiiG

利用[16]中引理2分离变量,再分别对(9)-(12)做合同变换。

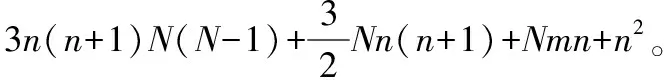
3仿真实例

考虑如下的离散时间线性切换系统[17]:

x(k+1)=Aσ(k)x(k)+Bσ(k)u(k)

(29)

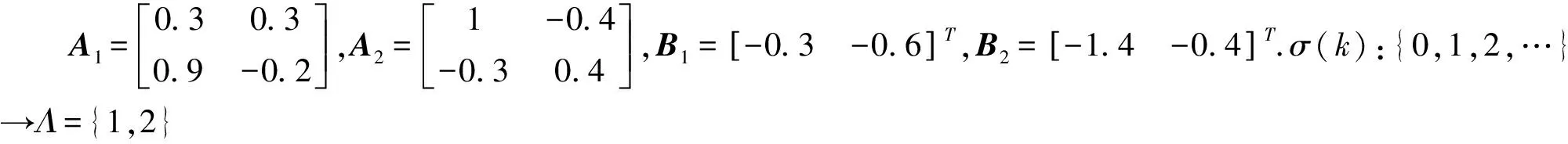
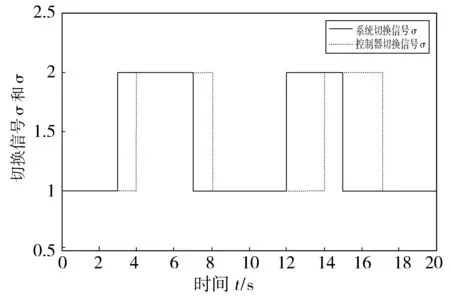
Fig.3 Switching signal图3 切换信号

Fig.4 State trajectories of the dosed-loop system图4 系统状态轨迹

4 结论

本文研究了切换时刻与采样时刻不匹配情形下带有两种时延的离散时间网络化异步切换控制设计问题。给出了闭环系统指数稳定的充分条件和一种网络化异步切换控制器的设计方法。针对多种时延情形以及切换间隔与传输时延更一般约束的情形下的网络化异步切换控制问题是我们未来的研究方向。

参考文献：

[1] Hai L，Antsaklis P J.Stability and Stabilizability of Switched Linear Systems:A Survey of Recent Results[J].IEEETransactionsonAutomaticControl，2009，54(2):308-322.DOI:10.1109/TAC.2008.2012009.

[2] 王月娥，吴保卫，汪锐.切换系统的异步镇定:相邻模型依赖平均驻留时间[J].物理学报，2015，64(5):58-64.DOI:10.7498/aps.64.050201.

[3] Ma D.Asynchronous Switching Network Protocol Design for Networked Linear Switched Systems[C]∥Proc.30th Chinese Control Conference，2011:4670-4675.

[4] Wen J，Peng L，Nguang S K.AsynchronousH∞Filtering of Switched Time-delay Systems with Network Induced Random Occurrences[J].SignalProcessing，2014，98(98):62-73.DOI:10.1016/j.sigpro.2013.11.002.

[5] Ma D，Liu J C.Robust Exponential Stabilization for Network-based Switched Control Systems[J].InternationalJournalofControlAutomation&Systems，2010，8(1):67-72.DOI:10.1007/s12555-010-0109-8.

[6] Zhang L X，Peng S.Stability，L2-gain and Asynchronous Control of Discrete-Time Switched Systems with Average Dwell Time[J].IEEETransactionsonAutomaticControl，2009，54(9):2192-2199.DOI:10.1109/TAC.2009.2026841.

[7] Wang Y E，Wu B W，Wu C.Stability andL2-Gain Analysis of Switched Input Delay Systems with Unstable Modes under Asynchronous Switching[J].JournaloftheFranklinInstitute，2017，354(11):4481-4497.DOI:10.1016/j.jfranklin.2017.04.006.

[8] 董朝阳，马奥家，王青，等.网络化切换控制系统故障检测与优化设计[J].控制与决策，2016(2):233-241.DOI:10.13195/j.kzyjc.2014.1838.

[9] Yu M，Wang L，Chu T，etal.Stabilization of Networked Control Systems with Data Packet Dropout and Network Delays Via Switching System Approach[J].EuropeanJournalofControl，2004，11(1):40-49.DOI:10.1109/CDC.2004.1429261.

[10] Zhang L，Gao H，Kaynak O.Network-Induced Constraints in Networked Control Systems-A Survey[J].IEEETransactionsonIndustrialInformatics，2012，9(1):403-416.DOI:10.1109/TII.2012.2219540.

[11] Ma D，Zhao J.Stabilization of Networked Switched Linear Systems:An Asynchronous Switching Delay System Approach?[J].Systems&ControlLetters，2015，77:46-54.DOI:10.1016/j.sysconle.2015.01.002.

[12] Chang L，Chi X B，Zhang L L，etal.Effects of Asynchronous Switching on Networked Control of A Class of Switched Systems[C]∥Proc.36th Chinese Control Conference，2017:8038-8043.DOI:10.23919/ChiCC.2017.8028628.

[13] Zhao X，Tian E，Wang L，Li H.Asynchronous Control for Discrete Switched Systems over Network by using Sojourn Probability Method[C]∥Proc.28th Chinese Control and Decision Conference，2016:962-967.DOI:10.1109/CCDC.2016.7531122.

[14] Jia X C，Chi X B，Han Q L，etal.Event-Triggered FuzzyH∞Control for a Class of Nonlinear Networked Control Systems Using the Deviation Bounds of Asynchronous Normalized Membership Functions[J].InformationSciences，2014，259:100-117.DOI:10.1016/j.ins.2013.08.055.

[15] Song Y，Fan J，Fei M，etal.RobustH∞Control of Discrete Switched System with Time Delay[J].AppliedMathematics&Computation，2008，205(1):159-169.DOI:10.1016/j.amc.2008.05.046.

[16] Wu H N.Reliable RobustH∞Fuzzy Control for Uncertain Nonlinear Systems With Markovian Jumping Actuator Faults[J].JournalofDynamicSystemsMeasurement&Control，2007，129(3):252-261.DOI:10.1105/1.2718236.

[17] 牟春伟.离散切换系统的异步H∞控制和滤波[D].大连:大连理工大学，2013.