冲击波作用下单层钢化玻璃应变阈值的数值模拟*
2018-05-21刘俊,田宙,钟巍,3
刘 俊,田 宙,钟 巍,3
(1.湘潭大学材料科学与工程学院,湖南 湘潭 411100;2.西北核技术研究所, 陕西 西安 710024;3.北京大学数学科学学院, 北京 100871)
随着经济的发展和人们生活水平的提高,人们在结构装饰方面越来越重视外观的设计。钢化玻璃具有良好的透光性、隔音效果以及自重轻、易安装的优点,已经渐渐与建筑融合在一起,成为建筑不可或缺的一部分。尤其对于现代高层建筑[1]来说,钢化玻璃已经替代传统的结构材料作为建筑幕墙使用,是现代建筑玻璃幕墙采用的最广泛的玻璃之一。钢化玻璃也被广泛应用于汽车、火车、轮船、飞机等其他领域。
近年来,偶然爆炸和事故爆炸事件越来越多:例如美国德克萨斯州韦科市附近的一家化肥厂因存储硝酸铵不当引发剧烈爆炸;我国天津港因为危化品放置不当发生爆炸事件;昆明一家餐馆在置换燃气时因操作不当发生燃气爆炸。另外,针对公共建筑的恐怖爆炸袭击事件也时有发生。钢化玻璃在爆炸冲击波作用下易于破碎,在爆炸冲击波或者自身重力作用下对人和物会产生重大的损伤。因此,对于单层钢化玻璃破坏的应变阈值的研究是非常必要的,钢化玻璃是一种预应力玻璃,其弯曲强度和抗冲击性能都要优于普通玻璃。钢化玻璃是一种典型的脆性材料,但其破坏形式不完全与脆性材料的破坏相同[2],因此钢化玻璃的破坏是一个比较复杂的过程。
随着数值模拟技术的不断发展,数值模拟成为爆炸冲击波对结构响应领域研究的一种重要手段。近年来用数值模拟方法对钢化玻璃的研究取得了一定的成果。李磊等[3]采用改进SHPB实验方法对钢化玻璃的动态力学性能进行了研究,运用ANSYS/LS-DYNA模拟了材料的应力时程关系,得出的Johnson-Cook模型可以很好地模拟钢化玻璃的本构关系。Pyttel等[4]提出了一种最小能量失效准则,裂纹的形成和长大采用局部最大应力准则,并利用有限元软件进行模拟,说明了这种失效准则的有效性。上述研究中,对单层钢化玻璃在冲击波作用下破坏的研究还很少,对单层钢化玻璃的失效准则选用的大多都是应力相关准则。
本文中,借助ANSYS/LS-DYNA程序,建立单层钢化玻璃在爆炸冲击波作用下的有限元模型。对实验测得的爆炸冲击波载荷进行合理简化,加入侵蚀算法来模拟钢化玻璃破坏裂纹扩展,钢化玻璃破坏准则选用最大伸长线应变。通过大量的计算,得到单层钢化玻璃破坏的一个定量应变阈值,并与实验进行对比,证明得到的应变阈值是合理的。在模拟单层钢化玻璃在冲击波作用下的响应问题时,可作重要参考。
1 数值模拟
选用ANSYS/LS-DYNA软件[5-6]来进行冲击波对钢化玻璃作用过程的有限元模型的建立和计算,在LS-PREPOST3.0进行计算后处理。
1.1 有限元模型
在ANSYS/LS-DYNA平台上,建立钢化玻璃板的数值模型。钢化玻璃的尺寸为1 300 mm×1 600 mm×10 mm,采用3D SOLID 164八节点实体单元。用Lagrange单元[7]描述钢化玻璃,对建立模型进行合理网格划分,对钢化玻璃板施加合适的边界条件和加载条件。
1.2 载荷简化
空气冲击波传播过程中波阵面压力在初始阶段衰减很快,后期衰减平缓,典型的爆炸冲击波超压[8-9]随时间变化曲线如图1所示。冲击波超压随时间变化的经验公式可描述为:
p(t)=p0(1-t/td)e-at/td
(1)
式中:p(t)为某时刻瞬间超压;p0=pm-pa,为峰值超压,pa为大气压,pm为最大压力值;a为衰减系数;td为正压作用时间。
为了得到钢化玻璃破坏时的应变阈值,需要大量的计算。对于结构来说,爆炸正压段引起大部分破坏,所以主要的爆炸参数为正压段的超压和冲量。因此,在这里对爆炸冲击波载荷进行简化[10],将实验测得的压力载荷简化为三角形载荷。压力峰值取曲线的最大值;压力作用时间t=2I/pmax,I为积分所得冲量,pmax为峰值超压,t为超压作用时间。简化后的爆炸冲击波载荷时程曲线如图2所示。
1.3 材料模型
钢化玻璃采用线弹性材料模型[11],参照文献[12],钢化玻璃材料参数分别为:ρ=0.002 5 g/mm3,E=72 GPa,ν=0.23。计算中通过侵蚀算法实现钢化玻璃失效准则的定义。钢化玻璃单元达到破坏条件后,把失效单元从模型中删除,从而得到钢化玻璃裂纹扩展情况。
1.4 边界条件
对钢化玻璃板采用框架支撑的固定方式,为了尽可能保证数值模型中对钢化玻璃的约束与实际应用条件相同,这里对钢化玻璃数值模型采用四周局部约束边界条件,模拟钢化玻璃被固定在钢框架上 。
1.5 网格敏感性
爆炸冲击波对钢化玻璃作用会受到钢化玻璃板网格划分的影响[13],单元网格尺寸不同,会对计算结果造成差异,网格尺寸大小对计算机的计算时间也有较大影响。为了降低网格尺寸对结果的影响,对网格敏感性进行了研究。保证其他计算条件不变,只改变网格尺寸大小进行一系列计算,得到网格尺寸对计算结果和计算机计算时间关系,如图3~4所示。由图3可以看出,随着网格的减小,钢化玻璃板中心位移逐渐增大,但增加的幅度越来越小,逐渐趋于稳定,其中网格尺寸为5 mm和网格尺寸为10 mm的计算结果仅相差0.7%;但是由图4可以看出,网格尺寸为10 mm的计算时间是网格尺寸为5 mm的计算时间的5倍。因此,综合考虑了模拟结果精度和计算时间的合理性,本文中玻璃厚度方向划分3个网格,长度方向和宽度方向的网格尺寸都为10 mm。
2 实 验
进行了一系列的实验研究,实验工况条件与数值模型相对应,对于相同规格的钢化玻璃(指厚度、尺寸、加工条件、材料性质等均相同),通过调整爆炸装药与钢化玻璃之间的距离进行多次实验,获得不同冲击波条件下的实验结果,得到该规格玻璃的冲击波毁伤规律以及毁伤阈值范围。
本次实验单层钢化玻璃尺寸为1 600 mm×1 300 mm×10 mm。 每次实验分别布置 PCB和自由场两个压力传感器、一个高速摄影相机、两个压力传感器,分别测量玻璃板中心的压力和与爆心距等距离的自由场压力,高速摄影相机可以看到玻璃板的破坏过程,实验布局如图5所示。
共进行了9发实验,其中处于阈值范围之内的有2发,测得结果及钢化玻璃破坏状态,见表1。通过对实验结果分析,本次实验中10 mm厚的钢化玻璃的冲击波毁伤阈值分别约为69 kPa和189 kPa·ms。
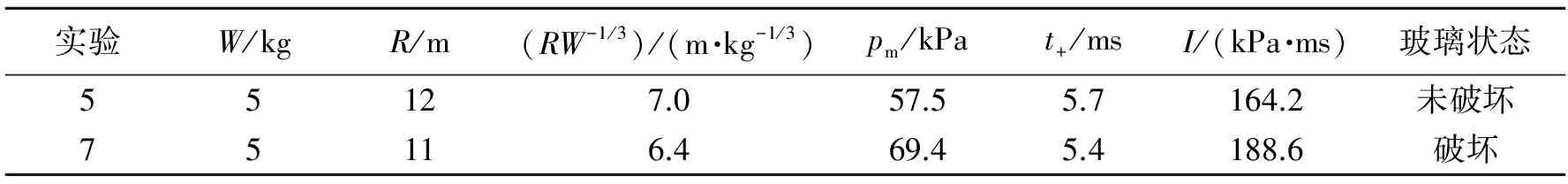
表1 实验结果Table 1 Experiment results
3 数值模拟与实验结果对比
为了得到钢化玻璃破坏的应变阈值,需要将计算结果与钢化玻璃实验阈值进行比对,因此这里把计算结果与第5、7发实验进行对比。计算超压和冲量分别对应第5发和第7发实验结果,在保证其他参数不变的情况下,应变阈值分别取值0.000 5、0.001、0.002、0.003进行计算,计算结果见表2,玻璃破坏情况如图6~7所示。由于计算模型中采用的是侵蚀算法,通过对失效材料单元的删除来实现钢化玻璃裂纹扩展,因此模拟计算中的钢化玻璃的破坏形态与实验结果会有一定差异。但钢化玻璃在此条件下破坏与否,两者反映的结果是一致的。

表2 不同应变阈值下模拟结果与实验结果对比Table 2 Comparison of simulation results at different strain thresholds with experiments
由图6可以看到,第5发实验钢化玻璃没有被冲击波打碎。而数值模拟5中:当应变阈值为0.003时,钢化玻璃没有破坏,与实验结果一致;当应变阈值为0.002时,模拟钢化玻璃板出现裂纹,即代表钢化玻璃破坏,与实验结果不一致;当应变阈值小于0.002时,钢化玻璃都发生破坏,明显与实验结果不一致。由图7可以看到,第7发实验钢化玻璃被冲击波打碎。而数值模拟7中:当应变阈值为0.003时,钢化玻璃没有破坏,与实验结果不一致;当应变阈值为0.002时,模拟钢化玻璃板破坏,与实验结果一致;当应变阈值大于0.003时,钢化玻璃不会破坏,与实验结果不相符。通过上面不同应变阈值的计算结果与实验结果对比可得,单层钢化玻璃的应变阈值在0.002和0.003之间。

表3 不同应变阈值下模拟结果与实验结果对比Table 3 Comparison of simulation results at different strain thresholds with experiments
为了得到更加精确的应变阈值,在0.002和0.003范围之间取值0.002 2、0.002 4、0.002 6、0.002 8作为单层钢化玻璃的应变阈值进行计算。并与第5发和第7发实验结果进行比对,见表3。
由表3可以看出,通过对单层钢化玻璃破坏实验与数值模拟结果对比,当应变阈值为0.002 2时,计算结果与实验5、7结果吻合一致。为了进一步验证应变阈值为0.002 2时计算结果的合理性,又将应变阈值为0.002 2的计算结果与场地实验5、7的高速摄影结果进行比对,如图8~9所示。第5发实验的高速摄影显示钢化玻璃整个过程没有破坏,模拟计算结果在整个过程中也没有破坏,第7发实验高速摄影显示钢化玻璃在中间位置开始发生破坏,然后波及整个钢化玻璃板,实验中钢化玻璃的破坏位置和数值模拟中破坏位置大致相同。由于场地实验周围环境比较复杂,计算超压冲量与实验测得的超压冲量误差可以忽略不计。由此可得,在可接受的超压和冲量误差范围内,单层钢化玻璃尺寸为1 300 mm×1 600 mm×10 mm、四边采用框架支撑方式,当应变阈值为0.002 2时,实验结果和计算结果是一致的,因此单层钢化玻璃的应变阈值为0.002 2是合理的,可以作为计算参数对单层钢化玻璃在冲击波作用下的数值模拟算例进行计算。
4 总 结
(1)数值模拟结果和实验结果基本一致,说明本文建立的数值计算模型和方法符合实际情况。
(2)通过大量的数值计算,不断地调节钢化玻璃应变阈值参数,得到了单层钢化玻璃尺寸1 300 mm×1 600 mm×10 mm、四边采用框架支撑方式,在冲击波作用下破坏的应变阈值为0.002 2。与实验结果进行对比,证明此结果是合理的,可以作为计算参数对单层钢化玻璃的数值模拟进行计算。
(3)由于本文中只对一种尺寸的单层钢化玻璃进行模拟计算,考虑到不同尺寸的单层钢化玻璃,其性能存在差异,因此本文结果对其他与本文尺寸相差较大的钢化玻璃是否合适,需要继续研究。
参考文献:
[1] 何建辉.钢化玻璃在建筑上的应用[J].玻璃,2012,39(12):46-49.
HE Jianhui. Application of thermal tempered glass on bulidings[J]. Glass, 2012,39(12):46-49.
[2] 李磊,安二峰,杨军.钢化玻璃应变率相关的动态本构关系[C]∥第七届中国功能材料及其应用学术会议论文集.长沙,2010.
[3] 李磊,安二峰,杨军.典型建筑玻璃力学性能的SHPB实验[J].硅酸盐通报,2010,29(2):390-394.
LI Lei, AN Erfeng, YANG Jun. Impact properties of typical architectural glass by SHPB[J]. Bulletin of the Chinese Ceramic Society, 2010,29(2):390-394.
[4] PYTTEL T, LIEBERTZ H, CAI J. Failure criterion for laminated glass under impact loading and its application in finite element simulation[J]. International Journal of Impact Engineering, 2011,38(4):252-263.
[5] 赵海鸥.LS-DYNA动力分析指南[M].北京:兵器工业出版社,2003.
[6] 张红松.ANSYS14.5/LS DYNA非线性有限元分析实例指导教程[M].北京:机械工业出版社,2013.
[7] LS-DYNA theoretical manual[Z]. California: Livermore Software Technology Corporation, 2001.
[8] 葛杰,李国强.建筑夹层玻璃在冲击荷载下的破坏研究概述[J].结构工程师,2010,26(4):137-143.
GE Jie, LI Guoqiang. A review of research on the failure of architectural laminated glazing under explosive loads[J]. Structural Engineers, 2010,26(4):137-143.
[9] 段雷琳,高轩能.爆炸冲击荷载下玻璃幕墙建筑抗爆研究[J].低温建筑技术,2012,34(5):41-43.
DUAN Leilin, GAO Xuanneng. Study on blast resistant for glassing curtain wall construction under blast loading[J]. Low Temperature Architecture Technology, 2012,34(5):41-43.
[10] 张其林,陶志雄,王勋,等.爆炸作用下夹层玻璃幕墙动力响应试验研究[J].建筑结构学报,2013,34(4):74-80.
ZHANG Qilin, TAO Zhixiong, WANG Xun, et al. Dynamic response research of laminated glass curtain wall subjected to blast loading[J]. Journalof Building Structures, 2013,34(4):74-80.
[11] 赵西安.JGJ 102-2003《玻璃幕墙工程技术规范》设计部分介绍[J].建筑科学,2004,20(3):1-7.
ZHAO Xi’an. Design part in technical specification of glass curtain wall engineering[J]. Building Science, 2004,20(3):1-7.
[12] HIDALLANA-GAMAGE H, THAMBIRATNAM D, PERERA N. Influence of interlayer properties on the blast performance of laminated glass panels[J]. Construction and Building Materials, 2015,98:502-518.
[13] 石磊,杜修力,樊鑫.爆炸冲击波数值计算网格划分方法研究[J].北京工业大学学报,2010,36(11):1465-1470.
SHI Lei, DU Xiuli, FAN Xin. A study on the mesh generation method for numeical simulation of blast wave[J]. Beijing University of Technology, 2010,36(11):1465-1470.
