高超声速飞行器时间协同再入制导

方科，张庆振，倪昆，程林，黄云涛

1.北京航空航天大学 自动化科学与电气工程学院，北京 100083 2. 北京航天自动控制研究所，北京 100076

以无动力高超声速再入飞行器为代表的远程作战武器具有作战范围广、飞行速度快、跟踪难度大、作战效能高等特点[1]，在近些年来受到各国越来越多的关注。与此同时，各国相继研发了近迫武器系统(CIWS)、“宙斯盾”等一系列反导系统[2]，使得其作战效能与突防能力大幅下降。在此背景下，相对于传统提高单兵作战效能的方法，发展多飞行器协同饱和打击更加符合未来战场作战需要，其个体之间通过功能互补可以实现饱和攻击、协同抗干扰等复杂功能。

高超声速飞行器的远距离飞行和复杂不确定性环境特点，使得飞行时间具有较大波动，难以实现在同一时刻对目标进行饱和打击的任务需求。其中再入飞行段占据了90%以上的飞行时间，是决定最终饱和打击效果的关键因素之一。因而发展多高超声速飞行器协同再入制导技术是未来协同体系作战的必要条件之一。

本文以多高超声速飞行器协同饱和打击为应用背景[3-5]，将其飞行过程分为初始发射段、协同再入段和协同末制导段。其中初始发射段通过程序发射序列确保协同再入的可行性；协同末制导段由文献[5-9]实现。而在这之间的协同再入段占据了整个飞行过程中的绝大多数时间与路程，在传统单飞行器高精度、高可靠性的再入制导律基础上，要求多飞行器能在同一时刻到达指定的中末交班地点。协同再入飞行[3,10]作为近两年来的新型任务需求，针对其协同制导结构与制导律的设计，现有文献均鲜有涉及。

单个高超声速飞行器的再入制导是一个复杂的多约束轨迹规划问题，现阶段主要有“标称轨迹法”和“预测-校正法”[11-14]。前者离线生成标准弹道并在实际再入过程中进行轨迹跟踪，简单易行但自主性和精度较差。后者在弹道预测的基础上进行轨迹校正，自主性与精度较高，但实时性较差且在线约束管理能力较弱[11-12]。

多弹协同制导技术不同于多无人机[15-16]和多机器人[17-18]的协同控制，其运动速度快、运动方向单一、能量耗散过程不可逆等特点[6,19]使得多无人机的协同控制方法无法直接使用。林涛等[19]首先对多弹协同的基本问题进行阐述；2006年，Jeon等[5]实现指定飞行时间的最优末导引律设计。赵世钰和周锐[6-7]结合协调变量[8]提出双层协同制导架构；2009年，张友安等[9]提出“领弹-从弹”的协同制导架构。后续的研究工作大部分是针对这两套架构的拓展与完善，并且主要集中于末制导律的设计上。

高超声速飞行器时间协同再入制导将以上两个技术相结合的同时，也催生出其特有的难点：

1) 时间协同再入飞行对再入制导律的实时性、在线约束管理等方面提出更高的要求，需要对现有方法加以优化。

2) 现有再入制导律并没有考虑飞行时间约束，飞行过程中的参数摄动使得再入时间不可知且不可控，难以满足协同再入飞行的时间一致性要求。因而需要将时间约束加入到制导律的设计之中，解决再入时间的不可预知性和不可控性。

3) 高超声速飞行器相对于传统导弹，其飞行速度更快、再入过程更为复杂、控制变量较为单一，并且无动力的再入飞行特点使得总能量有限且控制过程不可逆，无法直接将例如文献[6]中的双层协同结构运用于协同再入制导中，因而需要在协同结构和协调策略上进行改进和创新。

本文首先对现有单个飞行器的制导律加以改进，提升其实时性、在线约束管理能力以满足协同再入制导任务需要；进而针对再入飞行时间可知性与可控性问题，提出时间可控再入制导律；最后根据协同再入任务背景需求，基于多飞行器时间协调信息提出协同再入制导结构和协调策略，实现多高超声速飞行器的时间协同再入飞行过程。

1 协同再入问题描述

在不考虑地球自转的情况下，多个无动力高超声速飞行器三自由度运动方程为

(1)

式中：下标i代表第i个飞行器；v为其相对于地球的速度；r为飞行器到地球中心的距离；λ和φ为地球经纬度；Se为射程角；θ为速度倾角，向上为正；ψ为速度偏航角，以正北顺时针为正；σ为倾侧角，右偏为正；m为飞行器质量；g为地球重力加速度；L和D为升力和阻力。

(2)

(3)

(4)

(5)

再入过程中终端约束与控制约束如式(6)～式(8)所示:

h(tf,i)=hf,i，v(tf,i)=vf,i

(6)

λ(tf,i)=λf,i，φ(tf,i)=φf,i

(7)

(8)

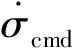
针对终端时刻一致的协同再入过程，给出整个飞行过程的时间约束如式(9)所示:

tf，1=tf，2=…=tf, n

(9)

式中：tf,i为第i个飞行器的终端时刻。

仿真对象为CAV-H，相关参数详见文献[20-21]。由文献[20]可知再入过程中采用的固定攻角剖面为

(10)

2 协同结构与制导方案

2.1 协同结构

多高超声速飞行器协同再入的核心任务是在同一时刻到达指定交班点。结合文献[6]与协同再入背景，设计协同再入制导架构如图1所示。其中再入过程分为初始下滑段、平衡滑翔段和再入终段[14]。

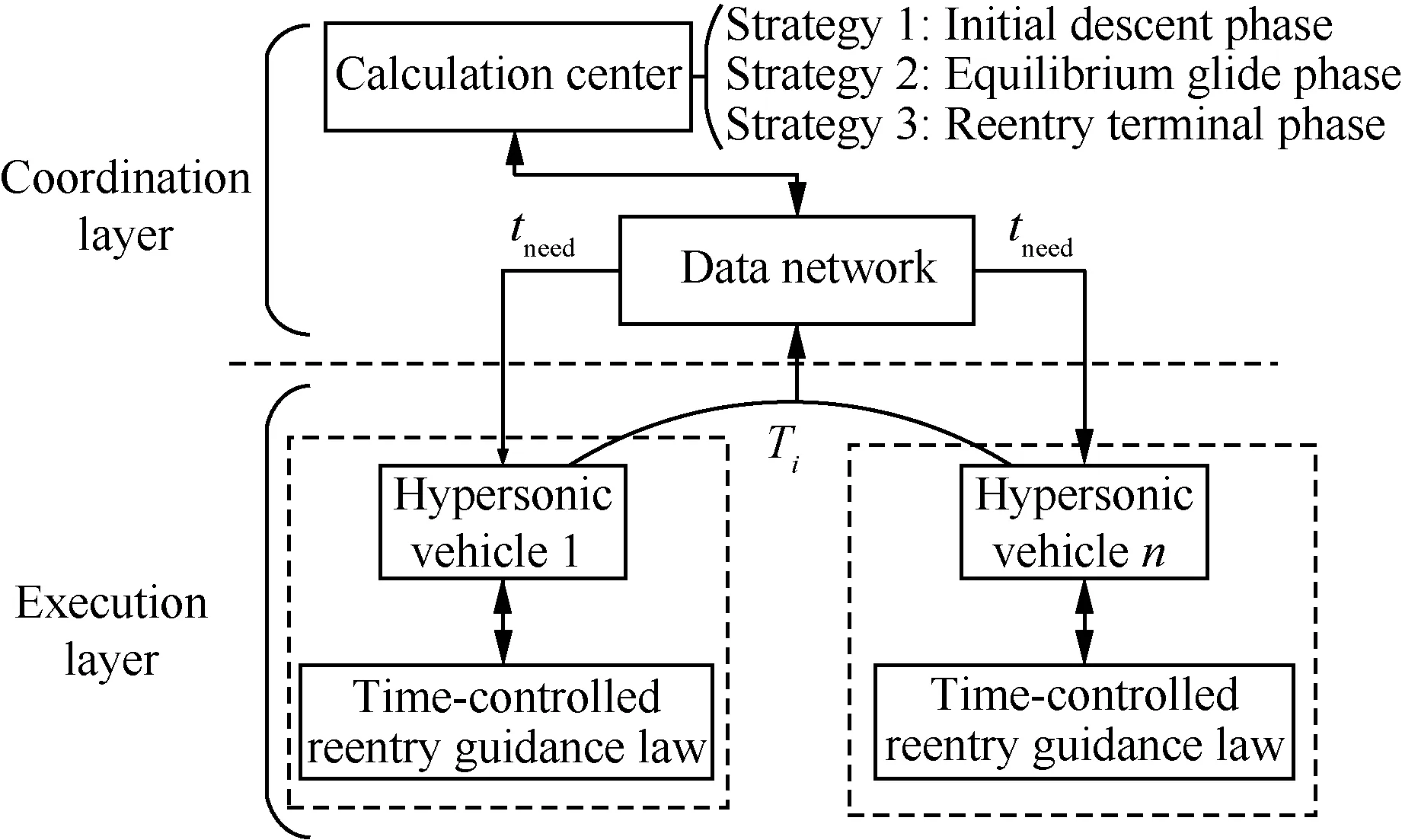
图1 协同再入制导架构Fig.1 Architecture of cooperative reentry guidance

整个协同结构分为两层，上层为协调层，适用于分布式/集中式的通讯结构，生成时间协调信息[8]；下层为执行层，由时间可控再入制导律进行在线轨迹预测与校正。

本文以集中式的通讯结构为例进行相关结构的设计。多个飞行器通过中继卫星等外部设备，将各自的预估飞行时间Ti传给集中运算单元。运算单元根据协调策略计算时间协调信息tneed，并将其传回至各飞行器，各飞行器以时间协调信息为约束进行在线轨迹设计。不同再入飞行阶段的协调策略各不相同，具体见本文3.3.3节。

2.2 时间可控再入制导方案

时间可控再入制导总体方案如图2所示,主要包括轨迹预测-校正、在线约束管理和再入飞行时间预估-校正3个模块。图中：α为功角；σd为轨迹规划模块求得的倾侧角;σcmd为指定的倾侧角。

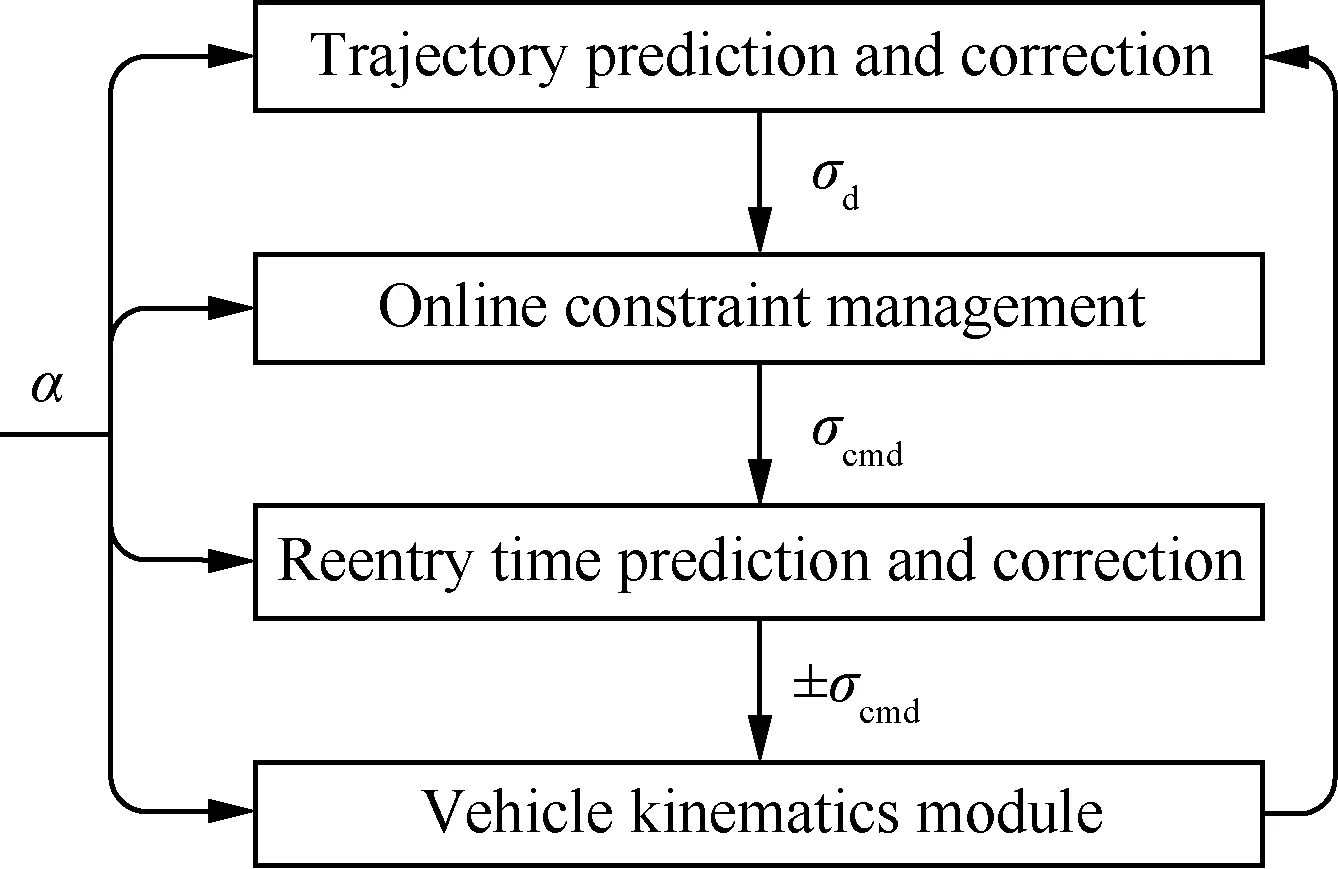
图2 总体制导方案Fig.2 Overall scheme of reentry guidance

首先,轨迹预测与校正模块在理论推导的基础上进行控制剖面参数化，在满足约束的前提下将原本复杂的轨迹规划问题转换为单参数的规划，通过在线倾侧角剖面调整信息的收集与预测，利用一次轨迹积分完成倾侧角剖面的调整，减少制导周期内的冗余计算并提高实时性。其次,在线约束强化管理模块引入控制理论的相关方法，实现对过程约束、终端约束和控制约束的在线强化管理，在不需要前期大量参数试凑的前提下提高制导律的在线约束管理能力。最后，时间预估-校正模块在时间敏感性分析的基础上，将视线角走廊作为控制变量，采用神经网络和Gauss-Newton迭代法实现基于时间误差的视线角走廊动态调整策略，实现指定时间的再入飞行。

3 时间可控再入制导律

3.1 轨迹预测-校正

3.1.1 控制剖面参数化

再入过程是一个复杂的多约束规划问题，传统方法通过人为设定规划点以达到在线求解的目的，限制了飞行器的能力，难以满足协同再入任务自主性要求，因而需要进行改进。首先构建图 3所示的高度-速度(H-V)走廊和如图 4所示的复合倾侧角走廊，具体流程见文献[11]。

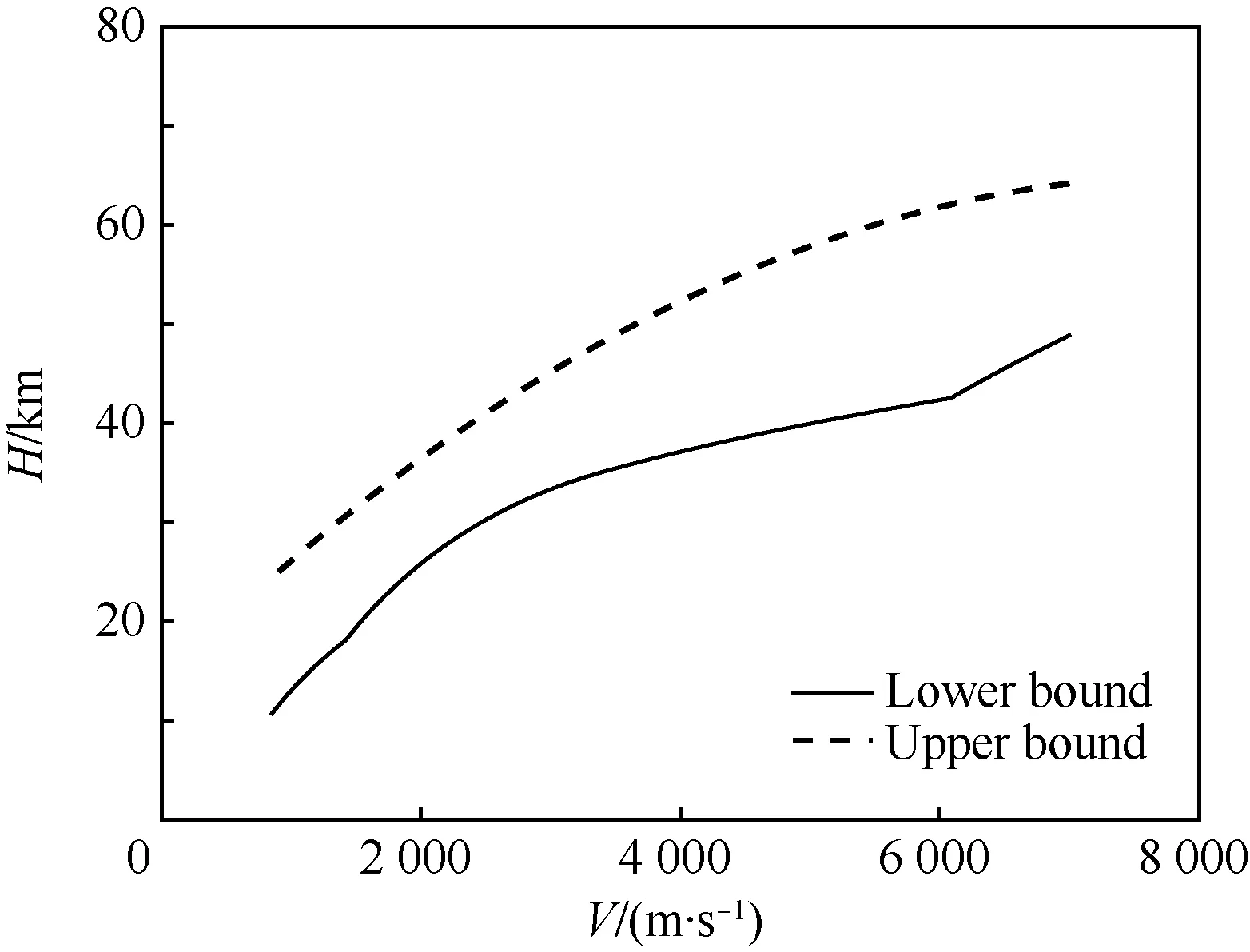
图3 高度-速度走廊Fig.3 Altitude-velocity corridor

图4 复合倾侧角走廊Fig.4 Compound bank angle corridor

终端经纬度约束可转化为如式(11)所示的射程约束：

(11)

将式(1)中的射程角对速度求导可得

(12)

式中：CD为阻力系数；Sref为参考气动面积。

联立式(11)和式(12)可以定性的得出以下结论：一定速度下，|dSe/dv|关于高度h的增加而单调递减；结合拟平衡滑翔假设[11]可进一步得到推论，随着倾侧角的增大，|dSe/dv|增大，飞行器滑翔能力和飞行距离减小；反而反之[14]。

再入轨迹规划本质上是多约束条件下的非线性规划问题。在上述推导的基础上进行控制剖面参数化，将倾侧角走廊上下界进行加权得到规划的倾侧角剖面。

σd(v)=ωσmin(v)+(1-ω)σmax(v)

(13)

式中：σd(v)为某速度下规划的倾侧角；σmin(v)和σmax(v)分别为某速度下倾侧角走廊上下界；ω为权重系数。不同权重下的射程规划能力如图 5所示。

通过控制剖面参数化，在满足过程约束、终端约束的基础上，将再入过程中的射程约束转化为权重系数ω的单参数规划问题，并且二者呈如图5所示的单调递增关系，降低了问题求解难度和提高了射程规划能力。

图5 权重系数-射程Fig.5 Weight coefficient-range

3.1.2 跨周期轨迹预测-校正

传统预测-校正制导方法在每个周期内通过多次的轨迹积分来获取必要的参数调整信息，造成大量冗余计算和规划周期不稳定情况出现[14]，难以满足协同再入要求。由于多个制导周期之间的控制剖面调整信息存在一定的连续递推关系，因而采用校正信息在线收集与预测方法，将这部分递推信息进行有效的收集与模型辨识。由图 5的单调性可知，规划射程与权重系数可在小范围内近似成式(14)的一阶线性函数关系:

Spre(ω)≈aω+b

(14)

式中：Spre为规划射程；a、b为待估计参数。通过前k个周期的剖面调整收集，得到的观测模型为

Hkx+Ek=Zk

(15)

为达到最优的参数估计结果，最小化式(16)性能评价指标:

(16)

式中：正定阵Qk为权重矩阵。利用前k个周期的剖面调整与预测信息，对第k+1个周期的权重系数进行估计，其中加权矩阵迭代设置为

(17)

最终估计参数表达式为

(18)

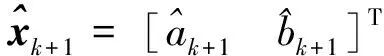
(19)

通过式(18)和式(19)，将原本隐函数关系的权重-射程函数式(14)进行了显式的递推表达。因而在整个制导过程中，利用式(19)对前k个周期剖面调整与预测信息的观测，递推出如式(18)所示的第k+1个周期的估计参数，进而直接求解出第k+1个周期的剖面调整信息，即

零工经济(Gig Economy)中的零工(Gig)原意是指临时工，是一些劳动者无法获得正式工作，只能从事一些临时性工作[1]。由于产业的周期性以及季节的周期性，有些工作并长期不雇佣劳动力，往往是需要的时候才雇佣工人，此时就会出现大量劳动力以团队形式暂时的集聚于某一地方或某一产业的现象，例如农民工[2,3]。由这种临时工所形成的经济现象被称为零工经济。改革开放以来，我国的很多城市中都出现过这种“零工”现象。

Spre(ω)=Sgo

(20)

(21)

式中：Sgo为所需的剩余射程。

通过在线的参数收集与递推，在每个制导周期内仅需要一次轨迹积分即可完成倾侧角剖面的调整，大大提高了在线轨迹规划效率，满足协同再入制导的在线轨迹规划实时性要求。

3.2 在线约束强化管理

轨迹预测-校正为再入过程提供可行的纵向轨迹，但实际飞行中再入轨迹仍然存在违反约束的情况[11,14]，因而需要对其进行在线约束强化管理，提高制导律的可靠性与稳定性。具体流程如图6所示，其中约束管理对象包括过程约束、终端约束和控制约束。图中：σco为修正的倾侧角指令；σpo为滤波前的倾侧角指令。

图6 在线约束管理Fig.6 Online constraint management

3.2.1 过程约束管理

由式(2)～式(4)可知，再入过程中的热流、动压、过载约束可以转化为H-V走廊下界，并且存在唯一的高度-速度对应关系。引入剩余高度:

Δhd=h-hdown>0

(22)

式中：hdown为当前速度下H-V走廊下界高度。

为保证飞行高度总是在走廊下界之上，对高度求导并设计如式(23)所示的高度下降速率限制器为

(23)

式中：λh为高度趋近系数。

当飞行器存在超过下界趋势时，该模块将倾侧角限制到合理的范围之内，而这其中产生的射程误差又能在后续的制导周期中得到补偿，因而不会影响整个再入过程的精度。同时，其计算量极小且校正过程基于当前高度信息因而不需要前期的参数试凑，具有较高的约束管理可靠性。

3.2.2 终端约束管理

再入过程还需要满足如式(6)的终端高度与速度约束。对式(1)中的高度与速度倾角在拟平衡滑翔条件的平衡点(h,θ)处小扰动线性化可得

(24)

式中：

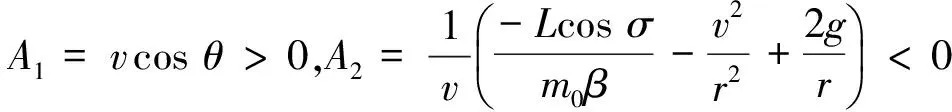
(25)

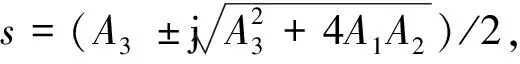
σco=arccos(cosσd+Δcosσ)

(26)

3.2.3 控制约束管理

规划的倾侧角剖面在实际执行过程中受限于式(9)执行速率，需要加入的指令滤波环节为

(27)

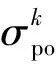
通过以上3种约束强化算法的设计，在不影响实时性的前提下，提高再入制导律的在线约束管理能力，为之后的协同过程提供实时可靠的纵向轨迹支持。

3.3 再入时间预估-校正

3.3.1 视线角走廊设计

一套完整的再入制导律还需要横向上的倾侧角符号规划。本文在传统的三段式视线角(Line of Sight，LOS)走廊的基础上进行时间可控制导律设计。反转逻辑如式(28)所示，走廊如图7所示。

(28)

式中：Δψup和Δψdown分别为当前速度下的视线角走廊的上下界。视线角走廊根据CAV-H的再入任务[20]进行设置，v0～v4分别为视线角走廊转折点速度，初始速度v0=7 000 m/s，初始下滑段走

图7 视线角走廊Fig.7 Line of sight (LOS) corridor

廊上限为5°；终端速度v4=800 m/s，走廊上限为2°；中间段上限为x。

通过对中间段x的调整，可以改变再入过程中横向移动范围。当需要增大横向机动距离时，中间段宽度沿①方向扩大；反之沿②方向收窄。横向机动距离的改变一定程度上影响再入时间，具体方法见3.3.4节。

3.3.2 再入时间影响因素分析

由于再入过程极为复杂，干扰因素众多，首先对能够影响再入飞行时间的因素进行划分，具体如表1所示。其中，主动因素有攻角剖面的切换速度、最小攻角和视线角走廊的宽度等；被动因素有大气不确定、初始投放不确定和动态特性(气动系数、动导数等)不确定等。

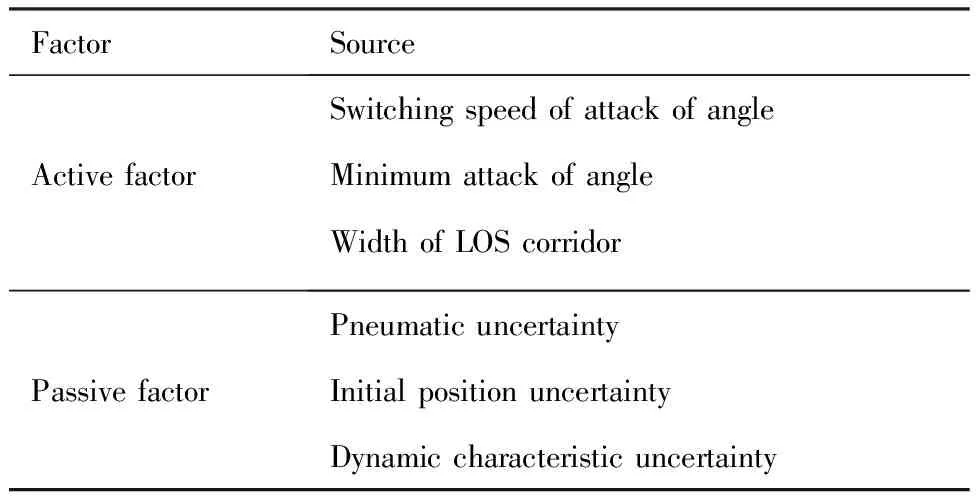
表1 再入时间影响因素Table 1 Influencing factors of reentry time

以标称环境下飞行时间为1 592 s的再入任务为例，对被动因素进行2 000次蒙特卡罗仿真并统计最终飞行时间误差，结果如图 8所示。

图8 被动因素产生的时间误差直方图Fig.8 Histogram of time errors caused by passive factors

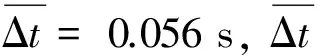
在标称环境下对主动因素进行调节以研究其时间调整能力，结果如表2所示。其中视线角走廊上界的调节是通过设置图7视线角走廊的中间段角度x而实现的。

表2 主动因素的影响Table 2 Influence of active factors

由表2可知，通过对主动因素的调整可以实现再入飞行时间的调节，为再入过程的时间调整提供了可行性的基础。但通过改变攻角剖面进行时间调节的能力有限且能量损耗大。

在传统多弹协同制导律的设计中，通常在基本导引律之上叠加横向过载指令，改变横向机动距离以实现飞行时间的调整[4,7]。高超声速飞行器的操控能力有限，面对称的外形无法直接叠加横向过载，因而最有效地增加横向机动距离的方法是改变视线角走廊的宽度，表2中的视线角走廊宽度与再入飞行时间的关系如图9所示。由图可知，调节视线角走廊宽度可以有效地改变飞行时间且呈单调递增趋势，因而在再入过程中采用动态改变视线角走廊宽度的方法以调整再入飞行时间。

图9 视线角走廊宽度与再入飞行时间Fig.9 Width of LOS corridor vs reentry flight time

3.3.3 协调信息计算

集群内个体之间的信息共享是实现集群协同运行的基础，其中所必需的最小量信息被称之为协调信息或协调变量[6,8]。若每个个体都能接收到相同的协调信息并由此进行动作，则集群的协同运行即可实现。基于协调信息的协同控制作为一种通用方法，为集群协同控制问题提供了一套具有普遍意义的解决方案[6]。

基于协调信息的协同控制方法已成功运用于机器人、无人机等领域之中[7]，因而也为高超声速飞行器时间协同再入制导提供可能的探索方向。由于协同再入飞行的目的是对目标进行饱和打击，该过程要求所有飞行器具有相同的再入飞行时间，因而可将其期望值tneed作为协调信息。

若各飞行器再入飞行时间可知且能够与tneed达成一致，则在多飞行器必然能够同时完成再入飞行过程。期望再入飞行时间tneed的求取是基于对象特点所设计的协调函数[8]。本文的协调函数具有特殊性，主要由于高超声速飞行器控制方式单一且控制过程不可逆。前期仿真表明，调整范围为整个再入时间的4%～5%。以至少需要1 600 s的再入过程为例，可调节的范围在1 600-1 670 s。其次由于再入过程的复杂性，难以实现文献[7]中具有明确物理意义且具有次优性的协调信息。因而需要根据不同的飞行阶段特点设计相应的协调函数以得到协调信息tneed。

在初始下滑段，飞行器气动力和机动能力弱，仅需要将运动方向对准目标和保证存在可行的协同再入时间域即可。因而只在初始投放时刻对各飞行器的可行再入飞行时间范围进行预估并做可协同性分析，即保证多个可行时间域存在重叠，进而求解如式(29)所示的初始可行协调时间:

(29)

式中：tmin,i和tmax,i分别为第i个飞行器的最小和最大飞行时间。在整个初始下滑段中以固定的时间协调信息进行再入轨迹规划。

在所有飞行器进入平衡滑翔段后，气动力和机动能力增强，加之长距离的飞行过程使得其有一定的时间调整能力，此时计算中心根据各飞行器预估时间求解时间协调信息，即

(30)

在第m个制导周期，所有飞行器进入再入终段，此时以减小落点误差和细调再入时间为目标，协调信息沿用第m-1个周期的计算结果:

(31)

3.3.4 时间预估与校正

飞行器再入时间的可知性与可控性是协同制导的基础，在选定视线角走廊宽度作为时间调整变量和定义协调函数之后，构造如图10所示的时间可控再入制导系统。

其中时间预估模块根据当前时刻飞行器状态对剩余再入飞行时间进行预估，实现再入时间的可知性。进而与期望飞行时间(即协调信息)比较得到时间误差为

Δtco=tpre-tneed

(32)

式中：tpre为预估剩余飞行时间。偏差量Δtco通过在线的视线角走廊宽度调整得以消除，实现再入飞行时间的可控性。

再入过程是一个复杂的飞行运动学问题，再入时间与诸多因素有关，现阶段缺乏有效的方法对其进行分析。通过仿真，在固定视线角走廊下，某次再入过程中的不同参数与再入时间关系如图11所示。

图10 时间可控再入制导系统Fig.10 Time-controlled reentry guidance system

在加入视线角走廊宽度之后，图11将更为复杂，本文不再具体展开。基于数值计算的方法很难对如此复杂且连续的函数进行有效的拟合，而神经网络具有较强的自学习、自适应与非线性映射能力，常被运用于关系复杂的非确定问题研究，因此本文将其用于再入过程中的时间预估。前期仿真与理论分析可知再入时间与飞行器当前的高度、速度、剩余距离、视线角、视线角走廊上界有关，即

(33)

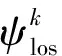
时间预估模块采用如图12所示的BP(Back Propagation)神经网络。在一定大小的训练数据集(105～106及以上)基础上，根据Kosmogorov定理，在合理的结构和恰当的权值条件下，3层BP网络可以逼近任意的连续函数[22-23]。

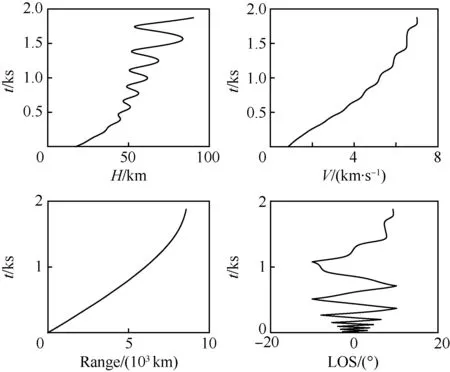
图11 不同参数与再入时间的关系Fig.11 Relationship between different parameters and reentry time

图12 3层BP神经网络Fig.12 Three-layer BP neural network

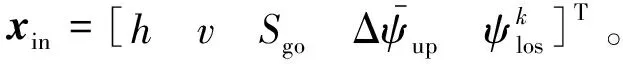
(34)

(35)

输出层采用斜率为ko(ko>0)的ReLU函数：

G(x)=max(0,kox)

(36)

最终输出剩余飞行时间预估值为

(37)

1) 标称环境下，在可达飞行距离范围内等距离选择50个经纬度坐标作为仿真的初始投放点，再入任务目标见表 4。

2) 针对每一个再入过程，横向制导模块的视线角走廊宽度x以1°为步长由3°变化至28°，重复进行再入轨迹仿真，制导仿真周期为1 s。

3) 记录整个仿真过程中的5个飞行器状态量，并由最终的飞行时间倒推出不同状态量所对应的剩余飞行时间，两两结合组成训练集。

通过以上流程可获得大小在2×106级别的时间预估网络训练集。网络训练采用贝叶斯正则化算法以提高其泛化能力和抑制过拟合现象[22]。在每一代的训练过程中，随机选择整个数据集中的85%作训练集，10%作验证集，5%作测试集。隐藏层神经元个数的确定采用网格搜索法，在1000代的训练代数下，网络效果如图13，横坐标nh为隐藏层神经元个数，纵坐标为训练集和测试集的均方根误差(Root Mean Square Error，RMSE)

由图13可知，即使是采用非线性的Sigmoid函数作隐藏层的激活函数，时间预估网络仍然存在一定误差，并且与隐藏层神经元个数存在一定的关系。当神经元个数较少时，网络出现欠拟合；随着数量的增加，网络拟合精度逐渐提高，但在超过一定阈值后出现过拟合现象。在多次测试和综合考虑精度、计算量的基础上，最终选定的网络结构为5-20-1。进而对预估模块实际运行效果进行测试，结果如图14所示。由图可知即使在加入参数拉偏后，整个再入过程中的时间预估误差仍在±7 s以内。其中由于在初始下滑段和再入终段，视线角走廊存在拐点，从而造成较大的估计误差，但不影响总体的时间预估效果。

横向走廊的宽度直接影响了再入过程的横向机动范围，调节横向机动范围可以对再入飞行时间进行调整，并且存在如图9的连续单调递增关系。以图7为例，具体的走廊调整策略如下：

1) 初始下滑段气动能力较弱，需要飞行器对准目标方向，不进行走廊的调整。

图13 隐藏层神经元个数-均方根误差Fig.13 Number of hidden layer neurons vs RMSE

图14 剩余飞行时间预估效果Fig.14 Test results of estimated time-to-go

2) 再入终段为了到达目标点需要一定的视线角限制，不对最终角度进行调整。

3) 调整区域为中间段宽度x，由式(32)得到时间误差Δtco,Δtco<0时，说明以当前视线角走廊飞行，最终再入时间将小于期望飞行时间，需要沿①方向扩大走廊以延长再入时间；同理当Δtco>0时，沿②方向缩小视线角走廊以缩短再入飞行时间。

(38)

(39)

(40)

(41)

(42)

4 仿真验证

针对设计的时间可控再入制导律和协同结构，首先进行标称环境下多任务仿真，验证时间可控再入制导律的自主性与时间可控性；进而进行蒙特卡罗仿真，验证时间可控再入制导律在参数拉偏情况下的鲁棒性；最后进行协同再入仿真，验证整套协同结构的有效性。

由于飞行器控制能力有限，需要对时间调节范围进行限制。本文可行时间调节范围为初始预估飞行时间的0%～4%。不确定性参数采用正态分布，具体如表3所示；再入任务如表4所示。

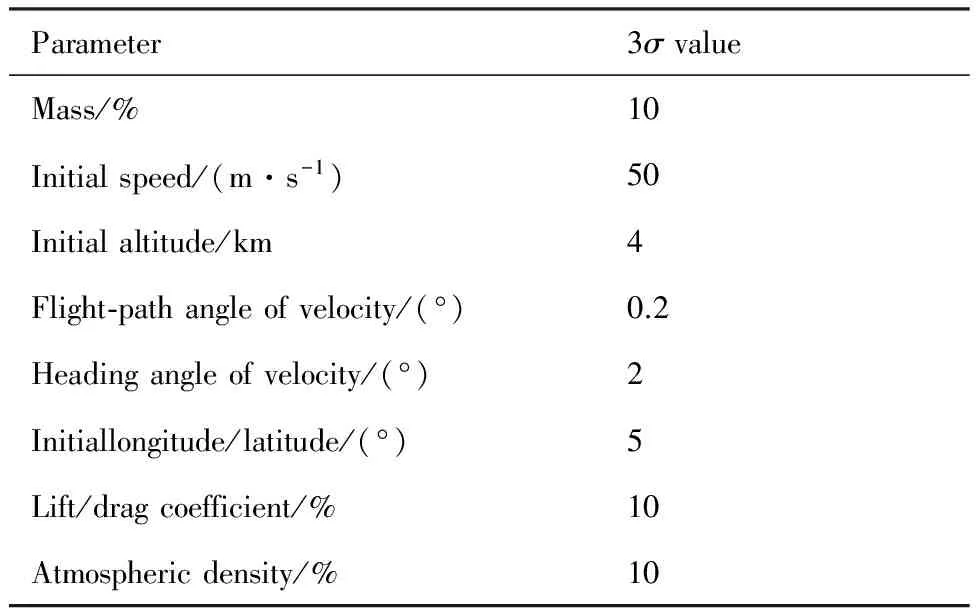
表3 拉偏参数表Table 3 Parameter deviation

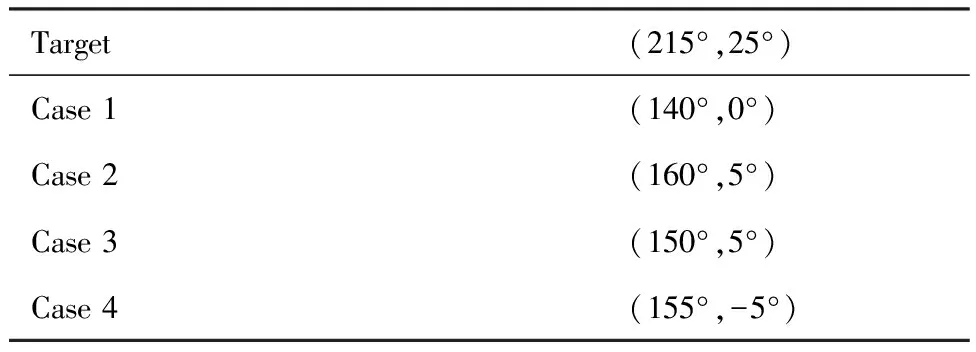
表4 再入任务Table 4 Cases of reentry mission

4.1 多任务仿真

在标称环境下进行多任务指定再入时间仿真，测试时间可控再入制导律的自主性，飞行轨迹如图15所示。以Case 2为例，再入过程中的具体参数如图16～图18。飞行时间误差、制导精度与制导周期平均耗时的对比如表5所示，其中以文献[11]为代表的再入制导律记为“制导律1”(Law 1)，本文的再入制导律记为“制导律2”(Law 2)，二者均在相同软硬件条件下仿真。由图15(b)的轨迹可知，文献[20]中的初始投放条件较为保守，对于飞行过程约束留有较大余量，为进一步测试本文制导律的约束管理能力，加入表3的参数拉偏并将Case 2的初始投放条件改为150 km、6 500 m/s，约束校正效果如图19所示，其中终端约束为16 km、850 m/s。

图15 横向和纵向轨迹Fig.15 Horizonfal and longitudinal trajectory

图16 视线角与走廊变化曲线Fig.16 Changing curves of LOS and corridor

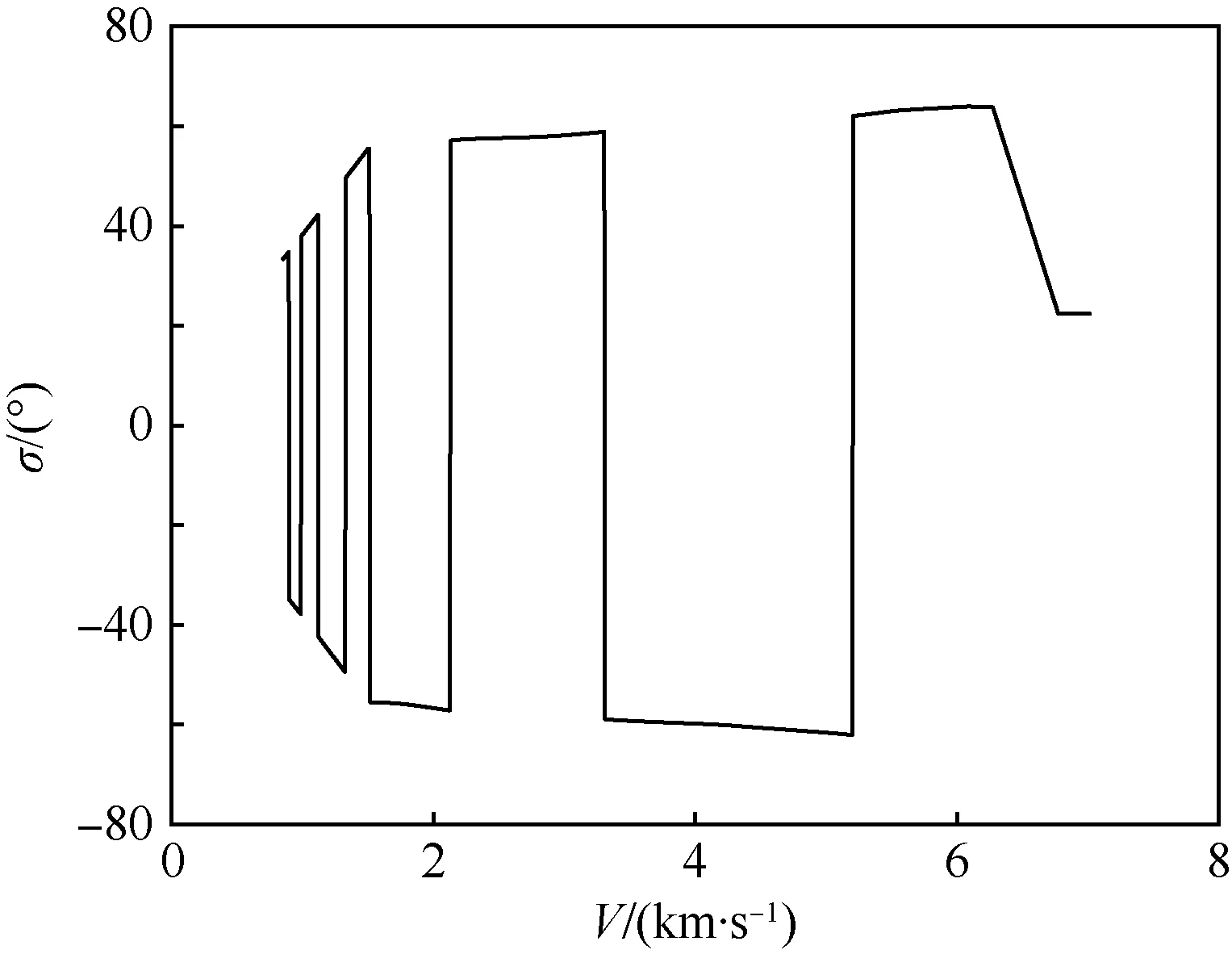
图17 速度-倾侧角剖面Fig.17 Velocity-bank angle profile

图18 剩余飞行时间估计效果(Case 2)Fig.18 Test resuts of estimated of time-to-go (Case 2)

图19 有无在线约束效果对比Fig.19 Comparison of results with and without online constraint management

表5 多任务仿真结果Table 5 Results of multitasking simulation

在初始下滑段，由于飞行器气动能力弱，采取大攻角、固定倾侧角、固定视线角走廊的方式进行再入飞行，因而产生了图 18中的预估时间误差；在进入平衡滑翔段之后，各校正模块工作，预估时间误差快速收敛并稳定趋向于零。与此同时，由于真实走廊存在如图 7所示的线性连接区域，而时间校正模块直接输出的是视线角走廊中间段的宽度x，因而会产生如图 16所示的在初始下滑段和再入终段期望视线角走廊与实际不符的情况。图 16中的再入横侧向走廊在再入时间预估-校正模块的作用下呈现不规则的外形，其正是对时间误差进行主动调节的有效证明。图 17表明倾侧角翻转次数在可接受的范围之内。表 5说明时间可控再入制导律在多任务下均有良好的时间控制能力与较高的制导精度，并且本文预测-校正方法的制导周期平均耗时相对于传统方法缩短了80%以上；图 18说明在线约束强化管理模块的加入，有效地改善了飞行过程中约束违反现象的发生，并且对于终端状态约束的满足提供了更好保障。

4.2 蒙特卡罗仿真

本节以Case 2为对象，记无时间预估-校正模块的制导律为“制导律 3”(Law 3)，时间可控再入制导律为“制导律 4”(Law 4)。在可行时间范围内(1 355～1 408 s)随机选择4个期望时间进行蒙特卡罗仿真，以验证时间可控再入制导律的鲁棒性。拉偏参数见表3，两种制导律在每个期望飞行时间下的仿真次数均为1 000次，最终飞行时间和距离误差的对比如表6所示。以1 390 s为例，时间可控再入制导律轨迹与时间误差如图20～图22所示。

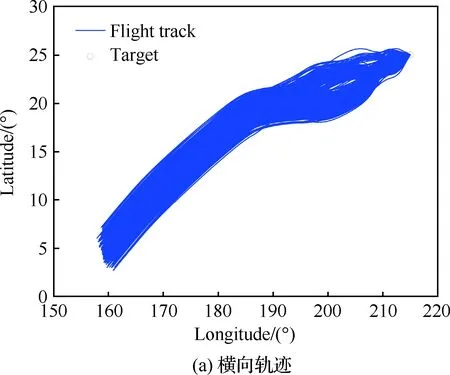
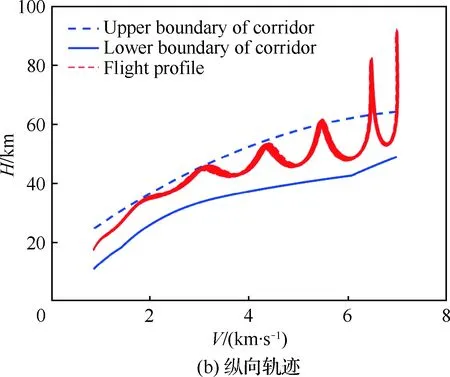
图20 横向和纵向轨迹(Case 2)Fig.20 Horizontal and longitudinal trajectory (Case 2)

表6 蒙特卡罗仿真结果Table 6 Monte Carlo simulation results

图22说明再入飞行时间误差在±10 s以内，满足协同任务需求[3-4]；通过表6的对比可知，时间可控再入制导律可以有效地降低飞行时间误差，并且不会影响制导精度。由仿真可知，时间可控再入制导律在参数不确定性下仍有良好的表现，具有一定的鲁棒性。其主要原因有：

1) 虽然时间预估网络来源于离线训练，但其本身具有一定的泛化能力[22]和较高的精度。

2) 时间预估网络的输入来源于实际飞行状态，而参数不确定性所带来的干扰直接影响当前飞行状态，使其偏离期望值，进而间接地影响预估时间结果，从而产生时间误差。

3) 长距离的飞行过程、轨迹预测校正和时间校正模块的在线迭代使得误差能及时得到修正。

图21 剩余飞行时间估计效果(Case 2)Fig.21 Estimated time-to-go (Case 2)

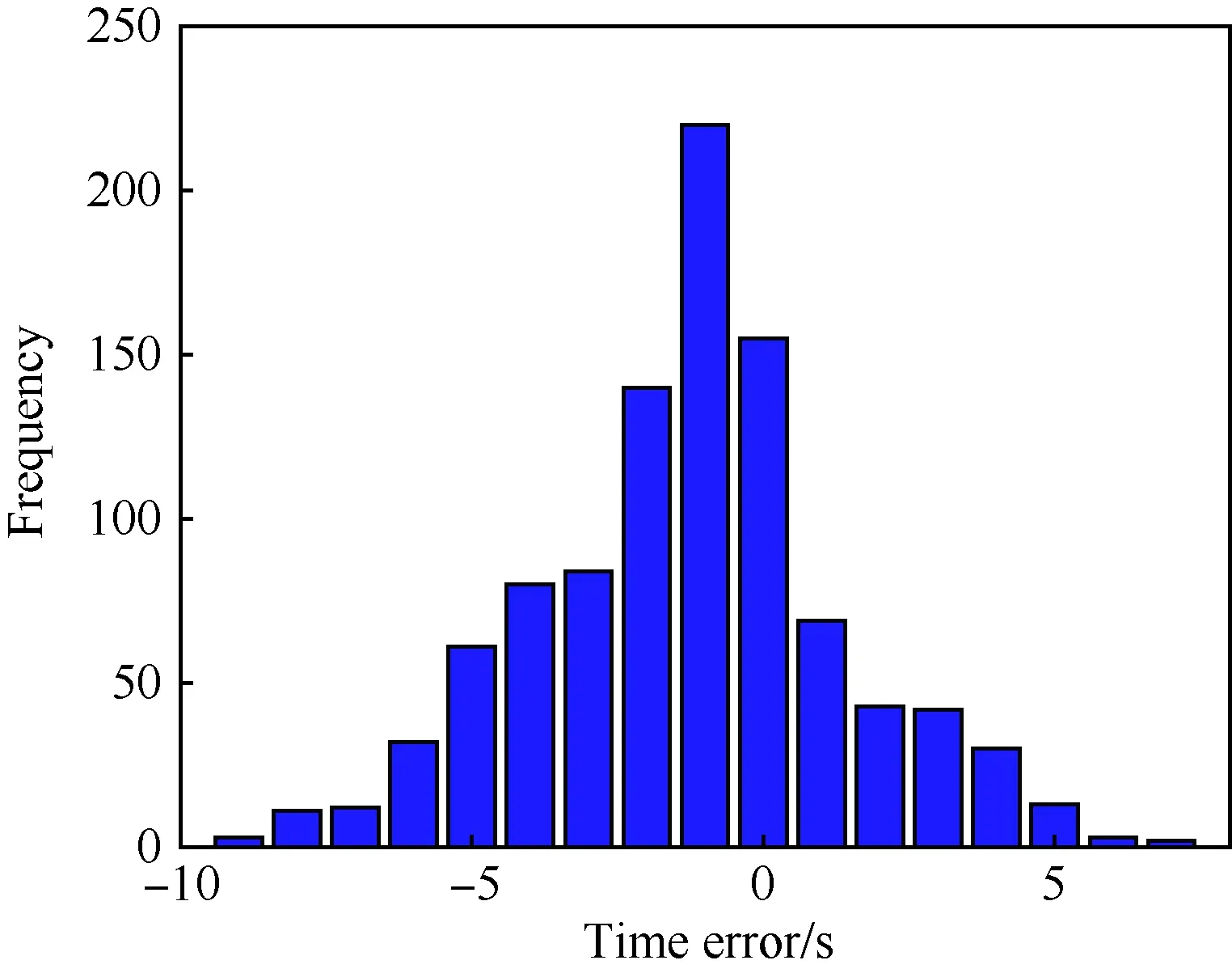
图22 最终飞行时间误差直方图Fig.22 Histogram of final flight time error

4.3 协同再入仿真

针对多高超声速飞行器协同再入任务需求，在协调时间存在的前提下，随机选择5个初始投放点，进行协同再入仿真以验证协同结构的有效性。参数拉偏如表3所示，各飞行器之间相互独立。最终期望协同再入时间为1 702.8 s。最终再入轨迹与协调时间变化曲线如图23和图24所示，协同再入结果如表7所示。

仿真结果表明在整个飞行过程中，期望协同飞行时间信息相对平滑，各飞行器的实际飞行时间均能趋向于期望值。其中在平衡滑翔段，由于参数不确定性等原因的干扰，使得部分飞行器预估时间出现较大误差，但通过时间校正模块和协同结构的共同作用可以有效地将其进行消除。整个飞行过程表明协同结构可以有效的对可协同的多个飞行器进行协调时间计算，而时间可控再入制导律可以有效地将时间协调信息作为约束之一进行实时的在线轨迹预测与校正，实现多飞行器协同再入任务需求。

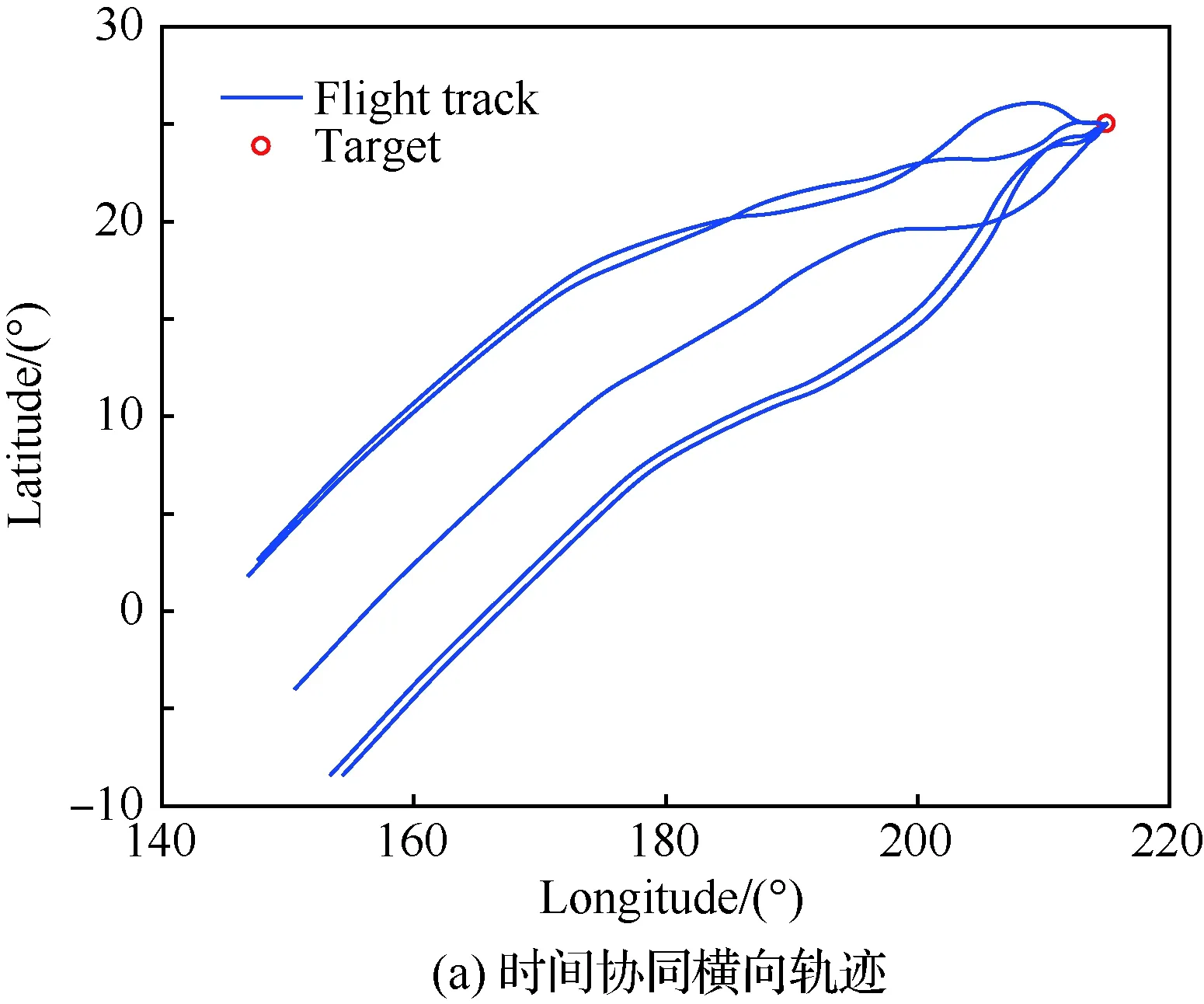
图23 时间协同横向和纵向轨迹Fig.23 Time-coordinated horizontal and longitudinal trajectory

图24 剩余飞行时间估计效果(时间协同)Fig.24 Estimation of time-to-go (time-coordinated)

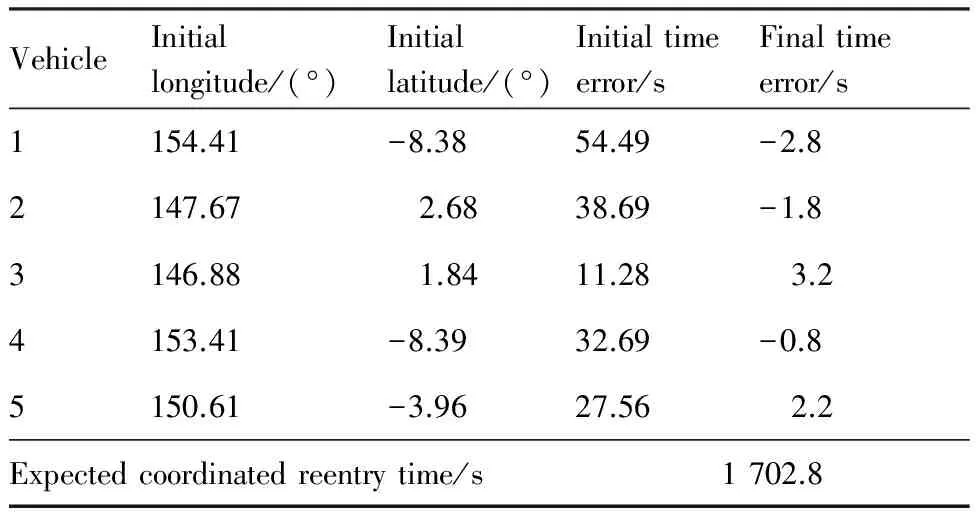
表7 协同再入结果Table 7 Results of collaborative reentry flight

5 结 论

1) 本文针对多高超声速飞行器时间协同再入制导问题，提出协同再入制导架构和时间可控再入制导律。

2) 时间可控再入制导律在跨周期轨迹预测-校正制导律的基础上，通过对时间影响因素的仿真与分析，将横向制导模块中的视线角走廊宽度作为控制量，利用神经网络和Gauss-Newton迭代法实现再入飞行时间的预估与校正。

3) 时间可控再入制导律根据当前实时的飞行状态进行时间预估，得到时间误差并由此对视线角走廊进行动态调整，仿真验证了其具有良好的自主性、鲁棒性、实时性和时间可控性。

4) 协同再入制导架构分为两层，适用于集中式或分布式的通讯结构。上层协调层的协同函数可以根据飞行任务需求进行有针对性设计；下层执行层由时间可控再入制导律进行在线轨迹规划。仿真验证了该结构的有效性，能够实现多高超声速飞行器的协同再入飞行任务需求。

参 考 文 献

[1] 胡冬冬, 刘晓明, 张绍芳, 等. 2016年国外高超声速飞行器技术发展综述[J]. 战术导弹技术, 2017(1): 28-33.

HU D D, LIU X M, ZHANG S F, et al. Review of hypersonic technologies progress abroad in 2016[J]. Tactical Missile Technology, 2017(1): 28-33 (in Chinese).

[2] 高雁翎, 张梦湉, 贾晨阳. 2016年国外防空反导发展综述[J]. 战术导弹技术, 2017(2): 16-20.

GAO Y L, ZHANG M T, JIA C Y. Development review of world air and missile defense system in 2016[J]. Tactical Missile Technology, 2017(2): 16-20 (in Chinese).

[3] 李聪颖, 韩蕾, 高晓冬, 等. 再入反舰导弹多弹协同饱和攻击突防最优弹道研究[J]. 指挥与控制学报, 2015, 1(1): 72-80.

LI C Y, HAN L, GAO X D, et al. Study on optimalpe-netration trajectories of multi reentry anti-ship missiles for cooperative saturation attack[J]. Journal of comma-nd and control, 2015, 1(1): 72-80 (in Chinese).

[4] 王少平, 董受全, 李晓阳, 等. 助推滑翔高超声速反舰导弹多方向协同突防可行性研究[J]. 指挥控制与仿真, 2017, 39(2): 55-60.

WANG S P, DONG S Q, LI X Y, et al. Feasibility study of multi-direction coordinated penetration of the boost-glide hypersonic anti-ship missile[J]. Command Control and Simulation, 2017, 39(2): 55-60 (in Chinese).

[5] JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266.

[6] 赵世钰, 周锐. 基于协调变量的多导弹协同制导[J]. 航空学报, 2008, 29(6):1605-1611.

ZHAO S Y, ZHOU R. Multi-missile cooperativeguid-ance using coordination variables[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1605-1611 (in Chinese).

[7] ZHAO S Y, ZHOU R. Cooperativeguidance for multi-missile salvo attack[J]. Chinese Journal of Aeronautics, 2008, 21(6): 533-539.

[8] MCLAIN T W, BEARD R W. Coordinationvariables, coordination functions, and cooperative timing mission[J]. Journal of Guidance Control & Dynamics, 2005, 28(1): 150-161.

[9] 张友安, 马国欣, 王兴平. 多导弹时间协同制导: 一种领弹-被领弹策略[J]. 航空学报, 2009, 30(6): 1109-1118.

ZHANG Y A, MA G X, WANG X P. Time-cooperative guidance for multi-missiles: A Leader-Follower strategy[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1109-1118 (in Chinese).

[10] 赵启伦, 陈建, 李清东, 等. 高超武器与常规导弹协同攻击策略可行域研究[J]. 航空学报, 2015, 36(7): 2291-2300.

ZHAO Q L, CHEN J, LI Q D, et al. Feasible region of hypersonic and ballistic missiles’ cooperative attack strategy[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2291-2300 (in Chinese).

[11] LU P. Entry guidance: A unifiedmethod[J]. Journal of Guidance Control & Dynamics, 2014, 37(3): 713-728.

[12] 刘思源, 梁子璇, 任章, 等. 高超声速滑翔飞行器再入段制导方法综述[J]. 中国空间科学技术, 2016, 36(6): 1-13.

LIU S Y, LIANG Z X, REN Z, et al. Review of reentry guidance methods for hypersonic gliding vehicles[J]. Chinese Space Science and Technology, 2016, 36(6): 1-13 (in Chinese).

[13] WANG Z, GRANT M J. Constrained trajectory optimiza-tion for planetary entry via Sequential convex program-ming[C]∥AIAA Atmospheric Flight Mechanics Conference. Reston, VA: AIAA, 2017: 1-13.

[14] CHENG L, WANG Z, CHENG Y, et al.Multiconstrain-ed predictor-corrector reentry guidance for hypersonic vehicles[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2017: 095441001772418.

[15] KURIKI Y, NAMERIKAWA T. Consensus-based coop-erative formation control with collision avoidance for a multi-UAV system[C]∥American Control Conference. Piscataway, NJ: IEEE Press, 2014: 2077-2082.

[16] BRARD R W, MCLAIN T W, GOODRICH M A, et al. Coordinated target assignment and intercept for unmanned air vehicles[J]. IEEE Transactions on Robotics & Automation, 2002, 18(6): 911-922.

[17] TOMIC S, BEKO M, RUI D. RSS-Based localization in wireless sensor networks using convex relaxation: noncooperative and cooperative schemes[J]. IEEE Transactions on Vehicular Technology, 2015, 64(5): 2037-2050.

[18] SHI P, SHEN Q. Cooperative control of multi-agent systems with unknown state-dependent controlling effects[J]. IEEE Transactions on Automation Science & Engineering, 2015, 12(3): 827-834.

[19] 林涛, 刘永才, 关成启, 等. 飞航导弹协同作战使用方法探讨[J]. 战术导弹技术, 2005(2): 8-12.

LIN T, LIU Y C, GUAN C Q, et al. An investigation into the methods of cooperative engagenment for aerodynamic missile[J]. Tactical Missile Technology, 2005(2): 8-12 (in Chinese).

[20] 王光伦. 高超声速飞行器再入段预测校正制导研究[D]. 哈尔滨: 哈尔滨工业大学, 2010: 18-19.

WANG G L. Predictor-corrector reentry guidance for hypersonic vehicles[D].Harbin: Harbin Institute of Technology, 2010: 18-19 (in Chinese).

[21] PHILLIPS T H. A common aero vehicle (CAV) model, description, and employment guide[R]. Albuqerque, New Mexico: Schafer Corp-oration for AFRL and AFSPC, 2003.

[22] SUTTON R, BARTO A. Reinforcement Learning: An Introduction[M]. Massachusetts: MIT Press, 2005: 235-304.

[23] DU X, GAO M F.The application of identifying numbers on artificial neural network[J]. Computer Systems Applications, 2007(2): 21-22.