飞机主馈线单相交流电阻解析计算方法

张瑶佳，王莉,*，王晓慧，刘伟，阮立刚

1.南京航空航天大学 自动化学院，南京 211100 2. 上海飞机设计研究院，上海 201210

主馈线是指从飞机主发电机的输出端至发电机汇流条之间的导线，其性能与电源系统的重量、电能质量和可靠性密切相关。主馈线是飞机交流电源系统的重要环节，发电系统调压点的电压等于发电机端电压与主馈线的压降之差，发电机除了要为负载提供功率，还需要提供主馈线消耗的有功和无功功率，主馈线上阻抗的存在增加了发电机的负担；另外，主馈线阻抗对电能质量也有明显的影响，这种影响在大容量负载起动或切换过程、发电机或者配电线路故障等瞬态过程中更加严重，易导致电压瞬变超出标准中规定的瞬态范围极限，从而危害到负载设备[1-2]。所以，开展飞机主馈线的阻抗研究具有重要的意义。

目前大型飞机正朝着全电化和多电化的方向发展[3-4]，电源系统的容量也越来越大。变频交流电源系统具有结构简单、可靠性高、效率高、费用低的优点，因而适合作为大容量的飞机交流电源系统，是大型飞机的发展趋势之一[5]。大型飞机变频交流电源系统的显著特点是容量大大提高，且主馈线的长度显著增加。其稳态电源频率范围是360～800 Hz，最高频率相比传统400 Hz恒频交流电源系统提高了一倍。频率的提高以及主馈线长度的增加引起主馈线阻抗增大，并且由于电源系统容量的提高，主馈线电流大大增加，因此主馈线电压损失和损耗的问题非常突出。在变频系统中，较高频率时电压不平衡度会更大，这主要是由于馈线阻抗的增大所引起的，并且主馈线阻抗将对系统带不平衡负载能力、开关过程的瞬态电压、电压跌落及波形畸变等产生较大影响；因此，为了提高电源系统电能质量，也必须开展主馈线阻抗的优化方法研究。

在变频交流电源系统中，主发电机的频率范围为360～800 Hz，在实际运行过程中有谐波输出，其谐波电流频率考虑在20 kHz以内，集肤效应和邻近效应对主馈线阻抗值的影响不能忽略[6-7]。由于交流电阻是计算压降和损耗的主要参量，所以在考虑谐波频率后的宽频带范围内，对主馈线交流电阻值的计算显得至关重要。考虑到谐波的影响，需要计算0～20 kHz频率范围内的交流电阻值，如果依旧使用传统有限元仿真软件ANSOFT的涡流场模块求解集肤效应和邻近效应对电阻值的影响[8-9]，需要进行大量的重复工作，过程繁琐，所以研究解析计算方法计算宽频率范围内的交流电阻值有着重要意义。

1915年，Kennelly等采用实验方法分析了不同形状导体受集肤效应和邻近效应的不同影响，并且进一步验证了基于贝塞尔函数的集肤因子计算方法的正确性[10]。2013年，加拿大多伦多大学电气工程系的Patel等给出了一种将导纳算子和矩量法相结合的数值计算方法，该方法能够计算圆导体计及集肤效应和邻近效应的交流阻抗值，但仍是基于贝塞尔函数，公式复杂，不利于工程计算和进一步推广[11]。2014年，英国电气工程师Payne从等效导电面积的角度求取了单根导体交流电阻值，同时给出两根导体间邻近因子的计算方法，较传统基于贝塞尔函数的方法更加简单，易于推广，但是该计算方法的适用范围有一定的局限性，在导体间通有反相电流时交流电阻的计算误差很大，达到16%[12]。

国内针对集肤效应和邻近效应的计算也有一定的研究，文献[13]提出一种准确性与有限元法相当，而计算要简单得多的数值计算方法，通过损耗之比和漏磁场能量之比来计算异步电机双笼转子导条的集肤效应系数；文献[14]基于磁性元件绕组的一维模型，对平面磁性元件绕组中的涡流效应进行分析，采用Dowell计算受集肤效应和邻近效应影响的绕组损耗；文献[15]采用基于正弦时变电磁场的复数模型，推导了有限公式法二维涡流电磁场的计算公式，计算了鼠笼电机转子导条的集肤效应；文献[16]采用双转子支路的等效模型对笼型感应电机转子参数的电阻校正系数和槽漏感校正系数进行计算；文献[17]借助有限元仿真数据，建立空心绕组交流电阻系数的经验公式，将经典Dowell解析计算公式拓展至空心绕组的交流电阻计算中。以上文献在研究集肤效应和邻近效应的解析计算方法中具有一定的指导意义，但是研究对象大多针对电极转子导条，无法对圆形导体适用；另一方面，解析计算方法普遍比较复杂，不利于工程应用。

综上，目前对集肤因子和邻近因子的计算方法主要有以下几种：基于有限元的数值计算方法、基于贝塞尔函数的计算方法、基于经验公式的计算方法以及基于等效导电面积的计算方法。① 基于有限元的数值计算方法需要借助有限元仿真软件，进行大量的重复仿真工作，过程繁琐；② 基于贝塞尔函数的计算方法公式复杂，不利于工程计算和进一步多根导体交流电阻的推广研究；③ 采用经验公式计算交流电阻值的方法，具有物理含义不明确的缺点，修正系数随着导体参数的变化需要重新推导计算，普适性不强；④ 基于等效导电面积计算交流电阻的方法，该方法具有公式简单、物理意义明确的优点，但是当两根导体中心距离很小时，计算误差较大，不适用于两根导体相互靠近的情况。所以，现有的集肤因子和邻近因子计算方法受公式复杂度、物理含义及适用范围的限制很大，并不能快速准确地计算出两根导体在任意条件下的交流电阻值。所以本文对两根导体的交流电阻计算方法进行研究，使其具有通用性，扩大了适用范围，公式简单，易于推广，便于工程计算，具有重要的应用价值。

本文主要以大型飞机变频交流电源系统为应用背景，对两根导体间交流电阻解析计算方法进行优化推导，使其具有通用性，扩大适用范围，即在电流频率、导体本身的尺寸及两根导体间的相对位置改变时，仍然可以保证较高的计算精度。取代耗时长、过程繁琐的有限元仿真的方法，具有重要的工程应用价值。

1 电阻受集肤效应和邻近效应影响原理

本文以大型飞机变频交流电源系统为研究背景，主馈线上所通电流的频率范围为360～800 Hz，谐波电流频率考虑在20 kHz以内，所以在0～20 kHz范围内考虑集肤效应和邻近效应对电缆交流电阻值的影响[18-19]。

1.1 集肤效应原理

当交变电流通过导体时，电流密度在导体横截面上的分布是不均匀的，并随着频率的升高，电流越来越集中于导体的表面附近，导体内部的电流密度越来越小，这被称为集肤效应。

集肤效应会使导体交流电阻增加，这里引入集肤因子αR的概念:

(1)

式中：Risolated为单根导体考虑集肤效应影响的交流电阻值；RDC为单根导体直流电阻值。

集肤因子的计算公式为[12]

(2)

式中：f为电流频率；dw为单根导体直径；δ为集肤深度；μ为磁导率；σ为电导率。

1.2 邻近效应原理

当相邻导体流过交变电流时，由于电磁作用使电流偏向一边的现象称为邻近效应。在主馈线中通过交流电流时，导体内电流会因邻近效应的作用偏向一侧，导体材料、半径、频率对邻近效应的影响规律与集肤效应相似。不同的是，邻近效应还受主馈线敷设方式和相互间敷设距离等因素的影响。

两根导体间由于邻近效应会导致电阻值增加，这里引入电阻邻近因子的概念:

(3)

式中：R为两根导体间同时考虑集肤和邻近效应影响的交流电阻值。

邻近因子的计算受多种因素影响，现有的计算方法大多推导过程繁琐，英国电气工程师Payne所提出的邻近因子计算方法过程相对简单，并且具有一定的物理含义，但是适用范围有限。本文在Payne公式的基础上，解决该计算方法存在的不足，得到两根导体间交流电阻的通用解析计算方法。

Payne给出的邻近因子的计算公式为

(4)

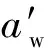
2 两根导体交流电阻计算方法优化

2.1 Payne计算方法存在的问题

由于邻近效应的影响和两根导体的电流方向有密切的关系，所以在邻近因子的计算中，需要分两根导体所通电流同向和反向两种不同情况讨论。

1) 电流反向

当两根导体通有反向电流时，电流密度J分布如图1所示。

根据电轴法，设想将两圆柱导体表面的电荷效应用两根很长的带电细线代替[20]，由于邻近效应的影响，等效带电细线的位置会偏离圆心，如图2所示，A1、B1为实际的等效带电点。

那么，导体A和导体B交流电阻的计算公式为

(5)

图1 电流反向时电流密度分布Fig.1 Current density distribution in opposed current

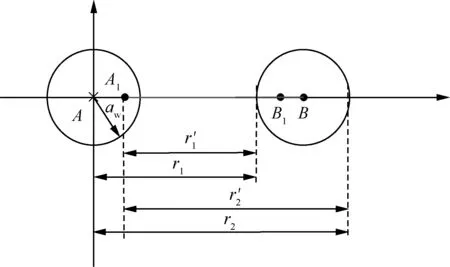
图2 两根导体间等效间距(电流反向)Fig.2 Equivalent spacing between two conductors (opposed current)

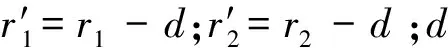
为验证式(5)的正确性，选用线规为AWG 0000#的电缆，结构如图3所示，导电部分的半径r=5.842 mm，含绝缘层的外径Rout=7.82 mm，改变导体A和导体B间的中心距离p，分别取16、20、25、32、50和100 mm。用式(5)计算得到两根导体的交流电阻值和有限元仿真值进行对比，误差曲线如图4所示。

从图4中的结果可以看出，当中心距离较小时，误差较大，两根导体紧密靠近时的误差可达16%，中心距离为20 mm时误差也有6%，当中心距离大于25 mm后，误差较小，计算较精确，此时的最大误差虽在5%左右，但只存在于个别的频率点，多数点误差在2%以内。

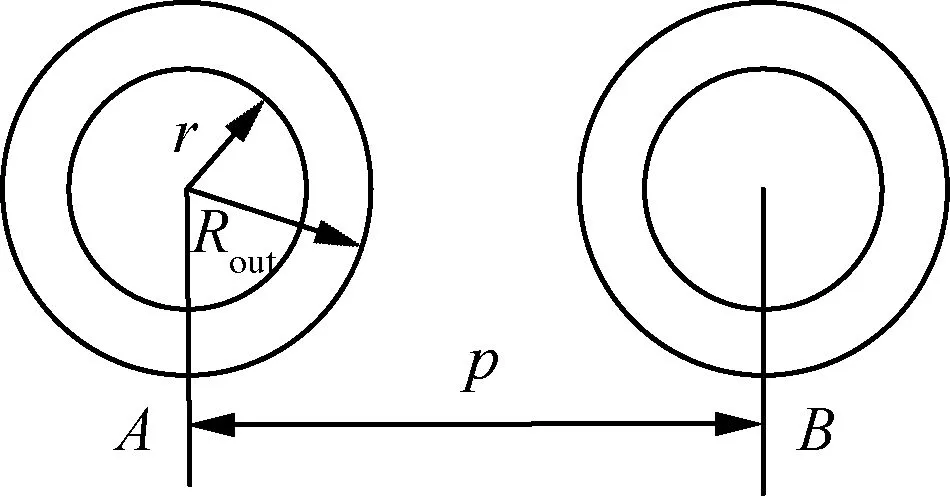
图3 两根导体结构示意图Fig.3 Schematic diagram of structure of two conductors

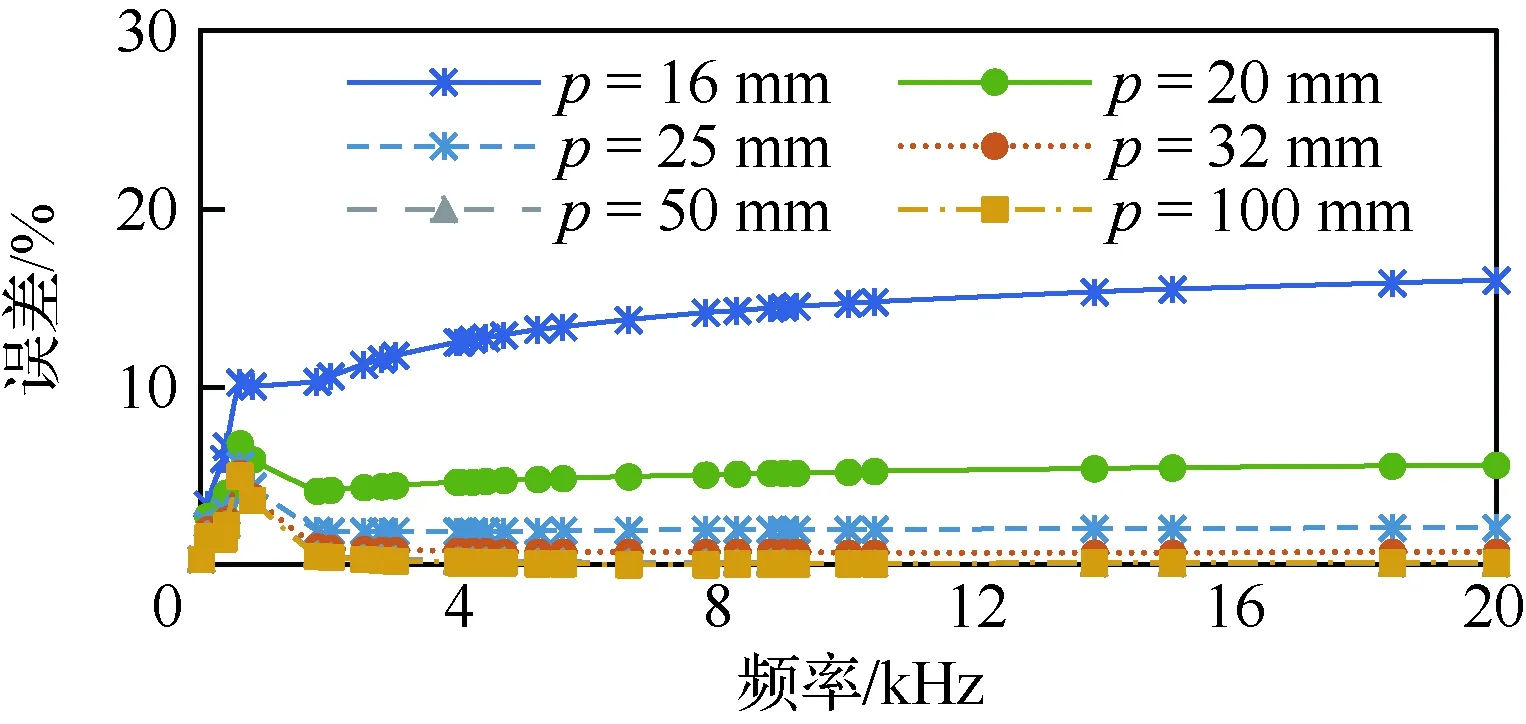
图4 两导体交流电阻计算误差曲线(电流反向)Fig.4 Calculation error curves of AC resistance of two conductors (opposed current)

很明显，当两根导体中心距离较近时，Payne的计算方法并不能准确计算交流电阻值，这是目前无法解决的问题。

2) 电流同向

当两根导体通有同向电流时，电流集中于相互远离的一侧，电流密度分布如图5所示，此时分析和计算方法与电流反向时相同，在此不再赘述。

同样的，对两根导体电流同向时的计算结果进行验证，验证条件和反向时相同，此时的计算值和仿真值误差曲线如图6所示。

电流同向时，在任意中心距离下，交流电阻计算公式的最大误差在5%左右，多数点误差在1%以内，计算结果较精确。

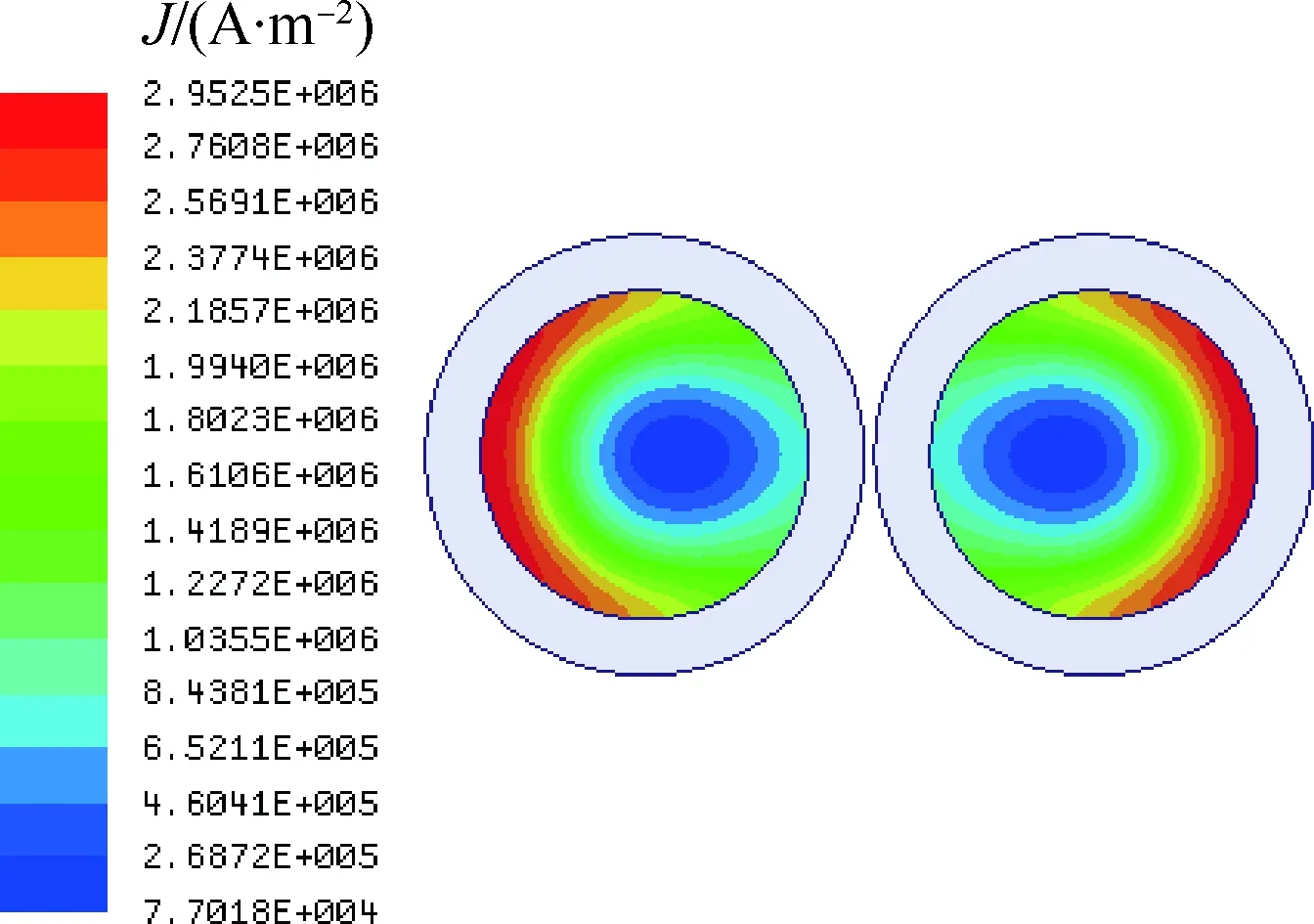
图5 电流同向时电流密度分布Fig.5 Current density distribution in same current

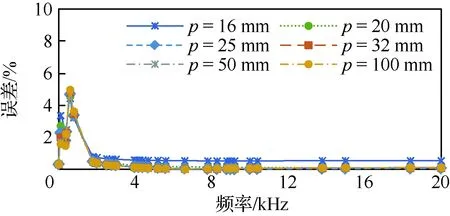
图6 两导体交流电阻计算误差曲线(电流同向)Fig.6 Calculation error curves of AC resistance of two conductors (same current)

2.2 交流电阻解析计算方法优化

2.1节已经提到，当两根导体间所通电流方向相反时，在相互靠近时交流电阻公式计算误差很大，为解决这个问题，从邻近效应的原理出发，对交流电阻计算方法重新进行优化研究。

Payne在推导邻近因子的计算方法中考虑了导体A产生的磁力线和磁场强度对导体B的影响，由于导体B存在于导体A的磁力线范围内，涡流损耗导致了导体A交流电阻值的增长，这就是邻近效应的表现。所以要解决误差大的问题，首先需要研究导体A磁力线的分布情况。

在有限元仿真软件ANSOFT中进行建模分析，仿真条件为：线规AWG 0000#(r=5.842 mm，Rout=7.82 mm)，导体材料为Cu，考虑谐波的频率范围为0～20 kHz，两根导体中所通电流反向，IA=150 A，IB=0 A，中心距离分别取p=16,25,50 mm。仿真得到的磁力线A分布如图7所示(图中左边为导体A，右边为导体B)。

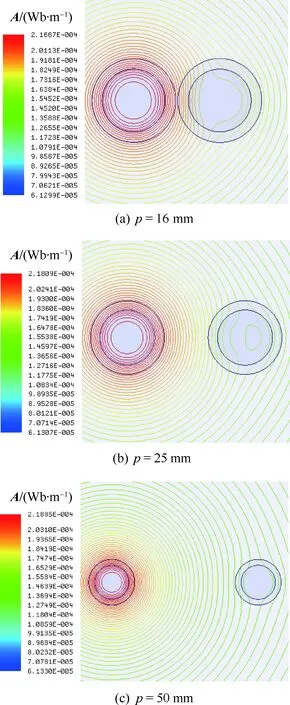
图7 磁力线分布Fig.7 Distribution of magnetic field line

从图7中明显可以看出，导体A产生的磁力线并不是均匀分布的，而是在导体B内部有一个比较严重的畸变，这种畸变随着两根导体中心距离的增大而变小。

对畸变产生的原因进行解释：如图8所示，由于导体A中通有交流电流iA，产生交变的磁场BA，交变的磁场通过导体B中的某一截面时会产生涡流iAB，这就是邻近效应在导体B中产生感应电流，感应电流会在导体B中产生感应磁场，感应磁场与原有磁场相叠加所导致的磁力线畸变，在两根导体距离较近的时候畸变比较严重，随着两根导体中心距离的增加，畸变减小，所以磁力线呈现图7中的规律变化。

ANSOFT软件中的电流密度分布云图很好地印证了上面的解释，如图9所示。

接下来考虑磁力线畸变的影响，重新推导邻近因子解析计算公式，具体过程为：

导体A中有交变的电流流过，会产生交变的磁场，而导体B存在于变化的磁场中，根据电磁感应定律，会产生感应电流，从而引起涡流损耗的发生。涡流损耗的计算公式结合麦克斯韦第一方程可以得到导体在距圆心为r处产生的磁力线的功率损耗[21]：

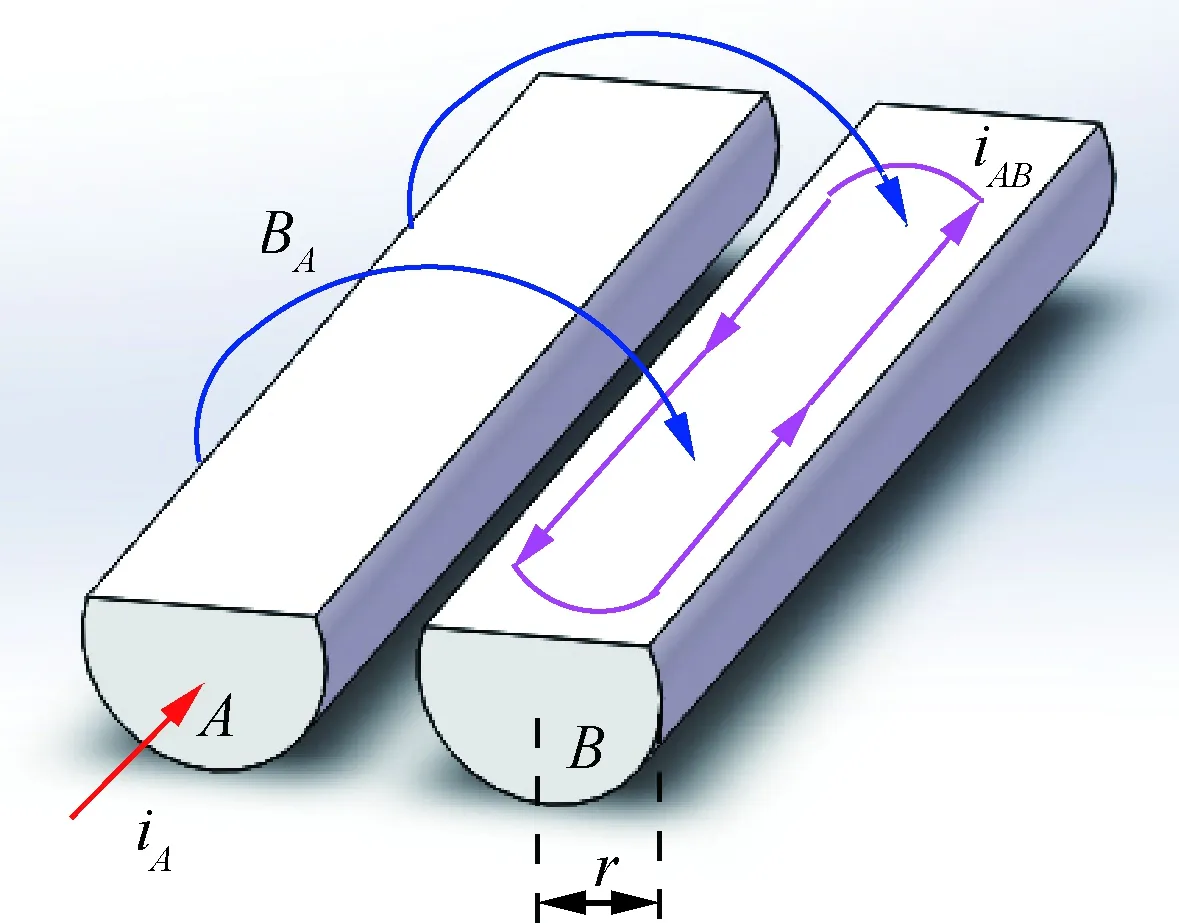
图8 两根导体邻近效应示意图Fig.8 Schematic diagram of proximity effect of two conductors

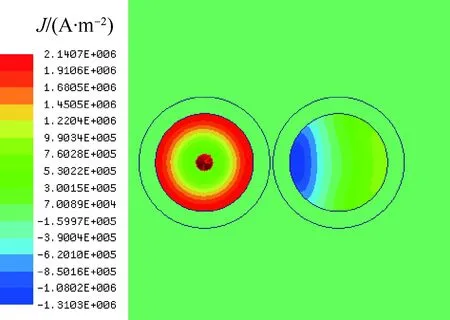
图9 电流密度分布云图(p=16 mm)Fig.9 Distribution of current density contour (p=16 mm)

(6)

式中：K为常数;Rr为由于导体A的涡流损耗在r处增加的交流电阻值。

Pr=I2Rr

(7)

Hr=I/(2πr)

(8)

Rr=K/(2πr)2

(9)

在r处产生的交流电阻Rr与单根交流电阻值R0的比值，即导体A磁力线在r处产生的电阻增量，即

Rr/R0=(aw/r)2

(10)

如图10所示，导体B存在于导体A的磁场中，由于导体B的存在导致了交流电阻的增加，这部分增量是由于导体A的交变磁场在导体B上产生了涡流损耗所致，这里采用磁力线表征导体A对导体B的影响，那么对导体B上所有的磁力线进行积分即可求得由于邻近效应的存在电阻增加的部分。

以AWG 0000#为例，此时中心距离p=16 mm，由于畸变，导体A产生的磁力线在导体B内部磁力线分布如图11所示。

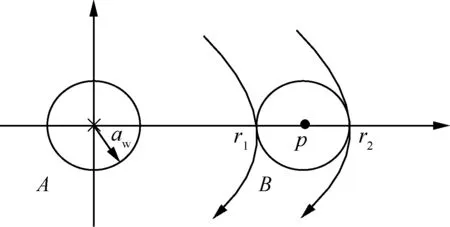
图10 两根导体磁力线分布示意图Fig.10 Schematic diagram of magnetic line distribution of two conductors

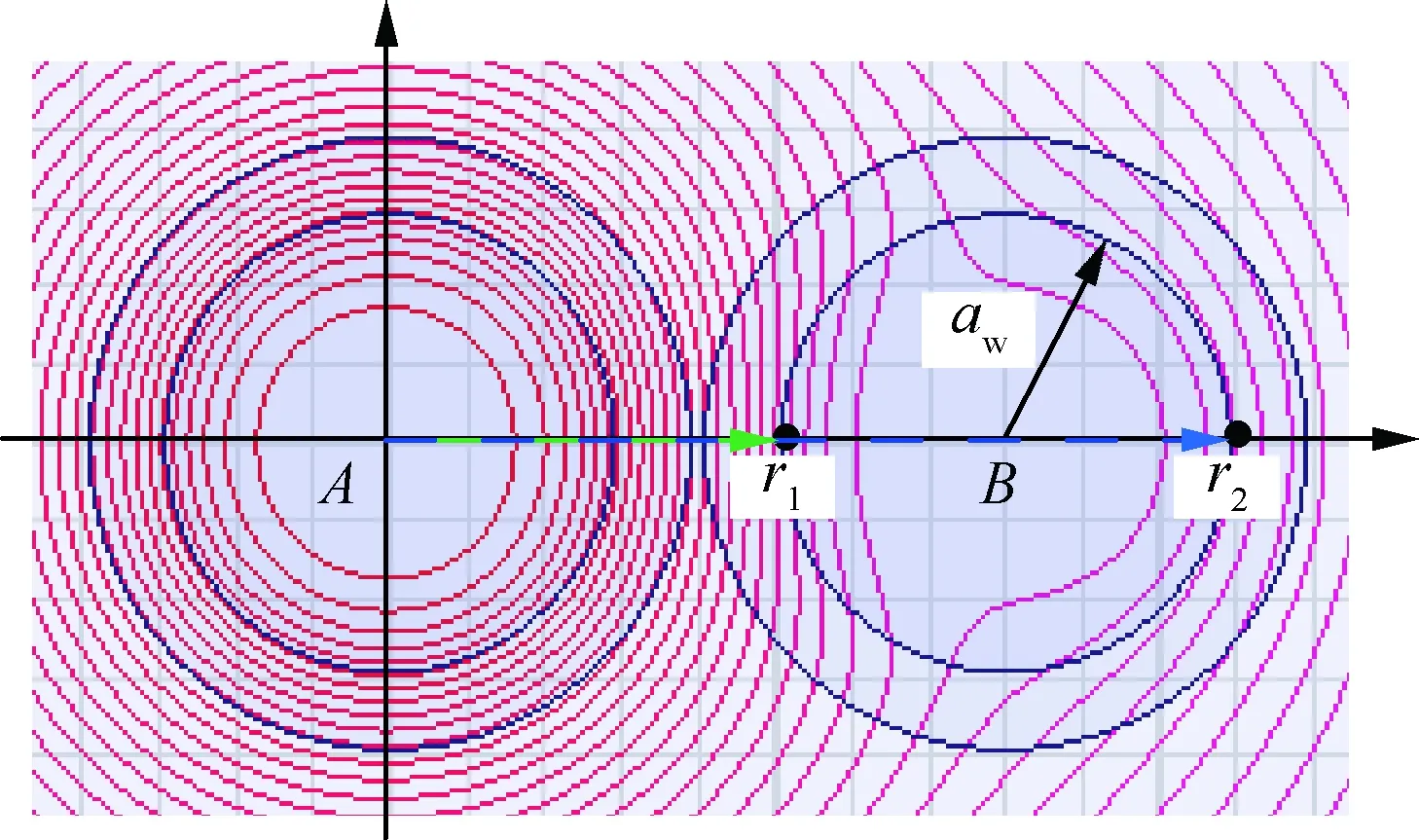
图11 磁力线分布图(p=16 mm)Fig.11 Magnetic line distribution map (p=16 mm)

积分区间为[r1,r1+aw/2]和[r2-aw/2,r2]。

在新的区间范围内进行积分，邻近因子计算公式为

(11)

考虑集肤效应和邻近效应对导体电流密度分布影响后，导体A的总电阻为

(12)

根据对称性，导体B的交流电阻值与导体A相等。

用式(12)对两根导体不同中心距离下的交流电阻进行计算，在单根导体线规为AWG 0000#条件下，误差曲线如图12所示。

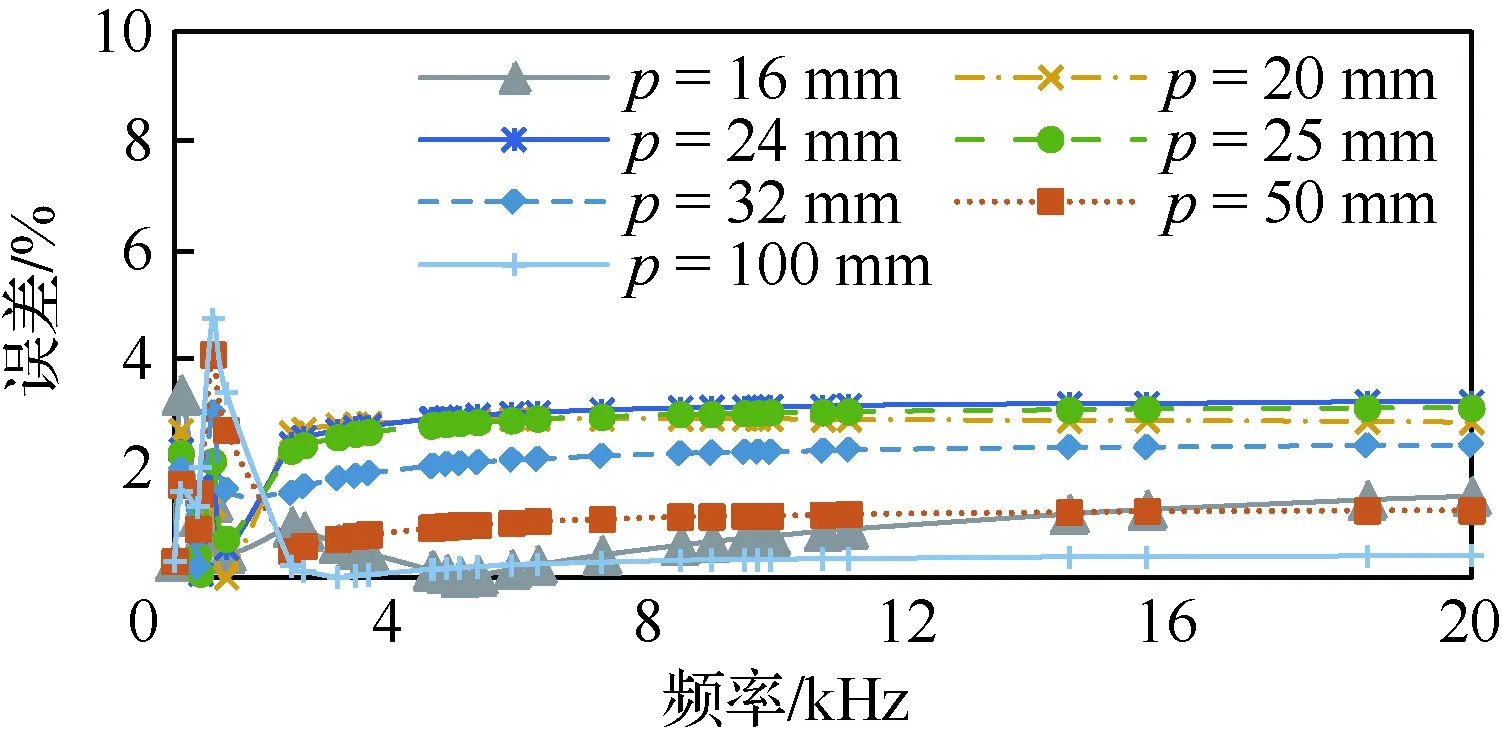
图12 两导体交流电阻计算误差曲线(AWG 0000#)Fig.12 Calculation error curves of AC resistance of two conductors (AWG 0000#)

从图12中可以看出，最大误差在5%左右，多数点误差在2%左右，所以修正后的公式能够很好地计算两根导间的交流电阻值，解决了中心距离较近时误差较大的问题。

2.3 交流电阻解析计算方法仿真验证

为了验证式(12)的普适性，改变导线半径和中心距离进行验证，验证条件为：在AWG 0#线规下，依旧保持两根导体间所通电流反向，求解两根导体不同中心距离下的交流电阻值。导体参数：半径为4.126 mm，中心距离分别取12、15、18、20、25、30、50、100 mm，考虑谐波的频率范围为0～200 kHz，通电电流为150 A，导体材料为Cu。计算得到的误差曲线如图13(a)所示。

在AWG 6#线规下，线径较小，验证此时交流电阻计算公式的准确性。依旧保持两根导体间所通电流反向，求解两根导体不同中心距离下的交流电阻值。导体参数：导体半径为2.057 5 mm，导体外径为2.94 mm，中心距离分别取6、8、9、10、15、50和100 mm，考虑谐波的频率范围为0～20 kHz，通电电流为150 A，导体材料为Cu。

从图13(b)中的仿真验证结果可以看出，在不同的导体半径和中心距离下，优化后的解析计算公式均能将计算误差保证在5%以内，能够准确地计算两根导体的交流电阻值。

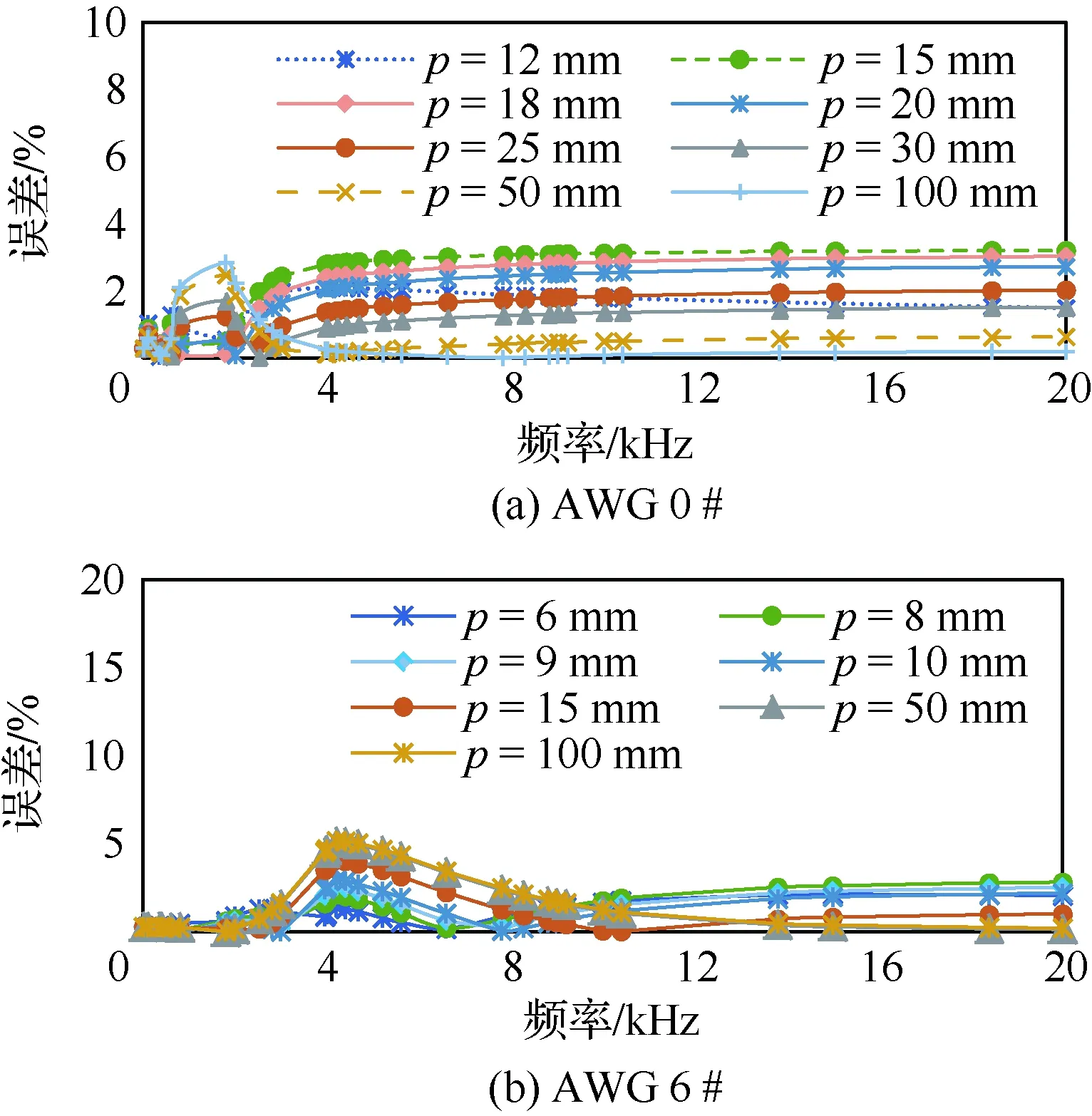
图13 两导体交流电阻计算误差曲线Fig.13 Calculation error curves of AC resistance of two conductors

2.4 交流电阻解析计算方法对比研究

本节对已有的Payne公式和优化后的式(12)进行对比研究，证明本文推导的公式具有明显优势。以AWG 0000#线规、中心距离p=16 mm为例，将优化后的交流电阻计算式(12)的计算结果与Payne公式的计算结果进行对比，如图14所示。从图14中可以看出，优化后的公式基本和仿真值相吻合，更能反映交流电阻值随频率变化的趋势。

为了更好地说明式(12)的优势，将两种公式在不同线规、不同中心距离、不同频率下的计算误差进行对比。所选用的线规分别为：AWG 0000#、AWG 0#、AWG 6#，考虑每种线规紧密靠近的情况，即中心距离分别为16、12、6 mm，频率点在0～20 kHz范围内任取，误差对比结果如表1所示。

很明显，优化后的计算更加准确，将误差从16%降低到了2%左右，新计算方法不再受两根导体间中心距离的制约，适用范围更广。

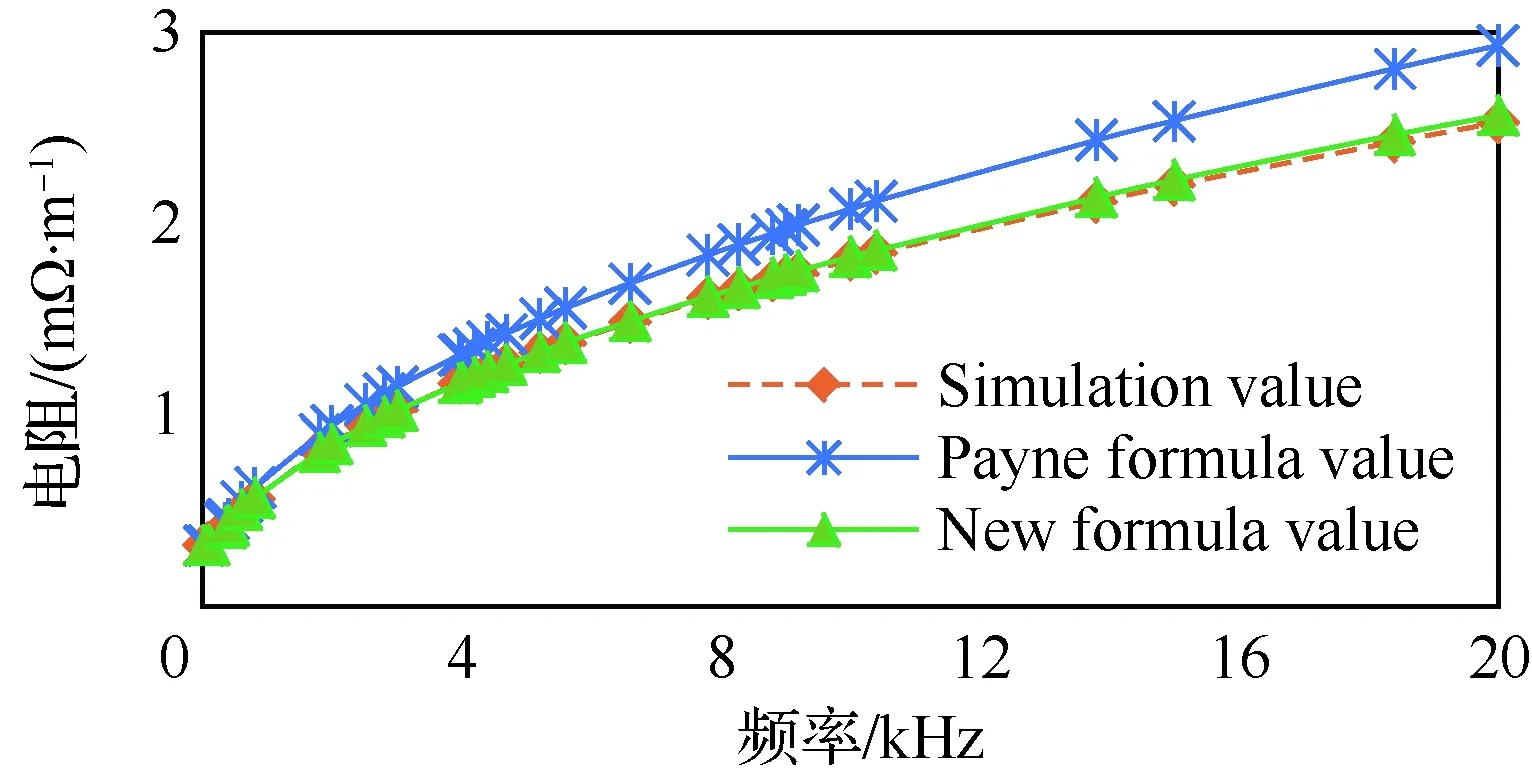
图14 公式优化前后计算值对比Fig.14 Comparison of calculation value before and after formula optimization

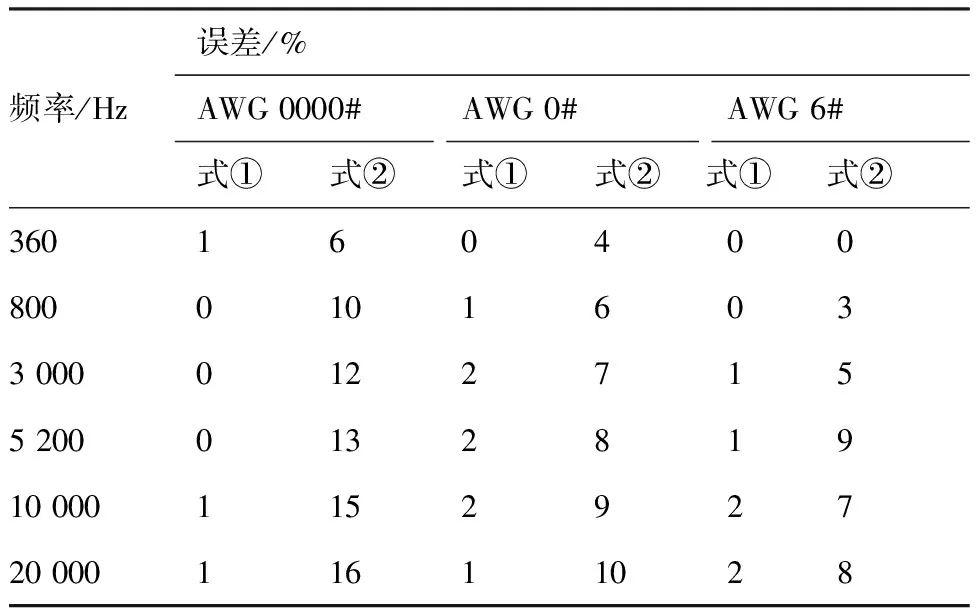
表1 两种计算方法误差分析Table 1 Error analysis of two calculation methods

注:式①代表式(12)计算结果，式②代表Payne公式计算结果。

3 交流电阻解析计算方法实验验证

借助已有的阻抗测量实验平台，验证两根导体交流电阻解析计算方法的正确性。测量用航空电缆导电面积为50 mm2，导体半径约为r=3.989 4 mm，绝缘层厚度为1.51 mm，外径为Rout=5.5 mm，导体间的中心距离为p=42 mm。使用可编程电源供电，所加电压为115 V，电流反向，频率在50～1 400 Hz内取几个典型测量点，线缆长为9.2 mm。实验测量平台如图15所示。

图15 阻抗测量实验平台Fig.15 Experiment platform for impedance measurement

实验测量电缆两端的电压降ΔV和实际所通电流I，根据两者的比值和相位差计算不同频率下的交流电阻值，得到实验测量值，记为R1；采用式(12)对实验中两根电缆的交流电阻进行理论计算，得到理论计算值，记为R2；借助有限元仿真软件ANSOFT对实验中的两根电缆进行仿真计算，可以得到仿真计算值，记为R3；实验测量值、理论计算值、仿真计算值的具体数值如表2所示。

将表2实验测量值、理论计算值和仿真计算值进行对比，如图16(a)所示。

从图16(a)中结果可以看出，两根电缆间交流电阻的实验测量值、理论计算值和仿真计算值三者随着频率变化的规律一致，均随着频率的增大而增大，并且三者之间的数值相差较小。接下来对其误差进行对比分析，对比结果如图16(b)所示。虚线是5%误差线。

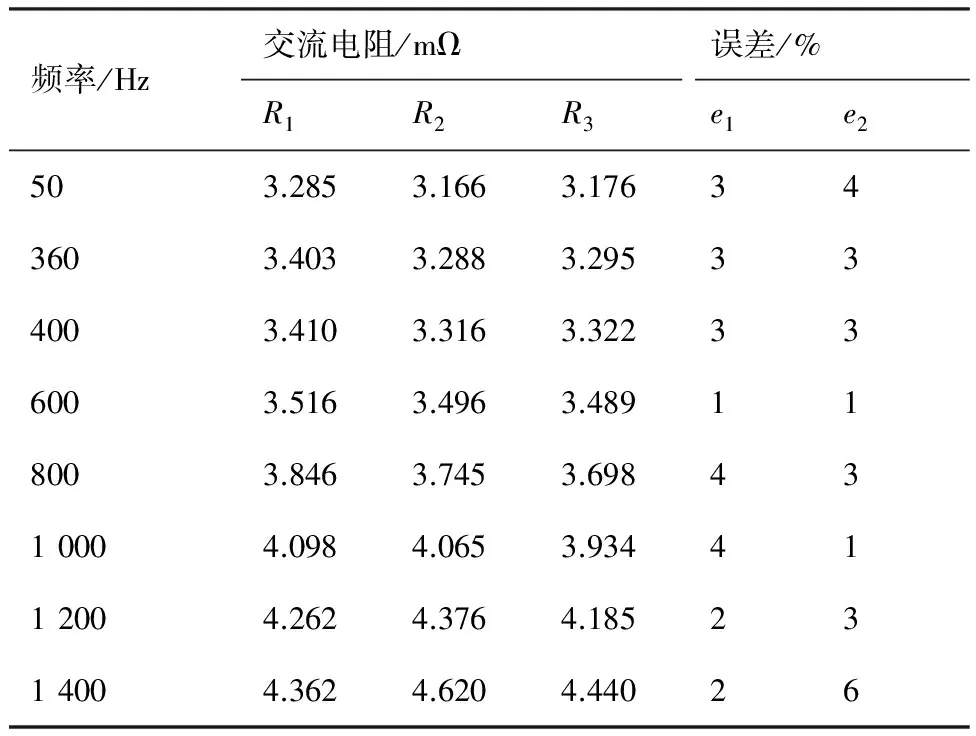
表2 两根电缆交流电阻值Table 2 AC resistance values of two cables

注：e1为仿真计算值和实验测量值之间的误差；e2为理论计算值和实验测量值之间的误差。

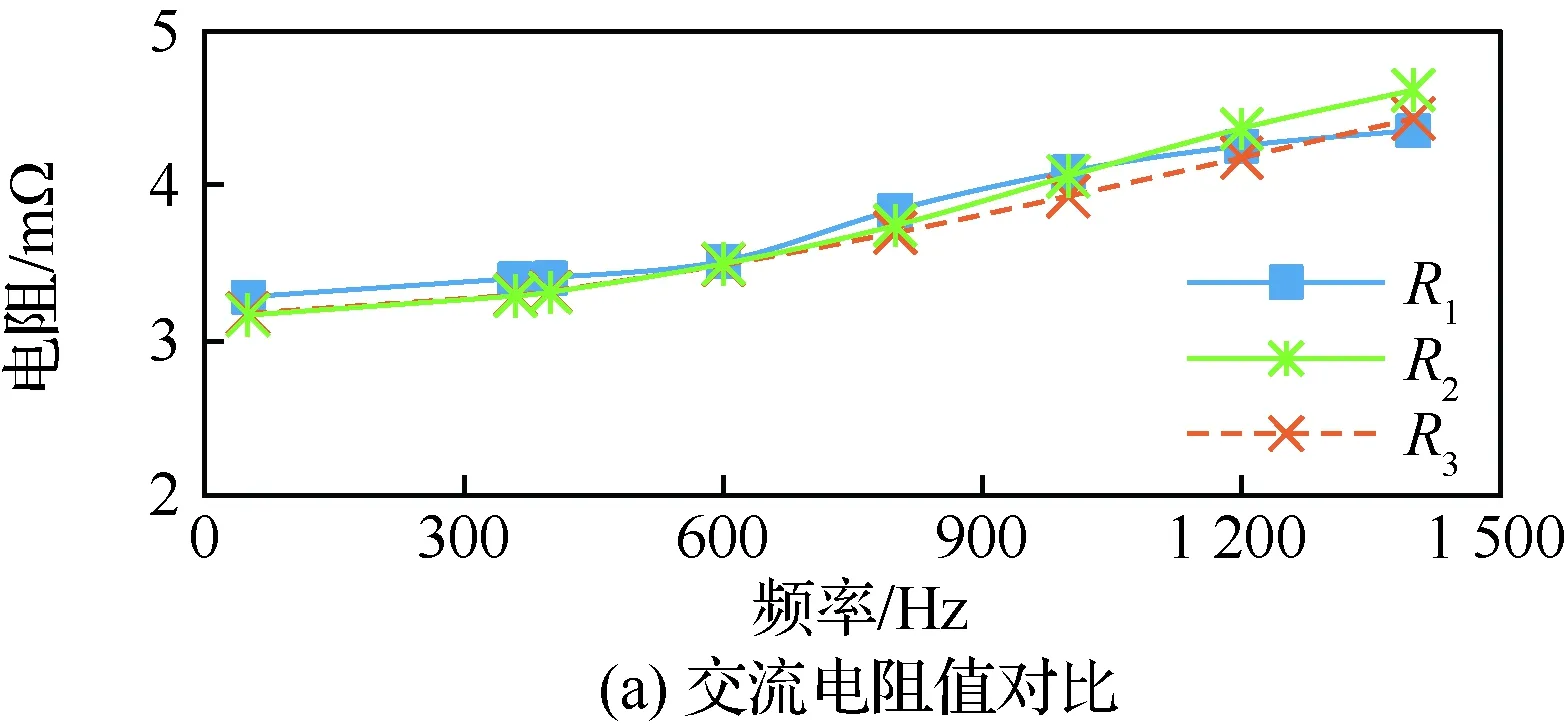
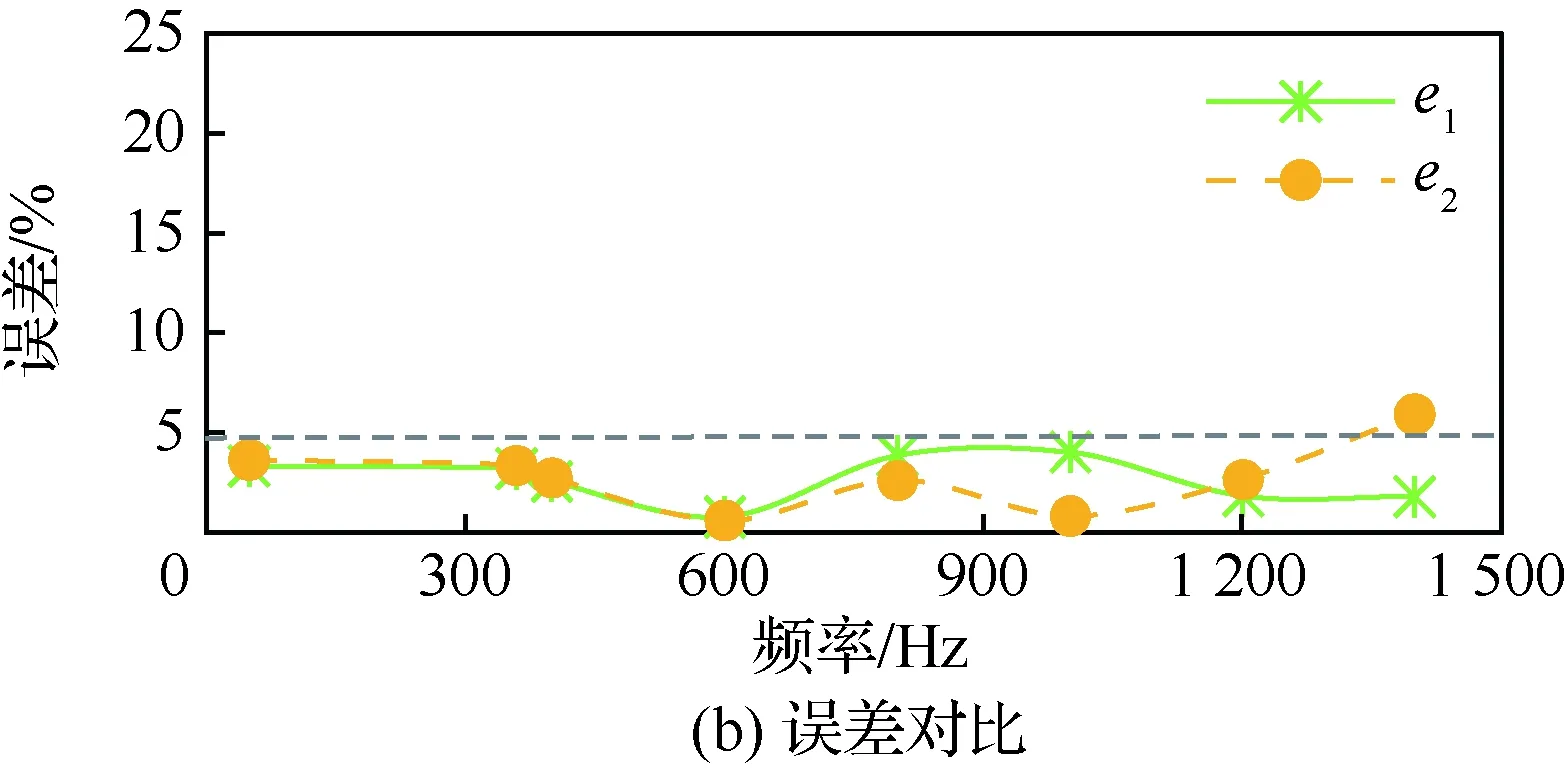
图16 两根电缆交流电阻值和误差曲线Fig.16 Curves of AC resistance value and error of two cables

从图16中的结果可以看出：① 仿真计算值与实验测量值之间的误差在4%以内，平均误差2.75%，证明了本文中所采用的有限元仿真建模方法的正确性，所求取的交流电阻值能够作为评估理论计算值的标准；② 理论计算值与实验测量值之间多数点误差在4%以内，平均误差3%，通过与实验测量值的对比，理论计算值的误差较小，说明本文给出的交流电阻解析计算方法能够很好地计算出两根导体间的交流电阻值，证明了交流电阻解析计算方法的正确性。

4 结 论

1) 推导并优化了两根导体间邻近因子的计算方法，将两根导体间交流电阻计算误差减小到5%以内。

2) 优化后的两根导体交流电阻解析计算方法具有适用范围广、计算过程简单、物理意义明确、计算精度高等优点，简化了繁琐的有限元仿真计算过程。

3) 为推导多导体主馈线敷设方式的交流电阻解析计算方法提供理论指导。

参 考 文 献

[1] HYVARINEN E W. Aircraft electric power system performance as affected by transmission line impedances[J]. IEEE Transactions on Aerospace and Electronic Systems, 1966, 2(4): 298-302.

[2] EDSON J H. Variable speed constant frequency (VSCF) electric power distribution systems for aircraft[J]. IEEE Transactions on Aerospace and Electronic Systems, 1966, 2(4): 290-297.

[3] 杨善水. 大型客机供电系统控制与管理关键技术研究[D]. 南京: 南京航空航天大学, 2011: 1-3.

YANG S S. The key technology research of large aircraft power supply system control and management[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 1-3 (in Chinese).

[4] 蔡林, 张玲, 杨善水, 等. 大型飞机供配电系统可靠性评估与分析[J]. 航空学报, 2011, 32(8): 1488-1496.

CAI L, ZHANG L, YANG S S, et al. Reliability assessment and analysis of large aircraft power distribution systems[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1488-1496 (in Chinese).

[5] 蔡梦迪. 大型飞机电源主馈线阻抗特性和敷设优化研究[D]. 南京: 南京航空航天大学, 2015: 1-2.

CAI M D. Research of wiring strategy optimization of main feeder in large aircraft power supply system based on impedance characteristic[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015: 1-2 (in Chinese).

[6] 祝家琪. 航空变频电源系统主馈线阻抗分析及布线方法研究[D]. 南京: 南京航空航天大学, 2013: 10-11.

ZHU J Q. Research of wiring strategy of main feeder in aircraft variable frequency power supply system based on impedance analysis[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013: 10-11 (in Chinese).

[7] ZHU J Q, WANG L, RUAN L G, et al. The skin effect and proximity effect analysis of main feeder of aircraft variable frequency AC system[C]∥Electrical Systems for Aircraft, Railway and Ship Propulsion (ESARS). Piscataway, NJ: IEEE Press, 2012: 1-6.

[8] 向念文, 陈维江, 李成榕, 等. 高铁信号系统多芯扭绞电缆宽频建模研究[J]. 中国电机工程学报, 2016, 36(2): 554-562.

XIANG N W, CHEN W J, LI C R, et al. Research onwideband modeling of multi-core twisted cables utilized for high-speed railway signaling systems[J]. Proceedings of the CSEE, 2016, 36(2): 554-562 (in Chinese).

[9] 吴新振, 王祥珩, 罗成. 异步电机转子感应非正弦电流时的导条损耗[J]. 中国电机工程学报, 2005, 25(17): 131-135.

WU X Z, WANG X H, LUO C. Loss calculation for induction machine rotor bar with non-sinusoidal current[J]. Proceedings of the CSEE, 2005, 25(17): 131-135 (in Chinese).

[10] KENNELLY A E, LAWS F A, PIERCE P H. Experimental researches on skin effect in conductors[J]. AIEE Transactions, 1915, 34(8): 1749-1814.

[11] PATEL U R, GUSTAVSEN B, TRIVERIO P. An equivalent surface current approach for the computation of the series impedance of power cables with inclusion of skin and proximity effects[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2474-2482.

[12] PAYNE A N. Skin effect, proximity effect and the resistance of circular and rectangular conductors[EB/OL], (2014-12-01)[2017-05-06]. http:∥g3rbj.co.uk/.

[13] 吴新振, 王祥珩. 异步电机双笼转子导条集肤效应的计算[J]. 中国电机工程学报, 2003, 23(3): 116-120.

WU X Z, WANG X H. Calculation of skin effect for double-cage rotor bar of the induction machine[J]. Proceedings of the CSEE, 2003, 23(3): 116-120(in Chinese).

[14] 旷建军, 阮新波, 任小永. 集肤和邻近效应对平面磁性元件绕组损耗影响的分析[J]. 中国电机工程学报, 2006, 26(5): 170-175.

KUANG J J, RUAN X B, REN X Y. Analysis of skin and proximity effects on winding losses in planar magnetic components[J]. Proceedings of the CSEE, 2006, 26(5): 170-175 (in Chinese).

[15] 严登俊, 刘瑞芳, 李伟. 有限公式法二维涡流场计算技术及其在电机集肤效应计算中的应用[J]. 中国电机工程学报, 2008, 28(9): 133-138.

YAN D J, LIU R F, LI W. Finite formulation computation technology for 2D eddy current field and application for skin effect in squirrel cage motor[J]. Proceedings of the CSEE, 2008, 28(9): 133-138 (in Chinese).

[16] 杜肖飞, 侯砚泽, 孙楚, 等. 航空变频电源下笼型感应电机矩形转子槽结构优化分析[J]. 航空学报, 2015, 36(2): 614-624.

DU X F, HOU Y Z, SUN C, et al. Optimization analysis of rectangular rotor slot of cage induction motor operating with areo variable frequency power[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 614-624 (in Chinese).

[17] 律方成, 郭云翔, 王彦旭, 等. 大功率中频变压器空心绕组交流电阻的计算方法[J]. 中国电机工程学报, 2016, 36(23): 6552-6559.

LV F C, GUO Y X, WANG Y X, et al. AC resistance calculation method for hollow conductor windings in high power medium frequency transformers[J]. Proceedings of the CSEE, 2016, 36(23): 6552-6559 (in Chinese).

[18] DWIGHT H B. Proximity effect in wires and thin tubes[J]. Transactions of the American Institute of Electrical Engineers, 1923, 42(9): 850-859.

[19] DWIGHT H B.Skin effect and proximity effect in tubular conductors[J]. American Institute of Electrical Engineers, 1922, 41(3): 203-209.

[20] 冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000: 44-45, 202-203.

FENG C Z, MA X K. Introduction to engineering electromagnetic field[M]. Beijing: Higher Education Press, 2000: 44-45, 202-203 (in Chinese).

[21] 薛太林, 吝伶艳. 电磁场[M]. 2版. 北京: 中国电力出版社, 2011: 200-203.

XUE T L, LIN L Y. Electromagnetic field[M]. 2nd ed. Beijing: China Electric Power Press, 2011: 200-203 (in Chinese).