考虑开路运行模式时的五相永磁同步电机FOC

葛 蔷,田 兵,孙 力,安群涛,赵 克

(哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150001)

0 引言

五相永磁同步电机的突出优点之一是容错运行。开路故障下,维持剩余相的相电流形成圆形旋转磁势即可保证五相电机无扰运行。通常三相交流电机发生开路故障时,需改变电机和逆变器的硬件拓扑结构(重新连接三相电机中性线和直流母线中点);而五相电机由于较多的相自由度,容错控制非常方便,控制剩余相的相电流即可实现无扰运行[1-2]。

逆变器与电机绕组之间的开路故障是一种常见的故障类型[3];同时为了防止电机过热/过流引起永磁体失磁,电机绕组和逆变器短路故障也将被转换成开路故障处理[4]。因此对于故障模式下的电机控制,大多数学者的研究集中在开路运行模式下的容错控制[5-6]。对于五相电机容错控制策略,现有文献较多地研究如何重构剩余相的相电流,达到电磁转矩平稳输出的目的。由于开路故障下电流重新分配是一个多解问题,为了达到最优的控制目的,需要附加约束条件,如总体铜损损耗最小、相电流等幅值、转矩纹波最小等,以此便可计算出上述代价函数下的最优相电流解[1,7-8]。根据现有文献,电流重构方法可以划分为:通过维持定子磁动势相对于正常模式时不变,约束相电流取值范围[9-10];剩余相的相电流在空间上关于故障相镜像对称,根据机械和电磁瞬 时功率平衡并以输出最大转矩为约束条件[11]。在开路模式下,相电流重新分配依赖于电机模型参数,因此多数文献采用离线计算方法重构相电流,同时采用电流滞环控制驱动故障电机[7,12-14]。

由于开关频率不固定,滞环电流控制并不是一种理想的电机驱动方案。在工业应用场合,同步旋转PI调节器及脉宽调制(PWM)方法是一种广泛应用的电机控制策略[15]。采用转子磁场定向控制FOC(Field Oriented Control),位置耦合的电机模型通常可以简化为线性模型,而相电流则解耦为转矩控制成分和弱磁控制成分,因此交流电机可以等效为独立励磁的直流电机[2,16-17]。为了在开路运行模式下采用FOC,文献[18]认为开路故障是一种特殊形式的扰动,通过智能控制,正常模式下的FOC在开路模式下获得了成功应用。此外,文献[15]提出在新的旋转坐标系下进行单相开路模式下的FOC,通过降阶Clarke和Park变换矩阵实现了电流在同步旋转坐标系下的重新分配。相比于相坐标系下的电流配置,文献[15]方法可以实现故障电流在旋转坐标系下的在线计算,然而所提出的Clarke和Park变换矩阵并未实现故障电机模型空间位置解耦,因此不适合采用旋转PI电流调节器。除此之外,为了提高开路运行模式下电机降额率,文献[19]采用五相全桥逆变器和电机开绕组运行模式,以达到相电流独立控制的目的;但是采用全桥结构的电机驱动系统不仅变得更加脆弱,而且容错控制时对电机参数也有一定的要求,即要求电机相间低互感以忽略磁阻转矩。就提高五相电机的可靠性而言,半桥逆变器和星形连接的电机是一种合理的搭配。

为了在开路运行模式下采用FOC和PWM策略,本文将五相电机正常运行模式时的FOC进行了扩展,基于维持定子磁动势和定子磁链圆形旋转的原则,提出了分别适用于单相开路、两相开路(包括相邻两相和不相邻两相开路)模式下的FOC;同时给出了考虑梯形波反电动势的解耦电压方程和转矩方程。由于三相开路模式下电机降额率严重且需额外添加零序控制电路,因此不在本文研究范围之内。本文解耦后的电机解析模型表明,在开路运行模式下,故障电机的控制完全可以媲美正常模式下的矢量控制,因此FOC可以拓展到开路故障模式中,其数字控制实现也得到进一步简化。通过五相电机驱动系统验证了所提出的空间解耦模型以及FOC的有效性。

1 正常模式下的五相电机解耦建模方法

对于星形连接的五相电机,正常模式下,其相坐标下的模型通常被分解为2个正交子空间:基波旋转空间和3倍频旋转空间。基波定子磁动势可以表示为[20-21]:

(1)

其中,F为基波定子磁动势;N为绕组匝数;I为基波励磁电流;γ=ejδ,δ为相邻相之间的空间偏移角,δ=2π/5;ω为电机转速;iA、iB、iC、iD、iE为五相电机的相电流。

同样,3次谐波定子磁动势为:

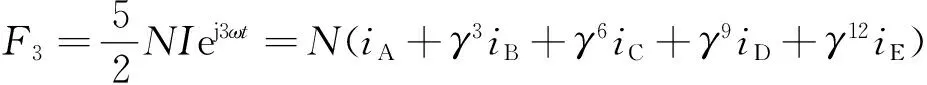
(2)

其中,F3为3次谐波定子磁动势。

通过上述约束,配置相电流形成圆形旋转定子磁动势,可得到两相静止坐标下的电流表达式:

(3)

其中,iα和iβ、iα3和iβ3、io分别为相电流在基频、3倍频及零序空间的投影;δ=2π/5。等式左边的矩阵便为适用于五相电机正常模式下的Clarke矩阵。

2 开路模式下的五相电机建模方法

在开路故障下,故障相电流恒为0。如果剩余相的相电流仍通过上述Clarke变换,得到的α-β平面电流相轨迹将不能维持圆形旋转。因此需要重构相电流,达到开路模式下机电能量平稳传输的目的。本文基于维持定子磁动势圆形和定子永磁体磁链圆形旋转这一原则(约束条件)来配置相电流。

在正常模式下,通过扩展Clarke矩阵约束基波和3次谐波定子磁动势圆形旋转,即可得到相电流解,同时交链于每相的永磁体磁链在α-β平面也将保持圆形旋转,既永磁体磁链在α-β平面可以表示为[20-21]:

(4)

(5)

其中,ψm-α、ψm-β为α-β平面下的各相永磁体磁链;ψm-A、ψm-B为交链于每相的基波永磁体磁链;ψm为永磁体磁链幅值;θ为转子位置。

借鉴式(4)方法,在开路模式下基波定子磁动势和永磁体磁链的相轨迹可维持圆形旋转。由于3次谐波分量在故障模式下并不承担能量传输,因此在推导适用于开路模式下的Clarke和Park矩阵时,暂且不考虑3次谐波分量。

2.1 单相开路故障下解耦建模方法

不失一般性,假设A相发生开路故障。同时认为永磁体磁密不受温度、齿槽、磁饱和效应等因素影响。剩余相电流可重新配置来维持故障前后基波定子磁动势不变,因此有:

(6)

其中，iA≡0。考虑五相电机星形绕组连接,其零序电流恒为0,因此式(6)可被进一步改写为:

(7)

五相电机在星形绕组连接下没有零序电流,因此式(7)不适用于开放绕组连接的电机。又因式(7)中矩阵的第三行矢量与其他矢量均不正交[15],故可将第三行移除并且在第一行和第二行分别添加修正因子x、y,得到如下矩阵:

(8)

其中,i3为3次谐波空间脉振电流。星形连接下,上述关系式满足零序电流恒为0的约束条件:

x(iB+iC+iD+iE)≡0,y(iB+iC+iD+iE)≡0

(9)

因此单相开路下剩余相在α-β平面所产生的永磁体磁链分别为:

cos(4δ)ψm-E]-0.4x(ψm-B+ψm-C+ψm-D+ψm-E)=ψmcosθ|x=1

(10)

sin(3δ)ψm-D+sin(4δ)ψm-E]=

ψmsinθ|y=0

(11)

其中,磁链符号中的上标“A”表示A相(单相)开路故障。由式(10)和(11)可以看出经过修正后的基波空间永磁体磁链相轨迹保持圆形旋转。因此适用于单相开路故障下的五相电机Clarke变换矩阵可以写为:

(12)

2.2 相邻两相开路故障下解耦建模方法

参考单相开路下的电流配置方法,假设开路相为相邻A和B两相,为保证容错控制,剩余相电流仍通过维持故障前后基波定子磁动势不变原则，有:

(13)

其中，iA≡0；iB≡0。将式(13)进一步改写为:

(14)

上式成立需考虑如下零序电流约束条件:

x(iC+iD+iE)≡0,y(iC+iD+iE)≡0

(15)

剩余相的永磁体磁链在α-β平面的投影为:

cos(4δ)ψm-E]-0.4x(ψm-C+ψm-D+ψm-E)=

ψm-α-0.4(ψm-A+cosδψm-B)+

0.4x(ψm-A+ψm-B)

(16)

sin(4δ)ψm-E]-0.4y(ψm-C+ψm-D+ψm-E)=ψm-β-0.4(ψm-A+sinδψm-B)+

0.4y(ψm-A+ψm-B)

(17)

其中,磁链符号中的上标“AB”表示A、B相(相邻两相)开路故障。由式(16)和(17)可以看出当x=0、y=0(即不进行Clarke矩阵修正)时,A、B相邻两相开路故障下α-β平面永磁体磁链无法圆形旋转,机电能量也不能进行平稳传输。因此,可利用脉振的零序空间分量来修正永磁体磁链的相轨迹,并使其进行圆形旋转。令:

(18)

可得:

(19)

因此重新定义A、B相邻两相开路模式下的五相电机Clarke变换矩阵:

(20)

2.3 不相邻两相开路故障下解耦建模方法

基于同样的方法,假设开路相为不相邻A、C两相,仍通过维持故障前后基波定子磁动势不变,有:

(21)

其中，iA≡0；iC≡0。进一步将式(21)改写为:

(22)

剩余相永磁体磁链在α-β平面投影分别为:

0.4x(ψm-B+ψm-D+ψm-E)=ψm-α-0.4[ψm-A+

cos(2δ)ψm-C]+0.4x(ψm-A+ψm-C)

(23)

0.4y(ψm-B+ψm-D+ψm-E)=ψm-β-0.4[ψm-A+

sin(2δ)ψm-C]+0.4y(ψm-A+ψm-C)

(24)

同样令:

(25)

可得:

x=cos(2δ),y=tanδcos(2δ)
k=0.6+0.4cosδ

(26)

其中,磁链符号中的上标“AC”表示A、C相(不相邻两相)开路故障。通过此方法修正后的基波永磁体磁链相轨迹圆形旋转,因此可以平稳地进行机电能量传输。因此不相邻两相开路故障下的五相电机Clarke变换矩阵可以重新定义为:

(27)

3 五相电机解耦建模方法

开路模式下电机本身并未遭到破坏,因此仍可以采用正常状态的电压方程描述故障电机,五相永磁同步电机在自然坐标系下的电压方程为[2,6]:

(28)

其中,uA、uB、uC、uD、uE为五相电机端电压,由五相电压型半桥逆变器供电;Rs为五相电机相电阻;电感矩阵中对角线位置上的元素表示自感,非对角线位置表示为互感;d/dt表示微分运算符。值得注意的是,上述电感矩阵考虑了漏感以及转子位置耦合电感,其表达式可参考文献[6]。当某相发生开路故障时,由于该相的相电流恒等于0,因此将不再受逆变器调节控制。考虑上述情况,正常模式下的电压方程可以进行降阶处理,即忽略上述电压方程中的故障相对应的电感或磁链表达式。

因此,将相坐标系下电压方程表示为:

(29)

将上述相坐标系下的电压方程转换到dq旋转坐标系下得:

(30)

Udq=TParkTClarkeUs,Idq=TParkTClarkeIs

(31)

需要注意的是,不同模式(正常、单相开路、两相开路)下Park变换矩阵也有所不同。适用于这些模式下的Park 矩阵分别描述如下:

(32)

电磁转矩方程式可由磁共能对位置求偏导获得[2,6],表示为:

(33)

其中,Te为电磁转矩;Wco为磁共能;p为五相电机极对数。

将正常模式、单相开路、两相开路下的Clarke、Park矩阵代入上述电压方程和转矩方程,即对五相电机进行解耦建模,分别得到正常运行、单相开路和两相开路(包含相邻两相和不相邻两相开路故障)运行模式下的五相电机在dq旋转坐标系下的电压方程和转矩方程。

正常模式下五相电机解耦模型为:

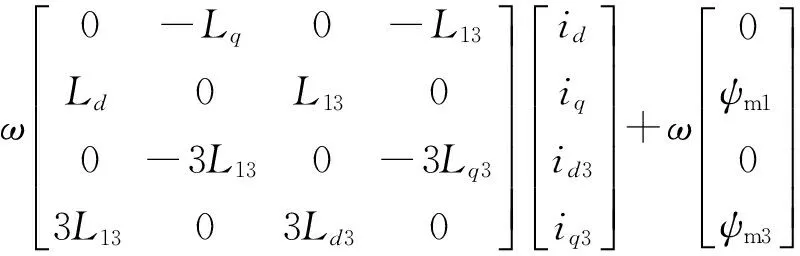
(34)

(35)

其中,L13为基波空间和3次谐波空间互感,Ld、Lq、Ld3、Lq3分别为基波旋转坐标系和3倍频旋转坐标系下的直轴、交轴电感,其表达式可参考文献[20-21];id、iq分别为dq旋转坐标系下的直轴、交轴电流;ψm1、ψm3分别为dq旋转坐标系下的基波和3次谐波永磁体磁链。

单相开路故障下五相电机解耦模型为:

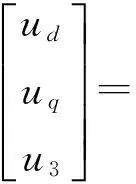
(36)

(37)

其中,Lls为漏感。值得注意的是,在开路模式下Ld和Lq保持一致,因此本文并没有在电感符号上标注上标加以区别。

两相相邻开路下五相电机解耦模型简化为:

(38)

(39)

同理,不相邻两相开路下故障电机模型为:

(40)

(41)

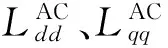
从正常、单相开路和两相开路(相邻和不相邻两相开路)模式下解耦模型可以看出,用来维持能量传输的基波空间的电压方程和转矩方程均有非常类似的结构,其控制完全可以媲美三相交流电机。因此可以采用FOC,利用旋转PI调节器控制相电流。然而本实验平台的五相电机反电动势为梯形波反电动势,在开路故障下3次谐波成分在α-β平面是脉振的,并且与基波电流作用产生脉振的转矩。因此本文为了减小电磁转矩纹波,统一采用id=0控制。

考虑id=0控制,单相开路故障下谐波转矩(由基波电流和谐波磁链部分产生)为:

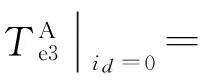
(42)

相邻两相开路故障下谐波转矩为:

(43)

不相邻两相开路故障下谐波转矩为:

(44)

4 实验结果

在五相电机驱动平台上,对FOC进行了验证。采用五相半桥逆变器控制五相电机,直流电机作为负载。控制器采用DSP+FPGA模式,其中DSP完成控制算法(电流闭环控制或转速控制),FPGA完成Clarke和Park矩阵(包括逆变换)以及PWM。DSP通过并行数据口发送控制指令可以切换到其他故障(或正常)模式下的FOC,而DSP中电流控制统一采用同步旋转PI调节器。五相电机FOC系统框图如图1所示,其中根据开路相数,Clarke和Park以及其逆矩阵将会有所不同,可参考式(3)、(12)、(20)、(27)和(32)。 IGBT模块的开关频率为10.30 kHz,电机转动惯量为0.33 kg/m2。

图1 五相电机FOC控制系统框图Fig.1 Block diagram of five-phase motor control system

图2 统一FOC下的五相电机相电流Fig.2 Phase currents of five-phase motor with proposed unified FOC

图2为正常模式、单相开路模式、两相开路模式下采用FOC时的相电流控制波形。其中FOC统一采用id=0、iq=constant。图2(a)为正常模式下的相电流,该电流基本正弦,并将其作为参考波形用来对比开路情况下id=0控制时的电流输出。图2(b)和(c)均为单相开路故障模式下的相电流波形。其中,图2(b)为单相开路模式下的相电流等幅值控制,通过此约束条件,容易求得dq旋转坐标系下电流分配情况为id=0、iq=constant、i3=0.236iqcosθ;图2(c)为单相开路模式下的总体铜损最小控制,此时dq旋转坐标系下电流分配将服从id=0、iq=constant、i3=0。图2(d)和(e)分别为相邻两相和不相邻两相发生开路时的相电流,dq旋转坐标系下电流分配服从id=0、iq=constant。从单相开路和两相开路故障下的电流波形可以看出,采用统一id=0控制,故障模式下电流波形基本达到了正弦,相电流幅值随着开路相数的增加呈现增加趋势,这是由于故障模式下电机需要较多的定子电流,以维持等同的定子磁动势。由于3次谐波绕组的存在,部分谐波电流无法通过旋转PI调节器得到抑制,因此造成图2(e)相电流出现一定程度的失真。谐波电流可通过自适应多谐振控制器以及基于模型的控制算法予以抑制,本文对此不作具体研究。

图3 统一FOC下的五相电机αβ坐标系电流Fig.3 Currents of five-phase motor under αβ frame with proposed unified FOC

图3为正常模式、单相开路模式、两相开路(包括相邻和不相邻)模式下采用FOC时αβ坐标系下电流控制波形、转速及转子位置波形。图3(a)为正常模式下的电流、转速和转子位置波形,这些波形将作为参考波形,与开路情况下id=0控制时电流、转速和转子位置波形做对比。图3(b)和(c)均对应单相开路运行模式电流波形,可以看出αβ坐标系下电流呈现正交且等幅值,和正常模式下保持一致,这说明单相开路故障下定子磁动势可维持不变。图3(d)和(e)对应两相开路运行模式,其定子磁动势亦可维持不变。同时,从转速波形可以看出,随着开路相数的增加,转速纹波亦变得较为强烈,转速纹波由转矩纹波造成,或者说由3次谐波绕组引起。因此,采用正弦波分布绕组可从根本上解决故障运行模式下的转矩波动。

图4 统一FOC下的五相电机dq坐标系电流Fig.4 Currents of five-phase motor under dq frame with proposed unified FOC

图4为正常模式、单相开路模式和两相开路模式下采用FOC时dq旋转坐标系下电流控制波形以及转子位置波形。图4(a)为正常模式下的电流、转子位置波形,这些波形将作为参考波形,与开路情况下id=0控制时电流、转速和转子位置波形做对比。图4(b)和(c)均对应单相开路运行模式电流波形,图4(c)采用电流等幅值控制方式,体现在i3电流出现脉振。而在两相开路故障时,剩余3相的相电流解耦为dq旋转坐标系下2路直流电流,因此图4(d)和(c)在dq旋转坐标系下的电流控制可以高度统一。同时,从各模式下的交、直轴电流可以看出,当采用id=0控制时,产生同样大小的电磁转矩需要的iq电流也保持一致。因此开路运行模式下的FOC完全可以媲美三相交流电机矢量控制,并且和五相电机正常运行模式进行统一,这大幅简化了五相电机的容错控制,增强了电机运行的可靠性,同时也有利于故障电机调速控制。

5 结论

通过维持剩余相所形成的定子磁动势和定子磁链圆形旋转,提出了五相永磁同步电机在单相开路和两相开路(相邻和不相邻)模式下的空间解耦模型。这些解耦模型和正常模式下的五相电机在dq旋转坐标系的模型具有相似的电压方程和转矩方程,因此矢量控制可以得到统一。在五相电机驱动系统上验证了统一FOC在正常运行、单相开路和两相开路运行模式下的有效性。本文所提方法的意义在于:故障电机电流可以在dq旋转坐标系下在线配置,同时可采用PWM方法;开路模式下空间解耦模型可为依赖模型的先进算法的实现提供了可能,如直接转矩控制、无位置传感器控制技术等。

参考文献：

[ 1 ] GUZMAN H,DURAN M J,BARRERO F,et al. Comparative study of predictive and resonant controllers in fault-tolerant five-phase induction motor drives[J]. IEEE Transactions on Industrial Electro-nics,2016,63(1):606-617.

[ 2 ] TIAN B,AN Q,DUAN J,et al. Cancellation of torque ripples with FOC strategy under two phase failures of five-phase PM motor[J]. IEEE Transactions on Power Electronics,2017,32(7):5459-5472.

[ 3 ] ZHANG X,WANG Y,LIU G,et al. Robust regenerative charging control based on T-S fuzzy sliding-mode approach for advanced electric vehicle[J]. IEEE Transactions on Transportation Electrification,2016,2(1):52-65.

[ 4 ] TOLIYAT H A. Analysis and simulation of five-phase variable-speed induction motor drives under asymmetrical connections[J]. IEEE Transactions on Power Electronics,1998,13(4):748-756.

[ 5 ] SALEHIFAR M,ARASHLOO R S,MORENO-EQUILAZ J M,et al. Fault detection and fault tolerant operation of a five phase PM motor drive using adaptive model identification approach[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2014,2(2):212-223.

[ 6 ] TIAN B,AN Q,DUAN J,et al. Decoupled modeling and nonlinear speed control for five-phase PM motor under single phase open fault[J]. IEEE Transactions on Power Electronics,2017,32(7):5473-5486.

[ 7 ] LIU G,QU L,ZHAO W,et al. Comparison of two SVPWM control strategies of five-phase fault-tolerant permanent-magnet motor[J]. IEEE Transactions on Power Electronics,2016,31(9):6621-6630.

[ 8 ] BARIK S K,JALADI K K. A comparative analysis of different conduction modes in VSI with five phase induction motor[C]∥International Conference on Microelectronics,Computing and Communications. New Jersey,USA:IEEE,2016:1-6.

[ 9 ] 康敏,孔武斌,黄进. 电动汽车用五相感应电机容错控制[J]. 电机与控制学报,2014,18(3):1-6.

KANG Min,KONG Wubin,HUANG Jin. Fault-tolerant control of five-phase induction motor for electric vehicles[J]. Electric Machines & Control,2014,18(3):1-6.

[10] ABDEL-KHALIK A S,ELGENEDY M A,AHMED S,et al. An improved fault-tolerant five-phase induction machine using a combined star/pentagon single layer stator winding connection[J]. IEEE Transactions on Industrial Electronics,2016,63(1):618-628.

[11] MOHAMMADPOUR A,PARSA L. A unified fault-tolerant current control approach for five-phase PM motors with trapezoidal back EMF under different stator winding connections[J]. IEEE Transactions on Power Electronics,2013,28(7):3517-3527.

[12] 高宏伟,杨贵杰,刘剑. 五相永磁同步电机容错控制策略[J]. 电机与控制学报,2014,18(6):61-65.

GAO Hongwei,YANG Guijie,LIU Jian. Fault-tolerant control strategy for five-phase permanent magnet synchronous motor[J]. Electric Machines & Control,2014,18(6):61-65.

[13] 赵品志,杨贵杰,李勇. 五相永磁同步电动机单相开路故障的容错控制策略[J]. 中国电机工程学报,2011,31(24):68-76.

ZHAO Pinzhi,YANG Guijie,LI Yong. Fault-tolerant control strategy for five-phase permanent magnetic synchronous motor under single phase open-circuit fault condition[J]. Proceedings of the CSEE,2011,31(24):68-76.

[14] MOHAMMADPOUR A,SADEGHI S,PARSA L. A generalized fault-tolerant control strategy for five-phase PM motor drives considering star,pentagon,and pentacle connections of stator windings[J]. IEEE Transactions on Industrial Electronics,2014,61(1):63-75.

[15] RYU H M,KIM J W,SUL S K. Synchronous frame current control of multi-phase synchronous motor-part Ⅱ asymmetric fault condition due to open phases[C]∥39th IAS Annual Industry Applications Confe-rence. Seattle,USA:IEEE,2004:275.

[16] TOLIYAT H A,WAIKAR S P,LIPO T A. Analysis and simulation of five-phase synchronous reluctance machines including third harmonic of airgap MMF[J]. IEEE Transactions on Industry Applications,1998,34(2):332-339.

[17] SEMENOV D,AN Q,SUN L,et al. Nonlinear speed control for five-phase PMSM in electric vehicles[C]∥Power Engineering Confe-rence. Brisbane,Australia:IEEE,2016:1-5.

[18] LIN F J,HUNG Y C,TSAI M T. Fault-tolerant control for six-phase PMSM drive system via intelligent complementary sliding-mode control using TSKFNN-AMF[J]. IEEE Transactions on Industrial Electronics,2013,60(12):5747-5762.

[19] BIANCHI N,BOLOGNANI S,PRE M D,et al. Post-fault operations of five-phase motor using a full-bridge inverter[C]∥IEEE Power Electronics Specialists Conference. Rhodes,Greece:IEEE,2008:2528-2534.

[20] RYU H M,KIM J W,SUL S K. Synchronous frame current control of multi-phase synchronous motor. part I. modeling and current control based on multiple D-Q spaces concept under balanced condition[C]∥39th IAS Annual Industry Applications Conference. [S.l.]:IEEE,2004:63.

[21] SHI R,TOLIYAT H A. Vector control of five-phase synchronous reluctance motor with Space Vector Pulse Width Modulation(SVPWM) for minimum switching losses[C]∥Applied Power Electronics Conference and Exposition. Texas,USA:IEEE,2002:57-63.