基于改造粒子群游的超高压故障限流器全局优化配置算法

应林志，刘天琪，王建全

(1. 四川大学 电气信息学院，四川 成都 610065；2. 浙江大学 电气工程学院，浙江 杭州 310058)

0 引言

现代电网规模日益扩大、互联程度越来越高，使得短路故障电流水平不断升高，已成为限制电网持续健康发展的主要问题之一[1-4]。传统分区分层等限制短路电流的措施大多需要牺牲系统可靠性，难以满足日益高涨的供电保障要求。故障限流器FCL(Fault Current Limiter)在正常状态下对电网无影响，而在电网发生短路时可迅速触发投入限流电抗，有效限制短路电流，从而确保故障可靠断开，能较好地解决限流与系统可靠性之间的矛盾[5]。

超高压电网作为承担主要输电任务的骨干网络，面临可靠性要求高、限流需求大之间的矛盾更加突出的问题，这为故障限流器提供了广阔的应用前景。针对电网具体情况，优化故障限流器的关键是适当的数量、阻抗和选点配置。文献[6]采用解析法达成限流目标，但经济性有所不足。文献[7]未限制可行解空间，导致粒子群规模偏大，优化效率略有欠缺。文献[8]将多目标变为单目标优化问题，实现简单、收敛迅速，但全局寻优能力欠佳、难以确保达成限流效果。文献[9]采用非支配排序遗传算法，但易破坏种群多样性，优化结果不稳定。文献[10]采用经局部差分原理改进的非支配排序遗传算法，文献[11]综合考虑故障限流器成本和限流效果采用改进免疫算法，问题在于计算规模上升将对效率产生较大的影响。鉴于超高压故障限流器造价高昂，应力求以最少数量和最低单台成本满足全局限流需求。以适当方法因地制宜地区分短路电流主要路径，高效搜索满足预设限流目标、经济代价最小的故障限流器配置方案具有十分重要的意义。

本文考虑超高压故障限流器在大电网中的应用特点，以获取预设全局限流效果和确保配置最优经济性为目标，基于邻接转移阻抗灵敏度NTIS(Nearby Transfer Impedance Sensitivity)加权值，提出一种能够区分短路电流关键路径、反映限流经济代价、指示全局限流效果及均衡水平的适应函数，作为全局限流效果衡量指标。将故障限流器装设数量、单台阻抗及布点配置视为大规模混合整形优化问题，在基本粒子群游智能优化PSO(Particle Swarm Optimization)的基础上，根据故障限流器的应用特点对解编码、位移操作等方面进行改造，引入灵敏度排序降维、追加支路法简化中间计算量，形成了一种故障限流器配置问题的全局优化算法(以下简称RPSO-NTIS算法)，并以不同规模算例测试验证了该算法的有效性。

1 故障限流器优化配置数学模型

根据超高压故障限流器的应用特点，不同结构、形式、种类的故障限流器的基本工作原理基本一致，即在系统正常运行时表现为零阻抗或微小阻抗，在发生短路故障时迅速呈现高阻抗限制短路故障电流。因此，无论是电力电子型还是新型材料故障限流器，其优化配置问题均可视为在目标电网内选取部分超高压输电线路加装故障限流器，以达到预定的限流目标，例如使所有超高压站点保持一定的短路电流裕度。优化配置问题的解为故障限流器数量、限流电抗成本以及安装选点，为最经济安全、准确高效地达成限流目标，需要选取科学的适应函数以衡量全局限流效果及其经济性。

对于超高压电网而言，三相短路通常是最严重的短路故障类型。为确保可靠隔离保短路故障，一般采用节点母线三相短路电流水平来确定相关断路器遮断电流水平。从工程应用角度，分析基于转移阻抗的短路电流计算原理[12-14]，易知电源节点对需要限流节点贡献的故障电流分量与其间转移阻抗呈反比。

首先定义当有m台故障限流器达到启动条件而投入限流电抗后，发电机节点r与邻接节点i间的转移阻抗灵敏度为ηri，见式(1)。

(1)

(2)

然后，定义需限流节点k的邻接节点转移阻抗增量灵敏度加权和为φk：

(3)

其中，εk=(Ik-Ibk)/Ibk，为故障限流器未启动时反映需限流节点k的短路电流大小的加权系数，Ik、Ibk分别为节点k的短路电流和遮断电流；εi=Iik/Ik，为故障限流器未启动时反映邻接节点i提供的短路电流分量Iik大小的加权系数；εri=Iri/Iik，为故障限流器未启动时反映发电机节点r对邻接节点i提供的短路电流分量Iri大小的加权系数；Nnext为当前需要限流节点对应的邻接节点数目；NG为系统发电机节点数。

(4)

将确保经济成本最低、全局限流效果达标等多目标融合为单目标寻优问题，有利于优化算法提升计算效率。为研究区分各电源节点提供短路电流分量的路径，甄别邻接节点对需限流节点的短路电流贡献值，寻求综合最优限流效果，结合安装故障限流器成本的经济性，本文将故障限流器优化配置问题数学模型描述为基于NTIS的适应函数η，计算见式(5)，需限流节点k的邻接转移阻抗示意图见图1。

(5)

其中，ZFCLp为第p台故障限流器的限流电抗值；NFCL为安装的故障限流器数量；a为限流电抗成本系数，由于超高压故障限流器等效电抗与单位成本之间为非线性关系，本文设置a=bZFCLp，b为不大于1的常数。

图1 邻接转移阻抗示意图Fig.1 Schematic diagram of nearby transfer impedance

适应函数η反映安装多台故障限流器后对大电网可产生的全局综合限流效果，并兼顾故障限流器数量、限流电抗值以及短路电流提供路径。η越大，对短路电流贡献值高的电源节点以及短路点邻接节点的限制越大，安装的故障限流器总成本越小，确保了优化配置结果的有效性和经济性，因此应在全局寻优中找到该适应函数的极大值。

2 基于改造粒子群游的超高压故障限流器全局优化配置算法

2.1 超高压故障限流器配置问题的PSO建模改造

故障限流器配置问题的解包含选点和选型(限流电抗大小)2个离散变量，PSO能很好地解决这类优化问题[15-19]。为进一步提高算法的搜索性能和适应度，针对故障限流器配置问题重新对算法进行建模改造。

2.1.1 目标引导函数

设定目标引导函数为搜索η的极大值，见式(6)。

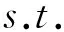
(6)

针对故障限流器选点和选型特性，采用二进制编码，构建双轨编解码模型，粒子的位置向量S表示为2个编码序列的组合。

(7)

其中，X为选点解编码序列，元素xi=1表示线路i安装故障限流器，xi=0表示线路i未安装故障限流器；Y为选型解编码序列，yj为整实数，表示第j台已安装故障限流器的选型编号，对应预先设定的限流电抗数组元素；Nallowed为允许装设故障限流器的支路数；Ninstall为装设故障限流器的数量。我国华东电网已有超高压故障限流器投运并发挥作用的成功案例，本文中故障限流器参考其动作条件[20]。

算法输出的故障限流器优化配置方案，须满足以下约束条件。

a. 潮流约束：本文设定潮流迭代超过100次即不满足潮流约束条件。

b. 支路潮流约束：Si≤Si,max，Si、Si,max分别为支路i的首端功率及上限允许值。

c. 节点电压约束：Ui,min≤Ui≤Ui,max，Ui和Ui,max、Ui,min分别为节点i的电压和节点电压上、下限。

d. 限流目标约束：Ii≤Ii,max，Ii、Ii,max分别为需限流节点i的短路电流、限流目标对应的短路电流上限。

e. 暂态安全约束：确保故障限流器正常投切、投入限流电抗后无法切除、故障长时间串入限流电抗等各种条件下不会引起系统电压失稳或功角失稳。

若同时满足上述约束条件并达成预设限流目标，则认为输出方案为推荐方案。

2.1.2 交换操作的基本定义

a. 交换子：设当前解为S=(X,Y)，定义交换子SOX(i1,i2)为交换解S的序列X中的元素xi1和xi2，经上述交换子操作后得新解S′=S+SOX(i1,i2)。对序列Y的操作同上。

b. 交换序：若干交换子的有序队列，记作SS。

(8)

c. 交换序合并算子⊗：交换序SS1和SS2先后作用于S，得到新解S′，若交换序SS′作用于S可得相同的S′，则SS′=SS1⊗SS2。

d. 基本交换序：作用于同一解产生相同新解的交换序中，交换子数量最少的交换序。

2.1.3 粒子速度更新公式的重构

将粒子个体速度和位置更新公式重构为式(9)，其适用于故障限流器选点和选型。

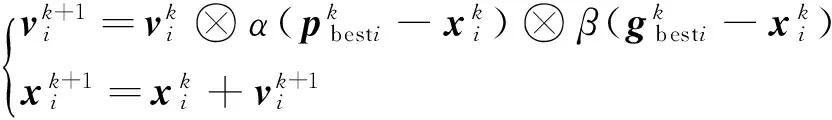
(9)

为防止粒子群在迭代过程中出现早熟、过快收敛至局部最优解，本文借鉴遗传算法思想，首先按式(10)生成随机概率ε。在个体或种群最优解基本交换序满足条件并操作后，如果概率ε不小于0.25，则生成随机交换子对粒子位置向量进行操作，以保持粒子群多样性、提升算法全局搜索能力。

ε=c×rand()

(10)

其中，rand()为0～1之间随机数；c∈[0,1]，为预先设定的变异操作控制参数，当该参数较大时算法收敛速度更快，较小时种群保障随机性保持较好、算法全局搜索能力更强。

2.2 迭代计算的简化

2.2.1 引入支路追加法减少中间计算量

粒子群在迭代寻优过程中更新适应函数值，只需重新计算发电机节点与需限流节点的邻接节点间的转移阻抗值。从计算原理看，转移阻抗可按照式(11)计算，中间过程仅涉及部分节点阻抗矩阵元素。

(11)

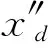
若节点i、j间装设的故障限流器满足触发条件投入限流电抗Zf，则网络阻抗矩阵元素将发生变化。为减少中间计算量，优化算法效率，本文采用支路追加法更新这部分元素值，而不必重新计算整个阻抗矩阵。可将串入的限流电抗等效为并联阻抗-zij，见式(12)。

(12)

其中，Zori为节点i、j间的线路阻抗。

在粒子群迭代寻优中，只需计算一次原阻抗矩阵所有元素值。根据不同粒子的故障限流器加装选点、选型配置，对中间计算过程使用到的元素值按式(13)进行修正即可。

(13)

2.2.2 采用降维操作缩小可行解范围

系统中可以安装故障限流器的待选点越多、故障限流器的可选类型越多时，可行组合的数量将急剧增长。为降低可行变量的组合数量，缩小算法搜索的可行解范围，避免陷入维数灾导致算法效率降低，本文采用灵敏度加权值排序的方式适当降低可行变量的维数，在确保故障限流器安装配置算法优化能力的同时优化故障限流器配置筛选策略乃至整个算法的搜索效率。

具体策略为：当安装1台固定阻抗值的故障限流器时，遍历计算所有可行安装点对应的η，并按η从大到小的顺序排列可行安装点，实际算法迭代计算中仅将前50 %的安装点纳入搜索可行范围。

2.3 RPSO-NTIS算法流程

算法流程包括如下主要步骤，具体步骤如图2所示。

a． 扫描电网中某电压等级的短路故障电流水平，设定全局限流目标，如各节点均保持一定程度的短路电流裕量θ：

θ=(Ib-If)/Ib×100 %

其中，If、Ib分别为该节点最大短路电流值、遮断电流值。

b. 确定需限流节点并计算网络阻抗矩阵值，同时设定电网中允许加装故障限流器的数量上限值Nallowed。

c. 初始故障限流器安装数量为1，随机初始化粒子群选点、选型配置序列。

d. 采用RPSO-NTIS算法进行全局寻优，得到当前数量故障限流器最优加装配置。

e. 校验当前故障限流器选点、选型最优加装配置的限流效果；根据停止条件判断，当安装故障限流器数量已达上限或限流效果已达预设目标时，算法停止并输出优化结果，否则故障限流器数量增加1，返回步骤d，直到满足算法停止条件为止。

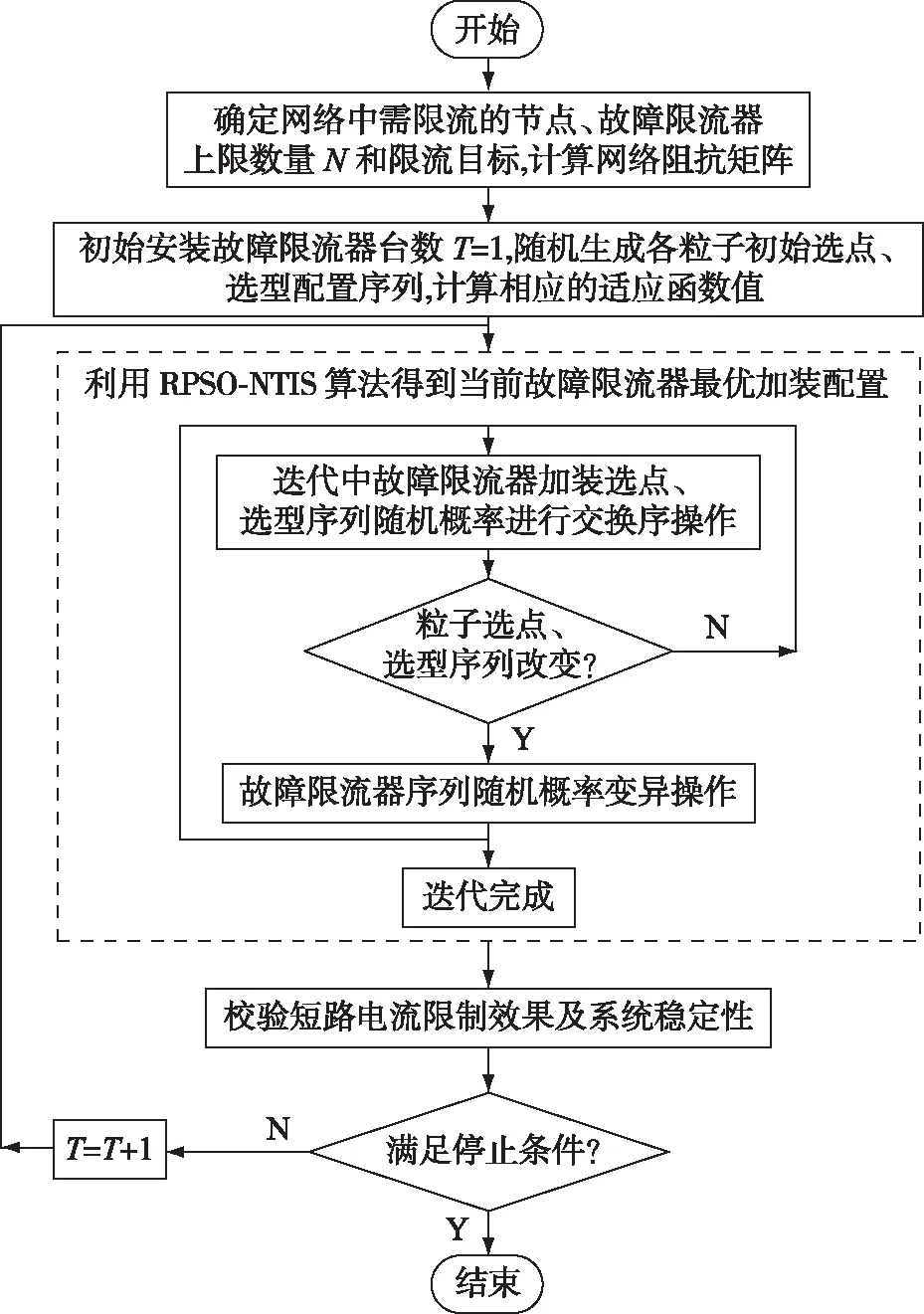
图2 RPSO-NTIS算法流程图Fig.2 Flowchart of RPSO-NTIS algorithm

3 算例测试

3.1 新英格兰39节点系统测试分析

图3 新英格兰39节点系统Fig.3 New England 39-node system

新英格兰39节点系统电力网络接线图如图3所示，该系统由46条支路、10个发电机节点、29个负荷节点构成，系统基准功率为100 MV·A，母线31为基准母线。

通过短路电流扫描可见系统中存在大量短路电流裕量θ不足20 %的节点，如表1所示。预设本次

表1 裕量不足站点Table 1 Substations with insufficient short circuit current margin

限流目标为全系统节点短路电流裕量大于20 %，故障限流器的安装数量上限为5，供选择的限流电抗为4、5、6、…、14 Ω。根据高压电抗器制造成本与电抗值之间的拟合关系曲线，本文将成本函数中的b值设置为0.991(后同)。

采用RPSO-NTIS算法进行全局寻优得到最优加装配置为方案A；按照人工经验选择靠近短路电流裕量最小节点的原则选取2组安装配置分别为方案B、C，作为对照测试方案。3种方案的对比如表2所示，可见方案B、C具备较大适应函数值，但是均小于方案A。

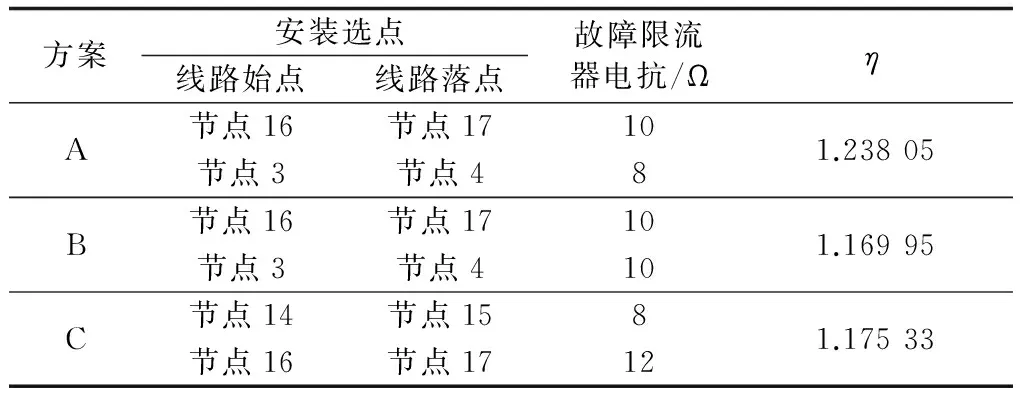
表2 3种方案结果对比Table 2 Comparison among three schemes

校验方案A及对照方案B、C的限流效果，如表3所示，表中列举了各方案下系统中θ最小的节点。

表3 3种方案的限流效果Table 3 Current-limiting effects of three schemes

由表3可见，3种方案均能达到预先设定的限流目标，方案B、C能大幅提高各节点的短路电流裕量。从经济性角度分析，方案A节省了11 %的限流电抗。鉴于限流电抗，特别是超高压限流电抗的单位造价随阻抗值上升而增大的非线性，方案A将节省更多制造成本。校验系统发生短路故障时，方案A中分别有1台和2台故障限流器触发投入限流电抗后的系统稳定性，证明方案A符合系统稳定要求，综合比较后认为方案A为最优故障限流器配置，证明了RPSO-NTIS算法的可行性和优越性。

3.2 大电网(5 969节点系统)算例测试

针对某负荷水平年南方电网5 969节点系统，以其中某省级电网为对象，计算说明本文算法的有效性。通过短路电流扫描，发现500 kV超高压系统中，所有站点短路电流均未超过遮断电流限制，但存在部分站点短路电流裕量不足10 %(如表4所示)，且地理分布零散。

表4 裕量不足站点Table 4 Substations with insufficient short circuit current margin

拟通过在若干500 kV输电线路上安装合理类型的故障限流器，使表4中各节点的短路电流裕量均提高至10 %。该省级电网可安装点位共210个。由于超高压故障限流器造价昂贵，预设允许安装的故障限流器的上限数量为5。参考世界首例在运超高压故障限流器[23]，本文设共有6种故障限流器可供选择，对应限流电抗值分别为10、12、14、16、18、20 Ω。

3.2.1 计算效率测试

随着故障限流器安装数量的增加，无论是自阻抗灵敏度辅助还是人工试凑等方法都将面临组合爆炸的困境，即使是基本PSO算法也难以确保效率。设置5组计算条件如表5所示，其中自阻抗灵敏度辅助采用遍历计算，基本PSO算法沿用带惯性系数的位移公式等，RPSO算法采用双轨解编码、交换子操作等改造。基本计算为完成一次在某种故障限流器配置方案对应的η计算，则各条件下的平均迭代次数如表5所示。为有效比较不同仿真计算效率，参照上述预设限制进行故障限流器的安装配置寻优，初始化粒子群规模均为可行解的2倍。分别统计5种不同计算条件的计算量，为排除随机性干扰对仿真结果带来的影响，统计中均采用10次仿真计算的平均值，统计结果如表5所示。

表5 优化计算统计结果Table 5 Statistical result of optimizing calculation

从寻优计算结果可见，5种计算条件均可搜索到相同的全局最优配置。但与其他计算条件算法相比，本文所提RPSO-NTIS算法的效率有明显提升。

3.2.2 限流方案效果校验和评价

使用本文RPSO-NTIS算法，进行全局优化得到最优加装配置为方案A。使用目前已有的自阻抗灵敏度排序辅助和借助工程应用经验，可以挑选短路电流最严重的节点临近区域挑选安装点及单台参数配置，得到加装配置方案B、C。作为对比组方案，同样计算其η函数值，如表6所示。由表6可见，方案B、C的η函数值均小于方案A。

分别校验这3种配置方案和未加装故障限流器下各短路电流裕度不足10 %的站点的变化情况。由表7可见：

a. 方案A、B均可使全部500 kV站点短路电流裕度达到10 %及以上，方案C虽然节省了限流电抗，却未满足限流目标；

b. 3种方案的500 kV深圳站点短路电流裕量一致，原因为深圳站点短路时仅加装于深圳—鹏城线路的故障限流器可触发，其余3台因距离较远、电流增量不满足启动条件而未触发；

表6 故障限流器加装配置方案Table 6 Schemes of FCL installation configuration

注：故障限流器均安装于双回或多回线路中短路阻抗较小的一回。

表7 各方案限流效果比较Table 7 Comparison of current limiting effect among three schemes

c. 对照方案B与推荐方案A相比，不足之处在于经济性较差，明显对某些站点限流效果过强。

为尽可能以最少限流电抗取得更均衡的限流效果，实现预设的“全网所有节点裕量均不低于10 %”的限流目标，不必过度强化对裕量已达10 %节点的限流效果。因此引入评价函数σ如式(14)所示，以评价各配置方案的全局限流效果的均衡性，σ越小说明方案的全局限流效果均衡性、经济性越好。3种方案的σ见表8。

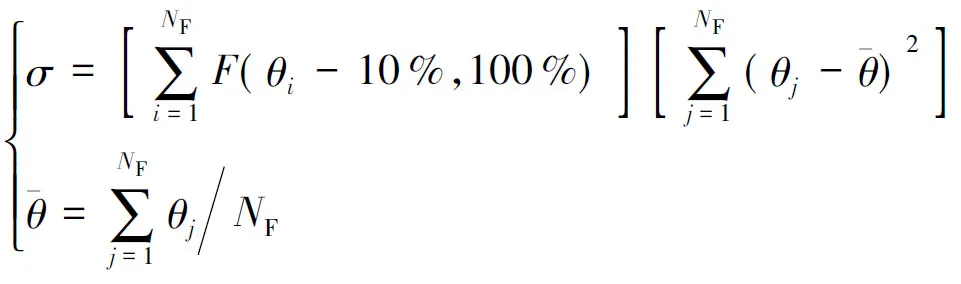
(14)

其中，F(θi-10 %,100 %)为罚函数，当θi-10 %为负数时F取值100 %，否则取值θi-10 %；θi为节点i的短路电流裕量。

由表8结果可见：

a. 未安装故障限流器时，6个短路电流裕量未达10 %的站点均受罚函数影响，放大了对评价函数的贡献值，因此σ函数值非常大；

表8 各方案评价函数σ的比较Table 8 Comparison of σ amomg schemes

b. 方案B对部分站点限流作用较强，虽然达成预设限流目标，但限流效果均衡性不及推荐方案A；

c. 方案C为节省限流电抗，仍然存在裕量不足10 %的站点，说明未达成预设限流目标，σ函数值也较大；

d. 综合考虑限流效果和限流成本后，方案A满足限流目标且经济性更强，为本文推荐方案。

最后，校验各种情况下的系统稳定性，包括扫面全网主要线路、母线故障期间最低节点电压，以及电源间最大相角差的前2位，结果见表9，表中最低电压为标幺值。由表9可见，推荐方案A不会破坏系统稳定，因此认为其为当前限流目标下最优配置方案，证实了RPSO-NTIS算法的有效性和优越性。

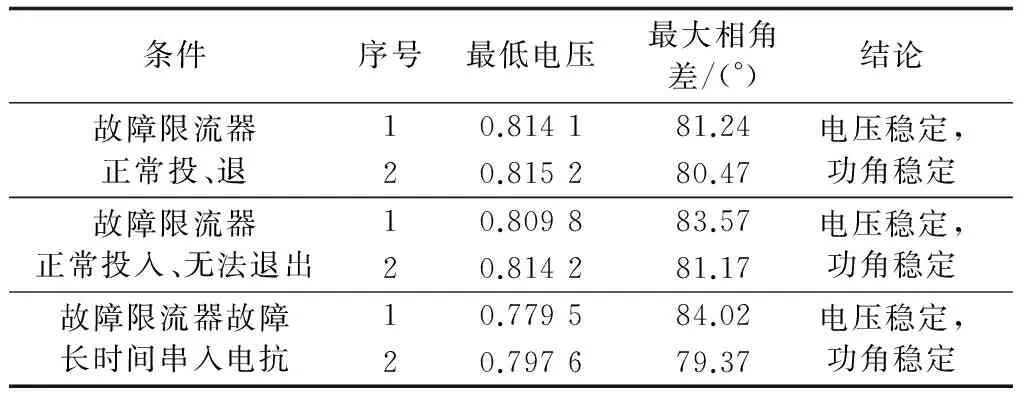
表9 推荐方案校验结果Table 9 Verification results of Scheme A

4 结论

a. 作为当前限流问题研究的热点，故障限流器能有效缓解短路电流限流与确保供电可靠性之间的矛盾。随着世界首台超高压故障限流器在我国华东电网成功投运，其应用前景将越发广阔。针对故障限流器加装配置问题，本文提出了一种RPSO-NTIS算法，能快速有效搜索故障限流器加装选点、选型等配置的全局最优方案，避免了传统人工选择、自阻抗灵敏度辅助灯方法存在的随意性和局限性。同时，该算法便于编程实现，适用于不同规模、不同电压等级的电网系统，具有良好的拓展性和灵活的应用性。

b. 提出一种基于NTIS的加权适应函数作为全局限流效果衡量指标。与传统的基于自阻抗的限流效果衡量指标相比，该指标可针对电网中电源集中分布情况，区分短路电流关键路径、反映限流经济代价、指示全局限流效果及均衡水平，以获得更好的全局限流效果和均衡性。

c. 通过新英格兰39节点系统和南方电网某省级电网系统计算分析，验证了本文RPSO-NTIS算法的有效性。

参考文献：

[ 1 ] 李基康，滕欢，郭宁. 采用相对熵组合赋权法的500 kV电网短路电流抑制策略优化决策[J]. 电网技术，2016，40(6)：1811-1817.

LI Jikang，TENG Huan，GUO Ning. An optimal decision to restrain short circuit current for 500 kV power grids with combinatorial weighting method of relative entropy[J]. Power System Technology，2016，40(6)：1811-1817.

[ 2 ] 黄根，罗滇生，李帅虎，等. 基于综合灵敏度分析限流的最优断线措施[J]. 电网技术，2016，40(1)：309-315.

HUANG Gen，LUO Diansheng，LI Shuaihu，et al. Optimal line-outage measure based on comprehensive sensitivity analysis to limit short-circuit current[J]. Power System Technology，2016，40(1)：309-315.

[ 3 ] 廖国栋，谢欣涛，侯益灵，等. 特高压接入湖南电网后 500 kV 母线三相短路电流超标问题分析[J]. 高电压技术，2015，41(3)：747-753.

LIAO Guodong，XIE Xintao，HOU Yiling，et al. Analysis on the problems of three-phase short-circuit current over-limited of 500 kV bus when UHV connected to Hunan Power Grid[J]. High Voltage Engineering，2015，41(3)：747-753.

[ 4 ] 翁华，徐政. 一种考虑短路电流指标的动态等值方法[J]. 电力自动化设备，2012，32(9)：85-100.

WENG Hua，XU Zheng. Dynamic equivalence based on short circuit current index[J]. Electric Power Automation Equipment，2012，32(9)：85-100.

[ 5 ] 唐宗华. 面向高压电网的经济性故障限流器的关键技术研究[D]. 济南：山东大学，2013.

TANG Zonghua. Study of key technology of economical-type fault current limiter on HV Grid[D]. Ji’nan：Shandong University，2013.

[ 6 ] 张玉红，张彦涛，李付强，等.故障电流限制器参数选择的解析法研究[J].电工电能新技术，2016，35(2):31-37．

ZHANG Yuhong，ZHANG Yantao，LI Fuqiang，et al. Analytical method to select fault current limiter parameter[J]. Advanced Technology of Electrical Engineering and Energy，2016，35(2):31-37.

[ 7 ] 应林志，王建全，陈迅，等. 广东电网超高压短路限流器优化配置方案[J]. 电力系统自动化，2012，36(4)：96-100.

YING Linzhi，WANG Jianquan，CHEN Xun，et al. An optimal confi-guration scheme for ultra-high voltage short-circuit current limiter in Guangdong Power Grid[J]. Automation of Electric Power Systems，2012，36(4)：96-100.

[ 8 ] PRASERT C，KOMSAN H. PSO based approach for optimum fault current limiter placement in power system[C]∥2012 International Conference on Electrical Engineering/Electronics，Computer，Telecommunications and Information Technology(ECTI-CON). Phet-chaburi，Thailand：IEEE，2012：1-4.

[ 9 ] 胡文旺，卫志农，孙国强，等. 基于灵敏度法的超导故障限流器的优化配置[J]. 电力系统自动化，2012，36(22)：62-67.

HU Wenwang，WEI Zhinong，SUN Guoqiang，et al. Optimal allocation of superconducting fault current limiters based on sensitivity method[J]. Automation of Electric Power Systems，2012，36(22)：62-67.

[10] 肖怀硕，李清泉，张岩，等. 基于非支配排序遗传改进算法的故障限流器的优化配置[J]. 电网技术，2016，40(8)：2443-2449.

XIAO Huaishuo，LI Qingquan，ZHANG Yan，et al. Optimization of fault current limiter configuration based on improved NSGA-2[J]. Power System Technology，2016，40(8)：2443-2449.

[11] 陈柏超，魏亮亮，雷洋，等. 基于免疫算法的高温超导故障限流器Pareto多目标优化配置[J]. 电网技术，2015，39(5)：1343-1350．

CHEN Baichao，WEI Liangliang，LEI Yang，et al． Immune algorithm based Pareto multi-objective optimal allocation of high temperature superconductor-fault current limiters[J]． Power System Technology，2015，39(5)：1343-1350．

[12] 李光琦. 电力系统暂态分析[M]. 北京：中国电力出版社，2007：63-65.

[13] 王锡凡，方万良，杜正春. 现代电力系统分析[M]. 北京：科学出版社，2003：10-13.

[14] RAMADAN H S，BENDARY A F，NAGY S. Particle swarm optimization algorithm for capacitor allocation problem in distribution systems with wind turbine generators[J]. International Journal of Electrical Power and Energy Systems，2017，84：143-152.

[15] MEHDINEJAD M，MOHAMMADI-IVATLOO B，DADASHZADEH-BONAB R. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms[J]. International Journal of Electrical Power and Energy Systems，2016，83(142-0615)：104-116.

[16] 刘先正，温家良，潘艳，等. 采用改进粒子群算法的直流电网最

优潮流控制[J]. 电网技术，2017，41(3)：715-720.

LIU Xianzheng，WEN Jialiang，PAN Yan，et al. OPF control of DC-grid using improved PSO algorithm[J]. Power System Technology，2017，41(3)：715-720.

[17] 周任军，晁岱旭，李新军，等. 空间耦合粒子群优化算法及峰谷电价下IES-CCHP区域联合调度[J]. 电力自动化设备，2016，36(12)：11-17.

ZHOU Renjun，CHAO Daixu，LI Xinjun，et al. SC-PSO algorithm and IES-CCHP regional joint dispatch with TOU price[J]. Electric Power Automation Equipment，2016，36(12)：11-17.

[18] ZIELINSKI K，WEITKEMPER P，LAUR R，et al. Optimization of power allocation for interference cancellation with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation，2009，13(1)：128-150.

[19] 蒋跃强，鲍伟，吴建坤. 超高压电网故障电流限制器在电网中的应用评价[J]. 华东电力，2011，39(1)：49-51.

JIANG Yueqiang，BAO Wei，WU Jiankun. Application evaluation on the EHV fault current limiter in power grid[J]. East China Electric Power，2011，39(1)：49-51.