特高压分布电容对电流差动保护的影响分析及对策
2018-05-18宋璇坤申洪明黄少锋肖智宏
宋璇坤 ,申洪明 ,,黄少锋 ,韩 柳 ,肖智宏
(1.国网经济技术研究院有限公司,北京 102209;2.华北电力大学 新能源电力系统国家重点实验室,北京 102206)
0 引言
全球能源互联网主要由特高压技术、清洁能源、智能电网三部分组成[1],其中特高压电网是能源互联网的传输通道,因此受到了广泛关注。特高压技术虽然在实现远距离、大容量输电方面具有较大优势,但是也给电力系统的安全稳定运行带来了一定影响。
继电保护作为电力系统的第一道防线,对维持系统的安全稳定运行具有重要作用。在特高压输电网中,保护一旦误动,有可能造成大规模停电事故,造成不必要的经济损失。
特高压长线路中过大的分布电容有可能造成区外故障、区外故障切除或者线路空载时差动保护误动[2-4];为了提高特高压输电线路的传输能力,往往在线路中接入大串补度的电容,但大串补度电容可能引起内部故障时差动保护灵敏度不足导致拒动的发生[5-7];为了补偿过大的电容电流,可以采用并联电抗器方法。现阶段,采用并联电抗器补偿电容电流的方法已取得了较好的效果,但当线路采用并联可控高抗时,由于电抗器输出电流不断调整,从而影响了电流差动保护的正确动作,可能造成保护误动[8]。为此,本文将重点围绕特高压分布电容对电流差动保护的影响展开分析。
本文在介绍传统解决措施的基础上,提出了一种基于动作电流相角信息的解决措施。分析表明,线路内部发生单相接地故障时,动作电流的相角较于正常运行和外部故障时会顺时针转过一定的角度;而发生相间故障时,不同故障相的动作电流相角虽然转动方向不一致,但也会转过较大的角度。进而将相角信息与传统的动作逻辑相配合,可以很好地解决特高压分布电容对电流差动保护的影响。
本文介绍了分布电容对电流差动保护影响的机理;阐述了利用动作电流相角信息解决分布电容引起电流差动保护误动的措施,并给出了新的综合电流差动保护动作逻辑;基于PSCAD/EMTDC搭建仿真模型,仿真结果验证了所提方法的有效性。
1 分布电容对电流差动保护的影响机理
图1给出了典型的双电源系统图,图中线路采用π型等值模型。图中,C为分布电容;iM、iN分别为线路M、N两侧保护安装处流过的电流;iC为流过电容的电流;iF为流过故障点的故障电流;Rg为过渡电阻。
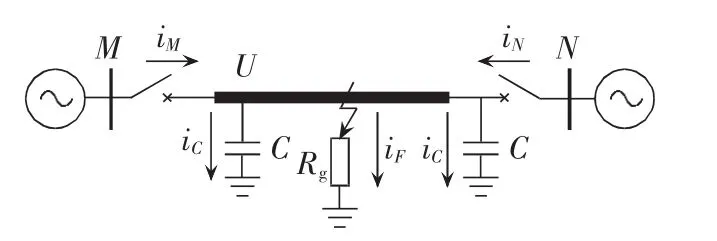
图1 典型的双电源系统图Fig.1 Schematic diagram of typical system with dual power sources
基于全电流的电流差动保护的动作判据为:
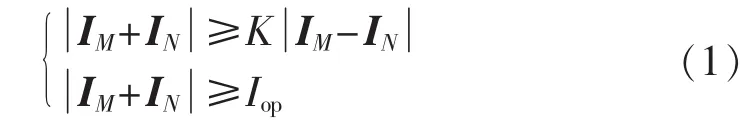
其中,IM、IN为 iM、iN的相量形式;K 为制动系数,一般取为0.5;Iop为动作门槛值。通过式(1)可以看出,电流差动保护判据虽然仅对动作电流和制动电流的幅值进行了比较,但动作电流和制动电流同时也包含了相角信息。
在一般电压等级的电网中,分布电容C较小,容抗1/(ωC)较大,导致电容电流iC较小。因此当系统正常运行时,动作量(全线路电容电流)幅值较小,保护能可靠不动作。但在特高压电网中,分布电容C很大,导致了容抗1/(ωC)很小,所以电容电流iC较大,此时动作量幅值增大,特高压长线路在发生区外故障、区外故障切除或者线路空载时很可能超过保护动作门槛值,进而导致保护误动。图2给出了在不同分布电容下动作电流(全线电容电流)的幅值曲线,通过图2可以看出,随着分布电容C的增大,动作电流的幅值也显著增大。
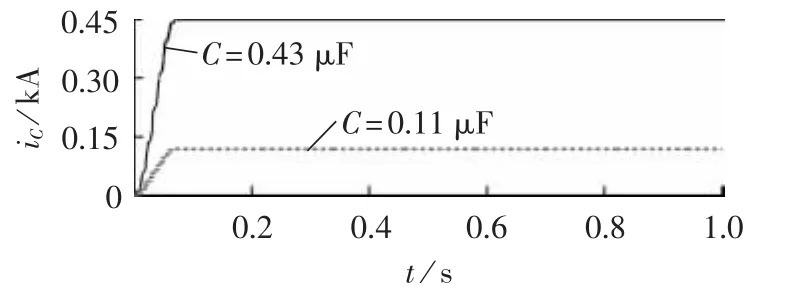
图2 不同分布电容下的电容电流曲线Fig.2 Curve of capacitance current under different capacitances
解决特高压分布电容引起的电流差动保护误动的措施一般分为3类:
a.提高动作门槛值或制动系数,但会降低发生内部故障时保护的灵敏度;
b.通过计算补偿分布电容引起的电流[9],这是目前工程中较为常用的方法之一,但需要逐级计算线路电容电流的大小,进而进行补偿,计算过程较为繁琐;
c.采用不受分布电容影响的新纵联保护原理[10-11],该措施采用了完全不同于传统电流差动保护的原理,因此在工程方面的应用受到了限制。
下文给出一种基于动作电流相角信息的解决特高压分布电容对差动保护影响的措施。
2 基于动作电流相角信息的解决措施
2.1 发生单相接地故障时动作电流相角特征
发生线路内部故障时,记流过故障点的电流的相量形式为IF。由于横向故障中,单相接地故障的概率最高,下文先以单相接地故障为例分析各电流相角特征,其序网图如图3所示。
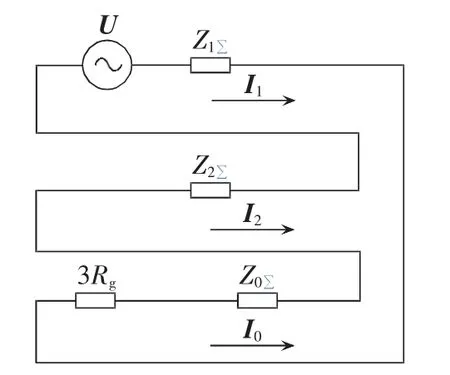
图3 单相接地故障序网图Fig.3 Sequence diagram of single-phase grounding fault
由图1可以得出电容电流为:

由图3可知:
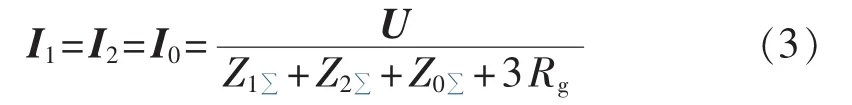
其中,I1、I2、I0分别为故障点处的正、负、零序电流;U为故障点未发生故障时的电压;Z1∑、Z2∑、Z0∑分别为正序、负序、零序综合电阻。
流过故障点处的电流为:

由式(2)—(4)可以得到图4,图4以电压U的相位为参考相位,图中IC、IF分别为iC、iF的相量形式。由图4可以看出,由于短路电流iF呈现感性性质(滞后于参考电压),所以动作电流iC+iF的相角相较于电流iC而言,顺时针转过角度ΔP;随着过渡电阻的增大,U的幅值也随之变大,造成了电容电流iC变大,同时由式(3)可知,电流iF滞后电压的角度φ变小,如图4中 φ 与 φ′所示。此时动作电流 i′C+i′F相较于电容电流 i′C顺时针转过了角度 ΔP′。显然 ΔP′<ΔP。但当线路正常运行或者发生外部故障时,由于动作电流并不反映短路电流iF,只反映了电容电流iC,因此电容电流i′C的相角变化不大。
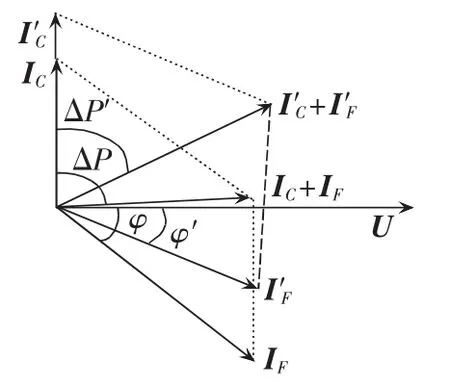
图4 单相接地故障时的相量图Fig.4 Phasor diagram of single-phase grounding fault
通过上文的分析可以得出发生单相接地故障时动作电流的相角特征如下。
a.线路正常运行或者发生外部故障时,动作电流只反映电容电流,因此其动作电流的相角变化不大。
b.线路发生内部故障时,动作电流包含了电容电流和短路电流,此时动作电流的相角较于正常运行和发生外部故障时要顺时针转过一定的角度。同时由于特高压线路短路时的短路电流一般要远大于电容电流,因此动作电流iC+iF顺时针转过的角度绝对值较大。
2.2 发生相间故障时的动作电流相角特征
图5给出了BC相在F点发生相间故障时的简单示意图。由于发生相间故障时弧光电阻较小,因此可以不考虑过渡电阻。
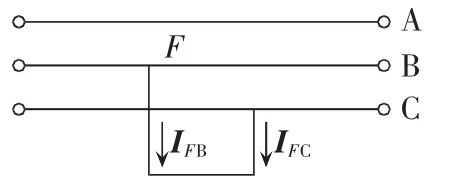
图5 相间故障示意图Fig.5 Schematic diagram of phase-to-phase fault
线路发生相间故障时,其序网图在短路点处并联连接,且不存在零序支路,其正、负序电流表达式为:
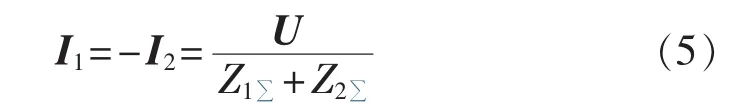
由(5)可得 IFB、IFC的表达式为:

由式(5)、(6)可得出发生相间故障时动作电流相量图,如图6所示,图6 中 IA(C)、IB(C)、IC(C)分别为A、B、C相的电容电流。由图6可以看出,在发生相间故障时,不同故障相的动作电流转动方向不一致:超前相(B 相)动作电流 IB(C)+IFB较正常动作电流 IB(C)逆时针转过 ΔPB角度,滞后相(C 相)动作电流 IC(C)+IFC较正常动作电流 IC(C)转过ΔPC角度,但旋转的方向取决于IFC的初始位置。
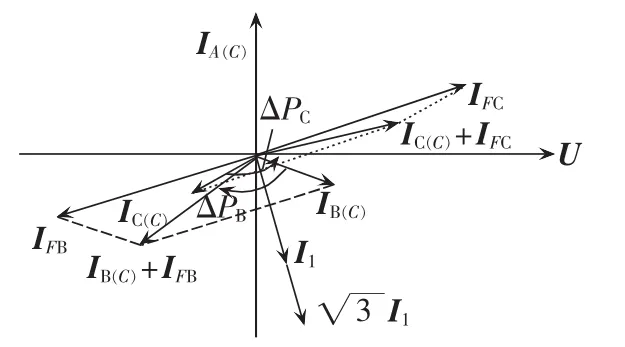
图6 相间故障相量图Fig.6 Phasor diagram of phase-to-phase fault
2.3 发生对称性故障时的动作电流相角特征
当线路发生对称性故障时,由于三相仍然对称,不需要采用序分量法对短路电流进行计算,只需按单相进行计算。图7给出了在此类故障下动作电流IC+IF的相量图。通过图7可以看出,此时动作电流较正常动作电流iC顺时针转过角度ΔP。
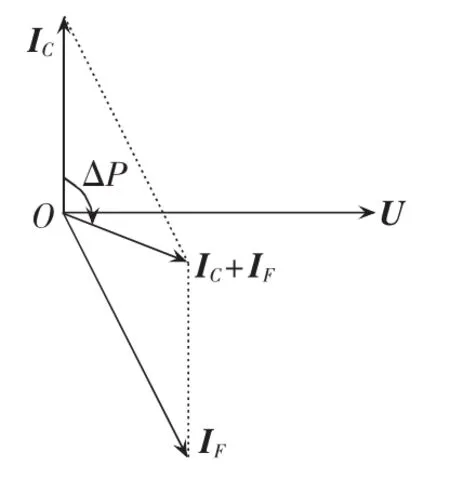
图7 对称性故障相量图Fig.7 Schematic diagram of symmetrical fault
其他故障形式分析过程与此类似,在此不再赘述,只给出一般性结论:当线路发生BC两相内部接地故障时,无论是超前相还是滞后相,动作电流都转过很大角度:一般地,超前相的相角逆时针转动,而滞后相的相角顺时针转动。
通过上文的分析可以看出,无论是接地故障还是相间故障,总存在故障相的动作电流在发生内部故障时会转过较大角度,而正常运行或者发生外部故障时,三相动作电流的相角几乎不发生改变。因此可以通过动作电流是否转过较大的角度值来决定电流差动保护是否动作,其动作流程图如图8所示。
图8中,ΔP为动作电流IM+IN相角的变化值;δ为设置的转过角度门槛值。考虑需要躲过线路外部故障产生的不平衡角度值以及测量装置等造成的误差,可以取 δ=50°。
3 仿真验证
基于PSCAD/EMTDC搭建了如图1所示的仿真模型,其中交流侧电压为1 000 kV,线路长度为500 km,线路参数如表1所示,表中 R1、X1、XC1分别为正序电阻、电抗、容抗,R0、X0、XC0分别为零序电阻、电抗、容抗。以A相接地故障为例,故障时刻为0.5s。
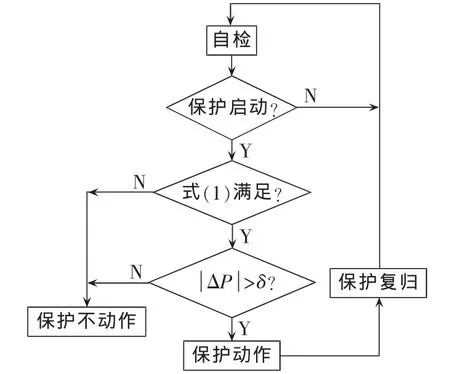
图8 本文所提动作逻辑的流程图Fig.8 Flowchart of proposed logic
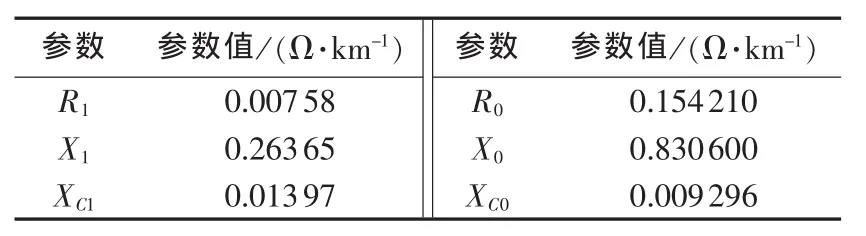
表1 1000 kV线路参数Table 1 Parameters of 1000 kV power transmission line
3.1 单相内部接地故障仿真分析
图9给出了线路发生单相内部金属性接地故障时动作电流相角的变化曲线以及相量图,图中,P、P′分别为故障前、后的相角。通过图9(a)可以看出,此时动作电流相角由正常运行时的3°变为-160°,在坐标平面内,相当于动作电流从第Ⅰ象限顺时针转到了第Ⅲ象限,转过的角度为-163°。根据图8的动作逻辑可以看出,电流差动保护能正确动作。
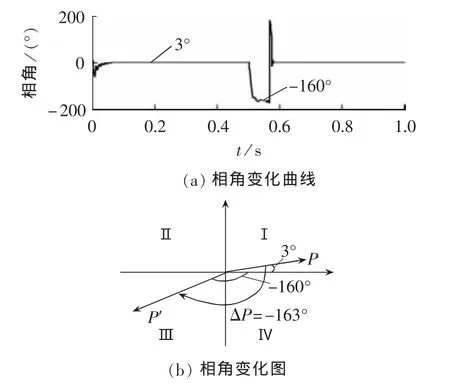
图9 内部故障时的仿真结果Fig.9 Simulative results under internal fault
3.2 外部故障仿真分析
图10给出了发生外部故障时动作电流相角变化曲线,通过图10可以看出,此时相角变化非常有限,几乎不变,与内部故障时差异很大。
3.3 两相接地故障仿真分析
图11给出了发生BC相经过10 Ω过渡电阻接地故障时故障相动作电流相角变化情况,其中PB为B相动作电流相角,PC为C相动作电流相角。通过图11可以看出,超前相B相动作电流逆时针转过126°,而滞后相C相动作电流顺时针转过150°,其转过的角度值远大于整定值50°,保护能可靠动作。
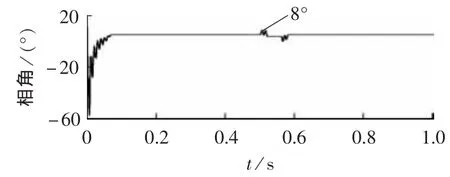
图10 外部故障时的仿真结果Fig.10 Simulative results under external fault
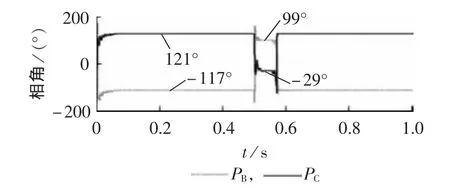
图11 两相接地故障时的仿真结果Fig.11 Simulative results under dual-phase grounding fault
表2给出了不同故障类型下动作电流相角的变化结果。表中,i表示内部故障,o表示外部故障,FiA(0)表示A相发生内部接地故障,过渡电阻为0;FoA(10)表示发生线路外部故障,过渡电阻为 10 Ω;FiBCG(15)表示BC两相经15 Ω过渡电阻发生内部接地故障,第2列其他参数含义类推;X/Y形式的数据中,X对应B相数值,Y对应C相数值。

表2 不同故障形式下的仿真结果Table 2 Simulative results under different faults
由表2可以看出,发生内部故障时动作电流转过较大角度,并且对同一故障形式而言,随着过渡电阻的增大,转过的角度越小,如表2中编号1—3的数据所示;而发生外部故障时转过的角度很小,几乎不变,如表中编号5、6的数据所示。因此本文所提的电流差动保护逻辑可以很好地解决分布电容带来的问题。
4 结论
特高压电网分布电容会对电流差动保护产生影响,本文利用动作电流相角的变化特征与传统的保护判据构成动作逻辑。本文动作逻辑需要同时满足2个动作条件:动作电流相角转过一定角度值,同时动作电流大于整定值。本文保护判据只需增加动作电流的相角信息,并不需要添加其他硬件或者接线,因此具有一定的工程应用价值。
参考文献:
[1]田世明,栾文鹏,张东霞,等.能源互联网技术形态与关键技术[J].中国电机工程学报,2015,35(14):3482-3494.TIAN Shiming,LUAN Wenpeng,ZHANG Dongxia,et al.Technical forms and key technologies on energy internet[J].Proceedings of the CSEE,2015,35(14):3482-3494.
[2]邓翔天,袁荣湘,肖振锋,等.基于瞬时功率理论的输电线路分相电流差动保护[J].电力自动化设备,2014,34(11):82-89.DENG Xiangtian,YUAN Rongxiang,XIAO Zhenfeng,et al.Splitphase differentialcurrentprotection based on instantaneous power theory for power transmission line[J].Electric Power Automation Equipment,2014,34(11):82-89.
[3]王增平,姜宪国,张执超,等.智能电网环境下的继电保护[J].电力系统保护与控制,2013,41(2):19-24.WANG Zengping,JIANG Xianguo,ZHANG Zhichao,et al.Relay protection for smart grid[J].Power System Protection and Control,2013,41(2):19-24.
[4]张尧.1000 kV特高压输电线路分布电容对继电保护影响的研究[D].南宁:广西大学,2014.ZHANG Yao.Impact study of 1 000 kV UHV AC transmission line distributed capacitance on protective relay performance[D].Nanning:Guangxi University,2014.
[5]高超,郑涛,毕天姝,等.特高压多串补系统电流特性分析[J].电工技术学报,2015,30(20):193-198.GAO Chao,ZHENG Tao,BI Tianshu,et al.Analysis on current characteristics of ultra high transmission line with multi series compensation capacitors[J].Transactions of China Electrotechnical Society,2015,30(20):193-198.
[6]唐萃,尹项根,戚宣威,等.大串补度输电线路的电流差动保护分析与对策[J].电力系统自动化,2015,39(7):157-163.TANG Cui,YIN Xianggen,QIXuanwei,etal.Analysis and countermeasures of current differential protection on transmission line with high series compensation degree[J].Automation of Electric Power Systems,2015,39(7):157-163.
[7]李猛.超高压750 kV输电系统继电保护应用技术研究[D].北京:华北电力大学,2015.LI Meng.Study on application technology of extra high voltage 750 kV transmission system relay protection [D].Beijing:North China Electric Power University,2015.
[8]张健康,粟小华,胡勇,等.大容量可控电抗器对线路差动保护的影响及解决措施[J].电力系统自动化,2014,38(1):115-120.ZHANG Jiankang,SU Xiaohua,HU Yong,et al.Impact of largecapacity controllable shunt reactor on line differential current protection and solutions[J].Automation of Electric Power Systems,2014,38(1):115-120.
[9]黄少锋.电力系统继电保护原理[M].北京:中国电力出版社,2015:159-160.
[10]申全宇,宋国兵,马超.适用于带并联电抗器输电线路的电流模
(continued on page 192)(continued from page 172)型识别纵联保护新原理[J].电力自动化设备,2014,34(1):109-114.SHEN Quanyu,SONG Guobing,MA Chao.Pilot protection principle based on current model recognition applicable to transmission line with shunt reactors[J].Electric Power Automation Equipment,2014,34(1):109-114.
[11]马静,裴讯,马伟,等.基于故障分量虚拟阻抗的线路差动保护原理[J].电力自动化设备,2014,34(12):58-65.MA Jing,PEI Xun,MA Wei,et al.Quick tracking of limitinduced bifurcation point of voltage stability[J].Electric Power Automation Equipment,2014,34(12):58-65.
