B E MD全矢包络谱及其在T R T故障诊断中的应用

黄传金 ，宋海军 ，秦 娜

（1.郑州工程技术学院 机电与车辆工程学院，河南 郑州 450044；2.浙江大学 机械工程学院，浙江 杭州 310007；3.西南交通大学 电气工程学院，四川 成都 610031）

0 引言

为提高大型旋转机械运行的可靠性，高炉煤气余压透平发电装置TRT（blast furnace Top gas Recovery Turbine unit）等常采用监测设备获取机械运行状态信息［1-3］。在此基础上，进行准确的信号处理与故障特征提取，进而识别故障类型，为大型机械的健康运行提供技术支撑［4］。运用一些先进的数字信号处理方法，如小波变换［5-6］、固有时间尺度分解［7］、经验模态分解（EMD）以及集成经验模态分解［8-9］、局部均值分解［10］和子空间［11］等方法可提取故障信号特征。

不同方向的振动信号可能表征不同的特征信息，上述方法根据单源信息识别故障易产生漏判和误判［12-13］。为提高诊断可靠性，基于同源信息融合的诊断方法被提出，其中采用全矢谱获取的故障特征更加全面［13］。针对振动信号的非线性，基于小波、经验模态分解和局部均值分解的全矢谱被提出［14-16］。全矢谱分析的是一个复信号（由互相垂直方向上的振动信号组成），而目前的常用方法是运用一元信号处理方法（如经验模态分解、局部均值分解）分别分析单个方向上的信号，并将分析结果按一一对应的原则组成相应的复数，然后运用全矢谱进行数据融合，得到更全面的故障信号特征。由于不同方向上的信号存在差异，由此可能造成分解后的信号数量不同，给数据融合带来困难。上述问题产生的原因主要是分析对象是二元信号，而采用的方法却依然是一元信号分析方法。

2007年Rilling.G等人将经验模态分解扩展到二元空间，提出了二元经验模态分解BEMD（Bivariate Empirical Mode Decomposition）［17］。BEMD 认为二元信号为快速旋转信号和慢速旋转信号的叠加，其可将旋转速度不同的信号分离［17］。BEMD已用于海洋水下浮标数据分析［17］、光电信号检测［18］，而 在TRT等机械振动故障领域的研究还未见报道。

转子同一截面互相垂直方向的信号可组成旋转速度不同的二元信号，根据这一特点，本文从信息融合角度考虑，运用正交采样技术获取转子同一截面互相垂直方向上的振动信号，并将其组成一个复数信号；然后运用BEMD对该复数信号进行自适应分解，获取复数形式的固有模态分量CIMFs（Complex Intrinsic Mode Functions），再运用希尔伯特变换HT（Hilbert Transform）对CIMFs进行解调，得到复包络信号；最后，运用全矢谱（全矢谱技术的理论与算法可参考文献［13-14］）融合复包络信号，获取复包络信号的全矢包络谱，进而判断故障类型。转子碰摩信号以及TRT的故障信号分析结果证明了所提方法的可行性和有效性。

1 BEMD及其改进

1.1 BEMD原理

BEMD认为二元信号为快速旋转信号和慢速旋转信号的叠加，该方法将二元信号投影到不同方向并求其不同方向投影的极值点，运用插值函数拟合各个方向的包络信号，然后求其平均值获取局部均值，将局部均值函数从原始信号中分离，若剩余信号仍为复合旋转信号，则对剩余信号重复以上过程，直到待分解信号中没有旋转信号为止。

在BEMD的具体实现中，Rilling.G等人提出的BEMD有3种具体形式，其中，当投影方向为偶数时，第2种形式可简化为用一维的经验模态分解筛选操作表示。本文主要介绍了第2种方法，其他方法请参见文献［17］。

对于复数信号 z（t），其 BEMD 过程如下［17-18］。

a.将每个复数信号投影到N个方向，并将同一时刻t内同一方向所有复数信号的投影值相加，形成N个随时间变化的信号，第k个方向的投影值可用式（1）表示。

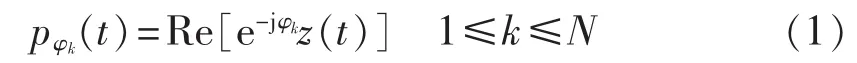
其中，φk=2πk /N。

b.提取信号 pφk（t）的最大值。

c.对集合进行插值获取φk方向上的切线 e′φk（t）。

d.计算所有切线的均值：

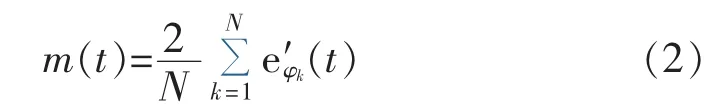
e.从原始信号中减去均值信号获得：

f.重复上述过程并求解：

当 SD在 0.2～0.3范围内时，停止本次迭代过程，分解获得第1个旋转分量，记为c1（t），则有：

g.从原始信号中把第1个旋转分量分解出来，获得新的待分解信号 r1（t）=z（t）-c1（t），若 r1（t）仍为旋转复合信号，则对r1（t）重复以上步骤，获得其他的旋转信号。当从待分解信号中分解不出新的旋转信号时，上述筛分过程结束，待处理信号被分解为一系列旋转信号的叠加，且每个旋转信号均为复数信号。

经过BEMD过程后，复数信号z（t）可用下式表示：

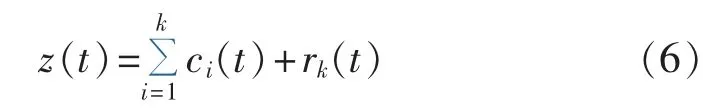
其中，ci（t）为复旋转分量；rk（t）为残余信号。

值得注意的是，BEMD的结束条件容易产生较多的旋转分量，影响BEMD的速度。考虑到振动故障对应的旋转模态是有限的，本文提出了基于能量阀值的BEMD结束条件，即设定一个比例阀值，待分解信号与原始信号的能量之比小于某个数值，即满足式（7）时，BEMD 结束。

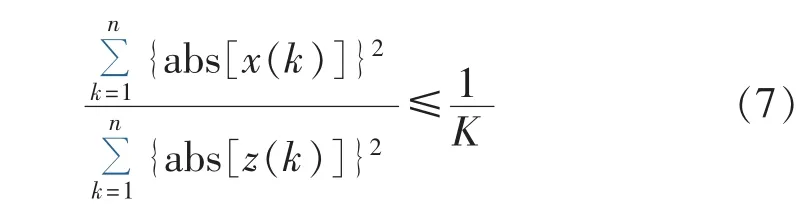
其中，n为数据长度；x为待分解信号；abs表示求模运算；K的取值范围在10～15之间，即剩余信号的能量低于原始信号能量的10%时，BEMD结束。

1.2 对旋转机械振动信号进行BEMD可行性验证

对旋转信号进行BEMD时，要求旋转信号围绕0点附近旋转，而旋转机械振动信号满足这一条件。为简单起见，本文选择典型的Jeffcott刚性转子，即轴承系统动力学方程，运用龙格-库塔法对其求解，然后将水平和垂直方向的数据组成复数信号，以验证对旋转机械振动信号进行BEMD的可行性。

圆盘中心处水平和垂直方向的位移和速度组成的旋转信号如图1所示，从图1可知，圆盘中心处的位移信号和速度信号在三维空间中是旋转信号，且位移信号和速度信号的运动轨迹区别较大。

图1 圆盘中心处的位移和速度信号Fig.1 Displacement and velocity signal of platform center

图2 位移信号的BEMD结果Fig.2 BEMD results of displacement signal

图3 速度信号的BEMD结果Fig.3 BEMD results of speed signal

将式（7）作为分解终止条件（K=10）分别对图1（b）、（d）中的旋转信号进行 BEMD，则位移信号和速度信号的旋转分量分别如图2和图3所示。图2中，残差信号和原始信号的能量比为0.000 876 14，c2和残差的能量和与原始信号的能量比为0.9398。图3中，残差信号和原始信号的能量比为0.0029，c2和残差的能量和与原始信号的能量比为0.7274。从图2和图3可知，由BEMD得到的旋转分量数量与机械旋转信号原有的旋转模态数量相符，这样更有利于提取完整的故障特征。从图2和图3中c1和c2的平面图可知，运用BEMD还可提纯转子轴心轨迹。

碰摩等故障引起的故障信号为调制信号，通过解调可清晰地提取调制信号的特征。为此，本文在BEMD的基础上提出全矢包络解调方法。

2 旋转信号的包络解调方法和全矢包络谱

2.1 基于HT的二元旋转信号的包络解调方法

对于单通道信号，运用希尔伯特解调可获取包络信号。本文根据正交采样获取的数据信号特点，提出了一种基于HT的二元旋转信号解调方法。假设互相垂直方向上获取的时序信号分别为x（t）和y（t），令 z（t）=x（t）+jy（t），则有：

基于HT的二元旋转信号解调步骤如下。

a.令 k=1，对 Re［e-jkπ/2z（t）］进行 HT，z（t）的虚部信号 y（t）的 HT 结果为（t），即：

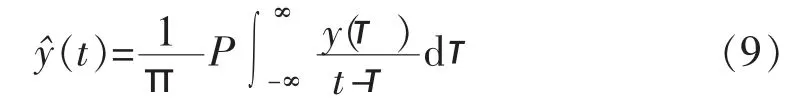
b.将 y（t）和（t）构成解析信号 zy（t），即：

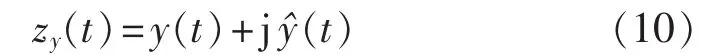
c.根据解析信号 zy（t）获取 z（t）虚部信号的包络信号，即：

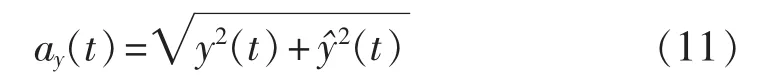
d.令k=2，重复以上步骤可得z（t）实部信号的包络信号，即：

其中，（t）为 x（t）的 HT 结果。

2.2 基于BEMD和HT的全矢包络谱方法

基于BEMD和HT的全矢包络谱方法如下。

a.通过正交采样技术得振动信号z（t）=x+jy，其中x和y为同一截面上互相垂直的2个传感器采集的振动信号。

b.运用BEMD对上述信号进行分解，则根据式（6）可获取复旋转分量ci（t）。不妨假设复旋转分量ci（t）=cxi（t）+jcyi（t）。

c.根据2.1节中的基于HT的二元旋转信号的包络解调方法，分别解调出 cxi（t）和cyi（t）的包络信号axi（t）和ayi（t）。

d.令复包络信号 ai（t）=axi（t）+jayi（t），然后对复包络信号进行复数傅里叶变换。

e.用全矢谱对复数傅里叶变换结果进行信息融合，以主振矢评价振动强度，作为相应包络信号的全矢谱，称其为第i阶全矢包络谱。

3 算例分析

3.1 碰摩故障

在柔性转子试验台上设置碰摩故障（转速为40 r/s）；采用正交采样技术分别获取水平方向和垂直方向的振动信号x、y（采样频率为2048 Hz，采样时长为0.5 s）；令z=x+jy，则z的实部信号、虚部信号的时域波形图、z的二维平面图及相应的频谱如图4所示，图中 X=50 Hz，表示基频。从图4（a）、（b）可知，Re［z］、Im［z］有明显的冲击，并且规律性比较强（每隔固定时间有一个冲击），而且Re［z］的幅值较大；图4（c）、（d）显示轴心轨迹比较凌乱，轴心的运动轨迹不再是一个椭圆，由此可知发生了振动故障；由图4（e）、（f）可知，z的实部和虚部信号在 2 个固有频率（542Hz和862Hz）处都有调制现象，而且调制边频带是非对称的，由此可知振动信号中存在调幅信号，且 Re［z］幅值较大。

对复数信号z进行BEMD得到的系列旋转分量c的三维图和平面图分别如图5、图6所示（K=10）。从图5、图6 可知，c1、c2、c3的运动轨迹比较凌乱，这些旋转分量含有故障特征信息，而c4的运动轨迹为不规则的椭圆。为全面考察旋转分量，在频域内对其进行分析，旋转分量c的实部和虚部的傅里叶谱及其全矢谱分别如图7、图8所示。

从图7 可知，Re［c1］和Im［c1］的固有特征频率和z的相同；而c2和c3也为调制信号；c4的频谱中主要含有基频X和2倍频（2X）成分，且幅值与z中的基频量和2倍频分量大致相等。结合图5、图6中c4的平面图，可将c4看作轴心运动轨迹，并且从c4的三维图中可知轴心轨迹的运动方向。图7中各旋转分量实部的振动幅值大于虚部，频谱出现了差异性，而且实部和虚部的频谱仅反映故障信号在某一个方向的振动特征。

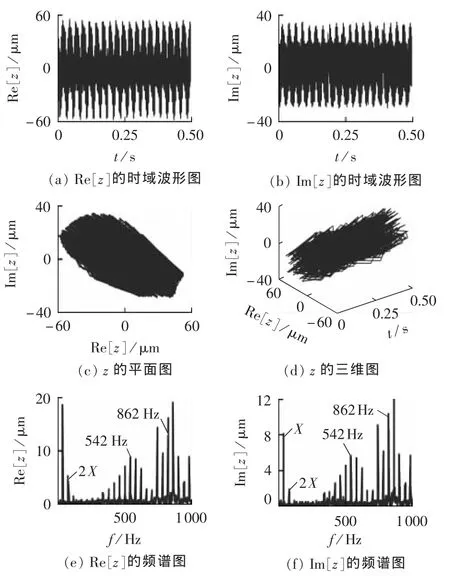
图4 复信号z及其频谱图Fig.4 Complex signal z and its spectrum

图5 对z进行BEMD得到的旋转分量cFig.5 Rotating component c obtained by BEMD of z

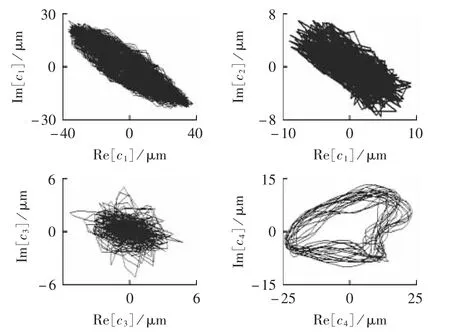
图6 c的平面图Fig.6 Plane diagram of c

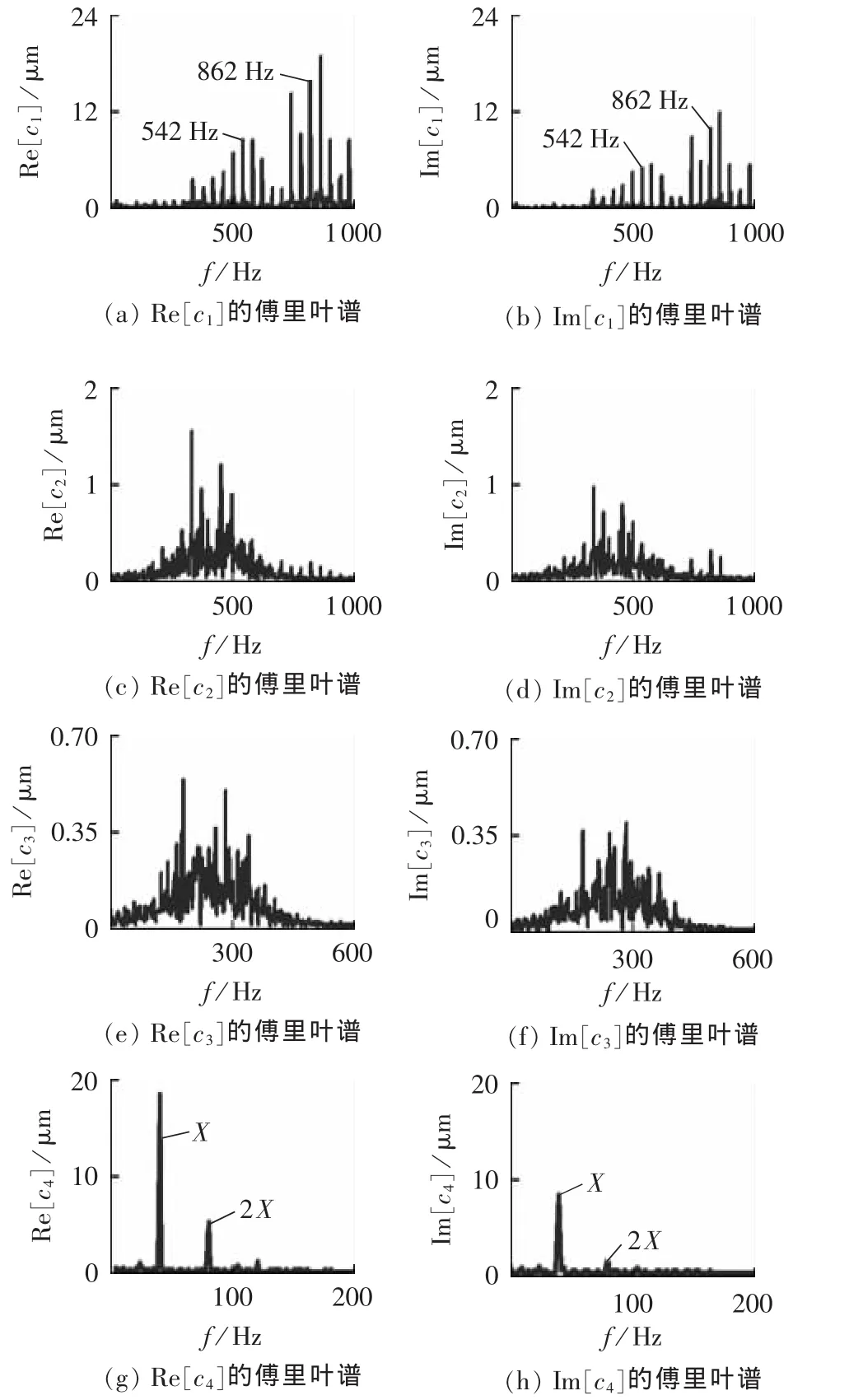
图7 旋转分量实部和虚部的傅里叶谱Fig.7 Fourier spectrums of real and imaginary parts of rotary components

对比图7和图8可知，全矢谱融合了实部信号和虚部信号的振动特征，真实反映了转子在同一截面的振动特征，其振动强度要高于任一方向振动信号的振动强度，频谱结构更为清晰，且结果具有唯一性。

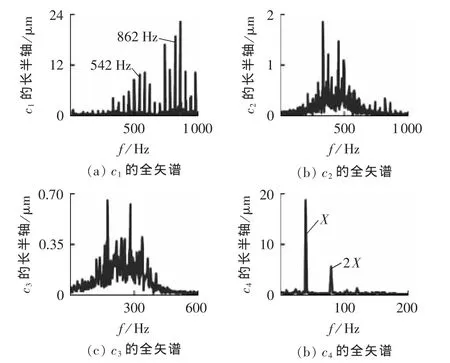
图8 各旋转分量的全矢谱Fig.8 Full vector spectrums of rotational components

另外，图7和图8中c1、c2、c3含有大量的边频带，可知c1、c2、c3属于调制信号，解调可有效获取调制信号中的故障特征，本文运用2.2节提出的基于BEMD和HT的全矢包络谱方法提取调制信号的特征信息。c的实部和虚部的包络谱、全矢包络谱分别如图9、图10所示。图9 中，Re［c1］和Im［c1］包络谱含有X—14X成分，Re［c1］包络谱的振动幅值大于Im［c1］包络谱的振动幅值，频谱幅值出现了差异性；图10中与c1对应的第1阶全矢包络谱也含X—14X成分，且振动幅值高于任一方向振动信号的振动幅值。图9中 Re［c2］和Im［c2］的包络谱主要含有 X和3X成分，2X成分较小；图10中与c2对应的第2阶全矢包络谱除X和3X成分的幅值大于Re［c2］和Im［c2］的外，2X成分较为清晰。图9中Re［c3］的包络谱主要含有2X成分，而Im［c3］的包络谱除2X成分外，还有较多的X成分，此时，二者的频谱结构出现了明显的差异性；图10中的第3阶全矢包络谱有效融合了 Re［c3］和Im［c3］的包络信息，频谱结构更为清晰、全面。图9中Re［c4］的包络谱主要含有X和2X成分，而Im［c4］的包络谱中仅有X成分，二者频谱结构也出现了差异性；而图10中与c4对应的第4阶全矢包络谱含有 X和2X 成分，融合了 Re［c4］和Im［c4］的包络信息。由全矢包络谱可知转子发生了碰摩故障。

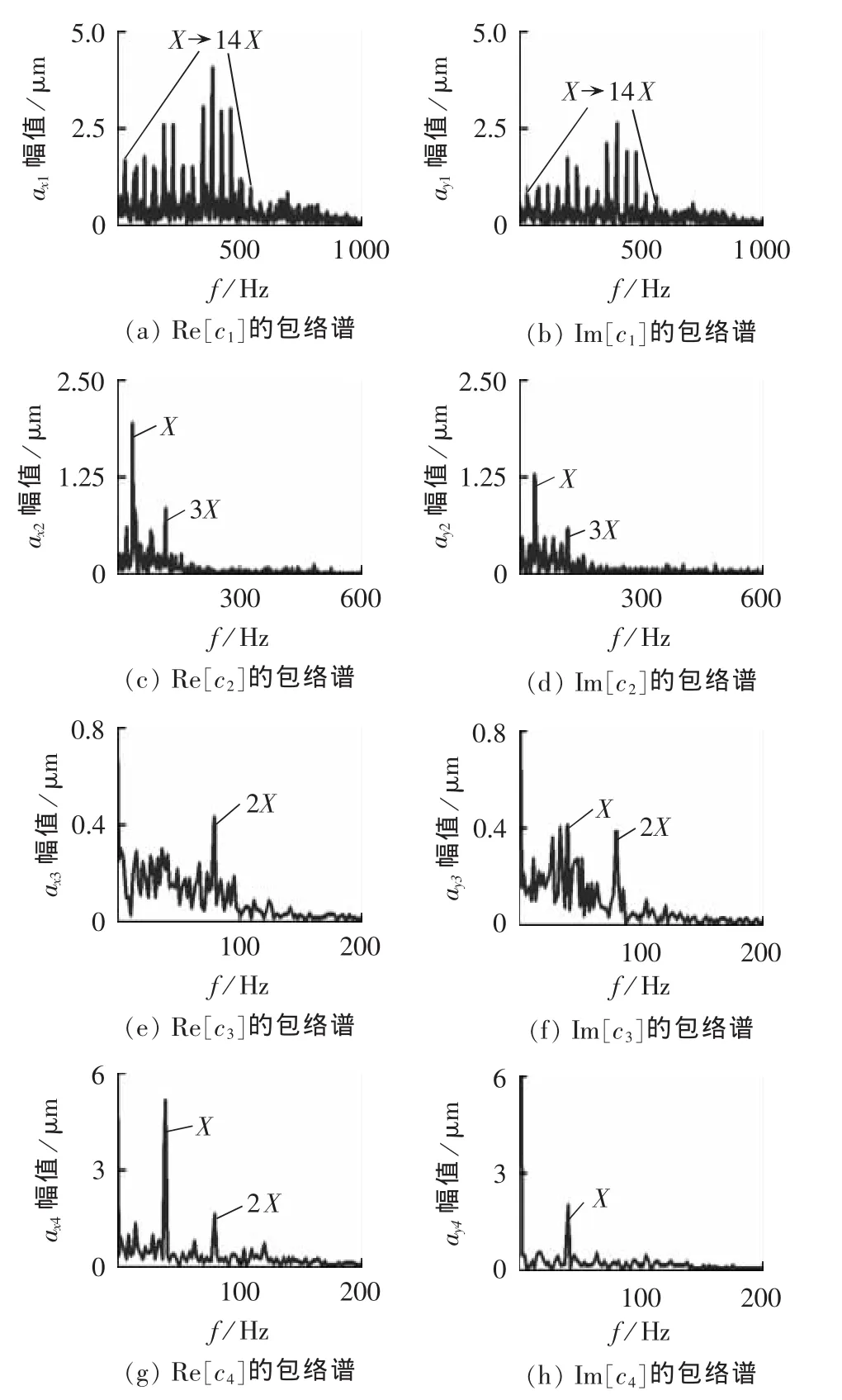
图9 旋转分量c的实部和虚部信号的包络谱Fig.9 Envelope spectrums of real and imaginary parts of rotary components

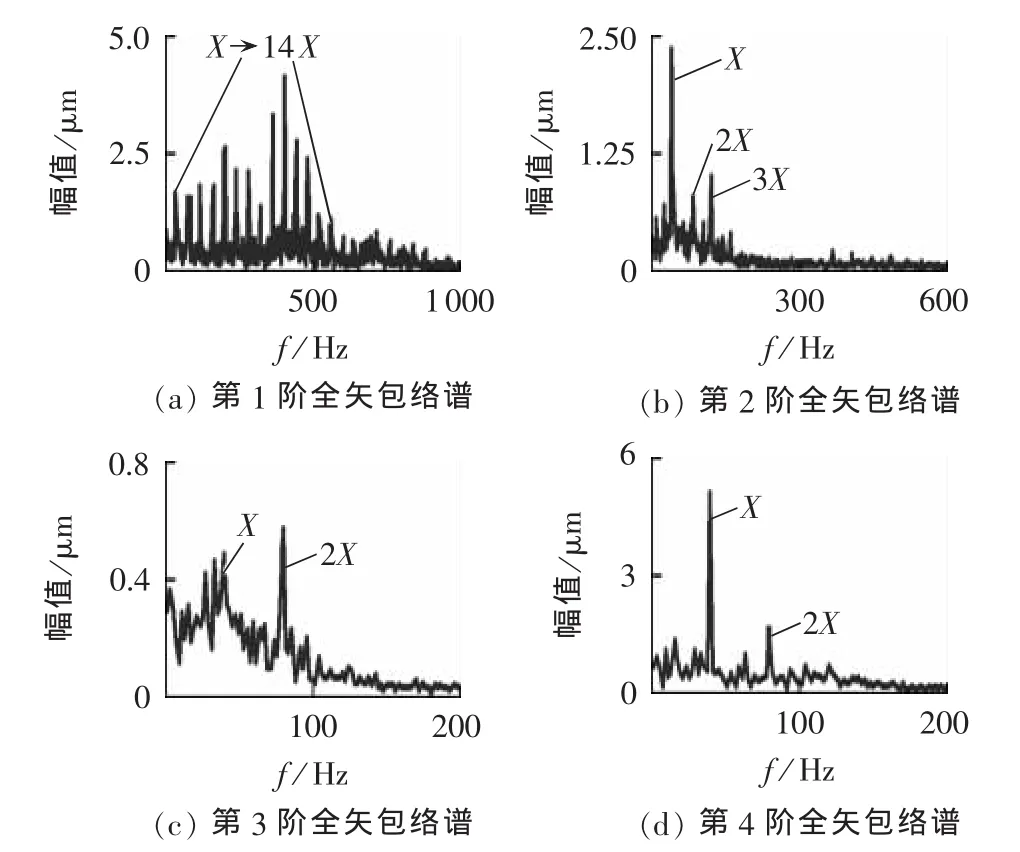
图10 旋转分量c的全矢包络谱Fig.10 Full vector envelope spectrums of rotary components

3.2 TRT振动故障信号分析

某钢铁公司1号TRT发电机组的额定转速为3000 r/min，额定功率为3000 kW，均为滑动轴承支承、圆柱瓦结构。透平转子自由端由于密封不好，出现部分漏气现象；发电机靠近透平转子端径向跳动非常强烈，无法连续运行，且不定期出现跳车事故。根据该机组特点，提取轴承座处壳体振动信号，测点布置见图11，共设置3个测点（进气端由于漏气没有布置测点），8个振动通道，其中6个径向通道和2个轴向通道；采样频率为1600 Hz，采样点数为1024。

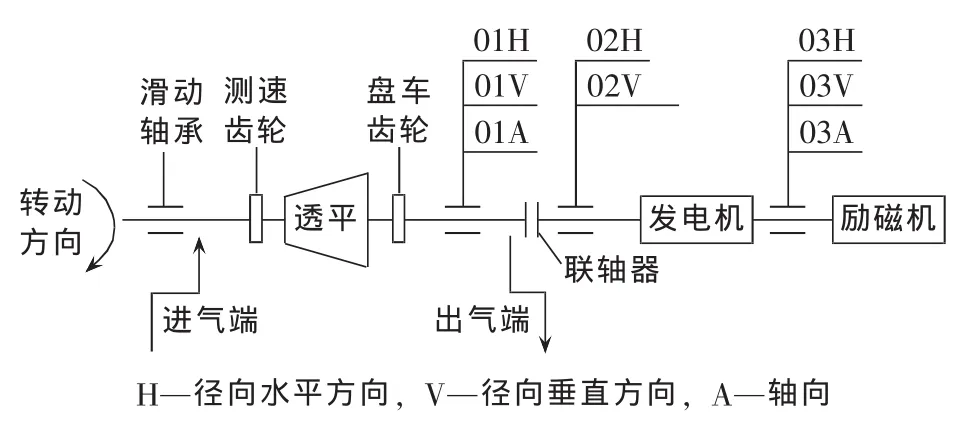
图11 TRT机组结构和测点布置图Fig.11 Structure and measuring point arrangement of TRT unit

在测点2采集的径向通道的水平方向信号x、垂直方向信号y及其傅里叶谱和复信号z（z=x+jy）如图12所示。

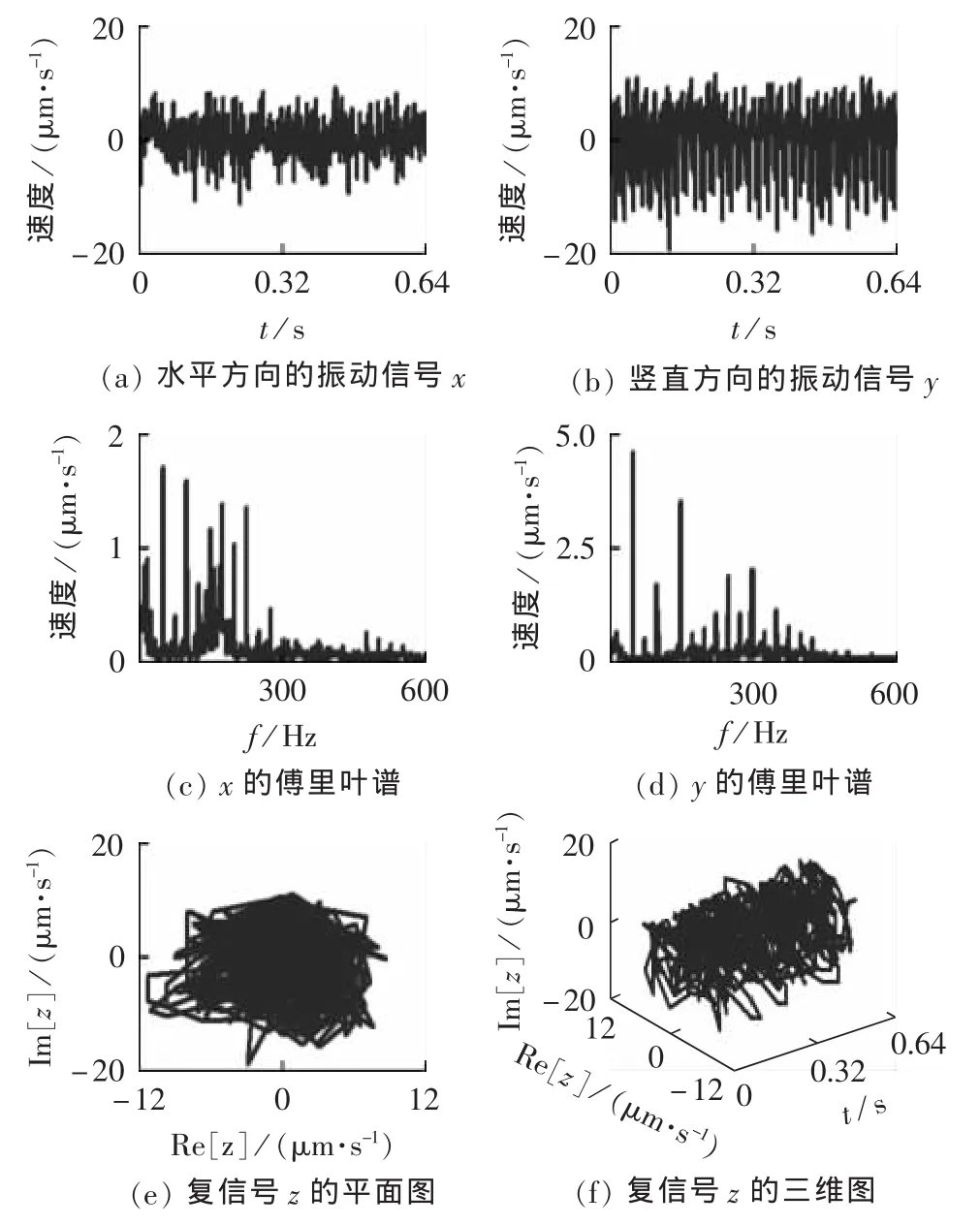
图12 信号x、y及其傅里叶谱和复数信号zFig.12 Signal x and y and their Fourier spectrums，and complex signal z

由图12（c）、（d）可知 x和y 的频谱结构差异较大，x的频谱结构中存在较大的X和2X成分，X成分的幅值最大，2X成分的幅值与X成分的幅值相差不大；另外，还有X/2和X/3分频成分，而且x的频谱结构中存在固有频率为175 Hz的边频带，间隔为25 Hz，固有振动频率幅值与X和2X成分的幅值较为接近。y的频谱中有X、2X和3X成分，其中X成分的幅值最大，3X成分的幅值次之，2X成分的幅值最小；另外，y的频谱中存在固有频率为300 Hz的边频带，间隔为25 Hz，相较于X成分，固有振动频率的幅值较小。通过z的平面图和三维图可知，轴心轨迹比较凌乱，不再是一个椭圆。

由于x和y的频谱中都存在边频带，而且频谱结构差异较大，为使分析结果具有唯一性，避免出现漏判或误判，本文采用2.2节中提出的二元全矢包络谱技术对复信号z进行分析。运用BEMD将z分解成 c1—c4和r，如图13所示，从图中可知 c1、c2和c3的运动轨迹比较凌乱，含有故障特征信息，而c4的运动轨迹为一个椭圆，可认为是提纯的轴心运动轨迹。另外，在c1—c4的傅里叶谱中c1、c2和c3存在边频带，而c4只含有X和2X成分（限于篇幅，未给出它们的傅里叶谱和全矢谱）。

图13 对z进行BEMD获得的系列旋转分量Fig.13 Series of rotating components c obtained by BEMD of z

c1、c2、c3实部和虚部的包络谱如图14所示，与其对应的全矢包络谱如图15所示。图14中，Re［c1］的包络谱的X/2成分和X成分的幅值都较大，1.5X和2X成分的幅值都较小。由于含有幅值较大的X/2成分，从Re［c1］的包络谱可知发生了摩擦；Im［c1］的包络谱中X成分的幅值最大，2X成分次之，1.5X 成分最小；与 Re［c1］相比，Im［c1］的包络谱幅值较大，仅从Im［c1］包络谱可知发生了碰摩。图15中的第1阶全矢包络谱含有X/2、X、1.5X和2X成分，X成分的幅值最大，2X成分的幅值次之，X/2成分的幅值最小，显而易见，第1阶全矢包络谱有效融合了 Re［c1］和Im［c1］的包络特征。由于 2X 成分的幅值较大，从第1阶全矢包络谱谱可知故障以碰摩为主。

图14 前3阶旋转分量的包络谱Fig.14 Envelope spectrums of first three order rotation components

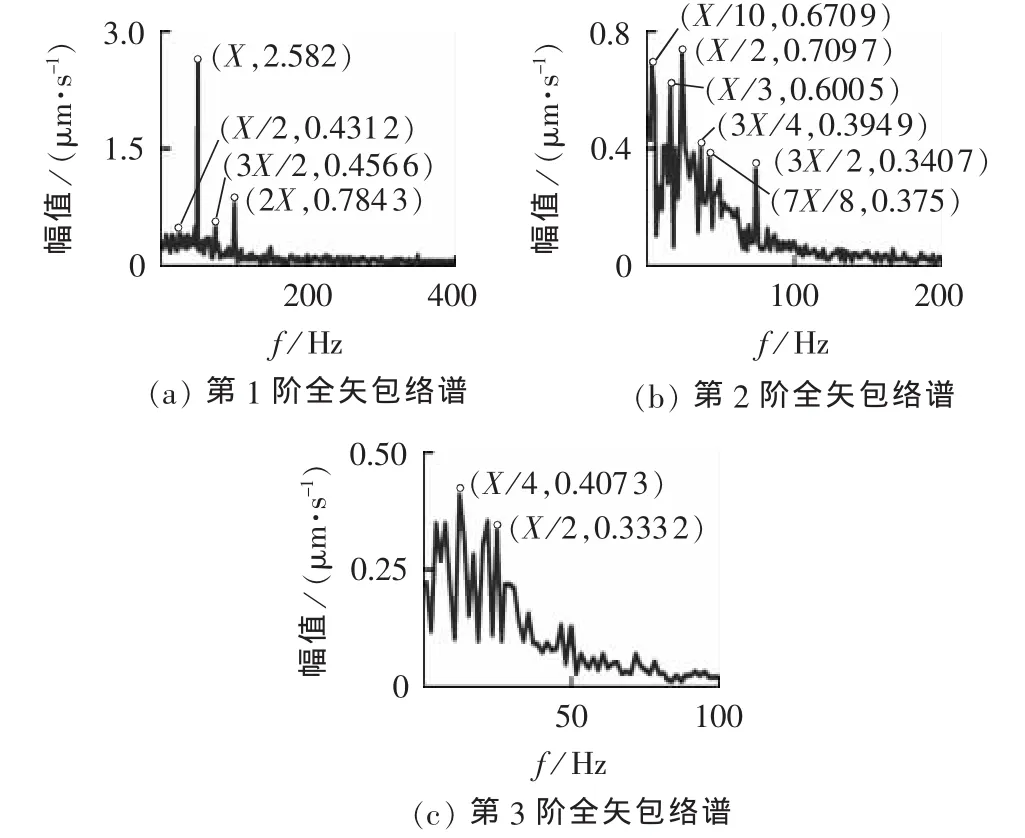
图15 前3阶分量的全矢包络谱Fig.15 Full vector envelope spectrums of first three order rotation components

图14 中 Re［c2］包络谱中 X/10、X/3、X/2、7X/8、X和3X/2成分按幅值依次减小的顺序排列，其中X/10、X/3 成分强度较大；图14 中 Im［c2］包络谱有X/2、X/10、3X/4和3X/2 特征频率。很明显，c2的实部和虚部信号的包络谱差异较大，仅根据单一方向的信号特征进行故障诊断会出现漏判或误判。而第2阶全矢包络谱有效融合了c2实部和虚部的包络谱特征，含有 X/10、X/3、X/2、3X /4、7X/8和3X/2 成分谱线，而且X/2成分的幅值最大、X/10和X/3成分的幅值次之，由此可知发生了油膜涡动和轴瓦摩擦故障。显然，根据第2阶全矢包络谱进行的诊断结果更为全面和准确，避免了漏判以及误判。图14中Re［c3］的包络谱中，X/2 成分的谱线最明显，Im［c3］的包络谱中，X/4成分的谱线最强。图15中与之对应的第 3 阶包络谱也有效融合了 Re［c3］和Im［c3］的包络特征，含有X/4和X/2成分，并且X/4成分的谱线幅值最大，可知轴瓦发生了摩擦。

综合第1—3阶全矢包络谱可知，滑动轴承发生了碰摩故障和摩擦故障。拆卸发电机靠近透平转子端的滑动轴承（测点2），现场故障图如图16所示，可以发现有明显的摩擦和碰摩痕迹，直接证明了本文所提方法的可行性和有效性。

图16 TRT现场故障图Fig.16 Field fault diagram of TRT

4 结论

本文首次将BEMD引入旋转机械故障诊断领域，提出基于二元信号处理技术的BEMD全矢包络谱分析方法，将同源信息融合技术扩展到二元空间。研究中的主要结论如下。

a.BEMD可将复数形式的旋转的振动信号自适应地分解为系列复数形式旋转分量之和。

b.通过BEMD分解复数形式的旋转信号可获取转子的轴心轨迹。

c.TRT的滑动轴承发生摩擦和碰摩时，其径向水平与垂直方向上的振动信号包络谱差异较大。因此，分析不同方向信号的包络谱得到不同的诊断结果，容易造成误判、漏判。

d.实际案例分析结果表明基于BEMD的全矢包络技术可有效融合TRT同一截面2个互相垂直的信号的包络特征，基于BEMD的全矢包络谱可全面反映故障特征，通过全矢包络谱进行故障诊断更全面、准确。

BEMD可以同时处理2个互相垂直的通道的振动信号，将机械故障诊断上升到二元领域进行，非常适合与基于同源信息的故障诊断方法相结合，BEMD在旋转机电设备故障诊断中将有广泛的应用。

参考文献：

［1］马辉，太兴宇，闻邦椿，等.柔性转子系统轮盘外缘定点碰摩动力学特性分析［J］.中国电机工程学报，2012，32（17）：89-96.MA Hui，TAI Xingyu，WEN Bangchun，et al.Dynamic characteristic analysis of a flexible rotor system with fixed-point rubbing fault at a wheel edge［J］.Proceedings of the CSEE，2012，32（17）：89-96.

［2］唐贵基，向玲，朱永利.基于HHT的旋转机械油膜涡动和油膜振荡故障特征分析［J］.中国电机工程学报，2008，28（2）：77-82.TANG Guiji，XIANG Ling，ZHU Yongli.Fault analysis of oil whirl and oil whip based on Hilbert-Huang transform for rotor system［J］.Proceedings of the CSEE，2008，28（2）：77-82.

［3］范炜，刘晓光.基于PC104的风电机组状态监测系统设计［J］.电力自动化设备，2011，31（12）：106-109，123.FAN Wei，LIU Xiaoguang.Design of PC104-based wind turbine state monitoring system［J］.Electric Power Automation Equipment，2011，31（12）：106-109，123.

［4］王国彪，何正嘉，陈雪峰，等.机械故障诊断基础研究“何去何从”［J］.机械工程学报，2013，49（1）：63-72.WANG Guobiao，HE Zhengjia，CHEN Xuefeng，et al.Basic research on machinery fault diagnosis-what is the prescription［J］.Journal of Mechanical Engineering，2013，49（1）：63-72.

［5］陆琳，崔艳华.基于振动信号的变压器分接开关触头故障诊断［J］.电力自动化设备，2012，32（1）：93-97.LU Lin，CUI Yanhua.Diagnosis of transformer tap changer contact fault based on vibration signal［J］.Electric Power Automation Equipment，2012，32（1）：93-97.

［6］张进，冯志鹏，卢文秀，等.交叉小波变换在水轮机非平稳信号分析中的应用［J］.中国电机工程学报，2010，30（23）：84-89.ZHANG Jin，FENG Zhipeng，LU Wenxiu，et al.Application of cross-wavelet transform to hydraulic turbine nonstationary signal analysis［J］.Proceedings of the CSEE，2010，30（23）：84-89.

［7］安学利，蒋东翔，陈杰，等.基于ITD和LS-SVM的风力发电机组轴承故障诊断［J］.电力自动化设备，2011，31（9）：10-13.AN Xueli，JIANG Dongxiang，CHEN Jie，et al.Bearing fault diagnosis based on ITD and LS-SVM for wind turbine［J］.Electric Power Automation Equipment，2011，31（9）：10-13.

［8］秦娜，金炜东，黄进，等.基于EEMD样本熵的高速列车转向架故障特征提取［J］.西南交通大学学报，2014，49（1）：27-32.QIN Na，JIN Weidong，HUANG Jin，et al.Feature extraction of high speed train bogie based on ensemble empirical mode decomposition and sample entropy［J］.Journal of Southwest Jiaotong University，2014，49（1）：27-32.

［9］李莉，朱永利，宋亚奇.变压器绕组多故障条件下的振动信号特征提取［J］.电力自动化设备，2014，34（8）：140-146.LI Li，ZHU Yongli，SONG Yaqi.Feature extraction for vibration signal of transformer winding［J］.Electric Power Automation Equipment，2014，34（8）：140-146.

［10］CHENG Junsheng，YANG Yi，YANG Yu.A rotating machinery fault diagnosis method based on local mean decomposition ［J］.Digital Signal Processing，2011（9）：1-11.

［11］赵洪山，郭伟，邵玲，等.基于子空间方法的风机齿轮箱故障预测算法［J］.电力自动化设备，2015，35（3）：27-32.ZHAO Hongshan，GUO Wei，SHAO Ling，et al.Gearbox fault prediction algorithm based on subspace method for wind turbine［J］.Electric Power Automation Equipment，2015，35（3）：27-32.

［12］马辉，张志，闻邦椿，等.不同载荷下基座松动转子系统动力学特性分析［J］.中国电机工程学报，2012，32（26）：132-137.MA Hui，ZHANG Zhi，WEN Bangchun，et al.Dynamic characteristic analysis of a rotor system with pedestal looseness under two load cases［J］.Proceedings of the CSEE，2012，32（26）：132-137.

［13］韩捷，石来德.全矢谱技术及工程应用［M］.北京：机械工业出版社，2008：56-57.

［14］巩晓赟，韩捷，陈宏，等.全矢小波包-包络分析方法及其在齿轮故障诊断中的应用［J］.振动与冲击，2012，31（12）：92-95.GONG Xiaoyun，HAN Jie，CHEN Hong，et al.Application of full vector wavelet packet and envelope analysis method in gear fault diagnosis［J］.Journal of Vibration and Shock，2012，31（12）：92-95.

［15］陈超，孟雅俊，杜云龙，等.EMD全矢谱技术及其在滑动轴承故障诊断中的应用［J］.机械强度，2015，37（5）：806-811.CHEN Chao，MENG Yajun，DU Yunlong，et al.Application of the full vetor spectrum based on EMD in fault diagosis of bearings［J］.Journal of Mechanical Strength，2015，37（5）：806-811.

［16］黄传金，邬向伟，曹文思.基于LMD的全矢包络技术及其在TRT 振动故障诊断中的应用［J］.电力自动化设备，2015，35（2）：168-174.HUANG Chuanjin，WU Xiangwei，CAO Wensi，et al.Full vector envelope technique and its application in TRT vibration fault diagnosis［J］.Electric Power Automation Equipment，2015，35（2）：168-174.

［17］RILLING G，FLANDRIN P，GONÇALVES P，et al.Bivariate empirical mode decomposition［J］.IEEE Signal Process，2007，Lett.14（12）：936-939.

［18］张维光，韩军，周翔.线结构光多分辨率测量系统数据拼接方法［J］.仪器仪表学报，2013，34（7）：1441-1447.ZHANG Weiguang，HAN Jun，ZHOU Xiang.Data registration method for multiresolution measurement system with line structured light［J］.Chinese Journal of Scientific Instrument，2013，34（7）：1441-1447.