用运动分解解决带电粒子在复合场中的运动问题
2018-05-18王晓宁
王晓宁
(南宫中学 河北 邢台 055750)
带电粒子在复合场中的运动常见类型:电场力、洛伦兹力、重力三者平衡,做匀速直线运动;或是电场力、重力平衡,在洛伦兹力的作用下做匀速圆周运动.但如果不是这样完美、熟悉的规律,我们在高中阶段又如何将复杂的运动,化解为熟悉的运动规律呢?我们可以用运动的分解解决一类带电粒子在复合场中的运动问题.
我们以一道例题为例.
【例1】如图1所示,空间存在着匀强电场E和匀强磁场B,匀强电场E沿y轴正方向,匀强磁场B沿z轴正方向.质量为m,电荷量为+q的带电粒子,t=0时刻在原点O,以沿x轴正方向的速度v0射入.粒子所受重力忽略不计.关于粒子在任意时刻t的速度沿x轴和y轴方向的分量vx和vy,请通过合理的分析,判断下列选项中可能正确的是

图1 例1题图
解法一:本题中粒子所受的电场力与洛伦兹力不一定平衡,问题描述的情景非常复杂,速度的表达形式也非常复杂,作为一个选择题,当然可以用选择题的解法——特殊值法.
初始时刻,粒子速度为v0,即
vx=v0vy=0
由数学知识
sinθ=0 cosθ=1
将t=0代入选项立即可得选择B对学生而言,没任何问题,可以认为是特殊值方法的一个绝佳运用.
对教师而言,能否得出题目的详细的解答过程呢?
解法二:我们在学习曲线运动时有一个基本的方法——运动的分解:我们可以将初速度v0分解,将其看成水平向右的两个速度的合成:其中一个速度v1满足洛伦兹力和电场力平衡

图2 速度分解
这样粒子的复杂的圆周运动就可以等效为沿x方向的匀速直线运动和一个匀速圆周运动的合成对于圆周运动而言,经过时间t,转过的角度满足
这样我们通过速度的分解,完美解决了这个复杂的曲线运动问题.
任意时刻的速度为
知道了粒子的速度情况,我们也可以得出粒子运动方程.
设粒子做匀速圆周运动的半径为R,有
则粒子的运动方程为
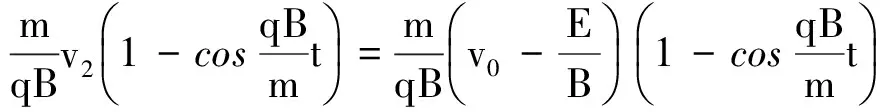
上述以时间t为参数的方程表明,粒子的运动轨迹为摆线.
另外,我们对运动过程用动能定理
得
将上述y的表达式代入
与利用速度的分解得出的结果是一致的,用运动分解的思路没问题.
由此我们想到如果粒子由静止释放,是不是也能这样处理呢?
我们可以“无中生有”,给带电粒子配上一对等大反向的速度.
如图2所示,若电荷量为+q的粒子从复合场中的O点有静止释放(重力不计),我们可以认为此时粒子是水平向右的速度v0和水平向左的速度v0的合成,其中向右的速度v0恰好满足qv0B=qE,这样电场力被抵消,粒子的运动可以看成以-v0为初速度的匀速圆周运动和以v0向右的匀速直线运动的合成粒子在任意时刻的位移
粒子在任意时刻的分速度
其合速度大小
从上式可以得到,当粒子运动到最低点时
速度最大为
这个结果也可以由速度的合成得到,当粒子运动到最低点时,圆周运动的速度方向与直线运动的速度方向一致,两个分速度等大同向.
有了这个知识,再看2008年江苏高考物理14题.
【例2】在场强为B的水平匀强磁场中,一质量为m,带正电q的小球在O静止释放,小球的运动曲线如图3所示.已知此曲线在最低点的曲率半径为该点到x轴距离的2倍,重力加速度为g.求:
(1)小球运动到任意位置P(x,y)的速率v;
(2)小球在运动过程中第一次下降的最大距离ym;

图3 例2题图
第(2)、(3)问中,题目所给条件“曲线在最低点的曲率半径为该点到x轴距离的2倍”就是多余的.
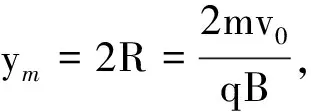
(3)设想小球具有-v1和v1的初速度,其中v1对应的洛伦兹力沿+y方向,满足
mg+qv1B=qB
小球以-v1沿-x方向做匀速直线运动,同时以v1为初速度做逆时针的匀速圆周运动,最大速率时,圆周运动的速度方向与直线运动的速度方向一致.
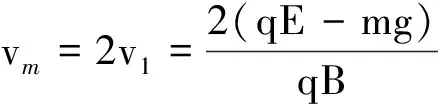
这类复杂的曲线运动,我们等效为沿某一方向的匀速直线运动和一个匀速圆周运动的合成,借助等效原理和运动的分解原理,在全新的数理模型基础上,简化了问题,使之得到了较好的解决.
