用“好”素材 促“真”理解
——以“确定位置”的教学为例
2018-05-18福建晋江市实验小学362200颜乙红
福建晋江市实验小学(362200) 颜乙红
【教学内容】
北师大版教材四年级上册第五单元第二课时“确定位置”
【课前慎思】
“确定位置”就是刻画物体或图形位置的方式——用有序数对(a,b)表示物体(点)在平面中的位置。其实质是“在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序数对与它对应,反过来,对于任意一个有序对,都有平面上唯一的一点与它对应”。这个知识点与其他知识点最大的不同在于它的本源是数学而不是生活,但又可依附于现实结构,因此教材从学生的座位“某组某排”引入确定位置。通过课前问卷调查发现,98%的学生自习课本就能依样画葫芦用两个数来表示位置,但对于“为什么要用数学语言来刻画一个点的位置?如何刻画?刻画的价值在哪里?”则很茫然。其实从数学史的角度来看,笛卡尔发明坐标的用意是用它来解决几何计算问题;从学生的认知来看,学生早在一年级时便有了在一维中刻画位置的经验(如前后、上下、左右),在二维中刻画位置的经验(如东南西北)。本课是在二维中正式学习如何用两个数表达点的位置,而确定点的位置,就是确定好点的横向位置和纵向位置,不管是行还是列、组还是排,都是生活语言表达的需要。在明确用数对确定位置的内涵及教育价值后,就可以“用‘好”素材,促‘真’理解”为指导思想设计教学。
【教学实践】
一、用“好”故事素材,从知识源头出发
师:今天有一只蜘蛛要和我们一起上课。瞧,它来了。蜘蛛在哪里?它悄悄地爬上横梁躲在某个灯笼后面。猜猜它在里?(课件出示图1)
图1
(学生随意猜测)
师:给你们一点提示。(课件出示数字“2”)现在你觉得它在哪里?
生1:可能是从左边数起第二个。
生2:可能是从右边数起第二个。
师:到底是从右边数起,还是从左边数起呢?能确定么?
生(齐):不能。
师:想一想,还要再提供什么信息才能确定蜘蛛的位置?(板书:确定位置)
生3:还要说是从左边数起还是从右边数起。
师:也就是还要提供数的———
生(齐):方向。
师:再给你们一点提示(板书:→)。现在你能确定蜘蛛的位置了么?
生4:知道了,蜘蛛就藏在从左边数起的第二个灯笼里。
师:你们真不简单,给个方向和数字就马上猜中了。这里有这么多灯笼,如果想让人一眼看出每个灯笼对应是第几个。怎么办?
生5:标数字。
师:我们试着在对应灯笼的下面标上数字。(课件出示:在对应灯笼下标数字)
师(手指横梁的起点):这个地方标多少呢?
生6:0。因为0表示起点。
师:能用一个数表示蜘蛛现在的位置么?
生7:2 。
师:2表示什么意思?
生7:第2个灯笼的地方。
师:也就说灯笼的顺序是2。
师:如果从起点开始一段一段地数,2还可以表示什么?
生8:距离起点2个间断的地方。
师:2还能表示和起点的距离。
师:蜘蛛趴在这里好一会儿了,它想换个位置了,于是又继续爬。(课件分别演示蜘蛛爬到第三、四、五个灯笼后面)现在的位置是——
生:3;4;5。
师:只要蜘蛛继续在横梁上爬,我们就可以用——
生9:一个数确定它的位置。
【设计意图:把握用数对确定位置的数学本质,以数学家笛卡尔用数对确定点的位置的素材为切入点,从方法源头——一维空间出发,创设“蜘蛛在哪里”的问题情境,先让学生观察蜘蛛在横梁上的位置,体会参照物(起点)、方向、距离在确定位置中的重要作用,唤醒学生用一个数确定点在一组线上的位置的经验。】
二、用“好”简单素材,依知识本质建构
1.制造冲突
师:蜘蛛趴在横梁上太久了。它说:“外面的世界那么大,我要去看看。”它又继续爬了。(课件出示蜘蛛从第3个灯笼往上爬)什么变了?
生1:位置变了,爬的方向也变了。刚才是从左往右爬,现在是从下往上爬。(板书↑)
师:现在蜘蛛爬到哪里了?
生2:3 的上面。
师:如果蜘蛛再往上爬一点呢?
生3:还是3的上面。
师:再往上爬一点呢?
生4:还是3的上面。
师:如果蜘蛛不小心往下掉了一点呢?
生5:也是3的上面。
师:都说是3的上面,这样真的能说清楚蜘蛛的具体位置么?
生6:不能。
师:怎么办?
生7:在左边的柱子上标数字。
师:怎么知道在多高的地方标几?
生8:1段高的地方标1,2段高的地方标2……(学生用手比画起点到第1个灯笼的距离为一段)
师:我跟你们想到一块了。(课件出示:在柱子上挂上灯笼)
师(指着第一个灯笼):这里标多少?
生9:1。
师:课件出示数字:现在能看出蜘蛛往上爬了几段么?
生10:2 段。
【设计意图:制造认知冲突,让学生体会仅仅用一个数已经无法准确表示出蜘蛛的位置,从而深入思考,提出解决问题的办法,这是学生的思维从一维向二维发展的过程。】
2.尝试建构
师:为了便于观察蜘蛛的位置,我们可以把横梁和柱子看成线,灯笼和起点的位置看成点,蜘蛛可以化身为点。老师已经把这只蜘蛛,也就是点变到你们的学习单上去了,请你们拿出学习单1,用自己的方法表示蜘蛛的位置。
生11:蜘蛛的位置是“3上面2段的地方”。3表示从左往右横着数3段,2表示从下往上竖着数2段。
生12:蜘蛛的位置是“横3竖2”。我也是从左往右横着数3段,从下往上竖着数2段。
生13:蜘蛛的位置是“3、2”。
师:这些记录的方法中有什么共同的地方?
生14:都用到了数字3和2。
师:你真善于观察和比较,我要把你的发现记录下来。(板书:3 2)
师:3表示——从左往右横着数3段的位置,表示的是点的横向位置(板书:横向位置)。2表示——从下往上纵着数2段的位置,表示的是点的纵向位置。(板书:纵向位置)蜘蛛在横梁的时候,我们只要用一个数就能确定它的位置,现在为什么要用两个数?
生15:用两个数能更准确地表示蜘蛛的位置。
师:是啊,现在蜘蛛是在一个平面上,它既有——横向位置,又有——纵向位置,所以要用两个数来确定它的位置。你们真是善于总结,数学家笛卡尔可是经过漫长的思考才想到用2个数表示点的位置,而我们只用了短短的十几分钟就做到了。看看数学家笛卡尔是怎么想的。(微课展示笛卡尔创造数对的故事和数对的读、写法)
师:你们跟数学家一样,创造了两个数来确定蜘蛛的位置。数学家规定,先写——(表示横向的位置的数),再写——(表示纵向位置的数),接着——
生16:中间用逗号隔开。
师:是的,用逗号区分横向位置和纵向位置。
生17:外面加括号。
师:没错,用括号表示一个整体。
师:这就是我们今天学习的确定位置的方法——用数对来确定位置。这个数对读作——(数对三二),我们就用(3,2)来表示这个点的位置。
【设计意图:学生自主尝试,创造了表示蜘蛛(点)在平面上的位置的方法,体会到使用两个数在平面上确定点的位置的必要性。用微课的形式呈现笛卡尔用数对表示点的位置的故事,再次巧妙地把数对的意义、读法和写法融入其中。这是数学史和数学文化的延伸,是数学知识与逻辑的进一步抽象和深化,能够促进学生理解规则产生、表达和形成的过程。】
3.深化认知
师:一个点的位置可以用数对表示,如果有很多个点呢?老师把每个点的横向位置和纵向位置用横线和竖线画出来,形成了方格图。现在就在方格图上研究格点的位置。
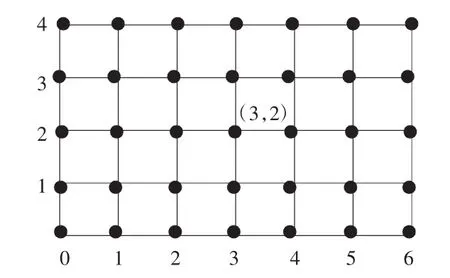
图2
师(把鼠标放在点(4,2)上):怎么用数对表示这个点的位置?这个点能用(2,4)表示么?
生18:不能。
师:怎么不能?还不都是这两个数字?
生19:(2,4)的横向位置是 2,纵向位置是 4,而这个点的横向位置是4,纵向位置是2。
师:你分析得真清楚。那(2,4)表示的点又在哪里?(请学生指出点(2,4)的位置)
师:原来(4,2)和(2,4)表示的位置是不一样的啊。
师:用数对确定位置时应该注意什么?
生20:注意数的顺序。
师:是啊,数对里的这两个数是有序的。(板书:有序)数字的顺序不一样,表示的点的位置就不同。
师:一个数对对应几个点?
生21:1 个点。
师:没错,唯一的一个点。反过来呢,一个点也只对应一个数对。
师:是的,唯一的一个数对。(板书:唯一)
师(出示图3):这里还有两个神秘的点A、B,你能用数对表示它们的位置么?
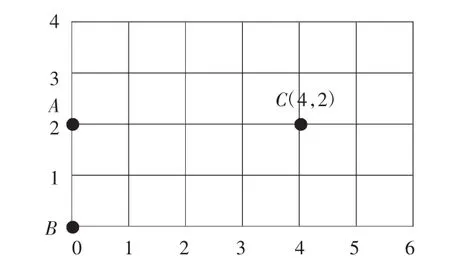
图3
生22:A 点是(0,2),B 点是(0,0)
师:依次连接A、B、C,得到一个什么图形?
生23:三角形。
师:是的,确定了这三个点的位置,三角形的形状和大小也就确定了。
师(课件出示三角形向右平3格):三角形怎么了?

图4
生24:平移后位置变了。
师:请用数对说说点的位置是怎么变的。
生25:原来 A点的位置是(0,2),现在是(3,2)。
生26:原来 B 点的位置是(0,0),现在是(3,0)。
生27:原来 C 点的位置是(4,2),现在是(7,2)。
师:真厉害,C点在格子外你都能看出来。怎么确定生27说的对不对?
生28:延长横线和竖线,扩充格子图。
师:听你们的。(课件演示扩充格子图)C点果然是(7,2)。
师(课件演示图形旋转):三角形又怎么了?请用数对说说位置是怎么变的。

图5
生29:原来 A点的位置是(3,2),现在是(1,0)。
……
师:正如著名数学家华罗庚所说,“数形结合百般好,隔离分家万事休。”我们以后还将通过研究数的规律来了解图形的特征。
【设计意图:由表示一点的位置到表示多点的位置,学生深刻体会到每个点都有一个横向的位置和一个纵向位置,把两个方向线标出来,便形成了方格图,每个交叉点的位置可以用两个数(数对)来表示。通过用点的位置描述图形的位置变化,渗透了一一对应、数形结合等数学思想,发展了学生的空间观念。】
三、用好生活素材,就知识的应用拓展
师:刚才我们用数对确定蜘蛛的位置也就是点的位置。你们在教室里也有自己的位置,比如说第一组、第二组、第三组,我们把这样的排列称为组,我们班一总共有八组;还有第一排、第二排、第三排,我们班一总共有八排。老师要把你们的位置搬到屏幕上来。看——这是咱们班的座位分布图(课件出示班级座位图)。请你对照座位图,找找自己的位置。可以把组看成竖线,把排看成横线。横线和竖线的交点对应的就是座位。
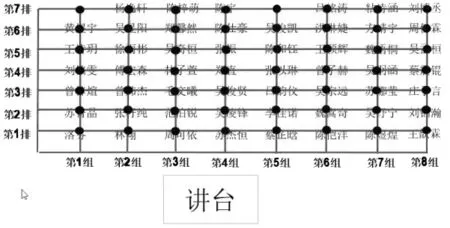
图6
生1:我的座位是(3,5)。
师:真棒。用数对表示位置显得很——
生(齐):简洁。(板书:简洁)
师:你们能用数对简洁地表示自己的位置么?
生2:用数对表示我的位置是(3,2)。
师:刚才那只蜘蛛的位置用(3,2)表示,你的位置也用(3,2)表示,为什么?
生2:因为我的横向位置和纵向位置都和蜘蛛一样。
师:老师要考考你们的反应能力。我报数对,请对应的同学起立。(1,1),(2,2),…,(7,7)。(对应的学生起立,教师在课件上标出数对对应的点)
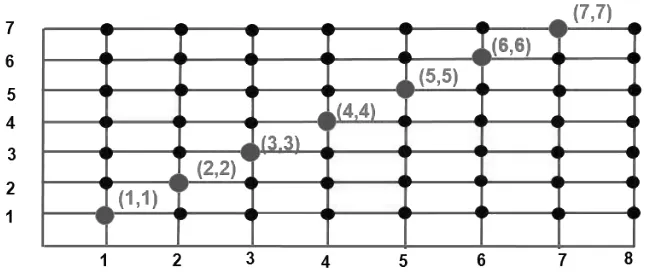
图7
师:老师报的这些数对有没有什么特点?
生3:数对的第一个数和第二个数一样。
生4:横向位置和纵向位置相同。
师:这些数对所对应的点:连起来是一条斜线。
师:真有想象力。我们现在来玩用数对开火车的游戏。请第三组的同学从前往后依次报出表示自己位置的数对。(学生依次报出:(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(3,7)(3,8))
师:这些数对有没有什么特别之处?
生5:同一组的同学,数对的第一个数字一样。
师:同一组的同学在同一纵线上,他们的横向位置一样,所以数对的第一个数一样。想一想,同一排的同学报出的数对又会有什么特点?
生6:数对的第二个数一样。
师:是这样么?我们用事实来说话。请同一排的同学报出数对。(学生依次报出:(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)(7,2)(8,2))
师:果然和预料的结果一样。同一排的同学,他们在同一横线上,纵向位置一样,所以数对的第二个数一样。
师:大家真了不起,都学会了用数对来确定自己的位置。要感谢蜘蛛陪我们上了一节课,让我们像数学家一样经历了数对的产生过程。回头看,当蜘蛛在横梁上,我们用一个数确定蜘蛛的位置;当蜘蛛爬到墙面上,我们用2个数,也就是用数对确定它的位置。现在,蜘蛛要回家了,它离开了墙面挂在了半空中,这时候确定它的位置该用几个数呢?
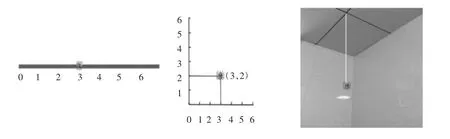
生7:用3个数。因为既要横着数,也要纵着数,还要竖着数。(用手比出了三个方向)
师:这是你们的想法,当蜘蛛变为卫星升上太空,或者化身为核潜艇潜入深海,我们又该怎么确定它的位置?这些问题都等待着你们去探索,去发现!
【设计意图:把学生的座位图抽象为方格图,让学生根据座位图用数对描述自己的位置,从而感悟数学就在身边。最后对所学知识做了一番梳理,从一维、二维到三维,展示了一个较为完整的知识体系,激发学生继续学习的热情。】
