数形结合思想在小学数学中的应用
2018-05-18河北邢台市二十冶综合学校小学一分校054100苏春峰
河北邢台市二十冶综合学校小学一分校(054100) 苏春峰
“数”及“形”是数学内两个最基本概念,数能让形量化,形可使数更为形象。数学教学中数形结合,将数学中数量关系、运算等同图形结合思考,可让数形间优势互补。小学为数学启蒙阶段,将数形结合思想应用到小学数学教学中,能帮助学生顺利构建数学模型,学好数学,提高教学成绩。
一、用直尺感知数形结合
小学生对数列规律难以理解,教学中可以借助学生熟悉的直尺对数列进行讲解。教学中可将直尺当作是“数尺”,也就是可以将抽象的数在熟悉的可以看见的数尺(只有自然数,不存在刻度)上进行有方向、有规律的排列,将抽象数在数尺上直观形象展示,这样不仅可以帮助学生理解数的大小、顺序,还能帮助他们对数列规律简单理解。
二、用线段图理解数量关系
小学生对数量关系难以理解,遇到题目不知道如何入手,而线段图则可以让抽象的数量关系变得形象,易于理解。在遇到“求比一个数的几倍还多几(少几)”这类应用题时,单纯列式计算,学生很容易出现理解错误,但是结合线段图之后,理解就容易多了。
例如,学校给校内班级配备篮球、排球两种体育用品,其中排球个数为6个,篮球个数为排球数量的4倍少两个,求学校配备的篮球有多少个?
学生对于“几倍少几”“几倍多几”这类的题目难以理解,为使学生理解更为容易,教学中可设计如下图形:

□代表排球,△代表篮球,结合图形,让学生对比两者数量关系。面对此图,学生观察中发现△的个数既可以比□3倍多4个,也能够理解成比□的4倍少2个。如此,学生就能够很容易从两个角度对题目进行解答:(1)△的个数比□3倍多4个:6×3+4=22个。(2)△的个数比□的4倍少2个:6×4-2=22个。
通过上面的例子可以看出解题中,线段图能够让“看不见”变得“清晰可见”,通过线段图,学生可以清晰看出两个物体间的数量关系,拓宽解题思路,从而可以将复杂的解题过程变得更为简单,轻松解决问题。
三、用图形解决容斥、行程问题
小学数学教学中,容斥问题、行程问题也是学生容易出错的两类题目,而如果教学中进行数形结合,通过图形去解决问题,问题就会迎刃而解了。
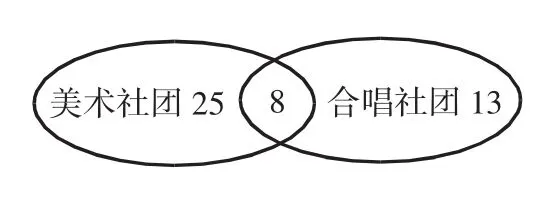
如,五年级三班所有同学都至少参加了一项兴趣社团,其中参加美术社团的有33人,参加合唱社团的有21人,并且有8人两个社团都参加了,问班上的学生人数总共是多少?
解题中可以先画一个如上图所示的图形,从图中能对学生社团参加情况一目了然,能清晰看出8人是重复的那部分,也就可以顺利得出班上学生总人数:33+21-8=47(人)。
行程问题,特别是变速行程问题是小学阶段学生难以理解的一类题目,在没有学习过“二元一次方程”情况下,学生对行程问题中的数量关系用图形进行表示的话就会让题目变得很容易。
如,小张开车从甲地去乙地送货,如果他将车速提高20%的话,可以提前1小时到达;但若是按照原速行驶120km之后,将车速提高25%的话,则可提前40分钟到达目的地。求两地的距离?
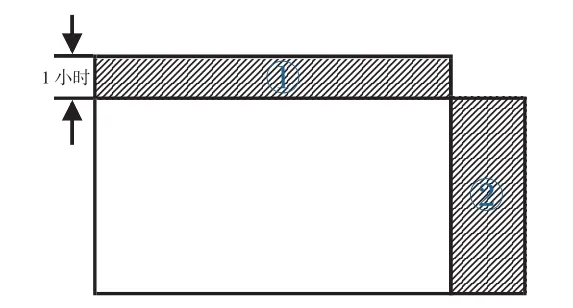
此题可以用长方形面积方法来解决,按照第一种走法,可画出上图,面积代表总路程,长为速度,宽为时间,不论长宽怎样变化,总路程不变,长方形面积相等,则按照这样理解,上图中长方形①的面积等于长方形②的面积,就可以列出:原速度×20%×(原时间-1)=原速度×1,从而求出原时间=6小时。
综上所述,小学数学教学中,应用数形结合思想,能将抽象数学问题进行直观展示,使学生的解题思路更加形象化,进而激发学生的学习兴趣,顺利解决数学问题,使数学教学趣味性更强,让教学达到事半功倍的效果。
